3.6: Sistemas y aplicaciones de segundo orden

Sistemas de Muelles Masivos Sin Amortiguar

Si bien dijimos que normalmente solo miraremos los sistemas de primer orden, a veces es más conveniente estudiar el sistema en la forma en que surge de forma natural. Por ejemplo, supongamos que tenemos 3 masas conectadas por resortes entre dos paredes. Podríamos elegir cualquier número más alto, y las matemáticas serían esencialmente las mismas, pero por simplicidad elegimos 3 ahora mismo. Supongamos también que no hay fricción, es decir, el sistema no está amortiguado. Las masas son\(m_1, m_2\), y\(m_3\) y las constantes de resorte son\(k_1, k_2, k_3\), y\(k_4\). Dejar\(x_1\) ser el desplazamiento desde la posición de reposo de la primera masa,\(x_2\) y\(x_3\) el desplazamiento de la segunda y tercera masa. Haremos, como de costumbre, que los valores positivos salgan a la derecha (a medida\(x_1\) que crece, la primera masa se mueve a la derecha). Ver Figura\(\PageIndex{1}\).

Figura\(\PageIndex{1}\): Sistema de masas y muelles.

Este sencillo sistema aparece en lugares inesperados. Por ejemplo, nuestro mundo realmente consiste en muchas pequeñas partículas de materia que interactúan entre sí. Cuando probamos el sistema anterior con muchas más masas, obtenemos una buena aproximación a cómo se comporta un material elástico. Al tomar de alguna manera un límite del número de masas que van al infinito, obtenemos la ecuación de onda unidimensional continua (que estudiamos en la Sección 4.7). Pero nosotros digremos.

Vamos a configurar las ecuaciones para el sistema de tres masas. Por la ley de Hooke tenemos que la fuerza que actúa sobre la masa es igual a la compresión del resorte multiplicada por la constante del resorte. Por la segunda ley de Newton tenemos que la fuerza es la aceleración por masa. Entonces, si sumamos las fuerzas que actúan sobre cada masa y ponemos el signo correcto frente a cada término, dependiendo de la dirección en la que esté actuando, terminamos con el sistema de ecuaciones deseado.

\[\begin{array}{lll}{m_1 x''_1=-k_1 x_1+k_2(x_2-x_1)}&{\quad}&{=-(k_1+k_2)x_1+k_2x_2,} \\ {m_2x''_2=-k_2(x_2-x_1)+k_3(x_3-x_2)}&{\quad}&{=k_2x_1-(k_2+k_3)x_2+k_3x_3,} \\ {m_3x''_3=-k_3(x_3-x_2)-k_4x_3}&{\quad}&{=k_3x_2-(k_3+k_4)x_3.}\end{array} \nonumber \]

Definimos las matrices

\[ M = \left[ \begin{array}{ccc} m_1 & 0 & 0 \\ 0 & m_2 & 0 \\ 0 & 0 & m_3 \end{array} \right] ~~~{\rm{~and~}}~~~ K= \left[ \begin{array}{ccc} -(k_1+k_2) & k_2 & 0 \\ k_2 & -(k_2+k_3) & k_3 \\ 0 & k_3 & -(k_3+k_4) \end{array} \right]. \nonumber \]

Escribimos la ecuación simplemente como

\[M \vec{x}'' = K \vec{x}. \nonumber \]

En este punto podríamos introducir 3 nuevas variables y escribir un sistema de 6 ecuaciones de primer orden. Afirmamos que esta configuración simple es más fácil de manejar como un sistema de segundo orden. Llamamos\(\vec{x}\) al vector de desplazamiento,\(M\) la matriz de masa y\(K\) la matriz de rigidez.

Ejercicio\(\PageIndex{1}\)

Repita esta configuración para 4 masas (encuentre las matrices\( M\) y\(K\)). Hazlo por 5 masas. ¿Puedes encontrar una receta para hacerlo por\(n\) masas?

Al igual que con una sola ecuación queremos “dividir por”\(M\). Esto significa computar la inversa de\(M\). Las masas son todas distintas de cero y\(M\) es una matriz diagonal, por lo que compaginar la inversa es fácil:

\[ M^{-1}= \left[ \begin{array}{ccc} \frac{1}{m_1} & 0 & 0 \\ 0 & \frac{1}{m_2} & 0 \\ 0 & 0 &\frac{1}{m_3}\end{array} \right]. \nonumber \]

Este hecho sigue fácilmente por cómo multiplicamos las matrices diagonales. Como ejercicio, debes verificar que\(MM^{-1}=M^{-1}M=I.\)

Vamos\(A = M^{-1}K\). Nos fijamos en el sistema\( \vec{x}'' = M^{-1} K \vec{x}\), o

\[ \vec{x}'' = A \vec{x}. \nonumber \]

Muchos sistemas del mundo real pueden ser modelados por esta ecuación. Por simplicidad, solo hablaremos del problema dado de las masas-y-resortes. Intentamos una solución de la forma

\[ \vec{x} =\vec{v} e^{\alpha t}. \nonumber \]

Calculamos eso para esta conjetura,\( \vec{x}'' =\alpha^2 \vec{v} e^{\alpha t}.\) enchufamos nuestra conjetura en la ecuación y obtenemos

\[ \alpha^2 \vec{v} e^{\alpha t} =A \vec{v} e^{\alpha t}. \nonumber \]

Dividimos por\(e^{\alpha t}\) llegar a\( \alpha^2 \vec{v}=A\vec{v}\). De ahí\(\alpha^2\) que si es un valor propio de\(A\) y\(\vec{v}\) es un vector propio correspondiente, hemos encontrado una solución.

En nuestro ejemplo, y en otras aplicaciones comunes, solo\(A\) tiene valores propios negativos reales (y posiblemente un valor propio cero). Por lo que estudiamos sólo este caso. Cuando un valor propio\(\lambda\) es negativo, significa que\(\alpha^2= \lambda\) es negativo. De ahí que haya algún número real\(\omega\) tal que\(-\omega^2 = \lambda\). Entonces\(\alpha= \pm i \omega\). La solución que supusimos fue

\[ \vec{x}= \vec{v}(\cos(\omega t) +i \sin(\omega t)). \nonumber \]

Al tomar las partes reales e imaginarias (nota que\(\vec{v}\) es real), nos encontramos con eso\(\vec{v}\cos(\omega t)\) y\(\vec{v}\sin(\omega t)\) son soluciones linealmente independientes.

Si un valor propio es cero, resulta que ambos\(\vec{v}\) y\(\vec{v}t\) son soluciones, donde\(\vec{v}\) es un autovector correspondiente al valor propio 0.

Ejercicio\(\PageIndex{2}\)

Mostrar que si\(A\) tiene un valor propio cero y\(\vec{v}\) es un vector propio correspondiente, entonces\(\vec{x}=\vec{v}(a+bt)\) es una solución de\(\vec{x}''=A \vec{x}\) para constantes arbitrarias\(a\) y\(b\).

Teorema\(\PageIndex{1}\)

\(A\)Sea una\(n \times n\) matriz con\(n\) distintos valores propios negativos reales que denotamos por\(-\omega_1^2 > -\omega_2^2> \cdots > -\omega_n^2\), y los vectores propios correspondientes por\(\vec{v}_1, \vec{v}_2, \ldots, \vec{v}_n.\) If\(A\) es invertible (es decir, si\(\omega_1>0\)), entonces

\[ \vec{x}(t)= \sum_{i=1}^{n} \vec{v}_i(a_i \cos (\omega_i t) + b_i \sin (\omega_i t)), \nonumber \]

es la solución general de

\[ \vec{x}''=A \vec{x}, \nonumber \]

para algunas constantes arbitrarias\(a_i\) y\(b_i\). Si\(A\) tiene un valor propio cero, es decir\( \omega_1=0\), y todos los demás valores propios son distintos y negativos, entonces la solución general se puede escribir como

\[ \vec{x}(t)= \vec{v}_1(a_1+b_1 t)+ \sum_{i=2}^{n} \vec{v}_i(a_i \cos (\omega_i t) + b_i \sin (\omega_i t)). \nonumber \]

Utilizamos esta solución y la configuración de la introducción de esta sección incluso cuando faltan algunas de las masas y resortes. Por ejemplo, cuando solo hay 2 masas y solo 2 resortes, simplemente tome solo las ecuaciones para las dos masas y establezca todas las constantes de resorte para los resortes que faltan a cero.

Ejemplo\(\PageIndex{1}\):

Supongamos que tenemos el sistema en la Figura\(\PageIndex{2}\), con\(m_1 = 2, m_2=1, k_1 = 4,\) y\(k_2=2.\)

Figura\(\PageIndex{2}\): Sistema de masas y muelles.

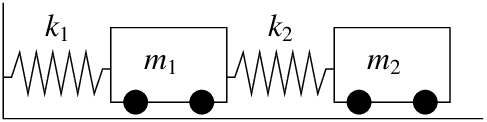
Las ecuaciones que escribimos son

\[ \left[ \begin{array}{cc} 2 & 0 \\ 0 & 1 \end{array} \right] \vec{x}''= \left[ \begin{array}{cc} -(4+2) & 2 \\ 2 & -2 \end{array} \right] \vec{x}, \nonumber \]

o

\[ \vec{x}''= \left[ \begin{array}{cc} -3 & 1 \\ 2 & -2 \end{array} \right] \vec{x}. \nonumber \]

Encontramos los valores propios de\(A\) ser\(\lambda = -1, -4\) (ejercicio). Encontramos vectores propios correspondientes para ser\(\left[ \begin{array}{c} 1 \\ 2 \end{array} \right]\) y\(\left[ \begin{array}{c} 1 \\ -1 \end{array} \right]\) respectivamente (ejercicio).

Comprobamos el teorema y notamos que\(\omega_1=1\) y\(\omega_2=2\). De ahí que la solución general sea

\[ \vec{x}= \left[ \begin{array}{c} 1 \\ 2 \end{array} \right] (a_1 \cos (t) + b_1 \sin (t)) + \left[ \begin{array}{c} 1 \\ -1 \end{array} \right] (a_2 \cos (2t) + b_2 \sin (2t)). \nonumber \]

Los dos términos en la solución representan los dos llamados modos de oscilación natural o normal. Y las dos frecuencias (angulares) son las frecuencias naturales. La primera frecuencia natural es\(1\), y la segunda frecuencia natural es\(2\). Los dos modos están trazados en la Figura\(\PageIndex{3}\).

Figura\(\PageIndex{3}\): Los dos modos del sistema masa-resorte. En la parcela izquierda las masas se mueven al unísono y en la parcela derecha son masas moviéndose en sentido contrario.

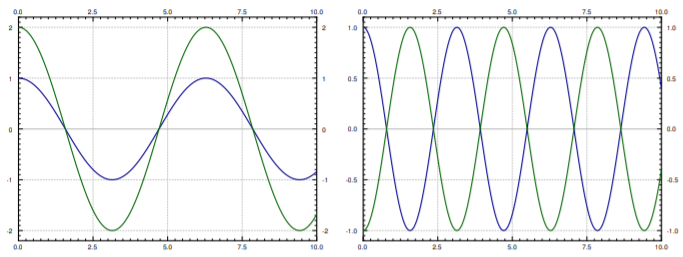
Escribamos la solución como

\[ \vec{x}= \left[ \begin{array}{c} 1 \\ 2 \end{array} \right] c_1 \cos (t-\alpha_1) + \left[ \begin{array}{c} 1 \\ -1 \end{array} \right] c_2 \cos (2t- \alpha_2). \nonumber \]

El primer término,

\[ \left[ \begin{array}{c} 1 \\ 2 \end{array} \right] c_1 \cos (t-\alpha_1) = \left[ \begin{array}{c} c_1 \cos (t-\alpha_1) \\ 2c_1 \cos (t-\alpha_1) \end{array} \right], \nonumber \]

corresponde al modo donde las masas se mueven sincrónicamente en la misma dirección.

El segundo término,

\[ \left[ \begin{array}{c} 1 \\ -1 \end{array} \right] c_2 \cos (2t-\alpha_2) = \left[ \begin{array}{c} c_2 \cos (2t-\alpha_2) \\ -c_2 \cos (2t-\alpha_2) \end{array} \right], \nonumber \]

corresponde al modo donde las masas se mueven sincrónicamente pero en direcciones opuestas.

La solución general es una combinación de los dos modos. Es decir, las condiciones iniciales determinan la amplitud y el desplazamiento de fase de cada modo. Como ejemplo, supongamos que tenemos condiciones iniciales

\[\vec{x}(0) = \begin{bmatrix} 1 \\ -1 \end{bmatrix} , \qquad \vec{x}'(0) = \begin{bmatrix} 0 \\ 6 \end{bmatrix} . \nonumber \]

Utilizamos las\(a_j, b_j\) constantes para resolver las condiciones iniciales. Primero

\[\begin{bmatrix} 1 \\ -1 \end{bmatrix} = \vec{x}(0) = \begin{bmatrix} 1 \\ 2 \end{bmatrix} a_1 + \begin{bmatrix} 1 \\ -1 \end{bmatrix} a_2 = \begin{bmatrix} a_1+a_2 \\2a_1 - a_2 \end{bmatrix} . \nonumber \]

Resolvemos (ejercicio) para encontrar\(a_1 = 0\),\(a_2 = 1\). Para encontrar el\(b_1\) y\(b_2\), diferenciamos primero:\[{\vec{x}}' = \begin{bmatrix} 1 \\ 2 \end{bmatrix} \bigl( - a_1 \sin (t) + b_1 \cos (t) \bigr) + \begin{bmatrix} 1 \\ -1 \end{bmatrix} \bigl( - 2a_2 \sin (2t) + 2 b_2 \cos (2t) \bigr) . \nonumber \]

Ahora resolvemos:\[\begin{bmatrix} 0 \\ 6 \end{bmatrix} = {\vec{x}}'(0) = \begin{bmatrix} 1 \\ 2 \end{bmatrix} b_1 + \begin{bmatrix} 1 \\ -1 \end{bmatrix} 2 b_2 = \begin{bmatrix} b_1+2b_2 \\ 2b_1-2b_2 \end{bmatrix} . \nonumber \]

De nuevo resolver (ejercicio) para encontrar\(b_1 = 2\),\(b_2 = -1\). Entonces nuestra solución es\[\vec{x} = \begin{bmatrix} 1 \\ 2 \end{bmatrix} 2 \sin (t) + \begin{bmatrix} 1 \\ -1 \end{bmatrix} \bigl( \cos (2t) - \sin (2t) \bigr) = \begin{bmatrix} 2 \sin (t) + \cos(2t)- \sin(2t) \\ 4 \sin (t) - \cos(2t) + \sin(2t) \end{bmatrix} . \nonumber \]

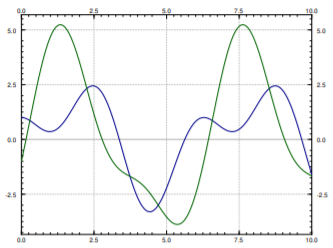
Las gráficas de los dos desplazamientos,\(x_1\) y\(x_2\) de los dos carros se encuentran en la Figura\(\PageIndex{4}\).

Figura\(\PageIndex{4}\): Superposición de los dos modos dadas las condiciones iniciales.

Ejemplo\(\PageIndex{2}\)

Tenemos dos vagones de ferrocarril de juguete. El auto 1 de masa\(2\text{ kg}\) se desplaza\(3\:\frac{\text{m}}{\text{s}}\) hacia el segundo vagón ferroviario de masa\(1\text{ kg}\). Hay un parachoques en el segundo vagón de ferrocarril que engancha en el momento en que los autos chocan (se conecta a dos autos) y no suelta. El parachoques actúa como un resorte de constante de resorte\(k=2\:\frac{\text{N}}{\text{m}}\). El segundo auto está\(10\) a metros de una pared. Ver Figura\(\PageIndex{5}\).

Figura\(\PageIndex{5}\): El choque de dos vagones ferroviarios.

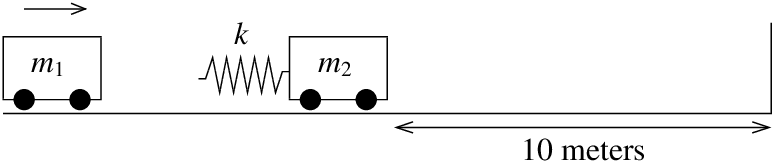
Queremos hacer varias preguntas. ¿A qué hora después del enlace de los autos ocurre el impacto con la pared? ¿Cuál es la velocidad del auto 2 cuando choca contra la pared?

Bien, primero vamos a configurar el sistema. Que\(t=0\) sea el momento en que los dos autos se conecten. Dejar\(x_1\) ser el desplazamiento del primer carro desde la posición en\(t=0\), y dejar\(x_2\) ser el desplazamiento del segundo carro desde su ubicación original. Entonces el momento cuando\(x_2(t)=10\) es exactamente el momento en que se produce el impacto con la pared. Para ello\(t,x'_2(t)\) es la velocidad al impacto. Este sistema actúa igual que el sistema del ejemplo anterior pero sin él\(k_1\). De ahí que la ecuación sea

\[ \left[ \begin{array}{cc} 2 & 0 \\ 0 & 1 \end{array} \right] \vec{x}''= \left[ \begin{array}{cc} -2 & 2 \\ 2 & -2 \end{array} \right] \vec{x}. \nonumber \]

o

\[ \vec{x}''= \left[ \begin{array}{cc} -1 & 1 \\ 2 & -2 \end{array} \right] \vec{x}. \nonumber \]

Calculamos los valores propios de\(A\). No es difícil ver que los valores propios son\(0\) y\(-3\) (ejercicio). Además, los vectores propios son\(\left[ \begin{array}{c} 1 \\ 1 \end{array} \right]\) y\(\left[ \begin{array}{c} 1 \\ -2 \end{array} \right]\) respectivamente (ejercicio). Entonces\(\omega_2= \sqrt{3}\) y por la segunda parte del teorema encontramos nuestra solución general para ser

\[ \begin{align}\begin{aligned} \vec{x}&= \left[ \begin{array}{c} 1 \\ 1 \end{array} \right](a_1+b_1t) + \left[ \begin{array}{c} 1 \\ -2 \end{array} \right](a_2 \cos(\sqrt3 t)+ b_2 \sin(\sqrt3 t)) \\ &=\left[ \begin{array}{c} a_1 + b_1t+a_2 \cos(\sqrt3 t)+ b_2 \sin(\sqrt3 t) \\ a_1+ b_1t- 2a_2 \cos(\sqrt3 t)- 2b_2 \sin(\sqrt3 t) \end{array} \right]\end{aligned}\end{align} \nonumber \]

Ahora aplicamos las condiciones iniciales. Primero los autos arrancan en posición\(0\) así\(x_1(0)=0\) y\(x_2(0)=0\). El primer auto está viajando en\(3\:\frac{\text{m}}{\text{s}}\), entonces\(x'_1(0)=3\) y el segundo auto arranca en reposo, entonces\(x'_2(0)=0\). Las primeras condiciones dice

\[ \vec{0} = \vec{x}(0)= \left[ \begin{array}{c} a_1+ a_2 \\ a_1-2a_2 \end{array} \right]. \nonumber \]

No es difícil de ver eso\(a_1=a_2=0\). Nos fijamos\(a_1=0\) y\(a_2=0\) entramos\(\vec{x}(t)\) y diferenciamos para obtener

\[ \vec{x}'(t)= \left[ \begin{array}{c} b_1+ \sqrt3 b_2 \cos(\sqrt3 t)\\ b_1- 2 \sqrt3 b_2 \cos(\sqrt3 t) \end{array} \right]. \nonumber \]

Entonces

\[ \left[ \begin{array}{c} 3\\ 0 \end{array} \right] = \vec{x}'(0)= \left[ \begin{array}{c} b_1+ \sqrt3 b_2 \\ b_1- 2 \sqrt3 b_2 \end{array} \right]. \nonumber \]

Resolviendo estas dos ecuaciones encontramos\(b_1 = 2\) y\(b_2 = \frac{1}{\sqrt3}\). De ahí que la posición de nuestros autos sea (hasta el impacto con la pared)

\[ \vec{x}= \left[ \begin{array}{c} 2t +\frac{1}{\sqrt3} \sin(\sqrt3 t) \\ 2t -\frac{2}{\sqrt3} \sin(\sqrt3 t)\end{array} \right] . \nonumber \]

Observe cómo la presencia del valor propio cero resultó en un término que contenía\(t\). Esto quiere decir que los carros irán viajando en la dirección positiva a medida que crezca el tiempo, que es lo que esperamos.

Lo que realmente nos interesa es la segunda expresión, la de\(x_2\). Nosotros tenemos\(x_2(t)= 2t -\frac{2}{\sqrt3} \sin(\sqrt3 t)\). Ver Figura\(\PageIndex{6}\) para la gráfica de\(x_2\) versus tiempo.

Figura\(\PageIndex{6}\): Posición del segundo carro en el tiempo (ignorando la pared).

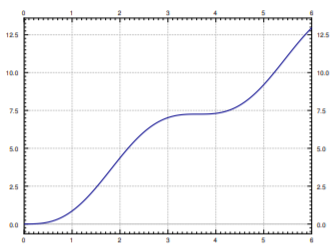
Apenas de la gráfica podemos ver que el tiempo de impacto será un poco más de 5 segundos del tiempo cero. Para ello tenemos que resolver la ecuación\(10=x_{2}(t)=2t-\frac{2}{\sqrt{3}}\sin (\sqrt{3}t)\). Usando una computadora (o incluso una calculadora gráfica) encontramos que\(t_{\text{impact}}\approx 5.22\) segundos.

En cuanto a la velocidad señalamos que\(x'_2 = 2-2 \cos(\sqrt3 t)\). Al momento del impacto (\(5.22\)segundos a partir de\(t=0\)) lo conseguimos\( x'_2(t_{\rm{impact}}) \approx 3.85\).

La velocidad máxima es la máxima de\(2-2 \cos(\sqrt3 t)\), que es\(4\). Estamos viajando a casi la velocidad máxima cuando chocamos contra la pared.

Supongamos que Bob es una persona diminuta sentada en el auto 2. Bob tiene un Martini en la mano y le gustaría no derramarlo. Supongamos que Bob no derramaría su Martini cuando el primer auto se vincula con el auto 2, pero si el auto 2 choca contra la pared a cualquier velocidad mayor que cero, Bob derramará su bebida. Supongamos que Bob puede mover el auto 2 a unos metros hacia o lejos de la pared (no puede llegar hasta la pared, ni puede salirse del camino del primer auto). ¿Hay una distancia “segura” para que esté? ¿Una distancia tal que el impacto con la pared sea a velocidad cero?

La respuesta es sí. Mirando Figura\(\PageIndex{6}\), notamos la “meseta” entre\(t=3\) y\(t=4\). Hay un punto donde la velocidad es cero. Para encontrarla tenemos que resolver\(x'_2(t)=0\). Esto es cuándo\(\cos(\sqrt3 t) = 1\) o en otras palabras cuándo\(t=\frac{2 \pi}{\sqrt3}, \frac{4 \pi}{\sqrt3}, \ldots\) y así sucesivamente. Enchufamos el primer valor a obtener\( x_2 \left( \frac{2 \pi}{\sqrt3} \right)=\frac{4 \pi}{\sqrt3} \approx 7.26 \). Por lo que una distancia “segura” es de unos 7 y un cuarto metros de la pared.

Alternativamente Bob podría alejarse de la pared hacia el auto entrante 2 donde está otra distancia segura\( \frac{8 \pi}{\sqrt3 } \approx 14.51\) y así sucesivamente, usando todos los diferentes\(t\) tales que\(x'_2(t)=0\). Desde luego siempre\(t=0\) es una solución aquí, correspondiente a\(x_2=0\), pero eso significa pararse justo en la pared.

Oscilaciones Forzadas

Finalmente pasamos a las oscilaciones forzadas. Supongamos que ahora nuestro sistema es

\[\label{eq:30} \vec{x}'' = A \vec{x} + \vec{F} \cos(\omega t). \]

Es decir, estamos agregando forzamiento periódico al sistema en la dirección del vector\(\vec{F}\).

Como antes, este sistema solo requiere que encontremos una solución en particular\(\vec{x}_p\), agregarla a la solución general del sistema homogéneo asociado\(\vec{x}_c\), y tendremos la solución general para\(\eqref{eq:30}\). Supongamos que no\(\omega\) es una de las frecuencias naturales de\( \vec{x}'' = A \vec{x}\), entonces podemos adivinar

\[ \vec{x}_p= \vec{c} \cos(\omega t), \nonumber \]

donde\(\vec{c}\) es un vector constante desconocido. Tenga en cuenta que no necesitamos usar seno ya que solo hay segundas derivadas. Resolvemos\(\vec{c}\) para encontrar\(\vec{x}_p\). Este es realmente solo el método de coeficientes indeterminados para los sistemas. Diferenciémonos\(\vec{x}_p\) dos veces para obtener

\[ \vec{x}''_p= -\omega^2 \vec{c} \cos(\omega t). \nonumber \]

Enchufe\(\vec{x}_p\) y\(\vec{x}''_p\) dentro de la ecuación\(\eqref{eq:30}\):

\[\overbrace{ -\omega^2 \vec{c} \cos (\omega t) }^{{\vec{x}_p}''} = \overbrace{ A \vec{c} \cos (\omega t) }^{A \vec{x}_p} + \vec{F} \cos (\omega t) . \nonumber \]

Cancelamos el coseno y reorganizamos la ecuación para obtener

\[ (A + \omega^2 I) \vec{c} = - \vec{F}. \nonumber \]

Entonces

\[ \vec{c} = (A + \omega^2 I)^{-1} (- \vec{F}). \nonumber \]

Por supuesto esto sólo es posible si\( (A + \omega^2 I)= (A -(- \omega^2) I)\) es invertible. Esa matriz es invertible si y sólo si no\(- \omega^2\) es un valor propio de\(A\). Eso es cierto si y sólo si no\(\omega\) es una frecuencia natural del sistema.

Simplificamos un poco las cosas. Si queremos tener el término forzoso para estar en las unidades de fuerza, digamos Newtons, entonces debemos escribir\[M \vec{x}'' = K \vec{x} + \vec{G} \cos(\omega t) . \nonumber \]

Si entonces escribimos las cosas en términos de\(A = M^{-1} K\), tenemos\[\vec{x}'' = M^{-1}K \vec{x} + M^{-1} \vec{G} \cos(\omega t) \qquad \text{or} \qquad \vec{x}'' = A \vec{x} + \vec{F} \cos(\omega t) , \nonumber \]

donde\(\vec{F} = M^{-1} \vec{G}\).

Ejemplo\(\PageIndex{3}\)

Tomemos el ejemplo en Figura\(\PageIndex{2}\) con los mismos parámetros que antes:\(m_1=2, m_2=1, k_1= 4,\) y\(k_2=2\). Ahora supongamos que hay una fuerza que\( 2 \cos(3t)\) actúa sobre el segundo carro.

La ecuación es

\[\begin{bmatrix} 2 & 0 \\ 0 & 1 \end{bmatrix} {\vec{x}}'' = \begin{bmatrix} -4 & 2 \\ 2 & -2 \end{bmatrix} \vec{x} + \begin{bmatrix} 0 \\ 2 \end{bmatrix} \cos (3 t) \qquad \text{or} \qquad {\vec{x}}'' = \begin{bmatrix} -3 & 1 \\ 2 & -2 \end{bmatrix} \vec{x} + \begin{bmatrix} 0 \\ 2 \end{bmatrix} \cos (3 t) . \nonumber \]

Se resolvió la ecuación homogénea asociada antes y se encontró que la solución complementaria era

\[ \vec{x}_c= \left[ \begin{array}{c} 1 \\ 2 \end{array} \right] (a_1 \cos(t) + b_1 \sin(t)) + \left[ \begin{array}{c} 1 \\ -1 \end{array} \right] (a_2 \cos(2t) + b_2 \sin(2t)). \nonumber \]

Las frecuencias naturales son\(1\) y\(2\). De ahí\(3\) que como no sea una frecuencia natural, podemos intentarlo\( \vec{c} \cos(3t)\). Nosotros invertimos\((A+3^2 I)\):

\[ \left( \left[ \begin{array}{cc} -3 & 1 \\ 2 & -2 \end{array} \right] + 3^2 I \right)^{-1}= \left[ \begin{array}{cc} 6 & 1 \\ 2 & 7 \end{array} \right]^{-1}= \left[ \begin{array}{cc} \frac{7}{40} & \frac{-1}{40} \\ \frac{-1}{20} & \frac{3}{20} \end{array} \right]. \nonumber \]

Por lo tanto,

\[ \vec{c}= (A+\omega^2 I)^{-1} (- \vec{F})= \left[ \begin{array}{cc} \frac{7}{40} & \frac{-1}{40} \\ \frac{-1}{20} & \frac{3}{20} \end{array} \right] \left[ \begin{array}{c} 0 \\ -2 \end{array} \right] = \left[ \begin{array}{c} \frac{1}{20} \\ \frac{-3}{10} \end{array} \right]. \nonumber \]

Combinando con lo que conocemos la solución general del problema homogéneo asociado a ser, obtenemos que la solución general a\(\vec{x}''= A \vec{x} +\vec{F} \cos(\omega t)\) es

\[ \vec{x} = \vec{x}_c + \vec{x}_p = \left[ \begin{array}{c} 1 \\ 2 \end{array} \right] (a_1 \cos(t) + b_1 \sin(t)) + \left[ \begin{array}{c} 1 \\ -1 \end{array} \right] (a_2 \cos(2t) + b_2 \sin(2t)) + \left[ \begin{array}{c} \frac{1}{20} \\ \frac{-3}{10} \end{array} \right] \cos(3t). \nonumber \]

Las constantes\(a_1, a_2, b_1,\) y luego\(b_2\) deben ser resueltas por dadas las condiciones iniciales.

Tenga en cuenta que dada la fuerza\(\vec{f}\), escribimos la ecuación como\(M\vec{x}''=K\vec{x}+\vec{f}\) para acertar las unidades. Entonces escribimos\(\vec{x}''=M^{-1}K\vec{x}+M^{-1}\vec{f}\). El término\(\vec{g}=M^{-1}\vec{f}\) en\(\vec{x}''=A\vec{x}+\vec{g}\) es en unidades de fuerza por unidad de masa.

Si\(\omega\) es una frecuencia natural del sistema se produce resonancia porque tendremos que probar una solución particular de la forma

\[ \vec{x}_p = \vec{c}t \sin(\omega t)+ \vec{d}t \cos(\omega t) . \nonumber \]

Eso es asumiendo que los valores propios de la matriz de coeficientes son distintos. A continuación, tenga en cuenta que la amplitud de esta solución crece sin ataduras a medida\(t\) que crece.