3.E: Sistemas de ODEs (Ejercicios)
- Page ID
- 115448
Estos son ejercicios de tarea para acompañar el mapa de texto "Ecuaciones Diferenciales para Ingeniería" de Libl. Se trata de un libro de texto dirigido a un primer curso de un semestre sobre ecuaciones diferenciales, dirigido a estudiantes de ingeniería. El requisito previo para el curso es la secuencia básica de cálculo.
3.1 Introducción a los Sistemas de ODEs
Encuentre la solución general de\( x'_1 = x_2 - x_1 + t, x'_2 = x_2\).
Encuentra la solución general de\( x'_1 = 3x_1 - x_2 + e^t, x'_2 = x_1 \).
Escribir\( ay'' + by' + cy = f(x) \) como un sistema de primer orden de ODEs.
Escribir\( x'' + y^2y' - x^3 = \sin (t), y'' + {(x' + y')}^2 - x = 0\) como un sistema de primer orden de ODEs.
Supongamos que dos masas en carros sobre superficie sin fricción están en desplazamientos\(x_{1}\) y\(x_{2}\) como en el Ejemplo 3.1.3. Supongamos que un cohete aplica fuerza\(F\) en la dirección positiva sobre el carro\(x_{1}\). Establecer el sistema de ecuaciones.
Supongamos que los tanques son como en el Ejemplo 3.1.2\(V\), comenzando ambos en volumen, pero ahora el caudal del tanque 1 al tanque 2 es\(r_{1}\), y el caudal del tanque 2 al tanque uno es\(r_{2}\). Observe que los volúmenes ahora no son constantes. Establecer el sistema de ecuaciones.
Encuentre la solución general para\( y'_1 = 3y_1, y'_2 = y_1 + y_2, y'_3 = y_1 + y_3 \).
- Contestar
-
\(y_{1}=C_{1}e^{3x}\),\(y_{2}=y(x)=C_{2}e^{x}+\frac{C_{1}}{2}e^{3x}\),\(y_{3}=y(x)=C_{3}e^{x}+\frac{C_{1}}{2}e^{3x}\)
Resolver\( y' = 2x, x' = x + y, x(0) = 1, y(0) = 3\).
- Contestar
-
\(x=\frac{5}{3}e^{2t}-\frac{2}{3}e^{-t}\),\(y=\frac{5}{3}e^{2t}+\frac{4}{3}e^{-t}\)
Escribir\( x''' = x + t \) como sistema de primer orden.
- Contestar
-
\(x_{1}'=x_{2}\),\(x_{2}'=x_{3}\),\(x_{3}'=x_{1}+t\)
Escribir\( y''_1 + y_1 + y_2 = t y''_2 + y_1 - y_2 = t^2 \) como sistema de primer orden.
- Contestar
-
\(y_{3}'+y_{1}+y_{2}=t\),\(y_{4}'+y_{1}-y_{2}=t^{2}\),\(y_{1}'=y_{3}\),\(y_{2}'=y_{4}\)
Supongamos que dos masas en carros sobre superficie sin fricción están en desplazamientos\(x_{1}\) y\(x_{2}\) como en el Ejemplo 3.1.3. Supongamos que el desplazamiento inicial es\(x_{1}(0)=x_{2}(0)=0\), y la velocidad inicial es\(x_{1}'(0)=x_{2}'(0)=a\) para algún número\(a\). Usa tu intuición para resolver el sistema, explica tu razonamiento.
- Contestar
-
\(x_{1}=x_{2}=at\). La explicación de la intuición se deja al lector.
Supongamos que los tanques son como en el Ejemplo 3.1.2 excepto que el agua limpia fluye a la velocidad\(s\) litros por segundo al tanque 1, y la salmuera fluye fuera del tanque 2 y hacia la alcantarilla también a razón de\(s\) litros por segundo.
- Dibuja el cuadro.
- Establecer el sistema de ecuaciones.
- Intuitivamente, lo que sucede como\(t\) va al infinito, explique.
- Contestar
-
- Izquierda al lector
- \(x_{1}'=\frac{r}{V}(x_{2}-x_{1})\),\(x_{2}'=\frac{r}{V}x_{1}-\frac{r-s}{V}x_{2}\).
- Como\(t\) va al infinito, ambos\(x_{1}\) y\(x_{2}\) van a cero, la explicación se deja al lector.
3.2: Matrices y sistemas lineales
Resuelve\( \begin {bmatrix} 1 & 2 \\ 3 & 4 \end {bmatrix} \vec {x} = \begin {bmatrix} 5 \\ 6 \end {bmatrix} \) mediante el uso de matriz inversa.
Calcular determinante de\( \begin {bmatrix} 9 & -2 & -6 \\ -8 & 3 & 6 \\ 10 & -2 & -6 \end {bmatrix}\).
Calcular determinante de\( \begin {bmatrix} 1 & 2 & 3 & 1 \\ 4 & 0 & 5 & 0 \\ 6 & 0 & 7 & 0 \\ 8 & 0 & 10 & 1 \end {bmatrix} \). Consejo: Expandir a lo largo de la fila o columna adecuada para simplificar los cálculos.
Calcular inverso de\( \begin {bmatrix} 1 & 2 & 3 \\ 1 & 1 & 1 \\ 0 & 1 & 0 \end {bmatrix} \).
¿Para qué\( \begin {bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & h \end {bmatrix} \) no\(h\) es invertible? ¿Sólo hay uno de esos\(h\)? ¿Hay varios? ¿Infinitamente muchos?
¿Para qué\( \begin {bmatrix} h & 1 & 1 \\ 0 & h & 0 \\ 1 & 1 & h \end {bmatrix} \) no\(h\) es invertible? Encuentra todos esos\(h\).
Resolver\( \begin {bmatrix} 9 & -2 & -6 \\ -8 & 3 & 6 \\ 10 & -2 & -6 \end {bmatrix} \vec {x} = \begin {bmatrix} 1 \\ 2 \\ 3 \end {bmatrix} \).
Resolver\( \begin {bmatrix} 5 & 3 & 7 \\ 8 & 4 & 4 \\ 6 & 3 & 3 \end {bmatrix} \vec{x} = \begin {bmatrix} 2 \\ 0 \\ 0 \end {bmatrix} \).
Resolver\( \begin {bmatrix} 3 & 2 & 3 & 0 \\ 3 & 3 & 3 & 3 \\ 0 & 2 & 4 & 2 \\ 2 & 3 & 4 & 3 \end {bmatrix} \vec {x} = \begin {bmatrix} 2 \\ 0 \\ 4 \\ 1 \end {bmatrix} \).
Encuentra 3\( 2 \times 2 \) matrices distintas de cero\( A, B, \) y\(C\) tal que\( AB = AC \) pero\( B \ne C \).
Determinante informático de\( \begin {bmatrix} 1 & 1 & 1 \\ 2 & 3 & -5 \\ 1 & -1 & 0 \end {bmatrix} \)
- Contestar
-
\(-15\)
Encuentra\( t \) tal que no\( \begin {bmatrix} 1 & t \\ -1 & 2 \end {bmatrix} \) sea invertible.
- Contestar
-
\(-2\)
Resolver\( \begin {bmatrix} 1 & 1 \\ 1 & -1 \end {bmatrix} \vec{x} = \begin {bmatrix} 10 \\ 20 \end {bmatrix} \).
- Contestar
-
\(\vec{x}=\left[\begin{array}{c}{15}\\{-5}\end{array}\right]\)
Supongamos que\( a, b, c \) son números distintos de cero. Let\( M = \begin {bmatrix} a & 0 \\ 0 & b \end {bmatrix}, N = \begin {bmatrix} a & 0 & 0 \\ 0 & b & 0 \\ 0 & 0 & c \end {bmatrix} \).
- \(M^{-1} \)Cómpiate.
- \( N^{-1} \)Cómpiate.
- Contestar
-
- \(\left[\begin{array}{cc}{\frac{1}{a}}&{0}\\{0}&{\frac{1}{b}}\end{array}\right]\)
- \(\left[\begin{array}{ccc}{\frac{1}{a}}&{0}&{0}\\{0}&{\frac{1}{b}}&{0}\\{0}&{0}&{\frac{1}{c}}\end{array}\right]\)
Escribe el sistema\( x'_1 = 2x_1-3tx_2+\sin t\) y\(x'_2=e^t\,x_1 - 3x_2 + \cos t\) en la forma\(\vec{x}'=P(t)\, \vec{x} + \vec{f}(t)\).
- Verificar que el sistema\( \vec{x}' = \begin{bmatrix} 1&3 \\ 3&1 \end{bmatrix} \vec{x} \) cuente con las dos soluciones\( \begin{bmatrix} 1\\1 \end{bmatrix}e^{4t} \) y\(\begin{bmatrix} 1\\-1\end{bmatrix} e^{-2t} \).
- Anote la solución general.
- Anote la solución general en la forma\(x_1 = ?\),\(x_2 = ? \) (es decir, anote una fórmula para cada elemento de la solución).
V erificar eso\( \begin{bmatrix} 1\\1 \end{bmatrix}e^t\) y\(\begin{bmatrix} 1\\-1 \end{bmatrix} e^t \) son linealmente independientes. Consejo: Solo tienes que enchufar\(t=0\).
Verificar que\(\begin{bmatrix} 1\\1\\0 \end{bmatrix}e^t\) y\(\begin{bmatrix}1\\-1\\1 \end{bmatrix}e^t \) y\(\begin{bmatrix} 1\\-1\\1 \end{bmatrix}e^{2t} \) son linealmente independientes. Pista: Debes ser un poco más complicado que en el ejercicio anterior.
\(\begin{bmatrix}t\\t^2 \end{bmatrix} \)Verifíquelo y\(\begin{bmatrix} t^3\\t^4 \end{bmatrix} \) sean linealmente independientes.
Toma el sistema\(x_{1}'+x_{2}'=x_{1}\),\(x_{1}'-x_{2}'=x_{2}\).
- Escríbelo en la forma\(A\vec{x}'=B\vec{x}\) para matrices\(A\) y\(B\).
- Compute\(A^{-1}\) y utilícelo para escribir el sistema en el formulario\(\vec{x}'=P\vec{x}\).
¿Son\( \begin{bmatrix} e^{2t}\\e^t \end{bmatrix} \) y\( \begin{bmatrix} e^t\\e^{2t} \end{bmatrix} \) linealmente independientes? Justificar.
- Contestar
-
Sí.
¿Son\( \begin{bmatrix} cosh(t) \\ 1 \end{bmatrix} \),\(\begin{bmatrix} e^t \\1 \end{bmatrix} \) y\( \begin{bmatrix} e^{-t} \\1 \end{bmatrix} \) linealmente independientes? Justificar.
- Contestar
-
No. \(2\left[\begin{array}{c}{\cosh (t)}{1}\end{array}\right]-\left[\begin{array}{c}{e^{t}}\\{1}\end{array}\right]-\left[\begin{array}{c}{e^{-t}}\\{1}\end{array}\right]=\vec{0}\)
Escribir\(x' = 3x -y+e^t\) and \(y'=tx\) en notación matricial.
- Contestar
-
\(\left[\begin{array}{c}{x}\\{y}\end{array}\right]'=\left[\begin{array}{cc}{3}&{-1}\\{t}&{0}\end{array}\right]\left[\begin{array}{c}{x}\\{y}\end{array}\right]+\left[\begin{array}{c}{e^{t}}\\{0}\end{array}\right]\)
- Escribir\(x'_1=2t\,x_2\) and \(x'_2=2t\,x_2\) en notación matricial.
- Resuelve y escribe la solución en notación matricial. Agrega texto de ejercicios aquí.
- Contestar
-
- \(\vec{x}'=\left[\begin{array}{cc}{0}&{2t}\\{0}&{2t}\end{array}\right]\vec{x}\)
- \(\vec{x}=\left[\begin{array}{c}{C_{2}e^{t^{2}}+C_{1}} \\ {C_{2}e^{t^{2}}}\end{array}\right]\)
Dejar\(A\) ser una\(3 \times 3\) matriz con un valor propio de\(3\) y un vector propio correspondiente\(\vec{v}= \left[ \begin{array}{c} 1 \\ -1 \\ 3 \end{array} \right]\). Encontrar\(A \vec{v}\).
- Encuentre la solución general de\( x'_1=2x_1, x'_2=3x_2\) usar el método de valor propio (primero escriba el sistema en el formulario\(\vec{x}'=A\vec{x}\)).
- Resuelve el sistema resolviendo cada ecuación por separado y verifica que obtienes la misma solución general.
Encuentre la solución general de\(x'_1 = 3x_1 +x_2, x'_2 =2x_1+4x_2\) usar el método de valor propio.
Encuentre la solución general de\(x'_1 =x_1-2x_2, x'_2=2x_1 x_2\) usar el método de valor propio. No utilice exponenciales complejos en su solución.
- C ompute los valores propios y los vectores propios de\(A= \left[ \begin{array}{ccc} 9 & -2 & -6 \\ -8 & 3 & 6 \\ 10 & -2 & -6 \end{array} \right] \).
- Encuentra la solución general de\(\vec{x}'=A\vec{x}\).
Calcular valores propios y vectores propios de\( \left[ \begin{array}{ccc} -2 & -1 & -1 \\ 3 & 2 & 1 \\ -3 & -1 & 0 \end{array} \right].\)
\(a, b, c, d, e, f\)Dejen ser números. Encuentra los valores propios de\( \left[ \begin{array}{ccc} a & b & c \\ 0 & d & e \\ 0 & 0 & f \end{array} \right].\)
- Calcular valores propios y vectores propios de\(A= \left[ \begin{array}{ccc} 1 & 0 & 3 \\ -1 & 0 & 1 \\ 2 & 0 & 2 \end{array} \right] \).
- Resuelve el sistema\(\vec{x}'=A\vec{x}\).
- Contestar
-
- Valores propios:\(4,\:0,\:-1\) vectores propios:\(\left[\begin{array}{c}{1}\\{0}\\{1}\end{array}\right]\),\(\left[\begin{array}{c}{0}\\{1}\\{0}\end{array}\right]\),\(\left[\begin{array}{c}{3}\\{5}\\{-2}\end{array}\right]\)
- \(\vec{x}=C_{1}\left[\begin{array}{c}{1}\\{0}\\{1}\end{array}\right] e^{4t}+C_{2}\left[\begin{array}{c}{0}\\{1}\\{0}\end{array}\right]+C_{3}\left[\begin{array}{c}{3}\\{5}\\{-2}\end{array}\right]\)
- Calcular valores propios y vectores propios de\(A= \left[ \begin{array}{cc} 1 & 1 \\ -1 & 0 \end{array} \right].\)
- Resuelve el sistema\(\vec{x}'=A\vec{x}\).
- Contestar
-
- Valores propios:\(\frac{1+\sqrt{3}i}{2}\),\(\frac{1-\sqrt{3}i}{2}\), vectores propios:\(\left[\begin{array}{c}{-2}\\{1-\sqrt{3}i}\end{array}\right]\),\(\left[\begin{array}{c}{-2}\\{1+\sqrt{3}i}\end{array}\right]\)
- \(\vec{x}=C_{1}e^{t/2}\left[\begin{array}{c}{-2\cos\left(\frac{\sqrt{3}t}{2}\right)}\\{\cos\left(\frac{\sqrt{3}t}{2}\right)+\sqrt{3}\sin\left(\frac{\sqrt{3}t}{2}\right)}\end{array}\right]+C_{2}e^{t/2}\left[\begin{array}{c}{-2\sin\left(\frac{\sqrt{3}t}{2}\right)}\\{\sin\left(\frac{\sqrt{3}t}{2}\right)-\sqrt{3}\cos\left(\frac{\sqrt{3}t}{2}\right)}\end{array}\right]\)
Resuelve\( x'_1=x_2, x'_2=x_1\) usando el método del valor propio.
- Contestar
-
\(\vec{x}=C_{1}\left[\begin{array}{c}{1}\\{1}\end{array}\right]e^{t}+C_{2}\left[\begin{array}{c}{1}\\{-1}\end{array}\right]e^{-t}\)
Resuelve\( x'_1=x_2, x'_2=-x_1\) usando el método del valor propio.
- Contestar
-
\(\vec{x}=C_{1}\left[\begin{array}{c}{\cos(t)}\\{-\sin(t)}\end{array}\right]+C_{2}\left[\begin{array}{c}{\sin(t)}\\{\cos(t)}\end{array}\right]\)
3.5: Sistemas bidimensionales y sus campos vectoriales
Toma la ecuación\(m{x}'' + c{x}'+kx =0 \), con\( m>0, c\geq 0, k>0 \) para el sistema masa-resorte.
- Convertir esto en un sistema de ecuaciones de primer orden.
- Clasifica por\(k\) qué\(m\)\(c\),, obtienes qué comportamiento.
- ¿Puedes explicar desde la intuición física por qué no obtienes aquí todos los diferentes tipos de comportamiento?
¿Puedes encontrar lo que sucede en el caso cuando\( P =\begin{bmatrix} 1&1\\ 0&1 \end{bmatrix} \)? En este caso se repite el valor propio y solo hay un vector propio. ¿A qué imagen se ve esta?
¿Puedes encontrar lo que sucede en el caso cuando\( P = \begin{bmatrix} 1&1\\1&1 \end{bmatrix} \)? ¿Esto se parece a alguna de las imágenes que hemos dibujado?
¿Qué comportamientos son posibles si\(P\) es diagonal, es decir\(P=\left[\begin{array}{cc}{a}&{0}\\{0}&{b}\end{array}\right]\)? Se puede asumir eso\(a\) y no\(b\) son cero.
Tome el sistema del Ejemplo 3.1.2,\(x_{1}'=\frac{r}{V}(x_{2}-x_{1})\),\(x_{2}'=\frac{r}{V}(x_{1}-x_{2})\). Como decíamos, uno de los valores propios es cero. Cuál es el otro valor propio, cómo se ve la imagen y qué sucede cuando\(t\) va al infinito.
Describir el comportamiento de los siguientes sistemas sin resolver:
- \(x' = x + y,\quad y' = x- y\)
- \(x_1' = x_1 + x_2,\quad x_2' = 2x_2 \)
- \(x_1' = -2x_2,\quad x_2' = 2x_1 \)
- \(x' = x+ 3y,\quad y' = -2x-4y \)
- \(x' = x - 4y,\quad y' = -4x+y \)
- Contestar
-
- Dos valores propios:\(\pm\sqrt{2}\) por lo que el comportamiento es una silla de montar.
- Dos valores propios:\(1\) y\(2\), por lo que el comportamiento es una fuente.
- Dos valores propios:\(\pm 2i\), por lo que el comportamiento es un centro (elipses).
- Dos valores propios:\(−1\) y\(−2\), por lo que el comportamiento es un sumidero.
- Dos valores propios:\(5\) y\(−3\), así el comportamiento es una silla de montar.
Supongamos que\(\vec{x} = A \vec{x} \) donde\(A\) es un\(2 \times 2\) matrix with eigenvalues\( 2\pm i\). Describe el comportamiento.
- Contestar
-
Fuente espiral.
Tomar\( \begin{bmatrix} x\\y \end{bmatrix}' = \begin{bmatrix} 0&1 \\0&0 \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix} \). Dibuja el campo vectorial y describe el comportamiento. ¿Es uno de los comportamientos que hemos visto antes?
- Contestar
-
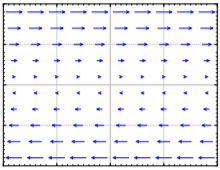
La solución no se mueve a ningún lado si\(y=0\). Cuando\(y\) es positivo, la solución se mueve (con velocidad constante) en la\(x\) dirección positiva. Cuando\(y\) es negativo, la solución se mueve (con velocidad constante) en la\(x\) dirección negativa. No es uno de los comportamientos que vimos. Tenga en cuenta que la matriz tiene un valor propio doble\(0\) y la solución general es\(x=C_{1}t+C_{2}\) y\(y=C_{1}\), que concuerda con la descripción
3.6: Sistemas y aplicaciones de segundo orden
Encuentre una solución particular para
\[ \vec{x}'' = \left[ \begin{array}{cc} -3 & 1 \\ 2 & -2 \end{array} \right] \vec{x} + \left[ \begin{array}{c} 0 \\ 2 \end{array} \right] \cos(2t). \]
Tomemos el ejemplo de la Figura 3.6.3 con los mismos parámetros que antes:\(m_1=2, k_1=4,\) y a\(k_2=2,\) excepción de\(m_2\), que se desconoce. Supongamos que hay una fuerza\( \cos(5t)\) que actúa sobre la primera masa. Encuentra un\(m_2\) tal que exista una solución particular donde la primera masa no se mueva.
T su idea se llama amortiguación dinámica. En la práctica habrá una pequeña cantidad de amortiguación y así cualquier solución transitoria desaparecerá y después del tiempo suficiente, la primera masa siempre se detendrá.
Tomemos el Ejemplo 3.6.2, pero que en el momento del impacto, el carro 2 se mueve hacia la izquierda a la velocidad de\(3\:\frac{\text{m}}{\text{s}}\).
- Encuentra el comportamiento del sistema después de la conexión.
- ¿El segundo auto chocará contra la pared o se irá alejando de la pared a medida que pasa el tiempo?
- ¿A qué velocidad tendría que viajar el primer automóvil para que el sistema esencialmente se mantenga en su lugar después de la conexión?
Tomemos el ejemplo de la Figura 3.6.2 con parámetros\(m_1=m_2=1, k_1=k_2=1\). ¿Existe un conjunto de condiciones iniciales para las que se mueve el primer carro pero el segundo no? Si es así, encuentra esas condiciones. Si no, argumenta por qué no.
Encuentre la solución general para
\[ \left[ \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 3 \end{array} \right] \vec{x}''=\left[ \begin{array}{ccc} -3 & 0 & 0 \\ 2 & -4 & 0 \\ 0 & 6 & -3 \end{array} \right] \vec{x}+\left[ \begin{array}{c} \cos(2t) \\ 0 \\ 0 \end{array} \right].\]
- Contestar
-
\(\vec{x}=\left[\begin{array}{c}{1}\\{-1}\\{1}\end{array}\right]\left( a_{1}\cos (\sqrt{3} t)+b_{1}\sin (\sqrt{3} t)\right) +\left[\begin{array}{c}{0}\\{1}\\{-2}\end{array}\right]\left( a_{2}\cos (\sqrt{2} t)+b_{2}\sin (\sqrt{2} t)\right) +\left[\begin{array}{c}{0}\\{0}\\{1}\end{array}\right]\left( a_{3}\cos (t)+b_{3}\sin (t)\right) +\left[\begin{array}{c}{-1}\\{1/2}\\{2/3}\end{array}\right]\cos (2t)\)
Supongamos que hay tres carros de igual masa\(m\) y conectados por dos resortes de constante\(k\) (y sin conexiones a muros). Configura el sistema y encuentra su solución general.
- Contestar
-
\(\left[\begin{array}{ccc}{m}&{0}&{0}\\{0}&{m}&{0}\\{0}&{0}&{m}\end{array}\right]\vec{x}''=\left[\begin{array}{c}{-k}&{k}&{0}\\{k}&{-2k}&{k}\\{0}&{k}&{-k}\end{array}\right]\vec{x}\).
Solución:\(\vec{x}=\left[\begin{array}{c}{1}\\{-2}\\{1}\end{array}\right]\left( a_{1}\cos (\sqrt{3k/m} t)+b_{1}\sin (\sqrt{3k/m} t)\right) + \left[\begin{array}{c}{1}\\{0}\\{-1}\end{array}\right]\left( a_{2}\cos (\sqrt{k/m} t)+b_{2}\sin (\sqrt{k/m} t)\right) +\left[\begin{array}{c}{1}\\{1}\\{1}\end{array}\right](a_{3}t+b_{3})\).
Supongamos un carro de masa\(2\text{ kg}\) is attached by a spring of constant \(k=1\) a un carro de masa\(3\text{ kg}\), which is attached to the wall by a spring also of constant \(k=1\). Supongamos que la posición inicial del primer carro es la\(1\) meter in the positive direction from the rest position, and the segunda masa comienza en la posición de reposo. Las masas no se mueven y son soltadas. Encuentra la posición de la segunda masa en función del tiempo.
- Contestar
-
\(x_{2}=\left(\frac{2}{5}\right)\cos\left(\sqrt{\frac{1}{6}}t\right)-\left(\frac{2}{5}\right)\cos (t)\)
3.7: Valores propios múltiples
Vamos\( A = \begin{bmatrix} 5&-3 \\3&-1 \end{bmatrix} \). Encuentra la solución general de\(\vec{x}' = A\vec{x}\).
Let\(A =\begin{bmatrix} 5&-4&4\\ 0&3&0 \\-2&4&-1\end{bmatrix}. \)
- ¿Cuáles son los valores propios?
- ¿Cuál es/son los defectos del (de los) valor (s) propio (s)?
- Encuentra la solución general de\(\vec{x}' = A\vec{x} \).
Vamos\( A = \begin{bmatrix} 2&1&0\\0&2&0\\0&0&2\end{bmatrix} \).
- ¿Cuáles son los valores propios?
- ¿Cuál es/son los defectos del (de los) valor (s) propio (s)?
- Encuentra la solución general de\(\vec{x}' = A\vec{x} \) de dos maneras diferentes y verifica que obtienes la misma respuesta.
Vamos\(A = \begin{bmatrix}0&1&2 \\ -1&-2&-2\\-4&4&7 \end{bmatrix} \).
- ¿Cuáles son los valores propios?
- ¿Cuál es/son los defectos del (de los) valor (s) propio (s)?
- Encuentra la solución general de\(\vec{x}' = A\vec{x} \).
Vamos\(A = \begin{bmatrix} 0&4&-2\\-1&-4&1\\0&0&-2 \end{bmatrix} \).
- ¿Cuáles son los valores propios?
- ¿Cuál es/son los defectos del (de los) valor (s) propio (s)?
- Encuentra la solución general de\(\vec{x}' = A \vec{x} \).
Vamos\(\begin{bmatrix} 2&1&-1\\ -1&0&2\\-1&-2&4 \end{bmatrix} \).
- ¿Cuáles son los valores propios?
- ¿Cuál es/son los defectos del (de los) valor (s) propio (s)?
- Encuentra la solución general de\(\vec{x}' = A \vec{x}\).
Supongamos que A es una\(2 \times 2 \) matriz con un valor propio repetido\(\lambda\). Supongamos que hay dos vectores propios linealmente independientes. \(A = \lambda I\)Demuéstralo.
Vamos\(A = \begin{bmatrix} 1&1&1\\1&1&1\\1&1&1 \end{bmatrix} \).
- ¿Cuáles son los valores propios?
- ¿Cuál es/son los defectos del (de los) valor (s) propio (s)?
- Encuentra la solución general de\(\vec{x}' = A \vec{x} \).
- Contestar
-
- \(3,\:0,\:0\)
- Sin defectos.
- \(\vec{x}=C_{1}\left[\begin{array}{c}{1}\\{1}\\{1}\end{array}\right]e^{3t}+C_{2}\left[\begin{array}{c}{1}\\{0}\\{-1}\end{array}\right]+C_{3}\left[\begin{array}{c}{0}\\{1}\\{-1}\end{array}\right]\)
Vamos\(A = \begin{bmatrix} 1&3&3 \\ 1&1&0 \\-1&1&2\end{bmatrix} \).
- ¿Cuáles son los valores propios?
- ¿Cuál es/son los defectos del (de los) valor (s) propio (s)?
- Encuentra la solución general de\(\vec{x}' = A \vec{x} \).
- Contestar
-
- \(1,\:1,\:2\)
- El valor propio\(1\) tiene un defecto de\(1\)
- \(\vec{x}=C_{1}\left[\begin{array}{c}{0}\\{1}\\{-1}\end{array}\right]e^{t}+C_{2}\left(\left[\begin{array}{c}{1}\\{0}\\{0}\end{array}\right]+t\left[\begin{array}{c}{0}\\{1}\\{-1}\end{array}\right]\right)e^{t}+C_{3}\left[\begin{array}{c}{3}\\{3}\\{-2}\end{array}\right]e^{2t}\)
Vamos\(A = \begin{bmatrix} 2&0&0 \\-1&-1&9\\0&-1&5\end{bmatrix} \).
- ¿Cuáles son los valores propios?
- ¿Cuál es/son los defectos del (de los) valor (s) propio (s)?
- Encuentra la solución general de\( \vec{x}'= A \vec{x}\).
- Contestar
-
- \(2,\:2,\:2\)
- El valor propio\(2\) tiene un defecto de\(2\)
- \(\vec{x}=C_{1}\left[\begin{array}{c}{0}\\{3}\\{1}\end{array}\right]e^{2t}+C_{2}\left(\left[\begin{array}{c}{0}\\{-1}\\{0}\end{array}\right]+t\left[\begin{array}{c}{0}\\{3}\\{1}\end{array}\right]\right)e^{2t}+C_{3}\left(\left[\begin{array}{c}{1}\\{0}\\{0}\end{array}\right]+t\left[\begin{array}{c}{0}\\{-1}\\{0}\end{array}\right]+\frac{t^{2}}{2}\left[\begin{array}{c}{0}\\{3}\\{1}\end{array}\right]\right)e^{2t}\)
Vamos\(A = \begin{bmatrix} a&a\\b&c\end{bmatrix} \), dónde\(a\),\(b\), y\(c\) son incógnitas. Supongamos que 5 es un valor propio duplicado del defecto 1, y supongamos que\(\begin{bmatrix} 1\\0 \end{bmatrix} \) es el autovector. Encuentra\(A \) y demuestra que solo hay una solución.
- Contestar
-
\(A=\left[\begin{array}{cc}{5}&{5}\\{0}&{5}\end{array}\right]\)
3.8: Exponenciales de Matriz
Usando la matriz exponencial, encontrar una solución matriz fundamental para el sistema,\(x' = 3x +y, y' = x+ 3y \).
Encuentra\(e^{tA} \) para la matriz\(A = \begin{bmatrix} 2&3\\0&2 \end{bmatrix} \).
Encuentre una solución de matriz fundamental para el sistema,\(x'_1 =7x_1 +4x_2 +12x_3,~~~ x'_2= x_1 + 2x_2 +x_3,~~~x'_3 = -3x_1 - 2x_2 -5x_3 \). Entonces encuentra la solución que satisfaga\( \vec{x} = \begin{bmatrix}0\\1\\-2\end{bmatrix} \).
Calcular la matriz exponencial\(e^A\) para\(A = \begin{bmatrix} 1&2\\0&2\end{bmatrix} \).
Supongamos\(AB=BA\). Demostrar que bajo este supuesto,\(e^{A+B} = e^A e^B \).
Usa Ejercicio\(\PageIndex{3.8.5}\) para demostrarlo\((e^A)^{-1} = e^{-A} \). En particular esto significa que\(e^A \) es invertible aunque A no lo sea.
Supongamos que\(A\) es una matriz con valores propios\(-1\)\(1\),, y vectores propios correspondientes\(\begin{bmatrix} 1\\1\end{bmatrix} \),\(\begin{bmatrix}0\\1\end{bmatrix} \).
- Encuentra matriz\(A\) con estas propiedades.
- Encuentre la solución de matriz fundamental para\(\vec{x}' = A \vec{x} \).
- Resolver el sistema en con condiciones iniciales\(\vec{x}(0) = \begin{bmatrix} 2\\3 \end{bmatrix} \).
Supongamos que\(A\) es una\(n \times n \) matriz con un valor propio repetido\(\lambda\) de multiplicidad n. Supongamos que hay n vectores propios linealmente independientes. Demostrar que la matriz es diagonal, en particular\(A = \lambda \mathit{I} \). Pista: Usa la diagonalización y el hecho de que la matriz de identidad se desplaza con cualquier otra matriz.
Vamos\(A =\begin{bmatrix} -1&-1\\1&-3 \end{bmatrix} \).
- Encontrar\(e^{tA} \).
- Resolver\(\vec{x}' = A \vec{x} \),\(\vec{x}(0) = \begin{bmatrix} 1\\-2 \end{bmatrix} \).
Vamos\(A = \begin{bmatrix} 1&2\\3&4 \end{bmatrix} \). \(e^{tA} \)Aproximado expandiendo la serie de potencia hasta el tercer orden.
Para cualquier entero positivo\(n\), busque una fórmula (o una receta)\(A^{n}\) para las siguientes matrices:
- \(\left[\begin{array}{cc}{3}&{0}\\{0}&{9}\end{array}\right]\)
- \(\left[\begin{array}{cc}{5}&{2}\\{4}&{7}\end{array}\right]\)
- \(\left[\begin{array}{cc}{0}&{1}\\{0}&{0}\end{array}\right]\)
- \(\left[\begin{array}{cc}{2}&{1}\\{0}&{2}\end{array}\right]\)
Calcular\(e^{tA} \) dónde\(A = \begin{bmatrix} 1&-2\\-2&1\end{bmatrix} \).
- Contestar
-
\(e^{tA}=\left[\begin{array}{cc}{\frac{e^{3t}+e^{-t}}{2}}&{\frac{e^{-t}-e^{3t}}{2}}\\{\frac{e^{-t}-e^{3t}}{2}}&{\frac{e^{3t}+e^{-t}}{2}}\end{array}\right]\)
Calcular\(e^{tA}\) dónde\(A=\begin{bmatrix} 1&-3&2\\-2&1&2\\-1&-3&4 \end{bmatrix} \).
- Contestar
-
\(e^{tA}=\left[\begin{array}{ccc}{2e^{3t}-4e^{2t}+3e^{t}}&{\frac{3e^{t}}{2}-\frac{3e^{3t}}{2}}&{-e^{3t}+4e^{2t}-3e^{t}}\\{2e^{t}-2e^{2t}}&{e^{t}}&{2e^{2t}-2e^{t}}\\{2e^{3t}-5e^{2t}+3e^{t}}&{\frac{3e^{t}}{2}-\frac{3e^{3t}}{2}}&{-e^{3t}+5e^{2t}-3e^{t}}\end{array}\right]\)
- Calcular\(e^{tA} \) dónde\(A = \begin{bmatrix} 3& -1\\1&1\end{bmatrix} \).
- Resolver\(\vec{x} ' = A \vec{x} \) para\( \vec{x}(0) = \begin{bmatrix} 1\\2 \end{bmatrix} \).
- Contestar
-
- \(e^{tA}=\left[\begin{array}{cc}{(t+1)e^{2t}}&{-te^{2t}}\\{te^{2t}}&{(1-t)e^{2t}}\end{array}\right]\)
- \(\vec{x}=\left[\begin{array}{c}{(1-t)e^{2t}}\\{(2-t)e^{2t}}\end{array}\right]\)
Calcular los primeros 3 términos (hasta el segundo grado) de la expansión Taylor de\(e^{tA} \) where\(A =\begin{bmatrix} 2&3\\2&2 \end{bmatrix} \) (Escribir como una sola matriz). Después utilízala para aproximar\(e^{0.1A} \).
- Contestar
-
\(\left[\begin{array}{cc}{1+2t+5t^{2}}&{3t+6t^{2}}\\{2t+4t^{2}}&{1+2t+5t^{2}}\end{array}\right]\)\(e^{0.1A}\approx\left[\begin{array}{cc}{1.25}&{0.36}\\{0.24}&{1.25}\end{array}\right]\)
Para cualquier entero positivo\(n\), busque una fórmula (o una receta)\(A^{n}\) para las siguientes matrices:
- \(\left[\begin{array}{cc}{7}&{4}\\{-5}&{-2}\end{array}\right]\)
- \(\left[\begin{array}{cc}{-3}&{4}\\{-6}&{-7}\end{array}\right]\)
- \(\left[\begin{array}{cc}{0}&{1}\\{1}&{0}\end{array}\right]\)
- Contestar
-
- \(\left[\begin{array}{cc}{5(3^{n})-2^{n+2}}&{4(3^{n})-2^{n+2}}\\{5(2^{n})-5(3^{n})}&{5(2^{n})-4(3^{n})}\end{array}\right]\)
- \(\left[\begin{array}{cc}{3-2(3^{n})}&{2(3^{n})-2}\\{3-3^{n+1}}&{3^{n+1}-2}\end{array}\right]\)
- \(\left[\begin{array}{cc}{1}&{0}\\{0}&{1}\end{array}\right]\)si\(n\) es par, y\(\left[\begin{array}{cc}{0}&{1}\\{1}&{0}\end{array}\right]\) si\(n\) es impar.
3.9: Sistemas no homogéneos
Encuentre una solución particular para\( x'=x+2y+2t,\: y'=3x+2y-4\),
- utilizando el método de factor de integración,
- usando descomposición de vectores propios,
- utilizando coeficientes indeterminados.
Encuentre la solución general para\( x'=4x+y-1,\: y'=x+4y-e^t\),
- utilizando el método de factor de integración,
- usando descomposición de vectores propios,
- utilizando coeficientes indeterminados.
Encuentre la solución general para\( x_1''=-6x_1+3x_2+ \cos(t),\: x''_2=2x_1-7x_2+ 3 \cos(t)\),
- usando descomposición de vectores propios,
- utilizando coeficientes indeterminados.
Encuentre la solución general para\( x''_1=-6x_1+3x_2 + \cos(2t),\: x''_2=2x_1-7x_2+ \cos(2t) \),
- usando descomposición de vectores propios,
- utilizando coeficientes indeterminados.
Toma la ecuación
\[ \vec{x}' = \left[ \begin{array}{cc} \frac{1}{t} & -1\\ 1 & \frac{1}{t} \end{array} \right] \vec{x}+ \left[ \begin{array}{c} t^2 \\ -t \end{array} \right]. \]
- Comprobar que\[ \vec{x}_c = c_1\left[ \begin{array}{c} t \sin t\\ -t \cos t \end{array} \right] + c_2\left[ \begin{array}{c} t \cos t\\ t \sin t \end{array} \right]\] es la solución complementaria.
- Utilice la variación de parámetros para encontrar una solución particular.
Encuentre una solución particular para\( x' = 5x +4y+t,\: y'=x+8y-t\),
- utilizando el método de factor de integración,
- usando descomposición de vectores propios,
- utilizando coeficientes indeterminados.
- Contestar
-
La solución general es (las soluciones particulares deben estar de acuerdo con una de estas):\(x(t)=C_{1}e^{9t}+4C_{2}e^{4t}-\frac{t}{3}-\frac{5}{54}\)\(y(t)=C_{1}e^{9t}-C_{2}e^{4t}+\frac{t}{6}+\frac{7}{216}\)
Encuentre una solución particular para\( x'=y+e^t,\: y'=x+e^t\),
- utilizando el método de factor de integración,
- usando descomposición de vectores propios,
- utilizando coeficientes indeterminados.
- Contestar
-
La solución general es (las soluciones particulares deben estar de acuerdo con una de estas):\(x(t)=C_{1}e^{t}+C_{2}e^{-t}+te^{t}\)\(y(t)=C_{1}e^{t}-C_{2}e^{-t}+te^{t}\)
Resolver\( x'_1=x_2+t, x'_2=x_1+t\) con condiciones iniciales\( x_1(0)=1, x_2(0)=2\), utilizando descomposición de vectores propios.
- Contestar
-
\(\vec{x}=\left[\begin{array}{c}{1}\\{1}\end{array}\right]\left(\frac{5}{2}e^{t}-t-1\right)+\left[\begin{array}{c}{1}\\{-1}\end{array}\right]\frac{-1}{2}e^{-t}\)
S olve\( x''_1=-3x_1+x_2+t, x''_2=9x_1+5x_2 +\cos(t)\) con condiciones iniciales\( x_1(0)=0, x_2(0)=0, x'_1(0)=0, x'_2(0)=0\), usando descomposición de vectores propios.
- Contestar
-
\(\vec{x}=\left[\begin{array}{c}{1}\\{9}\end{array}\right]\left(\left(\frac{1}{140}+\frac{1}{120\sqrt{6}}\right)e^{\sqrt{6}t}+\left(\frac{1}{140}+\frac{1}{120\sqrt{6}}\right)e^{-\sqrt{6}t}-\frac{t}{60}-\frac{\cos (t)}{70}\right) +\left[\begin{array}{c}{1}\\{-1}\end{array}\right]\left(\frac{-9}{80}\sin (2t)+\frac{1}{30}\cos (2t)+\frac{9t}{40}-\frac{\cos (t)}{30}\right)\)


