8.1: Linealización, Puntos Críticos y Equilibrios
- Page ID
- 115462
Excepto por algunos breves desvíos en el Capítulo 1, consideramos ecuaciones principalmente lineales. Las ecuaciones lineales son suficientes en muchas aplicaciones, pero en realidad la mayoría de los fenómenos requieren ecuaciones no lineales. Las ecuaciones no lineales, sin embargo, son notoriamente más difíciles de entender que las lineales, y muchos fenómenos nuevos y extraños aparecen cuando permitimos que nuestras ecuaciones sean no lineales.
No se preocupe, no perdimos todo este tiempo estudiando ecuaciones lineales. Las ecuaciones no lineales a menudo pueden aproximarse por unas lineales si solo necesitamos una solución “localmente”, por ejemplo, solo por un corto período de tiempo, o solo para ciertos parámetros. Comprender las ecuaciones lineales también puede darnos una comprensión cualitativa sobre un problema no lineal más general. La idea es similar a lo que hiciste en cálculo al tratar de aproximar una función por una línea con la pendiente correcta.
En la Sección 2.4 observamos el péndulo de masa\(m\) and length \(L\). The goal was to solve for the angle \(\theta(t)\) as a function of the time \(t\). The equation for the setup is the nonlinear equation
\[\theta'' + \frac{g}{L} \sin \theta = 0 . \nonumber \]
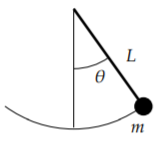
En lugar de resolver esta ecuación, resolvimos la ecuación lineal bastante más fácil
\[\theta'' + \frac{g}{L} \theta = 0 . \nonumber \]
Si bien la solución a la ecuación lineal no es exactamente lo que estábamos buscando, es más bien cercana a la original, siempre y cuando el ángulo\(\theta\) is small and the time period involved is short.
Podrías preguntar: ¿Por qué no resolvemos simplemente el problema no lineal? Bueno, puede ser muy difícil, poco práctico, o imposible de resolver analíticamente, dependiendo de la ecuación en cuestión. Puede que ni siquiera nos interese la solución real, puede que solo nos interese alguna idea cualitativa de lo que está haciendo la solución. Por ejemplo, ¿qué pasa a medida que el tiempo va al infinito?
Sistemas Autónomos y Análisis de Plano de Fase
Limitamos nuestra atención a un sistema autónomo bidimensional
\[x' = f(x,y) , \qquad y' = g(x,y) , \nonumber \]
donde\(f(x,y)\) and \(g(x,y)\) are functions of two variables, and the derivatives are taken with respect to time \(t\). Solutions are functions \(x(t)\) and \(y(t)\) such that
\[x'(t) = f\bigl(x(t),y(t)\bigr), \qquad y'(t) = g\bigl(x(t),y(t)\bigr) . \nonumber \]
La forma en que analizaremos el sistema es muy similar a la Sección 1.6, donde estudiamos una sola ecuación autónoma. Las ideas en dos dimensiones son las mismas, pero el comportamiento puede ser mucho más complicado.
Puede ser mejor pensar en el sistema de ecuaciones como la ecuación de un solo vector
\[\label{eq:1}\begin{bmatrix} x \\ y \end{bmatrix} ' = \begin{bmatrix} f(x,y) \\ g(x,y) \end{bmatrix} . \]
Al igual que en la Sección 3.1 dibujamos el retrato de fase (o diagrama de fases), donde cada punto\((x,y)\) corresponds to a specific state of the system. We draw the vector field given at each point \((x,y)\) by the vector \(\left[ \begin{smallmatrix} f(x,y) \\ g(x,y) \end{smallmatrix} \right]\). And as before if we find solutions, we draw the trajectories by plotting all points \(\bigl(x(t),y(t)\bigr)\) for a certain range of \(t\).
Considere la ecuación de segundo orden\(x''=-x+x^2\). Write this equation as a first order nonlinear system
\[x' = y , \qquad y' = -x+x^2 . \nonumber \]
El retrato de fase con algunas trayectorias se dibuja en la Figura\(\PageIndex{2}\).
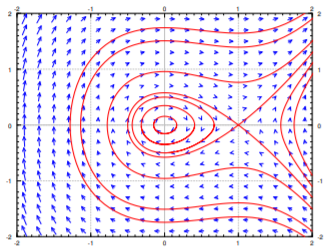
Del retrato de fase debe quedar claro que incluso este sencillo sistema tiene un comportamiento bastante complicado. Algunas trayectorias siguen oscilando alrededor del origen, y algunas van hacia el infinito. Volveremos a este ejemplo a menudo, y lo analizaremos completamente en esta (y la siguiente) sección.
Si nos acercamos al diagrama cerca de un punto donde no\(\left[ \begin{smallmatrix} f(x,y) \\ g(x,y) \end{smallmatrix} \right]\) es cero, entonces cerca las flechas apuntan generalmente esencialmente en esa misma dirección y tienen esencialmente la misma magnitud. En otras palabras, el comportamiento no es tan interesante cerca de tal punto. Por supuesto estamos asumiendo eso\(f(x,y)\) y\(g(x,y)\) somos continuos.
Concentrémonos en esos puntos del diagrama de fases anterior donde las trayectorias parecen comenzar, terminar o dar vueltas. Vemos dos puntos de este tipo:\((0,0)\) and \((1,0)\). The trajectories seem to go around the point \((0,0)\), and they seem to either go in or out of the point \((1,0)\). Estos puntos son precisamente aquellos puntos donde los derivados de ambos\(x\) and \(y\) are zero. Let us define the critical points as the points \((x,y)\) such that
\[ \begin{bmatrix} f(x,y) \\ g(x,y) \end{bmatrix} = \vec{0} . \nonumber \]
En otras palabras, los puntos donde ambos\(f(x,y)=0\) and \(g(x,y)=0\).
Los puntos críticos son donde el comportamiento del sistema es en cierto sentido el más complicado. Si\(\left[ \begin{smallmatrix} f(x,y) \\ g(x,y) \end{smallmatrix} \right]\) is zero, then nearby, the vector can point in any direction whatsoever. Also, the trajectories are either going towards, away from, or around these points, so if we are looking for long term behavior of the system, we should look at what happens there.
A los puntos críticos también se les llama a veces equilibrios, ya que tenemos las llamadas soluciones de equilibrio en puntos críticos. Si\((x_0,y_0)\) is a critical point, then we have the solutions
\[x(t) = x_0, \quad y(t) = y_0 . \nonumber \]
En Ejemplo\(\PageIndex{1}\), there are two equilibrium solutions:
\[x(t) = 0, \quad y(t) = 0, \qquad \text{and} \qquad x(t) = 1, \quad y(t) = 0. \nonumber \]
Compare esta discusión sobre equilibrios con la discusión en la Sección 1.6. El concepto subyacente es exactamente el mismo.
Linealización
En la Sección 3.5 se estudió el comportamiento de un sistema lineal homogéneo de dos ecuaciones cerca de un punto crítico. Para un sistema lineal de dos variables el único punto crítico es generalmente el origen\((0,0)\). Let us put the understanding we gained in that section to good use understanding what happens near critical points of nonlinear systems.
En el cálculo aprendimos a estimar una función tomando su derivada y linealizando. Trabajamos de manera similar con sistemas no lineales de ODE. Supongamos\((x_0,y_0)\) is a critical point. First change variables to \((u,v)\), so that \((u,v)=(0,0)\) corresponds to \((x_0,y_0)\). That is,
\[u=x-x_0, \qquad v=y-y_0 . \nonumber \]
A continuación tenemos que encontrar el derivado. En el cálculo multivariable puede haber visto que la versión de varias variables de la derivada es la matriz jacobiana \(^{1}\). La matriz jacobiana de la función vectorizada\(\left[ \begin{smallmatrix} f(x,y) \\ g(x,y) \end{smallmatrix} \right]\) at \((x_0,y_0)\) is
\[ \begin{bmatrix}\frac{\partial f}{\partial x}(x_0,y_0) ~~~~ \frac{\partial f}{\partial y}(x_0,y_0) \\ \frac{\partial g}{\partial x}(x_0,y_0) ~~~~ \frac{\partial g}{\partial y}(x_0,y_0) \end{bmatrix} . \nonumber \]
Esta matriz da la mejor aproximación lineal\(u\) and \(v\) (and therefore \(x\) and \(y\)) vary. We define the linearization of the equation \(\eqref{eq:1}\) como el sistema lineal
\[ \begin{bmatrix} u \\ v \end{bmatrix} ' = \begin{bmatrix} \frac{\partial f}{\partial x}(x_0,y_0) ~~~ ~\frac{\partial f}{\partial y}(x_0,y_0) \\ \frac{\partial g}{\partial x}(x_0,y_0)~~~~ \frac{\partial g}{\partial y}(x_0,y_0) \end{bmatrix} \begin{bmatrix} u \\ v \end{bmatrix} . \nonumber \]
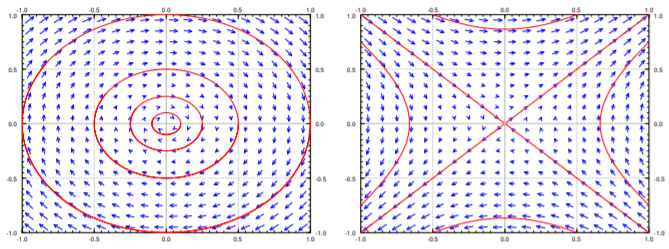
Sigamos con las mismas ecuaciones que Ejemplo\(\PageIndex{1}\): \(x' = y\), \(y' = -x+x^2\). There are two critical points, \((0,0)\)and \((1,0)\). The Jacobian matrix at any point is
\[\begin{bmatrix} \frac{\partial f}{\partial x}(x,y) ~~~~ \frac{\partial f}{\partial y}(x,y) \\ \frac{\partial g}{\partial x}(x,y) ~~~~ \frac{\partial g}{\partial y}(x,y) \end{bmatrix} = \begin{bmatrix} 0 & 1 \\ -1+2x & 0 \end{bmatrix}. \nonumber \]
Por lo tanto en\((0,0)\), we have \(u=x\) and \(v=y\), and the linearization is
\[\begin{bmatrix} u \\ v \end{bmatrix} ' =\begin{bmatrix}0 & 1 \\-1 & 0\end{bmatrix}\begin{bmatrix} u \\ v \end{bmatrix} , \nonumber \]
donde\(u=x\) and \(v=y\).
En el punto\((1,0)\), we have \(u=x-1\) and \(v=y\), and the linearization is
\[\begin{bmatrix} u \\ v \end{bmatrix} ' =\begin{bmatrix}0 & 1 \\1 & 0\end{bmatrix}\begin{bmatrix} u \\ v \end{bmatrix} . \nonumber \]
L a diagramas de fases de las dos linealizaciones en el punto\((0,0)\) and \((1,0)\) are given en Figura\(\PageIndex{3}\). Note that the variables are now \(u\) y\(v\). Comparar Figura\(\PageIndex{3}\) with Figure \(\PageIndex{2}\), and look especially at the behavior near the critical points.
Notas al pie
[1] Nombrado así por el matemático alemán Carl Gustav Jacob Jacobi (1804—1851).


