8.5: Caos
- Page ID
- 115471
Seguramente has escuchado la historia sobre el colgajo de un ala mariposa en la Amazonía causando huracanes en el Atlántico Norte. En una sección anterior, mencionamos que un pequeño cambio en las condiciones iniciales de los planetas puede conducir a una configuración muy diferente de los planetas a largo plazo. Estos son ejemplos de sistemas caóticos. El caos matemático no es realmente un caos, hay un orden preciso detrás de escena. Todo sigue siendo determinista. Sin embargo, un sistema caótico es extremadamente sensible a las condiciones iniciales. Esto también significa que incluso los pequeños errores inducidos a través de la aproximación numérica crean grandes errores muy rápidamente, por lo que es casi imposible aproximarse numéricamente durante largos tiempos. Esto es gran parte del problema ya que los sistemas caóticos no pueden resolverse en general analíticamente.
Toma el clima por ejemplo. Como un pequeño cambio en las condiciones iniciales (la temperatura en cada punto de la atmósfera, por ejemplo) produce predicciones drásticamente diferentes en un tiempo relativamente corto, no podemos predecir con precisión el clima. Esto se debe a que en realidad no conocemos las condiciones iniciales exactas, medimos temperaturas en algunos puntos con algún error y luego de alguna manera estimamos lo que hay en el medio. No hay manera de que podamos medir con precisión los efectos de cada ala de mariposa. Entonces resolveremos numéricamente introduciendo nuevos errores. Es por ello que no debes confiar en la predicción meteorológica más de unos días fuera.
La idea de comportamiento caótico fue notada por primera vez por Edward Lorenz en la década de 1960 al intentar modelar la convección (movimiento) de aire inducida térmicamente. Las ecuaciones que Lorentz estaba mirando desde el sistema de mirada relativamente simple:
\[ x' = -10x +10y, \quad y' = 28x-y-xz, \quad z'=-\frac{8}{3}z + xy . \nonumber \]
Un pequeño cambio en las condiciones iniciales produce una solución muy diferente después de un tiempo razonablemente corto.
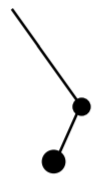
Un ejemplo muy sencillo con el que el lector puede experimentar, que muestra un comportamiento caótico, es un péndulo doble. Las ecuaciones que gobiernan este sistema son algo complicadas y su derivación es bastante tediosa, por lo que no vamos a molestarnos en escribirlas. La idea es poner un péndulo en el extremo de otro péndulo. Si nos fijamos en el movimiento de la masa inferior, el movimiento aparecerá caótico. Este tipo de sistema es una base para todo un número de juguetes de escritorio novedosos de oficina. Es muy sencillo construir una versión. Toma un trozo de cuerda, y ata dos tuercas pesadas en diferentes puntos de la cuerda; una al final, y otra un poco arriba. Ahora dale un pequeño empujón a la tuerca inferior, siempre y cuando los columpios no sean demasiado grandes y la cuerda se mantenga apretada, tienes un sistema de doble péndulo.
Ecuación de Duffing y atractores extraños
Estudiemos la llamada ecuación Duffing:
\[x'' + a x' + bx + cx^3 = C \cos(\omega t) . \nonumber \]
Aquí\(a\), \(b\), \(c\), \(C\), and \(\omega\) are constants. You will recognize that except for the \(c x^3\) term, this equation looks like a forced mass-spring system. The \(c x^3\) term comes up when the spring does not exactly obey Hooke's law (which no real-world spring actually does obey exactly). When \(c\) is not zero, the equation does not have a nice closed form solution, so we have to resort to numerical solutions as is usual for nonlinear systems. Not all choices of constants and initial conditions will exhibit chaotic behavior. Let us study
\[ x''+0.05 x' + x^3 = 8\cos(t) . \nonumber \]
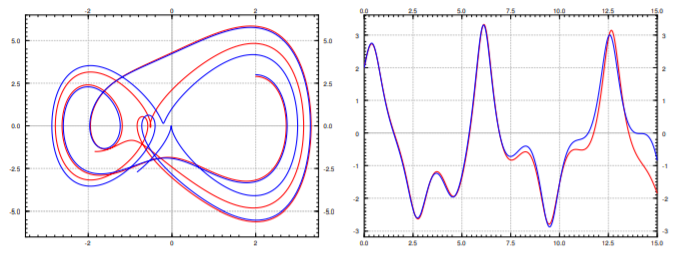
La ecuación no es autónoma, por lo que no podremos dibujar el campo vectorial en el plano de fase. Sin embargo, todavía podemos dibujar las trayectorias. En la Figura\(\PageIndex{2}\) we plot trajectories for \(t\) going from \(0\) to \(15\), for two very close initial conditions \((2,3)\) and \((2,2.9)\), and also the solutions in the \((x,t)\) space. The two trajectories are close at first, but after a while diverge significantly. This sensitivity to initial conditions is precisely what we mean by the system behaving chaotically.
Veamos el comportamiento a largo plazo. En la Figura\(\PageIndex{3}\), we plot the behavior of the system for initial conditions \((2,3)\), but for much longer period of time. Note that for this period of time it was necessary to use a ridiculously large number of steps\(^{1}\) in the numerical algorithm used to produce the graph, as even small errors quickly propagate. From the graph it is hard to see any particular pattern in the shape of the solution except that it seems to oscillate, but each oscillation appears quite unique. The oscillation is expected due to the forcing term.
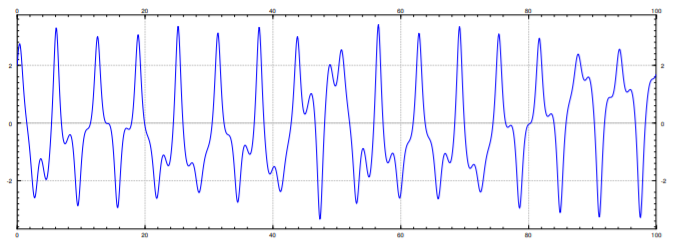
En general es muy difícil analizar sistemas caóticos, o encontrar el orden detrás de la locura, pero intentemos hacer algo que hicimos por el sistema estándar de masa-resorte. Una forma en que analizamos lo que sucede es que descubrimos cuál era el comportamiento a largo plazo (no dependiente de las condiciones iniciales). De la figura anterior queda claro que no vamos a obtener una buena descripción del comportamiento a largo plazo, pero quizás podamos averiguar algún orden a lo que sucede en cada “oscilación” y qué tienen en común estas oscilaciones.
El concepto que exploraremos es el de una sección Poincar é \(^{2}\). En lugar de mirar\(t\) in a certain interval, we will look at where the system is at a certain sequence of points in time. Imagine flashing a strobe at a certain fixed frequency and drawing the points where the solution is during the flashes. The right strobing frequency depends on the system in question. The correct frequency to use for the forced Duffing equation (and other similar systems) is the frequency of the forcing term. For the Duffing equation above, find a solution \(\bigl(x(t),y(t)\bigr)\), and look at the points
\[ \bigl(x(0),y(0)\bigr), \quad \bigl(x(2\pi),y(2\pi)\bigr), \quad \bigl(x(4\pi),y(4\pi)\bigr), \quad \bigl(x(6\pi),y(6\pi)\bigr), \quad \ldots \nonumber \]
Como realmente no nos interesa la parte transitoria de la solución, es decir, la parte de la solución que depende de la condición inicial saltamos algún número de pasos al principio. Por ejemplo, podríamos saltarnos los primeros 100 pasos de este tipo y comenzar a trazar puntos en\(t = 100(2\pi)\), that is
\[ \bigl(x(200\pi),y(200\pi)\bigr), \quad \bigl(x(202\pi),y(202\pi)\bigr), \quad \bigl(x(204\pi),y(204\pi)\bigr), \quad \bigl(x(206\pi),y(206\pi)\bigr), \quad \ldots \nonumber \]
La trama de estos puntos es la sección Poincaré. Después de trazar suficientes puntos, un curioso patrón emerge en la Figura\(\PageIndex{4}\) (the left hand picture), a so-called strange attractor.
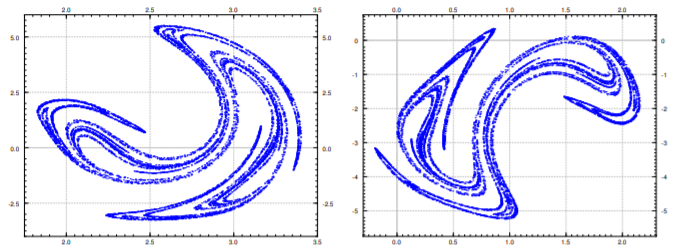
Si tenemos una secuencia de puntos, entonces un atractor es un conjunto hacia el que los puntos de la secuencia eventualmente se acercan cada vez más, es decir, se sienten atraídos. El apartado anterior de Poincaré no es realmente el atractor en sí, pero como los puntos están muy cerca de él, podemos ver su forma. El extraño atractor en la figura es un conjunto muy complicado, y de hecho tiene estructura fractal, es decir, si te acercarías hasta donde quieras, seguirías viendo la misma estructura complicada.
La condición inicial realmente no hace ninguna diferencia. Si empezáramos con diferente condición inicial, los puntos eventualmente gravitarían hacia el atractor, y así mientras tiramos los primeros puntos, siempre obtenemos la misma imagen.
Algo asombroso es que un sistema caótico como la ecuación Duffing no es nada aleatorio. Hay un orden muy complicado para ello, y el extraño atractor dice algo sobre este orden. No podemos decir exactamente en qué estado estará el sistema eventualmente, pero dada una frecuencia estroboscópica fija podemos estrecharlo a los puntos en el atractor.
Si usaras un cambio de fase, por ejemplo\(\frac{\pi}{4}\), and look at the times
\[\frac{\pi}{4}, \quad 2\pi+\frac{\pi}{4}, \quad 4\pi+\frac{\pi}{4}, \quad 6\pi+\frac{\pi}{4}, \quad \ldots \nonumber \]
se obtendría un atractor de aspecto ligeramente diferente. La imagen es el lado derecho de la Figura\(\PageIndex{4}\). It is as if we had rotated, distorted slightly, and then moved the original. Therefore for each phase shift you can find the set of points towards which the system periodically keeps coming back to.
Debes estudiar las imágenes y notar especialmente las escalas, donde se encuentran estos atractores en el plano de fase. Observe las regiones donde vive el extraño atractor y compárelo con la gráfica de las trayectorias en la Figura\(\PageIndex{2}\).
Comparemos la discusión en esta sección con la discusión en la Sección 2.6 sobre las oscilaciones forzadas. Toma la ecuación
\[ x''+2p x' + \omega_0^2 x = \frac{F_0}{m} \cos (\omega t) . \nonumber \]
Esto es como la ecuación Duffing, pero sin\(x^3\) term. The steady periodic solution is of the form
\[x = C \cos (\omega t + \gamma) . \nonumber \]
Strobing usando la frecuencia\(\omega\) we would obtain a single point in the phase space. So the attractor in this setting is a single point---an expected result as the system is not chaotic. In fact it was the opposite of chaotic. Any difference induced by the initial conditions dies away very quickly, and we settle into always the same steady periodic motion.
Sistema Lorenz
En dos dimensiones para tener el tipo de comportamiento caótico que estamos buscando, tenemos que estudiar sistemas forzados, o no autónomos, como la ecuación Duffing. Debido al Teorema de Poincar é -Bendoxson, si un sistema bidimensional autónomo tiene una solución que existe para siempre en el futuro y no va hacia el infinito, entonces obtenemos un ciclo límite o una trayectoria cerrada. Apenas el comportamiento caótico que estamos buscando.
En tres dimensiones incluso los sistemas autónomos pueden ser caóticos. Volvamos muy brevemente al sistema Lorenz
\[ x' = -10x +10y, \qquad y' = 28x-y-xz, \qquad z'=-\frac{8}{3}z + xy . \nonumber \]
El sistema Lorenz es un sistema autónomo en tres dimensiones que presenta un comportamiento caótico. Ver la Figura\(\PageIndex{5}\) for a sample trajectory, which is now a curve in three-dimensional space.
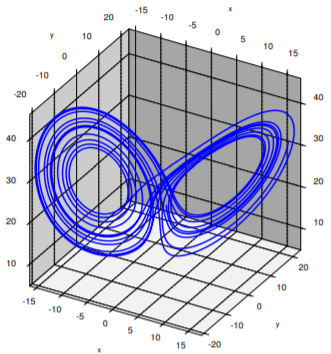
Las soluciones tenderán a un atractor en el espacio, el llamado atractor Lorenz. En este caso no es necesario ningún estroboscópico. Nuevamente no podemos ver del todo el atractor en sí, pero si tratamos de seguir una solución el tiempo suficiente, como en la figura, obtendremos una imagen bastante buena de cómo es el atractor. El atractor Lorenz también es un atractor extraño y tiene una estructura fractal complicada. Y, al igual que para la ecuación Duffing, lo que queremos dibujar no es toda la trayectoria, sino comenzar a dibujar la trayectoria después de un tiempo, una vez que esté cerca del atractor.
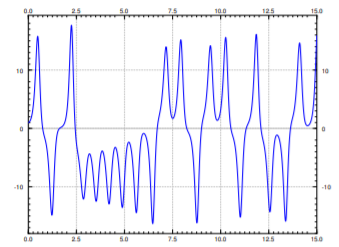
El camino no es sólo una repetición de ocho. La trayectoria girará un número aparentemente aleatorio de veces a la izquierda, luego girará varias veces a la derecha, y así sucesivamente. Como este sistema surgió en la predicción del clima, quizás uno pueda imaginar unos días de clima cálido y luego unos días de clima frío, donde no es fácil predecir cuándo cambiará el clima, así como no es realmente fácil predecir con mucha anticipación cuándo la solución saltará al otro lado. Ver Figura\(\PageIndex{6}\) for a plot of the \(x\) component of the solution drawn above. A negative \(x\) corresponds to the left "loop" and a positive \(x\) corresponds to the right "loop".
La mayor parte de las matemáticas que estudiamos en este libro es bastante clásica y bien entendida. Por otro lado, el caos, incluido el sistema Lorenz, sigue siendo objeto de investigación actual. Además, el caos ha encontrado aplicaciones no sólo en las ciencias, sino también en el arte.
Notas al pie
[1] De hecho, como referencia, se utilizaron 30,000 pasos con el algoritmo Runge—Kutta, ver ejercicios en la Sección 1.7.
[2] Nombrado así por el polímata francés Jules Henri Poincaré (1854-1912).


