8.4: Límite de ciclos
- Page ID
- 115453
Para los sistemas no lineales, las trayectorias no necesitan simplemente acercarse o dejar un solo punto. De hecho, pueden acercarse a un conjunto más grande, como un círculo u otra curva cerrada.
El oscilador Van der Pol \(^{1}\)es la siguiente ecuación
\[x''-\mu(1-x^2) x' + x = 0, \nonumber \]
donde\(\mu\) is some positive constant. The Van der Pol oscillator originated with electrical circuits, but finds applications in diverse fields such as biology, seismology, and other physical sciences.
Para simplificar, usemos\(\mu = 1\). A phase diagram is given in the left hand plot in Figure \(\PageIndex{1}\). Notice how the trajectories seem to very quickly settle on a closed curve. On the right hand plot we have the plot of a single solution for \(t=0\) to \(t=30\) with initial conditions \(x(0) = 0.1\) and \(x'(0) = 0.1\). Notice how the solution quickly tends to a periodic solution.
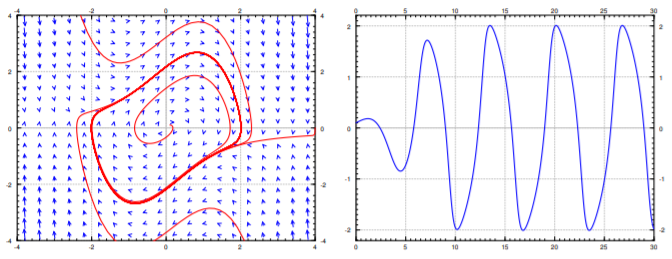
El oscilador Van der Pol es un ejemplo de la llamada oscilación de relajación. La palabra relajación viene del salto repentino (la parte muy empinada de la solución). Para mayores\(\mu\) the steep part becomes even more pronounced, for small \(\mu\) the limit cycle looks more like a circle. In fact setting \(\mu = 0\), we get \(x''+x=0\), which is a linear system with a center and all trajectories become circles.
La curva cerrada en el retrato de fase anterior se denomina ciclo límite. Un ciclo límite es una trayectoria cerrada de tal manera que al menos otra trayectoria gira en espiral dentro de ella (o espirales fuera de ella). Si todas las trayectorias que comienzan cerca del ciclo límite espiral en él, el ciclo límite se denomina asintóticamente estable. El ciclo límite en el oscilador Van der Pol es asintóticamente estable.
Dado un ciclo límite en un sistema autónomo, cualquier solución que se inicie en él es periódica. De hecho, esto es cierto para cualquier trayectoria que sea una curva cerrada (una llamada trayectoria cerrada). Tal curva se llama órbita periódica. Más precisamente, si\(\bigl(x(t),y(t)\bigr)\) is a solution such that for some \(t_0\) the point \(\bigl(x(t_0),y(t_0)\bigr)\) lies on a periodic orbit, then both \(x(t)\) and \(y(t)\) are periodic functions (with the same period). That is, there is some number \(P\) such that \(x(t) = x(t+P)\) and \(y(t) = y(t+P)\).
Considerar el sistema
\[\label{eq:2} x' = f(x,y), ~~~~~ y' = g(x,y) , \]
donde las funciones\(f\) and \(g\) have continuous derivatives in some region \(R\) in the plane.
Supongamos\(R\) is a closed bounded region (a region in the plane that includes its boundary and does not have points arbitrarily far from the origin). Suppose \(\bigl(x(t), y(t)\bigr)\) is a solution of \(\eqref{eq:2}\) in \(R\) that exists for all \(t \geq t_0\). Then either the solution is a periodic function, or the solution spirals towards a periodic solution in \(R\).
El punto principal del teorema es que si encuentras una solución que existe para todos lo suficientemente\(t\) grande (es decir, como\(t\) va al infinito) y se mantiene dentro de una región acotada, entonces has encontrado ya sea una órbita periódica, o una solución que gira en espiral hacia un ciclo límite o tiende a un punto crítico. Es decir, a largo plazo, el comportamiento es muy cercano a una función periódica. Tenga en cuenta que una solución constante en un punto crítico es periódica (con cualquier período). El teorema es más una afirmación cualitativa más que algo que nos ayude en los cálculos. En la práctica es difícil encontrar soluciones analíticas y tan difícil demostrar rigurosamente que existen para siempre. Pero si pensamos que la solución existe resolvemos numéricamente durante mucho tiempo para aproximarnos al ciclo límite. Otra advertencia es que el teorema sólo funciona en dos dimensiones. En tres dimensiones y superiores, simplemente hay demasiado espacio.
El teorema se aplica a todas las soluciones en el oscilador Van der Pol. Las soluciones que comienzan en cualquier punto excepto el origen\((0,0)\) tenderán a la solución periódica alrededor del ciclo límite, y si la condición inicial de\((0,0)\) conducirá a la solución constante\(x=0\),\(y=0\).
Considere\[x' = y + {(x^2+y^2-1)}^2 x, \qquad y' = -x + {(x^2+y^2-1)}^2 y. \nonumber \] un campo vectorial junto con soluciones con condiciones iniciales\((1.02,0)\),\((0.9,0)\), y\((0.1,0)\) se dibujan en la Figura\(\PageIndex{2}\).
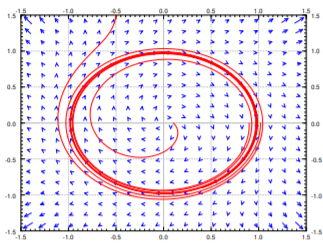
Observe que los puntos en el círculo unitario (distancia uno del origen) satisfacen\(x^2+y^2-1=0\). Y\(x(t) = \sin(t)\),\(y = \cos(t)\) es una solución del sistema. Por lo tanto tenemos una trayectoria cerrada. Para los puntos fuera del círculo unitario, el segundo término en\(x'\) empuja la solución más lejos del\(y\) eje -que del sistema\(x' = y\)\(y' = -x\),, y\(y'\) empuja la solución más lejos del\(x\) eje -que del sistema lineal\(x'=y\),\(y' = -x\). En otras palabras, para todas las demás condiciones iniciales la trayectoria saldrá en espiral.
Esto significa que para las condiciones iniciales dentro del círculo unitario, la solución gira hacia la solución periódica en el círculo unitario, y para las condiciones iniciales fuera del círculo unitario, las soluciones giran hacia el infinito. Por lo tanto, el círculo unitario es un ciclo límite, pero no asintóticamente estable. El Teorema de Poincaré-Bendixson se aplica a los puntos iniciales dentro del círculo unitario, ya que esas soluciones permanecen delimitadas, pero no a las de afuera, ya que esas soluciones van al infinito.
Un análisis muy similar se aplica al sistema Todavía\[x' = y + {(x^2+y^2-1)} x, \qquad y' = -x + {(x^2+y^2-1)} y. \nonumber \] obtenemos una trayectoria cerrada en el círculo unitario, y los puntos fuera del círculo unitario espiral hacia el infinito, pero ahora apunta dentro del círculo unitario espiral hacia el punto crítico en el origen. Por lo que este sistema no tiene un ciclo límite, a pesar de que tiene una trayectoria cerrada.
Debido al teorema de Picard (3.1.1) encontramos que no importa dónde nos encontremos en el plano siempre podemos encontrar una solución un poco más allá en el tiempo, siempre\(f\) y cuando\(g\) tengamos derivadas continuas. Entonces, si encontramos una trayectoria cerrada en un sistema autónomo, entonces por cada punto inicial dentro de la trayectoria cerrada, la solución existirá para siempre y permanecerá delimitada (permanecerá dentro de la trayectoria cerrada). Entonces, en el momento en que encontramos la solución anterior dando la vuelta al círculo unitario, sabíamos que por cada punto inicial dentro del círculo, la solución existe para siempre y se aplica el teorema de Poincaré—Bendixson.
Busquemos a continuación las condiciones en las que no existan ciclos límite (u órbitas periódicas). Suponemos que la ecuación\(\eqref{eq:2}\) se define en una región simplemente conectada, es decir, una región sin agujeros que podamos rodear. Por ejemplo, todo el plano es una región simplemente conectada, y también lo es el interior del disco de la unidad. Sin embargo, todo el plano menos un punto no es un dominio simplemente conectado ya que tiene un en el origen.
Supongamos\(f\) and \(g\) are defined in a simply connected region \(R\). If the expression\(^{4}\)
\[ \frac{\partial f}{\partial x} + \frac{\partial g}{\partial y} \nonumber \]
es siempre positivo o siempre negativo en\(R\) (except perhaps a small set such as on isolated points or curves) then the system \(\eqref{eq:2}\) has no closed trajectory inside \(R\).
El teorema nos da una manera de descartar la existencia de una trayectoria cerrada, y de ahí una manera de descartar ciclos límite. La excepción sobre puntos o líneas realmente significa que podemos permitir que la expresión sea cero en unos pocos puntos, o tal vez en una curva, pero no en cualquier conjunto mayor.
Echemos un vistazo a\(x'=y+y^2e^x\), \(y'=x\) in the entire plane (see Example 8.2.2.) The entire plane is simply connected and so we can apply the theorem. We compute \(\frac{\partial f}{\partial x} + \frac{\partial g}{\partial y} = y^2e^x+ 0\). The function \(y^2e^x\) is always positive except on the line \(y=0\). Therefore, via the theorem, the system has no closed trajectories.
En algunos libros (o internet) el teorema no se afirma con cuidado y concluye que no hay soluciones periódicas. Eso no es del todo correcto. El ejemplo anterior tiene dos puntos críticos y por lo tanto tiene soluciones constantes, y las funciones constantes son periódicas. La conclusión del teorema debe ser que no existen trayectorias que formen curvas cerradas. Otra forma de afirmar la conclusión del teorema sería decir que no existen soluciones periódicas inconstantes que permanezcan en\(R\).
Veamos un ejemplo algo más complicado. Toma el sistema\(x'=-y-x^2\), \(y'=-x+y^2\) (see Example 8.2.1). We compute \(\frac{\partial f}{\partial x} + \frac{\partial g}{\partial y} = 2x + 2y\). This expression takes on both signs, so if we are talking about the whole plane we cannot simply apply the theorem. However, we could apply it on the set where \(x+y > 0\). Via the theorem, there is no closed trajectory in that set. Similarly, there is no closed trajectory in the set \(x+y < 0\). We cannot conclude (yet) that there is no closed trajectory in the entire plane. Perhaps half of it is in the set where \(x+y >0\) and the other half is in the set where \(x+y < 0\).
La clave es mirar el conjunto\(x+y=0\), or \(x=-y\). Let us make a substitution \(x=z\) and \(y=-z\) (so that \(x=-y\)). Both equations become \(z'=z-z^2\). So any solution of \(z'=z-z^2\), gives us a solution \(x(t)=z(t)\), \(y(t)=-z(t)\). In particular, any solution that starts out on the line \(x+y=0\), stays on the line \(x+y = 0\). In other words, there cannot be a closed trajectory that starts on the set where \(x+y > 0\) and goes through the set where \(x+y < 0\), as it would have to pass through \(x+y = 0\).
Considerar\(x' = y+(x^2+y^2-1)x\)\(y' = -x +(x^2+y^2-1)y\),, y considerar la región\(R\) dada por\(x^2+y^2 > \frac{1}{2}\). Es decir,\(R\) es la región fuera de un círculo de radio\(\frac{1}{\sqrt{2}}\) centrado en el origen. Entonces hay una trayectoria cerrada en\(R\), es decir\(x=\cos(t)\),\(y=\sin(t)\). Además,\[\frac{\partial f}{\partial x} + \frac{\partial g}{\partial x} = 4x^2+4y^2-2 , \nonumber \] lo que siempre es positivo en\(R\). Entonces, ¿qué está pasando? El teorema de Bendixson—Dulac no se aplica ya que la región no\(R\) está simplemente conectada— ¡tiene un agujero, el círculo que cortamos!
Notas al pie
[1] Nombrado así por el físico holandés Balthasar van der Pol (1889—1959).
[2] Ivar Otto Bendixson (1861-1935) fue un matemático sueco.
[3] Henri Dulac (1870—1955) fue un matemático francés.
[4] Por lo general, la expresión en el Teorema de Bendixson—Dulac es\(\frac{\partial (\varphi f)}{\partial x}+\frac{\partial (\varphi g)}{\varphi y}\) para alguna función continuamente diferenciable\(\varphi\). Por simplicidad, consideremos el caso\(\varphi =1\).


