1.2: Conceptos básicos
- Page ID
- 114593
Una ecuación diferencial es una ecuación que contiene una o más derivadas de una función desconocida. El orden de una ecuación diferencial es el orden de la derivada más alta que contiene. Una ecuación diferencial es una ecuación diferencial ordinaria si involucra una función desconocida de una sola variable, o una ecuación diferencial parcial si involucra derivadas parciales de una función de más de una variable. Por ahora consideraremos solo ecuaciones diferenciales ordinarias, y solo las llamaremos ecuaciones diferenciales.
A lo largo de este texto, todas las variables y constantes son reales a menos que se indique lo contrario. Usualmente usaremos\(x\) para la variable independiente a menos que la variable independiente sea tiempo; luego usaremos\(t\).
Las ecuaciones diferenciales más simples son ecuaciones de primer orden de la forma
\[{dy\over dx}=f(x) \nonumber\]
o equivalentemente
\[y'=f(x), \nonumber\]
donde\(f\) es una función conocida de\(x\). Ya sabemos por cálculo cómo encontrar funciones que satisfagan este tipo de ecuaciones. Por ejemplo, si
\[y'=x^3, \nonumber\]
entonces
\[y=\int x^3\, dx={x^4\over4}+c, \nonumber\]
donde\(c\) es una constante arbitraria. Si\(n>1\) podemos encontrar funciones\(y\) que satisfagan ecuaciones de la forma
\[\label{eq:1.2.1} y^{(n)}=f(x)\]
por integración repetida. Nuevamente, este es un problema de cálculo.
Excepto para fines ilustrativos en esta sección, no hay necesidad de considerar ecuaciones diferenciales como la Ecuación\ ref {eq:1.2.1}. Por lo general, consideraremos ecuaciones diferenciales que se pueden escribir como
\[\label{eq:1.2.2} y^{(n)}=f(x,y,y', \dots,y^{(n-1)}),\]
donde al menos una de las funciones\(y\),\(y'\),..., en\(y^{(n-1)}\) realidad aparece a la derecha. Aquí hay algunos ejemplos:
\ begin {array} {rcll} {dy\ over dx} -x^2&=&0&\ mbox {(primer pedido)},\\ {dy\ over dx} +2xy^2&=&-2&\ mbox {(primer pedido)},\\ {d^2y\ sobre dx^2} +2 {dy\ over dx} +y&=&2x&\ mbox {(segundo pedido)},\\ xy"'+y^2&=&\ sin x &\ mbox {(tercer orden)},\\ y^ {(n)} +xy'+3y&=&x&\ mbox { (orden n)}. \ nonumber\ end {array}
Aunque ninguna de estas ecuaciones está escrita como en la Ecuación\ ref {eq:1.2.2}, todas ellas pueden escribirse de esta forma:
\[\begin{array}{rcl} y'&=&x^2, \\ y'&=&-2-2xy^2, \\ y''&=&2x-2y'-y, \\ y'''&=& \dfrac{\sin x-y^2}{x}, \\[4pt] y^{(n)}&=&x-xy'-3y. \end{array}\nonumber \]
Soluciones de Ecuaciones Diferenciales
Una solución de una ecuación diferencial es una función que satisface la ecuación diferencial en algún intervalo abierto; así,\(y\) es una solución de la Ecuación\ ref {eq:1.2.2} si\(y\) es\(n\) tiempos diferenciables y
\[y^{(n)}(x)=f(x,y(x),y'(x), \dots,y^{(n-1)}(x)) \nonumber\]
para todos\(x\) en algún intervalo abierto\((a,b)\). En este caso, también decimos que\(y\) es una solución o f Ecuación\ ref {eq:1.2.2} o n\((a,b)\). Las funciones que satisfacen una ecuación diferencial en puntos aislados no son interesantes. Por ejemplo,\(y=x^2\) satisface
\[xy'+x^2=3x \nonumber\]
si y sólo si\(x=0\) o\(x=1\), pero no es una solución de esta ecuación diferencial porque no satisface la ecuación en un intervalo abierto.
La gráfica de una solución de una ecuación diferencial es una curva de solución. De manera más general,\(C\) se dice que una curva es una curva integral de una ecuación diferencial si cada función\(y=y(x)\) cuya gráfica es un segmento de\(C\) es una solución de la ecuación diferencial. Por lo tanto, cualquier curva de solución de una ecuación diferencial es una curva integral, pero una curva integral no necesita ser una curva de solución.
Si\(a\) hay alguna constante positiva, el círculo
\[\label{eq:1.2.3} x^2+y^2=a^2\]
es una curva integral de
\[\label{eq:1.2.4} y'=-{x\over y}.\]
Solución
Para ver esto, tenga en cuenta que las únicas funciones cuyas gráficas son segmentos de Ecuación\ ref {eq:1.2.3} son
\[y_1=\sqrt{a^2-x^2} \quad \text{and} \quad y_2=-\sqrt{a^2-x^2}.\nonumber \]
Te dejamos verificar que estas funciones satisfacen ambas Ecuación\ ref {eq:1.2.4} en el intervalo abierto\((-a,a)\). Sin embargo, la Ecuación\ ref {eq:1.2.3} no es una curva de solución de la Ecuación\ ref {eq:1.2.4}, ya que no es la gráfica de una función.
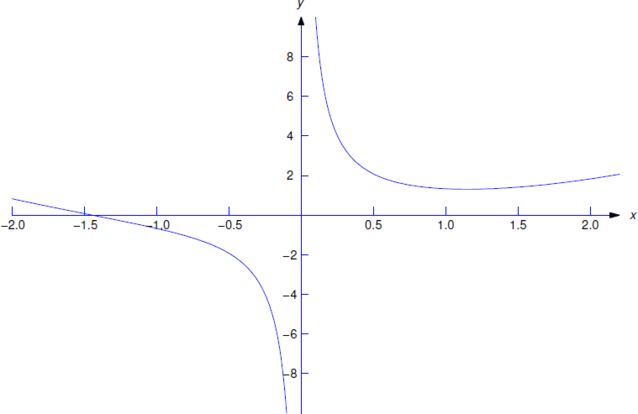
Verifica que
\[\label{eq:1.2.5} y={x^2\over3}+{1\over x}\]
es una solución de
\[\label{eq:1.2.6} xy'+y=x^2\]
encendido\((0,\infty)\) y encendido\((-\infty,0)\).
Solución
Ecuación sustitutiva\ ref {eq:1.2.5} y
\[y'={2x\over3} - {1\over x^2}\nonumber \]
en Ecuación\ ref {eq:1.2.6} rendimientos
\[xy'(x)+y(x)=x \left({2x\over3} - {1\over x^2}\right)+ \left({x^2\over3}+{1\over x}\right)=x^2\nonumber \]
para todos\(x\ne0\). Por lo tanto\(y\) es una solución de Ecuación\ ref {eq:1.2.6} on\((-\infty,0)\) y\((0,\infty)\). Sin embargo,\(y\) no es una solución de la ecuación diferencial en ningún intervalo abierto que contenga\(x=0\), ya que no\(y\) se define en\(x=0\).
La Figura 1.2.2 muestra la gráfica de la Ecuación\ ref {eq:1.2.5}. La parte de la gráfica de la Ecuación\ ref {eq:1.2.5} on\((0,\infty)\) es una curva de solución de la Ecuación\ ref {eq:1.2.6}, como es la parte de la gráfica sobre\((-\infty,0)\).
Mostrar que si\(c_1\) y\(c_2\) son constantes entonces
\[\label{eq:1.2.7} y=(c_1+c_2x)e^{-x}+2x-4\]
es una solución de\[\label{eq:1.2.8} y''+2y'+y=2x\] on\((-\infty,\infty)\).
Solución
Ecuación diferenciadora\ ref {eq:1.2.7} rendimientos dos veces
\[y'=-(c_1+c_2x)e^{-x}+c_2e^{-x}+2 \nonumber\]
y
\[y''=(c_1+c_2x)e^{-x}-2c_2e^{-x}, \nonumber\]
por lo
\[\begin{align*} y''+2y'+y&=(c_1+c_2x)e^{-x}-2c_2e^{-x} + 2\left[-(c_1+c_2x)e^{-x}+c_2e^{-x}+2\right] +(c_1+c_2x)e^{-x}+2x-4 \\[4pt] &=(1-2+1)(c_1+c_2x)e^{-x}+(-2+2)c_2e^{-x} + 4+2x-4 \\[4pt] &=2x \end{align*}\]
para todos los valores de\(x\). Por lo tanto\(y\) es una solución de la Ecuación\ ref {eq:1.2.8} on\((-\infty,\infty)\).
Encuentra todas las soluciones de
\[\label{eq:1.2.9} y^{(n)}=e^{2x}.\]
Solución
Ecuación de integración\ ref {eq:1.2.9} rendimientos
\[y^{(n-1)}={e^{2x}\over2}+k_1, \nonumber\]
donde\(k_1\) es una constante. Si\(n\ge2\), integrando de nuevo los rendimientos
\[y^{(n-2)}={e^{2x}\over4}+k_1x+k_2. \nonumber\]
Si\(n\ge3\), integrando repetidamente rendimientos
\[\label{eq:1.2.10} y={e^{2x}\over2^n}+k_1{x^{n-1}\over (n-1)!}+k_2{x^{n-2}\over (n-2)!}+\cdots+k_n,\]
donde\(k_1\),\(k_2\),...,\(k_n\) son constantes. Esto demuestra que cada solución de la Ecuación\ ref {eq:1.2.9} tiene la forma Ecuación\ ref {eq:1.2.10} para alguna elección de las constantes\(k_1\),\(k_2\),...,\(k_n\). Por otro lado, diferenciar la Ecuación\ ref {eq:1.2.10}\(n\) tiempos muestra que si\(k_1\),,...\(k_2\),\(k_n\) son constantes arbitrarias, entonces la función\(y\) en la Ecuación\ ref {eq:1.2.10} satisface la Ecuación\ ref {eq:1.2.9}.
Dado que las constantes\(k_1\),\(k_2\),...,\(k_n\) en la Ecuación\ ref {eq:1.2.10} son arbitrarias, también lo son las constantes
\[{k_1\over (n-1)!},\, {k_2\over(n-2)!},\, \cdots, \, k_n. \nonumber\]
Por lo tanto, el ejemplo 1.2.4 realmente muestra que todas las soluciones de la ecuación\ ref {eq:1.2.9} se pueden escribir como
\[y={e^{2x}\over2^n}+c_1+c_2x+\cdots+c_nx^{n-1}, \nonumber\]
donde renombramos las constantes arbitrarias en la Ecuación\ ref {eq:1.2.10} para obtener una fórmula más simple. Como regla general, las constantes arbitrarias que aparecen en las soluciones de ecuaciones diferenciales deben simplificarse si es posible. Verás ejemplos de esto a lo largo del texto.
Problemas de Valor Inicial
En Example 1.2.4 vimos que la ecuación diferencial\(y^{(n)}=e^{2x}\) tiene una familia infinita de soluciones que dependen de las constantes\(n\) arbitrarias\(c_1\),\(c_2\),...,\(c_n\). A falta de condiciones adicionales, no hay razón para preferir una solución de una ecuación diferencial sobre otra. Sin embargo, a menudo nos interesará encontrar una solución de una ecuación diferencial que satisfaga una o más condiciones específicas. El siguiente ejemplo ilustra esto.
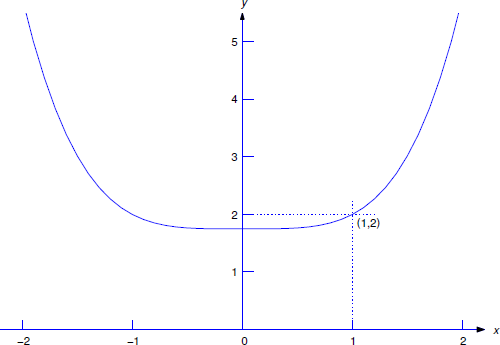
Encuentra una solución de\[y'=x^3 \nonumber\] tal que\(y(1)=2\).
Solución
Al inicio de esta sección vimos que las soluciones de\(y'=x^3\) son
\[y={x^4\over4}+c. \nonumber\]
Para determinar un valor de\(c\) tal que\(y(1)=2\), establecemos\(x=1\) y\(y=2\) aquí para obtener
\[2=y(1)={1\over4}+c \nonumber\]
por lo
\[c={7\over4}. \nonumber\]
Por lo tanto, la solución requerida es
\[y={x^4+7\over4}. \nonumber\]
La figura 1.2.2 muestra la gráfica de esta solución. Tenga en cuenta que imponer la condición\(y(1)=2\) equivale a requerir que la gráfica de\(y\) pase por el punto\((1,2)\).
Podemos reescribir el problema considerado en Ejemplo 1.2.5 más brevemente como
\[y'=x^3,\quad y(1)=2.\nonumber\]
A esto lo llamamos un problema de valor inicial. El requisito\(y(1)=2\) es una condición inicial. También se pueden plantear problemas de valor inicial para ecuaciones diferenciales de orden superior. Por ejemplo,
\[\label{eq:1.2.11} y'' - 2y'+3y=e^x, \quad y(0)=1, \quad y'(0)=2\]
es un problema de valor inicial para una ecuación diferencial de segundo orden donde\(y\) y\(y'\) se requiere que tengan valores especificados en\(x=0\). En general, un problema de valor inicial para una ecuación diferencial de orden\(n\) -ésimo requiere\(y\) que sus primeras\(n-1\) derivadas tengan valores especificados en algún momento\(x_0\). Estos requisitos son las condiciones iniciales. Denotaremos un problema de valor inicial para una ecuación diferencial escribiendo las condiciones iniciales después de la ecuación, como en la Ecuación\ ref {eq:1.2.11}. Por ejemplo, escribiríamos un problema de valor inicial para la ecuación\ ref {eq:1.2.2} como
\[\label{eq:1.2.12} y^{(n)}=f(x,y,y', \dots,y^{(n-1)}),\, y(x_0)=k_0,\, y'(x_0)=k_1,\, \dots,\, y^{(n-1)}=k_{n-1}.\]
Consistente con nuestra definición anterior de una solución de la ecuación diferencial en la Ecuación\ ref {eq:1.2.12}, decimos que\(y\) es una solución del problema del valor inicial Ecuación\ ref {eq:1.2.12} si\(y\) es\(n\) tiempos diferenciables y
\[y^{(n)}(x)=f(x,y(x),y'(x), \dots,y^{(n-1)}(x))\nonumber\]
para todos\(x\) en algún intervalo abierto\((a,b)\) que contiene\(x_0\), y\(y\) satisface las condiciones iniciales en la Ecuación\ ref {eq:1.2.12}. El intervalo abierto más grande que contiene\(x_0\) sobre el que\(y\) se define y satisface la ecuación diferencial es el intervalo de validez de\(y\).
En Ejemplo 1.2.5 vimos que
\[\label{eq:1.2.13} y={x^4+7\over4}\]
es una solución del problema de valor inicial
\[y'=x^3,\quad y(1)=2.\nonumber\]
Dado que la función en la Ecuación\ ref {eq:1.2.13} está definida para todos\(x\), el intervalo de validez de esta solución es\((-\infty,\infty)\).
En Ejemplo 1.2.2 verificamos que
\[\label{eq:1.2.14} y={x^2\over3}+{1\over x}\]
es una solución de
\[xy'+y=x^2 \nonumber\]
encendido\((0,\infty)\) y encendido\((-\infty,0)\). Al evaluar la ecuación\ ref {eq:1.2.14} at\(x=\pm1\), se puede ver que la ecuación\ ref {eq:1.2.14} es una solución de los problemas de valor inicial
\[\label{eq:1.2.15} xy'+y=x^2,\quad y(1)={4\over3}\]
y
\[\label{eq:1.2.16} xy'+y=x^2,\quad y(-1)=-{2\over3}.\]
El intervalo de validez de la Ecuación\ ref {eq:1.2.14} como solución de la Ecuación\ ref {eq:1.2.15} es\((0,\infty)\), ya que este es el intervalo más grande que contiene\(x_0=1\) sobre qué Ecuación\ ref {eq:1.2.14} se define. De igual manera, el intervalo de validez de la Ecuación\ ref {eq:1.2.14} como solución de la Ecuación\ ref {eq:1.2.16} es\((-\infty,0)\), ya que este es el intervalo más grande que contiene\(x_0=-1\) sobre qué Ecuación\ ref {eq:1.2.14} se define.
Caída Libre Bajo Gravedad Constante
El término problema de valor inicial se originó en problemas de movimiento donde la variable independiente es\(t\) (que representa el tiempo transcurrido), y las condiciones iniciales son la posición y velocidad de un objeto en el tiempo inicial (inicio) de un experimento.
Un objeto cae bajo la influencia de la gravedad cerca de la superficie de la Tierra, donde se puede suponer que la magnitud de la aceleración debida a la gravedad es una constante\(g\).
- Construir un modelo matemático para el movimiento del objeto en forma de problema de valor inicial para una ecuación diferencial de segundo orden, asumiendo que\(t=0\) se conocen la altitud y velocidad del objeto en el momento. Supongamos que la gravedad es la única fuerza que actúa sobre el objeto.
- Resolver el problema de valor inicial derivado anteriormente para obtener la altitud en función del tiempo.
Solución a
Dejar\(y(t)\) ser la altitud del objeto en el momento\(t\). Dado que la aceleración del objeto tiene magnitud constante\(g\) y está en dirección descendente (negativa),\(y\) satisface la ecuación de segundo orden
\[y''=-g, \nonumber\]
donde el primo ahora indica diferenciación con respecto a\(t\). Si\(y_0\) y\(v_0\) denotan la altitud y velocidad cuando\(t=0\), entonces\(y\) es una solución del problema de valor inicial
\[\label{eq:1.2.17} y''=-g,\quad y(0)=y_0,\quad y'(0)=v_0.\]
Solución b
Ecuación de integración\ ref {eq:1.2.17} rendimientos dos veces
\[\begin{aligned} y'&=-gt+c_1, \\ y&=-{gt^2\over2}+c_1t+c_2.\end{aligned}\]
La imposición de las condiciones iniciales\(y(0)=y_0\) y\(y'(0)=v_0\) en estas dos ecuaciones muestra que\(c_1=v_0\) y\(c_2=y_0\). Por lo tanto, la solución del problema del valor inicial Ecuación\ ref {eq:1.2.17} es
\[y=- {gt^2\over2}+v_0t+y_0. \nonumber\]


