1.3: Campos de dirección para ecuaciones de primer orden

Es imposible encontrar fórmulas explícitas para soluciones de algunas ecuaciones diferenciales. Aunque existan tales fórmulas, pueden ser tan complicadas que son inútiles. En este caso podemos recurrir a métodos gráficos o numéricos para hacernos una idea de cómo se comportan las soluciones de la ecuación dada.

En la Sección 2.3 abordaremos la cuestión de la existencia de soluciones de una ecuación de primer orden\[\label{eq:1.3.1} y'=f(x,y).\]

En esta sección simplemente asumiremos que la Ecuación\ ref {eq:1.3.1} tiene soluciones y discutiremos un método gráfico para aproximarlas. En el Capítulo 3 discutimos métodos numéricos para obtener soluciones aproximadas de la Ecuación\ ref {eq:1.3.1}. Recordemos que una solución de Ecuación\ ref {eq:1.3.1} es una función\(y=y(x)\) tal que

\[y'(x)=f(x,y(x))\nonumber \]

para todos los valores de\(x\) en algún intervalo, y una curva integral es o bien la gráfica de una solución o se compone de segmentos que son gráficas de soluciones. Por lo tanto, no poder resolver la Ecuación\ ref {eq:1.3.1} equivale a no conocer las ecuaciones de curvas integrales de la Ecuación\ ref {eq:1.3.1}. Sin embargo, es fácil calcular las pendientes de estas curvas. Para ser específicos, la pendiente de una curva integral de la Ecuación\ ref {eq:1.3.1} a través de un punto dado\((x_0,y_0)\) viene dada por el número\(f(x_0,y_0)\). Esta es la base del método de campos de dirección.

Si\(f\) se define en un conjunto\(R\), podemos construir un campo de dirección para Ecuación\ ref {eq:1.3.1} in\(R\) dibujando un segmento de línea corta a través de cada punto\((x,y)\) en\(R\) con pendiente\(f(x,y)\). Por supuesto, como cuestión práctica, en realidad no podemos dibujar segmentos de línea a través de cada punto en\(R\); más bien, debemos seleccionar un conjunto finito de puntos en\(R\). Por ejemplo, supongamos que\(f\) se define en la región rectangular cerrada\[R:\{a\le x\le b, c\le y\le d\}.\nonumber \]

Dejar\[a= x_0< x_1< \cdots< x_m=b\nonumber \] ser puntos igualmente espaciados en\([a,b]\) y\[c=y_{0}<y_{1}<\cdots < y_{n}=d\nonumber \]formar uncuadrícula rectangular (Figura 1.3.1 ). A través de cada punto de la rejilla dibujamos un segmento de línea corto con pendiente\(f(x_i,y_j)\). El resultado es una aproximación a un campo de dirección para Ecuación\ ref {eq:1.3.1} pulg\(R\). Si los puntos de la cuadrícula son suficientemente numerosos y están muy próximos entre sí, podemos dibujar curvas integrales aproximadas de la Ecuación\ ref {eq:1.3.1} dibujando curvas a través de puntos en la cuadrícula tangentes a los segmentos de línea asociados con los puntos en la cuadrícula.

Figura 1.3.1 : Una cuadrícula rectangular

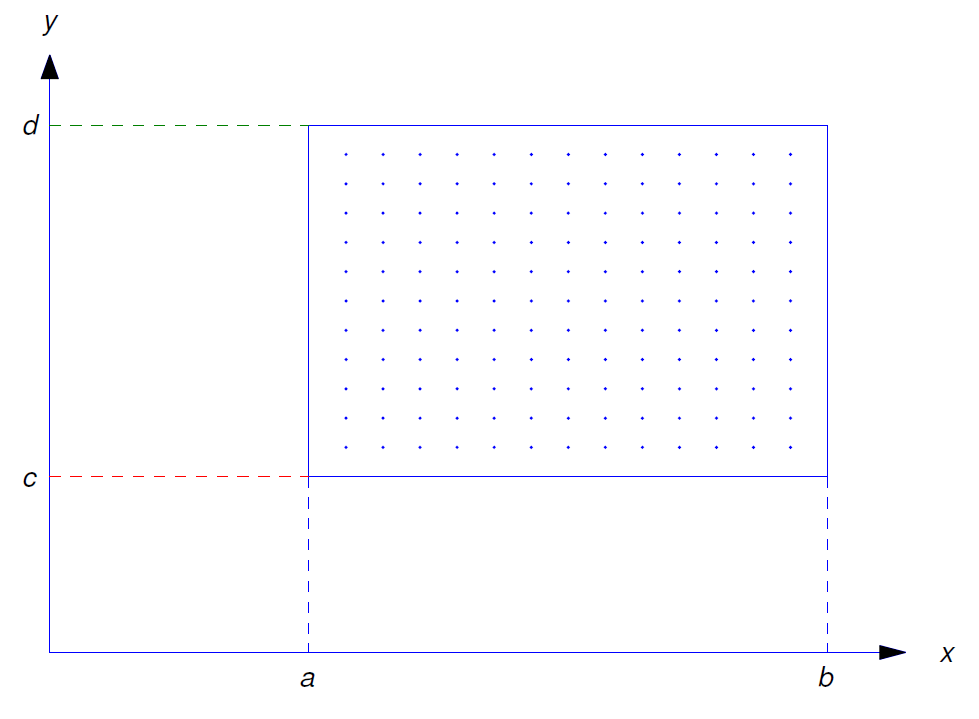
Desafortunadamente, aproximar un campo de dirección y graficar curvas integrales de esta manera es demasiado tedioso para hacerse de manera efectiva a mano. No obstante, hay software para hacer esto. Como verá, la combinación de campos de dirección y curvas integrales brinda información útil sobre el comportamiento de las soluciones de la ecuación diferencial incluso si no podemos obtener soluciones exactas.

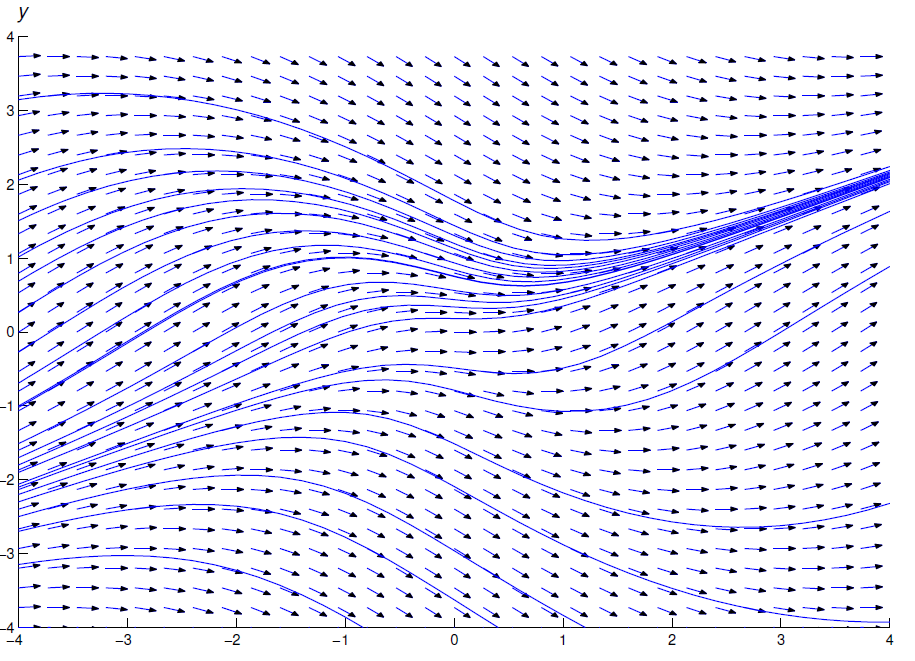
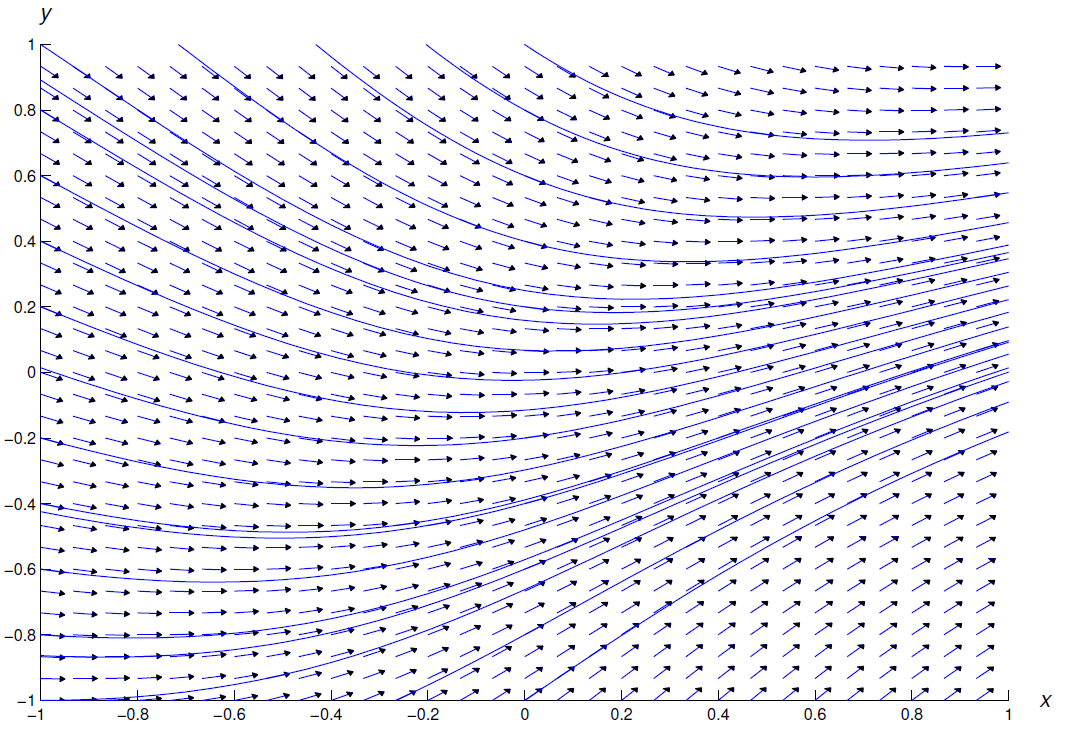
Estudiaremos métodos numéricos para resolver una sola ecuación de primer orden Ecuación\ ref {eq:1.3.1} en el Capítulo 3. Estos métodos se pueden utilizar para trazar curvas de solución de la Ecuación\ ref {eq:1.3.1} en una región rectangular\(R\) si\(f\) es continua en\(R\). Las figuras 1.3.2 , 1.3.3 y 1.3.4 muestran campos de dirección y curvas de solución para las ecuaciones diferenciales:

• \(y'=\frac{x^2-y^2}{1+x^2+y^2}\),
• \(y'=1+xy^2\), y
• \(y'=\frac{x-y}{1+x^2}\).

que son todos de la forma Ecuación\ ref {eq:1.3.1} con\(f\) continuo para todos\((x,y)\).

Figura 1.3.2 : Una dirección y curvas integrales para\(y'= {\frac{x^2-y^2}{1+x^2+y^2}}\).

Figura 1.3.3 : Una dirección y curvas integrales para\(y'= 1 + xy^2\).

Figura 1.3.4 : Una dirección y curvas integrales para\(y'= {\frac{x-y}{1+x^2}}\).

Los métodos del Capítulo 3 no funcionarán para la ecuación\[\label{eq:1.3.2} y'=-x/y\]

si\(R\) contiene parte del\(x\) eje -, ya que no\(f(x,y)=-x/y\) está definido cuando\(y=0\). Del mismo modo, no funcionarán para la ecuación

\[\label{eq:1.3.3} y'={x^2\over1-x^2-y^2}\]

if\(R\) contiene alguna parte del círculo unitario\(x^2+y^2=1\), porque el lado derecho de la ecuación\ ref {eq:1.3.3} no está definido si\(x^2+y^2=1\). Sin embargo, la ecuación\ ref {eq:1.3.2} y la ecuación\ ref {eq:1.3.3} pueden escribirse como

\[\label{eq:1.3.4} y'={A(x,y)\over B(x,y)}\]

donde\(A\) y\(B\) son continuas en cualquier rectángulo\(R\). Debido a esto, algún software de ecuaciones diferenciales se basa en resolver numéricamente pares de ecuaciones de la forma

\[\label{eq:1.3.5} {dx\over dt}=B(x,y),\quad {dy\over dt}=A(x,y)\]

donde\(x\) y\(y\) se consideran como funciones de un parámetro\(t\). Si\(x=x(t)\) y\(y=y(t)\) satisfacer estas ecuaciones, entonces

\[y'={dy\over dx}={dy\over dt}\left/{dx\over dt}\right.={A(x,y)\over B(x,y)},\nonumber\]

así\(y=y(x)\) satisface la Ecuación\ ref {eq:1.3.4}.

Las ecuaciones\ ref {eq:1.3.2} y\ ref {eq:1.3.3} se pueden reformular como en la Ecuación\ ref {eq:1.3.4} con\[{dx\over dt}=-y,\quad {dy\over dt}=x\nonumber\]

y

\[{dx\over dt}=1-x^2-y^2,\quad {dy\over dt}=x^2,\nonumber \]

respectivamente. Incluso si\(f\) es continuo y por lo demás “agradable” en todo momento\(R\), su software puede requerir que reformule la ecuación\(y'=f(x,y)\) como

\[{dx\over dt}=1,\quad {dy\over dt}=f(x,y),\nonumber \]

que es de la forma Ecuación\ ref {eq:1.3.5} con\(A(x,y)=f(x,y)\) y\(B(x,y)=1\).

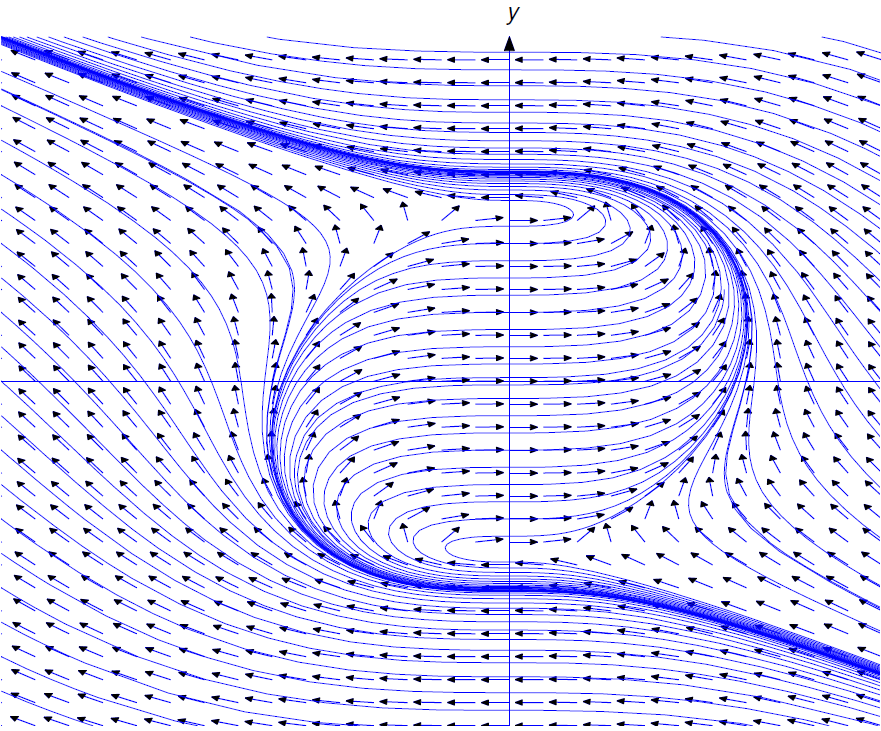
La Figura 1.3.5 muestra un campo de dirección y algunas curvas integrales para la Ecuación\ ref {eq:1.3.2}. Como vimos en Ejemplo [ejemplo:1.2.1} y volveremos a verificar en la Sección 2.2, las curvas integrales de la Ecuación\ ref {eq:1.3.2} son círculos centrados en el origen.

Figura 1.3.5 : Un campo de dirección y curvas integrales para\(y'=- {x\over y}\)

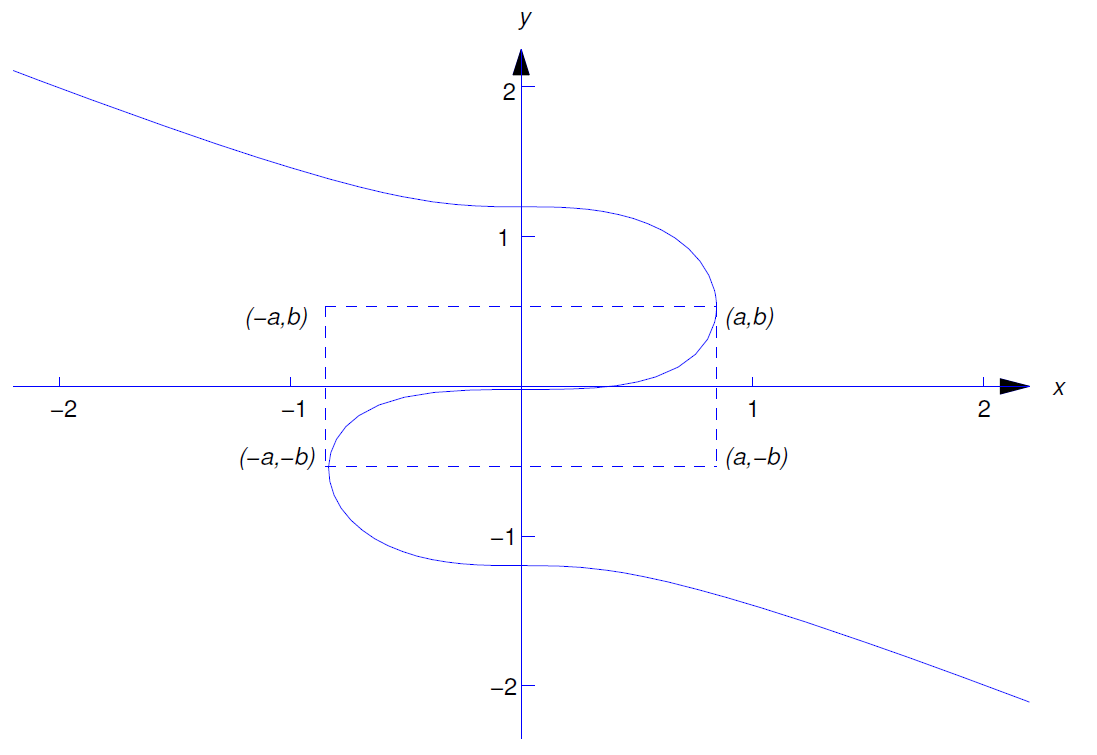
La figura 1.3.6 muestra un campo de dirección y algunas curvas integrales para la ecuación\ ref {eq:1.3.3}. Las curvas integrales cerca de la parte superior e inferior son curvas de solución. Sin embargo, las curvas integrales cercanas a la mitad son más complicadas. Por ejemplo, la Figura 1.3.7 muestra la curva integral a través del origen. Los vértices del rectángulo discontinuo están en el círculo\(x^2+y^2=1\) (\(a\approx.846\),\(b\approx.533\)), donde todas las curvas integrales de la Ecuación\ ref {eq:1.3.3} tienen pendiente infinita. Hay tres curvas de solución de la Ecuación\ ref {eq:1.3.3} en la curva integral de la figura: el segmento por encima del nivel\(y=b\) es la gráfica de una solución en\((-\infty,a)\), el segmento por debajo del nivel\(y=-b\) es la gráfica de una solución en\((-a,\infty)\), y el segmento entre estos dos niveles es el gráfico de una solución en\((-a,a)\).

Figura 1.3.6 : Un campo de dirección y curvas integrales para\(y'= \dfrac{x^2}{1-x^2-y^2}\).

Figura 1.3.7 : Un campo de dirección y curvas integrales para\(y'=- {x\over y}\)

Uso de la tecnología

Al estudiar a partir de este libro, a menudo se le pedirá que use software de computadora y gráficos. Los ejercicios con esta intención se marcan como (se requiere computadora o calculadora), (se requiere computadora y/o gráficos) o (trabajos de laboratorio que requieren software y/o gráficos). A menudo es posible que no entiendas completamente cómo el software hace lo que hace. Esto es similar a la situación en la que se encuentra la mayoría de las personas cuando conducen automóviles o ven televisión, y no disminuye el valor de usar la tecnología moderna como ayuda para el aprendizaje. Solo ten cuidado de que uses la tecnología como un suplemento al pensamiento en lugar de un sustituto de ella.