1.3E: Campos de dirección para ecuaciones de primer orden (ejercicios)

Última actualización
Guardar como PDF

Page ID: 114594

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Ejercicios para la Sección 1.3

En los Ejercicios 1—11 se dibuja un campo de dirección para la ecuación dada. Dibuja algunas curvas integrales.

1.
$clipboard_ecaa0db6f1fdef51a705e90b878c02022.png$
Figura 1.3E.1 : Un campo de dirección para$y'= {\frac{x}{y}}$

2.
$clipboard_e36fdf613776a431b1e8191cecfb75d19.png$
Figura 1.3E.2 : Un campo de dirección para$ {y'= {2xy^2\over1+x^2}}$

3.
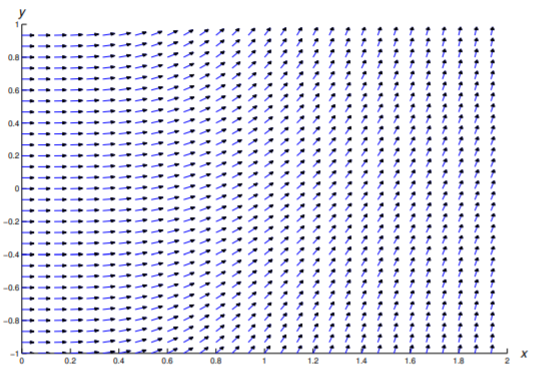
$clipboard_e2e0f78fd7d0281deeb3df372a3dd82bf.png$
Figura 1.3E.3 : Un campo de dirección para$y'=x^2(1+y^2)$

4.
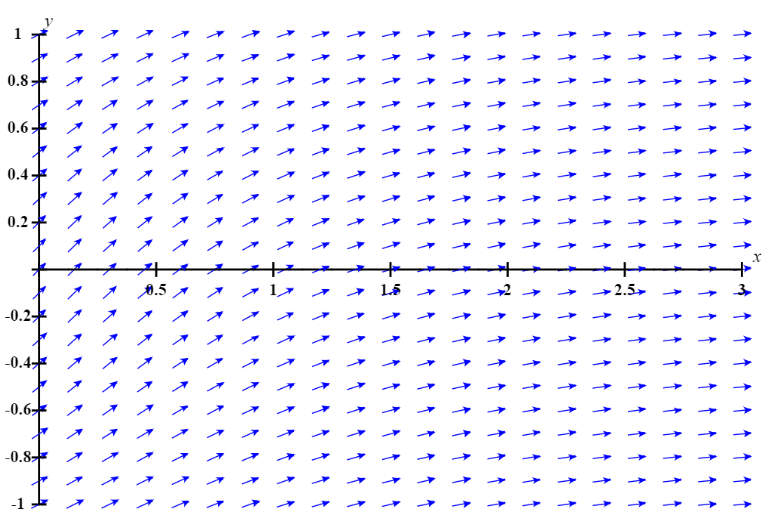
$clipboard_eaeb583fc57656cdd45141b50283234ba.png$
Figura 1.3E.4 : Un campo de dirección para$y'= {1\over1+x^2+y^2}$

5.

$clipboard_e773af5b2db36a2716990bc6547ea8350.png$
Figura 1.3E.5 : Un campo de dirección para$y'=-(2xy^2+y^3)$

6.
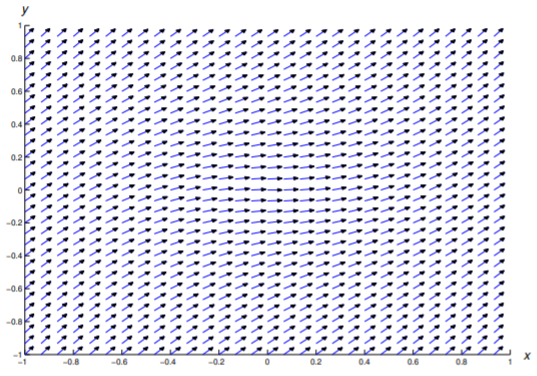
$clipboard_e608ddd48ea3de96fabef8c8dbc9f2b95.png$
Figura 1.3E.6 : Un campo de dirección para$y'=(x^2+y^2)^{1/2}$

7.
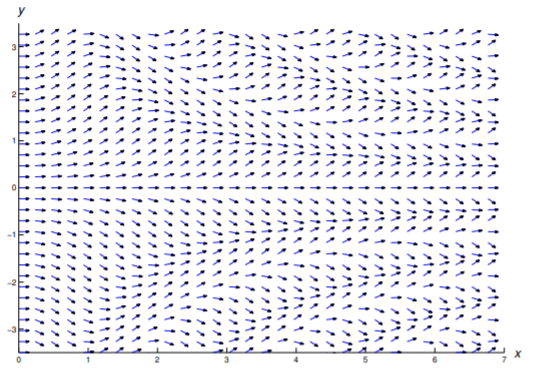
$clipboard_e4c24dceacf5c04358243ff0dbcfab51f.png$
Figura 1.3E.7 : Un campo de dirección para$y'=\sin xy$

8.
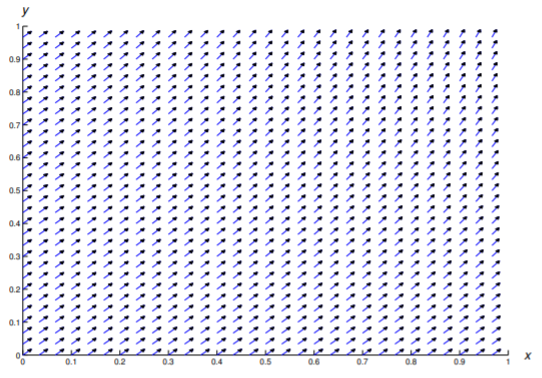
$clipboard_ea448bb2833068eee5327e80c03f3bc30.png$
Figura 1.3E.8 : Un campo de dirección para$y'=e^{xy}$

9.
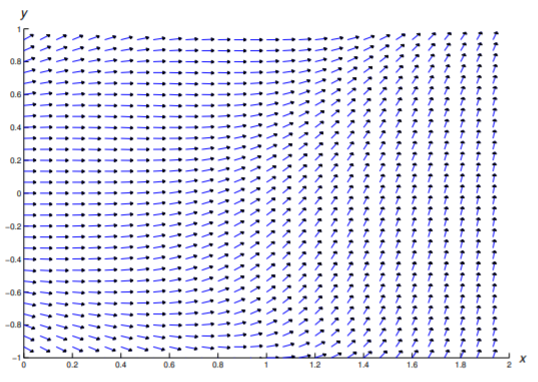
$clipboard_e994c3c42adb6dd58d08b10ccb5b0549c.png$
Figura 1.3E.9 : Un campo de dirección para$y'=(x-y^2)(x^2-y)$

10.
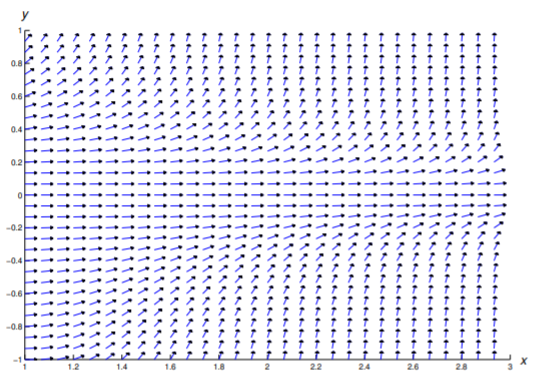
$clipboard_e06d564a692a46e7905532a83d418f113.png$
Figura 1.3E.10 : Un campo de dirección para$y'=x^3y^2+xy^3$

11.
$clipboard_e1a0943243a0e768584defadf1c51a9d4.png$
Figura 1.3E.11 : Un campo de dirección para$y'=\sin(x-2y)$

En los Ejercicios 12 - 22 construir un campo de dirección y trazar algunas curvas integrales en la región rectangular indicada.

12. $y'=y(y-1); \quad \{-1\le x\le 2,\ -2\le y\le2\}$

13. $y'=2-3xy; \quad \{-1\le x\le 4,\ -4\le y\le4\}$

14. $y'=xy(y-1); \quad \{-2\le x\le2,\ -4\le y\le 4\}$

15. $y'=3x+y; \quad \{-2\le x\le2,\ 0\le y\le 4\}$

16. $y'=y-x^3; \quad \{-2\le x\le2,\ -2\le y\le 2\}$

17. $y'=1-x^2-y^2; \quad \{-2\le x\le2,\ -2\le y\le 2\}$

18. $y'=x(y^2-1); \quad \{-3\le x\le3,\ -3\le y\le 2\}$

19. $y'= {x\over y(y^2-1)}; \quad \{-2\le x\le2,\ -2\le y\le 2\}$

20. $y'= {xy^2\over y-1}; \quad \{-2\le x\le2,\ -1\le y\le 4\}$

21. $y'= {x(y^2-1)\over y}; \quad \{-1\le x\le1,\ -2\le y\le 2\}$

22. $y'=- {x^2+y^2\over1-x^2-y^2}; \quad \{-2\le x\le2,\ -2\le y\le 2\}$

23. Renombrando adecuadamente las constantes y variables dependientes en las ecuaciones

\[T' = -k(T-T_m) \tag{A}\]

\[G'=-\lambda G+r\tag{B}\]

discutido en la Sección 1.2 en relación con la ley de Newton de enfriamiento y absorción de glucosa en el cuerpo, podemos escribir ambos como

\[y'=- ay+b, \tag{C}\]

donde$a$ es una constante positiva y$b$ es una constante arbitraria. Así, (A) es de la forma (C) con$y=T$,$a=k$, y$b=kT_m$, y (B) es de la forma (C) con$y=G$,$a=\lambda$, y$b=r$. Encontraremos ecuaciones de la forma (C) en muchas otras aplicaciones en el Capítulo 2.

Elige un positivo$a$ y uno arbitrario$b$. Construir un campo de dirección y trazar algunas curvas integrales para (C) en una región rectangular de la forma\[\{0\le t\le T,\ c\le y\le d\}\]

del$ty$ -avión. $T$Varía$c$,, y$d$ hasta que descubras una propiedad común de todas las soluciones de (C). Repita este experimento con varias opciones de$a$ y$b$ hasta que pueda declarar esta propiedad precisamente en términos de$a$ y$b$.

24. Renombrando adecuadamente las constantes y variables dependientes en las ecuaciones

\[P'=aP(1-\alpha P) \tag{A}\]

\[I'=rI(S-I) \tag{B}\]

discutido en la Sección 1.1 en relación con el modelo poblacional de Verhulst y la propagación de una epidemia, podemos escribir ambos en la forma

\[y'=ay-by^2, \tag{C}\]

donde$a$ y$b$ son constantes positivas. Así, (A) es de la forma (C) con$y=P$,$a=a$, y$b=a\alpha$, y (B) es de la forma (C) con$y=I$,$a=rS$, y$b=r$. En el Capítulo 2 encontraremos ecuaciones de la forma (C) en otras aplicaciones.

Elija números positivos$a$ y$b$. Construir un campo de dirección y trazar algunas curvas integrales para (C) en una región rectangular de la forma\[\{0\le t\le T,\ 0\le y\le d\}\]

del$ty$ -avión. $T$Varía y$d$ hasta que descubras una propiedad común de todas las soluciones de (C) con$y(0)>0$. Repita este experimento con varias opciones de$a$ y$b$ hasta que pueda declarar esta propiedad precisamente en términos de$a$ y$b$.

Elija números positivos$a$ y$b$. Construir un campo de dirección y trazar algunas curvas integrales para (C) en una región rectangular de la forma\[\{0\le t\le T,\ c\le y\le 0\}\]

del$ty$ -avión. $a$Varía$b$,,$T$ y$c$ hasta que descubras una propiedad común de todas las soluciones de (C) con$y(0)<0$.

Puedes verificar tus resultados más adelante haciendo el Ejercicio 2.2.27.