2.3: Existencia y singularidad de soluciones de ecuaciones no lineales
- Page ID
- 115151
Si bien existen métodos para resolver algunas ecuaciones no lineales, es imposible encontrar fórmulas útiles para las soluciones de la mayoría. Ya sea que estemos buscando soluciones exactas o aproximaciones numéricas, es útil conocer condiciones que implican la existencia y singularidad de soluciones de problemas de valor inicial para ecuaciones no lineales. En esta sección señalamos tal condición y la ilustramos con ejemplos.
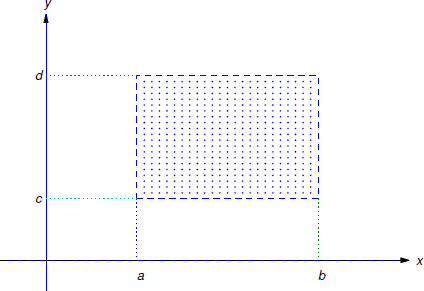
Alguna terminología: un rectángulo abierto\(R\) es un conjunto de puntos\((x,y)\) tal que
\[a<x<b\quad\text{and}\quad c<y<d\nonumber \]
(Figura 2.3.1 ). Vamos a denotar este conjunto por\(R: \{ a < x < b, c < y < d \}\). “Abierto” significa que el rectángulo límite (indicado por las líneas discontinuas en la Figura 2.3.1 ) no está incluido en\(R\).
El siguiente teorema da condiciones suficientes para la existencia y singularidad de soluciones de problemas de valor inicial para ecuaciones diferenciales no lineales de primer orden. Omitimos la prueba, que está más allá del alcance de este libro.
- Si\(f\) es continuo en un rectángulo abierto\[R: \{ a < x < b, c < y < d \} \nonumber\] que contiene\((x_0,y_0)\) entonces el problema del valor inicial\[\label{eq:2.3.1} y'=f(x,y), \quad y(x_0)=y_0\] tiene al menos una solución en algún subintervalo abierto de\((a,b)\) que contiene\(x_0.\)
- Si ambos\(f\) y\(f_y\) son continuos\(R\) entonces la Ecuación\ ref {eq:2.3.1} tiene una solución única en algún subintervalo abierto de\((a,b)\) que contiene\(x_0\)
Es importante entender exactamente lo que dice el Teorema 2.3.1 .
- (a) es un teorema de existencia. Garantiza que existe una solución en algún intervalo abierto que contiene\(x_0\), pero no proporciona información sobre cómo encontrar la solución, o para determinar el intervalo abierto en el que existe. Además, (a) no proporciona información sobre el número de soluciones que la Ecuación\ ref {eq:2.3.1} puede tener. Deja abierta la posibilidad de que la Ecuación\ ref {eq:2.3.1} pueda tener dos o más soluciones que difieran para valores de\(x\) arbitrariamente cercanos a\(x_0\). Veremos en Ejemplo 2.3.6 que esto puede suceder.
- (b) es un teorema de singularidad. Garantiza que la Ecuación\ ref {eq:2.3.1} tiene una solución única en algún intervalo abierto (a, b) que contiene\(x_0\). Sin embargo, si\((a,b)\ne(-\infty,\infty)\), Ecuación\ ref {eq:2.3.1} puede tener más de una solución en un intervalo mayor que contenga\((a,b)\). Por ejemplo, puede suceder que\(b<\infty\) y todas las soluciones tengan los mismos valores en\((a,b)\), pero dos soluciones\(y_1\) y\(y_2\) se definan en algún intervalo\((a,b_1)\) con\(b_1>b\), y tienen valores diferentes para\(b<x<b_{1}\); así, las gráficas de la rama\(y_1\) y\(y_2\) “ off” en diferentes direcciones en\(x = b\). (Consulte Ejemplo 2.3.7 y Figura 2.3.3 ). En este caso, la continuidad implica eso\(y_{1}(b) = y_{2}(b)\) (llamar a su valor común\(y\)),\(y_{1}\) y y ambas\(y_{2}\) son soluciones del problema de valor inicial
\[\label{eq:2.3.2}y=f(x,y),\quad y(b)=\overline{y}\]
que difieren en cada intervalo abierto que contiene\(b\). Por lo tanto\(f\) o\(f_y\) debe tener una discontinuidad en algún punto en cada rectángulo abierto que contenga\((b, y)\), ya que si esto no fuera así,\ ref {eq:2.3.2} tendría una solución única en algún intervalo abierto que contenga\(b\). Te dejamos a ti dar un análisis similar del caso donde\(a > −∞\).
Considerar el problema de valor inicial
\[\label{eq:2.3.3} y'={x^2-y^2 \over 1+x^2+y^2}, \quad y(x_0)=y_0.\]
Desde
\[f(x,y) = {x^2-y^2 \over 1+x^2+y^2} \quad \text{and} \quad f_y(x,y) = -{2y(1+2x^2)\over (1+x^2+y^2)^2} \nonumber\]
son continuos para todos\((x,y)\), el Teorema 2.3.1 implica que si\((x_0,y_0)\) es arbitrario, entonces la Ecuación\ ref {eq:2.3.3} tiene una solución única en algún intervalo abierto que contiene\(x_0\).
Considerar el problema de valor inicial
\[\label{eq:2.3.4} y'={x^2-y^2 \over x^2+y^2}, \quad y(x_0)=y_0.\]
Aquí
\[f(x,y) = {x^2-y^2 \over x^2+y^2}\quad \text{and} \quad f_y(x,y) = -{4x^2y \over (x^2+y^2)^2} \nonumber\]
son continuos en todas partes excepto en\((0,0)\). Si\((x_0,y_0) \ne(0,0)\), hay un rectángulo abierto\(R\) que contiene\((x_0,y_0)\) que no contiene\((0,0)\). Dado que\(f\) y\(f_y\) son continuos en\(R\), Teorema 2.3.1 implica que si\((x_0,y_0)\ne(0,0)\) entonces Ecuación\ ref {eq:2.3.4} tiene una solución única en algún intervalo abierto que contiene\(x_0\).
Considerar el problema de valor inicial
\[\label{eq:2.3.5} y'={x+y\over x-y},\quad y(x_0)=y_0.\]
Aquí
\[f(x,y) = {x+y\over x-y}\quad \text{and} \quad f_y(x,y) = {2x\over (x-y)^2} \nonumber\]
son continuos en todas partes excepto en la línea\(y=x\). Si\(y_0\ne x_0\), hay un rectángulo abierto\(R\) que contiene\((x_0,y_0)\) que no intersecta la línea\(y=x\). Dado que\(f\) y\(f_y\) son continuos en\(R\), Teorema 2.3.1 implica que si\(y_0\ne x_0\), Ecuación\ ref {eq:2.3.5} tiene una solución única en algún intervalo abierto que contiene\(x_0\).
En el Ejemplo 2.2.4, vimos que las soluciones de
\[\label{eq:2.3.6} y'=2xy^2\]
son
\[y\equiv0\quad \text{and} \quad y=-{1 \over x^2+c}, \nonumber\]
donde\(c\) es una constante arbitraria. En particular, esto implica que ninguna solución de la Ecuación\ ref {eq:2.3.6} que no\(y\equiv0\) pueda ser igual a cero para cualquier valor de\(x\). Demostrar que el Teorema\(\PageIndex{1b}\) implica esto.
Obtendremos una contradicción asumiendo que la Ecuación\ ref {eq:2.3.6} tiene una solución\(y_1\) que es igual a cero para algún valor de\(x\), pero no es idéntico a cero. Si\(y_1\) tiene esta propiedad, hay un punto\(x_0\) tal que\(y_1(x_0)=0\), pero\(y_1(x)\ne0\) por algún valor de\(x\) en cada intervalo abierto que contiene\(x_0\). Esto significa que el problema del valor inicial
\[\label{eq:2.3.7} y'=2xy^2,\quad y(x_0)=0\]
tiene dos soluciones\(y\equiv0\) y\(y=y_1\) que difieren por algún valor de\(x\) en cada intervalo abierto que contiene\(x_0\). Esto contradice el Teorema 2.3.1 (b), ya que en la Ecuación\ ref {eq:2.3.6} las funciones
\[f(x,y)=2xy^2 \quad \text{and} \quad f_y(x,y)= 4xy. \nonumber\]
son ambos continuos para todos\((x,y)\), lo que implica que la Ecuación\ ref {eq:2.3.7} tiene una solución única en algún intervalo abierto que contiene\(x_0\).
Considerar el problema de valor inicial
\[\label{eq:2.3.8} y' = {10\over 3}xy^{2/5}, \quad y(x_0) = y_0.\]
- ¿Para qué puntos\((x_0,y_0)\)\(\PageIndex{1a}\) implica el Teorema que la Ecuación\ ref {eq:2.3.8} tiene una solución?
- ¿Para qué puntos\((x_0,y_0)\)\(\PageIndex{1b}\) implica el Teorema que la Ecuación\ ref {eq:2.3.8} tiene una solución única en algún intervalo abierto que contiene\(x_0\)?
Solución a
Desde
\[f(x,y) = {10\over 3}xy^{2/5} \nonumber\]
es continuo para todos\((x,y)\), el teorema 2.3.1 implica que la Ecuación\ ref {eq:2.3.8} tiene una solución para cada\((x_0,y_0)\).
Solución b
Aquí
\[f_y(x,y) = {4 \over 3}xy^{-3/5} \nonumber\]
es continuo para todos\((x,y)\) con\(y\ne 0\). Por lo tanto, si\(y_0\ne0\) hay un rectángulo abierto en el que ambos\(f\) y\(f_y\) son continuos, y el Teorema 2.3.1 implica que la Ecuación\ ref {eq:2.3.8} tiene una solución única en algún intervalo abierto que contiene\(x_0\).
Si\(y=0\) entonces\(f_y(x,y)\) es indefinido, y por lo tanto discontinuo; por lo tanto, el Teorema 2.3.1 no se aplica a la Ecuación\ ref {eq:2.3.8} if\(y_0=0\).
Ejemplo 2.3.5 deja abierta la posibilidad de que el problema de valor inicial
\[\label{eq:2.3.9} y'={10 \over 3}xy^{2/5}, \quad y(0)=0\]
tiene más de una solución en cada intervalo abierto que contiene\(x_0=0\). Demuestre que esto es cierto.
Solución
Por inspección,\(y\equiv0\) es una solución de la ecuación diferencial
\[\label{eq:2.3.10} y'={10 \over 3} xy ^{2/5}.\]
Dado que\(y\equiv0\) satisface la condición inicial\(y(0)=0\), es una solución de Ecuación\ ref {eq:2.3.9}.
Ahora supongamos que\(y\) es una solución de Ecuación\ ref {eq:2.3.10} que no es idénticamente cero. Separar variables en Ecuación\ ref {eq:2.3.10} rendimientos
\[y^{-2/5}y'={10 \over 3}x \nonumber\]
en cualquier intervalo abierto donde no\(y\) tenga ceros. Integrando esto y reescribiendo la constante arbitraria como\(5c/3\) rendimientos
\[{5\over 3}y^{3/5} = {5\over 3}(x^2+c) . \nonumber\]
Por lo tanto
\[\label{eq:2.3.11} y = (x^2+c)^{5/3}. \]
Ya que dividimos por\(y\) para separar variables en la Ecuación\ ref {eq:2.3.10}, nuestra derivación de la Ecuación\ ref {eq:2.3.11} es legítima solo en intervalos abiertos donde no\(y\) tiene ceros. Sin embargo, la Ecuación\ ref {eq:2.3.11} define realmente\(y\) para todos\(x\), y la ecuación diferenciadora\ ref {eq:2.3.11} muestra que
\[\begin{aligned}y'={10 \over 3}x(x^2+c)^{2/3}={10 \over 3}xy^{2/5},\,-\infty < x < \infty\end{aligned} \]
Por lo tanto, la ecuación\ ref {eq:2.3.11} satisface la ecuación\ ref {eq:2.3.10} en\((-\infty,\infty)\) incluso si\(c\le 0\), para que\(y(\sqrt{|c|})=y(-\sqrt{|c|})=0\). En particular, tomando\(c=0\) en la ecuación\ ref {eq:2.3.11} rendimientos
\[y=x^{10/3} \nonumber\]
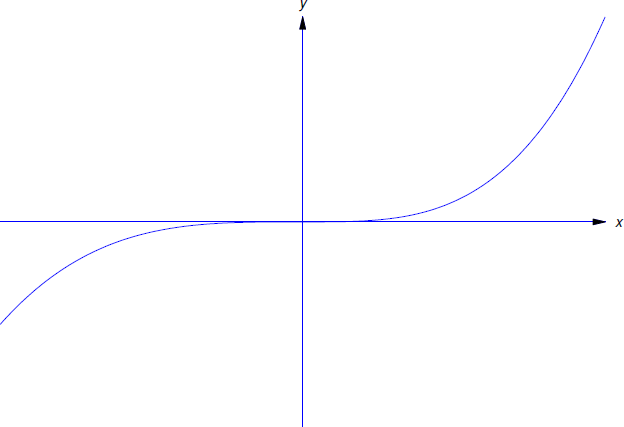
como una segunda solución de la Ecuación\ ref {eq:2.3.9}. Ambas soluciones se definen en\((-\infty,\infty)\), y difieren en cada intervalo abierto que contiene\(x_0=0\) (Figura 2.3.2 ). De hecho, hay cuatro soluciones distintas de Ecuación\ ref {eq:2.3.9} definidas en\((-\infty,\infty)\) que difieren entre sí en cada intervalo abierto que contiene\(x_0=0\). ¿Se pueden identificar los otros dos?
Del ejemplo 2.3.5 , el problema del valor inicial
\[\label{eq:2.3.12} y'={10 \over 3}xy^{2/5}, \quad y(0)=-1\]
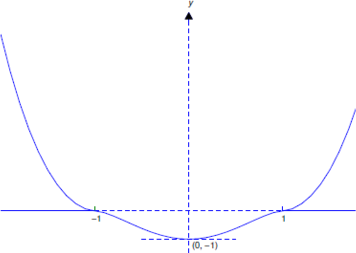
tiene una solución única en algún intervalo abierto que contiene\(x_0=0\). Encuentre una solución y determine el intervalo abierto más grande\((a,b)\) en el que es único.
Solución
\(y\)Sea cualquier solución de Ecuación\ ref {eq:2.3.12}. Debido a la condición inicial\(y(0)=-1\) y la continuidad de\(y\), hay un intervalo abierto\(I\) que contiene\(x_0=0\) sobre el que no\(y\) tiene ceros, y en consecuencia es de la forma Ecuación\ ref {eq:2.3.11}. Ajuste\(x=0\) y\(y=-1\) en Ecuación\ ref {eq:2.3.11} rendimientos\(c=-1\), entonces
\[\label{eq:2.3.13} y=(x^2-1)^{5/3}\]
para\(x\) en\(I\). Por lo tanto, cada solución de la Ecuación\ ref {eq:2.3.12} difiere de cero y viene dada por la Ecuación\ ref {eq:2.3.13} on\((-1,1)\); es decir, la Ecuación\ ref {eq:2.3.13} es la solución única de la Ecuación\ ref {eq:2.3.12} on\((-1,1)\). Este es el intervalo abierto más grande en el que la Ecuación\ ref {eq:2.3.12} tiene una solución única. Para ver esto, tenga en cuenta que la Ecuación\ ref {eq:2.3.13} es una solución de la Ecuación\ ref {eq:2.3.12} on\((-\infty,\infty)\). Del Ejercicio 2.2.15, hay infinitamente muchas otras soluciones de la Ecuación\ ref {eq:2.3.12} que difieren de la Ecuación\ ref {eq:2.3.13} en cada intervalo abierto mayor que\((-1,1)\). Una de esas soluciones es
\[y = \left\{ \begin{array}{cl} (x^2-1)^{5/3}, & -1 \le x \le 1, \\[6pt] 0, & |x|>1. \end{array} \right. \nonumber\]
Del ejemplo 2.3.5 ), el problema del valor inicial
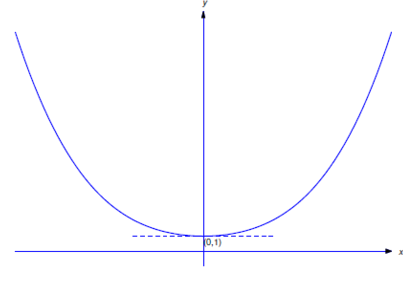
\[\label{eq:2.3.14} y'={10 \over 3}xy^{2/5}, \quad y(0)=1\]
tiene una solución única en algún intervalo abierto que contiene\(x_0=0\). Encuentre la solución y determine el intervalo abierto más grande en el que es único.
Solución
\(y\)Sea cualquier solución de Ecuación\ ref {eq:2.3.14}. Debido a la condición inicial\(y(0)=1\) y la continuidad de\(y\), hay un intervalo abierto\(I\) que contiene\(x_0=0\) sobre el que no\(y\) tiene ceros, y en consecuencia es de la forma Ecuación\ ref {eq:2.3.11}. Ajuste\(x=0\) y\(y=1\) en Ecuación\ ref {eq:2.3.11} rendimientos\(c=1\), entonces
\[\label{eq:2.3.15} y=(x^2+1)^{5/3}\]
para\(x\) en\(I\). Por lo tanto, cada solución de la Ecuación\ ref {eq:2.3.14} difiere de cero y viene dada por la Ecuación\ ref {eq:2.3.15} on\((-\infty,\infty)\); es decir, la Ecuación\ ref {eq:2.3.15} es la solución única de la Ecuación\ ref {eq:2.3.14} on\((-\infty,\infty)\). La figura 2.3.4 ) muestra la gráfica de esta solución.