2.4: Transformación de ecuaciones no lineales en ecuaciones separables
- Page ID
- 115150
En la Sección 2.1, encontramos que las soluciones de una ecuación lineal no homogénea
\[y'+p(x)y=f(x)\nonumber \]
son de la forma\(y=uy_1\), donde\(y_1\) es una solución no trivial de la ecuación complementaria
\[\label{eq:2.4.1} y'+p(x)y=0\]
y\(u\) es una solución de
\[u'y_1(x)=f(x).\nonumber \]
Tenga en cuenta que esta última ecuación es separable, ya que puede reescribirse como
\[u'={f(x)\over y_1(x)}.\nonumber \]
En esta sección consideraremos ecuaciones diferenciales no lineales que no son separables para empezar, sino que pueden resolverse de manera similar escribiendo sus soluciones en la forma\(y=uy_1\), donde\(y_1\) es una función conocida adecuadamente elegida y\(u\) satisface una ecuación separable. Digamos en este caso que transformamos la ecuación dada en una ecuación separable.
Ecuaciones de Bernoulli
Una ecuación de Bernoulli es una ecuación de la forma
\[\label{eq:2.4.2} y'+p(x)y=f(x)y^r,\]
donde\(r\) puede haber cualquier número real que no sea\(0\) o\(1\). (Tenga en cuenta que la ecuación\ ref {eq:2.4.2} es lineal si y solo si\(r=0\) o\(r=1\).) Podemos transformar la Ecuación\ ref {eq:2.4.2} en una ecuación separable por variación de parámetros: si\(y_1\) es una solución no trivial de la Ecuación\ ref {eq:2.4.1}, sustituyendo\(y=uy_1\) en Ecuación\ ref {eq:2.4.2} rendimientos
\[u'y_1+u(y_1'+p(x)y_1)=f(x)(uy_1)^r,\nonumber \]
que es equivalente a la ecuación separable
\[u'y_1(x)=f(x)\left(y_1(x)\right)^ru^r \quad \text{or} \quad {u'\over u^r}=f(x)\left(y_1(x)\right)^{r-1},\nonumber \]
ya que\(y_1'+p(x)y_1=0\).
Resuelve la ecuación de Bernoulli
\[\label{eq:2.4.3} y'-y=xy^2.\]
Ya que\(y_1=e^x\) es una solución de\(y'-y=0\), buscamos soluciones de Ecuación\ ref {eq:2.4.3} en la forma\(y=ue^x\), donde
\[u'e^x=xu^2e^{2x} \quad \text{or equivalently} \quad u'=xu^2e^x. \nonumber\]
Separación de rendimientos de variables
\[{u'\over u^2}=xe^x, \nonumber\]
e integrando rendimientos
\[-{1\over u}=(x-1)e^x+c. \nonumber\]
Por lo tanto,
\[u=-{1\over(x-1)e^x+c} \nonumber\]
y
\[y=-{1\over x-1+ce^{-x}}. \nonumber\]
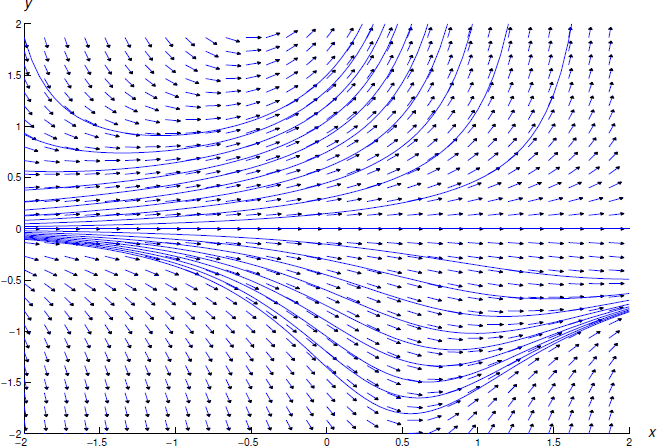
La figura 2.4.1 muestra el campo de dirección y algunas curvas integrales de la ecuación\ ref {eq:2.4.3}.
Otras ecuaciones no lineales que pueden transformarse en ecuaciones separables
Hemos visto que la ecuación no lineal de Bernoulli se puede transformar en una ecuación separable por la sustitución\(y=uy_1\) si\(y_1\) se elige adecuadamente. Ahora descubramos una condición suficiente para una ecuación diferencial de primer orden no lineal
\[\label{eq:2.4.4} y'=f(x,y)\]
para ser transformable en una ecuación separable de la misma manera. Sustituyendo\(y=uy_1\) en Ecuación\ ref {eq:2.4.4} rendimientos
\[u'y_1(x)+uy_1'(x)=f(x,uy_1(x)),\nonumber \]
que es equivalente a
\[\label{eq:2.4.5} u'y_1(x)=f(x,uy_1(x))-uy_1'(x).\]
Si
\[f(x,uy_1(x))=q(u)y_1'(x)\nonumber \]
para alguna función\(q\), entonces la Ecuación\ ref {eq:2.4.5} se convierte
\[\label{eq:2.4.6} u'y_1(x)=(q(u)-u)y_1'(x),\]
que es separable. Después de verificar soluciones constantes de\(u\equiv u_0\) tal manera que\(q(u_0)=u_0\), podemos separar variables para obtener
\[{u'\over q(u)-u}={y_1'(x)\over y_1(x)}. \nonumber\]
Ecuaciones homogéneas no lineales
En el texto consideraremos únicamente la clase de ecuaciones más estudiada para la que funciona el método del párrafo anterior. Otros tipos de ecuaciones aparecen en Ejercicios 2.4.44 - 2.4.51 .
Se dice que la ecuación diferencial Ecuación\ ref {eq:2.4.4} es homogénea si\(x\) y\(y\) ocurre de tal\(f\) manera que\(f(x,y)\) depende solo de la relación\(y/x\); es decir, la ecuación\ ref {eq:2.4.4} puede escribirse como
\[\label{eq:2.4.7} y'=q(y/x),\]
donde\(q=q(u)\) es una función de una sola variable. Por ejemplo,
\[y'={y+xe^{-y/x}\over x}={y\over x}+e^{-y/x}\nonumber \]
y
\[y'={y^2+xy-x^2\over x^2}=\left(y\over x\right)^2+{y\over x} -1\nonumber \]
son de la forma Ecuación\ ref {eq:2.4.7}, con
\[q(u)=u+e^{-u} \quad \text{and} \quad q(u)=u^2+u-1,\nonumber \]
respectivamente. El método general discutido anteriormente se puede aplicar a la Ecuación\ ref {eq:2.4.7} con\(y_1=x\) (y por lo tanto\(y_1'=1)\). Así, sustituyendo\(y=ux\) en la Ecuación\ ref {eq:2.4.7} rinde
\[u'x+u=q(u),\nonumber \]
y separación de variables (después de verificar soluciones constantes\(u\equiv u_0\) tales que\(q(u_0)=u_0\)) rinde
\[{u'\over q(u)-u}={1\over x}.\nonumber \]
Antes de pasar a los ejemplos, señalamos algo que quizás ya hayas notado: la definición de ecuación homogénea dada aquí no es la misma que la definición dada en la Sección 2.1, donde dijimos que una ecuación lineal de la forma
\[y'+p(x)y=0\nonumber \]
es homogéneo. No nos disculpamos por esta inconsistencia, ya que no la creamos históricamente, homogéneo se ha utilizado en estas dos formas inconsistentes. El que tiene que ver con ecuaciones lineales es lo más importante. Esta es la única sección del libro donde se aplicará el significado aquí definido.
Ya que en general\(y/x\) es indefinido si\(x=0\), consideraremos soluciones de ecuaciones no homogéneas solo en intervalos abiertos que no contengan el punto\(x=0\).
Resolver
\[\label{eq:2.4.8} y'={y+xe^{-y/x}\over x}.\]
Sustituyendo\(y=ux\) en Ecuación\ ref {eq:2.4.8} rendimientos
\[u'x+u = {ux+xe^{-ux/x}\over x} = u+e^{-u}. \nonumber\]
Simplificación y separación de rendimientos de variables
\[e^uu'={1\over x}. \nonumber\]
Integración de rendimientos\(e^u=\ln |x|+c\). Por lo tanto\(u=\ln(\ln|x|+c)\) y\(y=ux=x \ln (\ln |x|+c)\).
La Figura 2.4.2 muestra un campo de dirección y curvas integrales para la Ecuación\ ref {eq:2.4.8}.

a. Resolver
\[\label{eq:2.4.9} x^2y'=y^2+xy-x^2.\]
b. Resolver el problema de valor inicial
\[\label{eq:2.4.10} x^2y'=y^2+xy-x^2, \quad y(1)=2.\]
Solución a
Primero encontramos soluciones de Ecuación\ ref {eq:2.4.9} en intervalos abiertos que no contienen\(x=0\). Podemos reescribir la ecuación\ ref {eq:2.4.9} como
\[y'={y^2+xy-x^2\over x^2} \nonumber\]
para\(x\) en cualquier intervalo de este tipo. Sustitución de\(y=ux\) rendimientos
\[u'x+u ={ (ux)^2+x(ux)-x^2 \over x^2} = u^2+u-1,\nonumber\]
por lo
\[\label{eq:2.4.11} u'x=u^2-1.\]
Por inspección esta ecuación tiene las soluciones constantes\(u\equiv1\) y\(u\equiv-1\). Por lo tanto\(y=x\) y\(y=-x\) son soluciones de Ecuación\ ref {eq:2.4.9}. Si\(u\) es una solución de Ecuación\ ref {eq:2.4.11} que no asume los valores\(\pm 1\) en algún intervalo, separar variables rinde
\[{u'\over u^2-1}={1\over x},\nonumber\]
o, después de una expansión parcial de la fracción,
\[{1\over 2}\left[{1\over u-1}-{1\over u+1}\right]u'= {1\over x}.\nonumber\]
Multiplicando por 2 e integrando rendimientos
\[\ln\left|u-1\over u+1\right| =2 \ln |x|+k,\nonumber\]
o
\[\left|{u-1\over u+1}\right|=e^kx^2,\nonumber\]
que se mantiene si
\[\label{eq:2.4.12} {u-1\over u+1}=cx^2 \]
donde\(c\) es una constante arbitraria. Resolviendo\(u\) rendimientos
\[u ={1+cx^2\over 1-cx^2}.\nonumber \]
Por lo tanto
\[\label{eq:2.4.13} y=ux={x(1+cx^2)\over 1-cx^2}\]
es una solución de la Ecuación\ ref {eq:2.4.10} para cualquier elección de la constante\(c\). El ajuste\(c=0\) en la ecuación\ ref {eq:2.4.13} produce la solución\(y=x\). Sin embargo, la solución no se\(y=-x\) puede obtener de la Ecuación\ ref {eq:2.4.13}. Así, las soluciones de la Ecuación\ ref {eq:2.4.9} en intervalos que no contienen\(x=0\) son\(y=-x\) y funciones de la forma Ecuación\ ref {eq:2.4.13}.
La situación es más complicada si\(x=0\) es el intervalo abierto. Primero, tenga en cuenta que\(y=-x\) satisface la Ecuación\ ref {eq:2.4.9} on\((-\infty,\infty)\). Si\(c_1\) y\(c_2\) son constantes arbitrarias, la función
\[\label{eq:2.4.14}y=\left\{\begin{array}{ll} {\frac{x(1+c_{1}x^{2})}{1-c_{1}x^{2}},}&{a<x<0} \\ {\frac{x(1+c_{2}x^{2}}{1-c_{2}x^{2}},}&{0\leq x<b}\end{array}\right.\]
es una solución de la Ecuación\ ref {eq:2.4.9} on\((a,b)\), donde
\[a=\left\{\begin{array}{cl}- {1\over\sqrt{c_1}}&\mbox{ if }c_1>0,\\ -\infty&\mbox{ if }c_1\le 0, \end{array}\right. \quad \text{and} \quad b=\left\{\begin{array}{cl} {1\over\sqrt{c_2}}&\mbox{ if }c_2>0,\\ \infty&\mbox{ if }c_2\le 0. \end{array}\right.\nonumber\]
Te dejamos a ti verificar esto. Para ello, tenga en cuenta que si\(y\) es alguna función de la forma Ecuación\ ref {eq:2.4.13} entonces\(y(0)=0\) y\(y'(0)=1\).
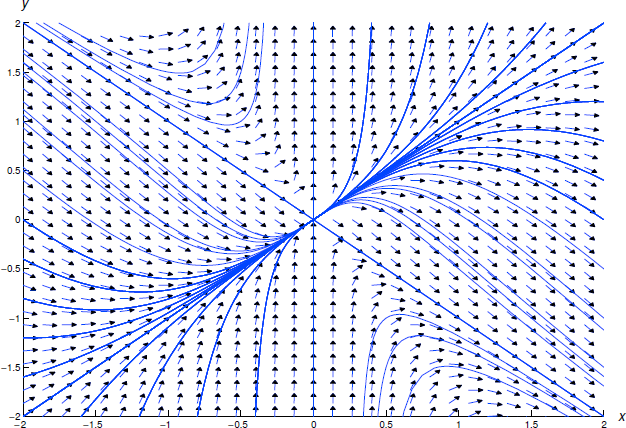
La Figura 2.4.3 muestra un campo de dirección y algunas curvas integrales para la Ecuación\ ref {eq:2.4.9}.
Solución b
Podríamos obtener\(c\) imponiendo la condición inicial\(y(1)=2\) en la Ecuación\ ref {eq:2.4.13}, y luego resolviendo para\(c\). Sin embargo, es más fácil usar la Ecuación\ ref {eq:2.4.12}. Ya que\(u=y/x\), la condición inicial\(y(1)=2\) implica que\(u(1)=2\). Sustituyendo esto en la Ecuación\ ref {eq:2.4.12} rinde\(c=1/3\). De ahí que la solución de la Ecuación\ ref {eq:2.4.10} es
\[y={x(1+x^2/3)\over 1-x^2/3}.\nonumber\]
El intervalo de validez de esta solución es\((-\sqrt3,\sqrt3)\). Sin embargo, el intervalo más grande en el que la Ecuación\ ref {eq:2.4.10} tiene una solución única es\((0,\sqrt3)\). Para ver esto, anote de la Ecuación\ ref {eq:2.4.14} que cualquier función de la forma
\[\label{eq:2.4.15} y=\left\{\begin{array}{ll} {\frac{x(1+cx^{2})}{1-cx^{2}},}&{a<x\leq 0} \\ {\frac{x(1+x^{2}/3)}{1-x^{2}/3}}&{0\leq x<\sqrt{3}}\end{array}\right.\]
es una solución de la Ecuación\ ref {eq:2.4.10} on\((a,\sqrt3)\), donde\(a=-1/\sqrt c\) si\(c>0\) o\(a=-\infty\) si\(c\le0\). ¿Por qué esto no contradice el Teorema 2.3.1?
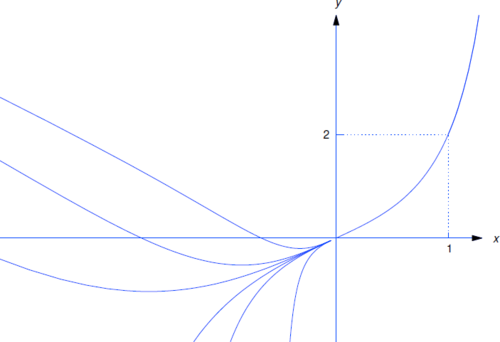
La Figura 2.4.4 muestra varias soluciones del problema del valor inicial Ecuación\ ref {eq:2.4.10}. Tenga en cuenta que estas soluciones coinciden en\((0,\sqrt{3})\).
En los dos últimos ejemplos pudimos resolver explícitamente las ecuaciones dadas. Sin embargo, esto no siempre es posible, como verás en los ejercicios.


