4.1: Crecimiento y Decaimiento
- Page ID
- 114928
Esta sección comienza con una discusión sobre el crecimiento exponencial y la decadencia, que probablemente ya hayas visto en el cálculo. Consideramos aplicaciones a la desintegración radiactiva, datación por carbono e interés compuesto. También consideramos problemas más complicados donde la tasa de cambio de una cantidad es en parte proporcional a la magnitud de la cantidad, pero también está influenciada por otros factores por ejemplo, una sustancia radiactiva se fabrica a cierta tasa, pero se descompone a una tasa proporcional a su masa, o una saver realiza depósitos regulares en una cuenta de ahorro que atraiga intereses compuestos.
Dado que las aplicaciones en esta sección tratan de funciones de tiempo, denotaremos la variable independiente por\(t\). Si\(Q\) es una función de\(t\),\(Q'\) denotará la derivada de\(Q\) con respecto a\(t\); así,
\[Q'={dQ\over dt}.\nonumber \]
Crecimiento y Decaimiento Exponencial
Uno de los modelos matemáticos más comunes para un proceso físico es el modelo exponencial, donde se asume que la tasa de cambio de una cantidad\(Q\) es proporcional a\(Q\); así
\[\label{eq:4.1.1} Q'=aQ,\]
donde\(a\) está la constante de proporcionalidad.
Del Ejemplo 2.1.3, la solución general de la Ecuación\ ref {eq:4.1.1} es
\[Q=ce^{at}\nonumber \]
y la solución del problema de valor inicial
\[Q'=aQ, \quad Q(t_0)=Q_0\nonumber \]
es
\[\label{eq:4.1.2} Q=Q_0e^{a(t-t_0)}.\]
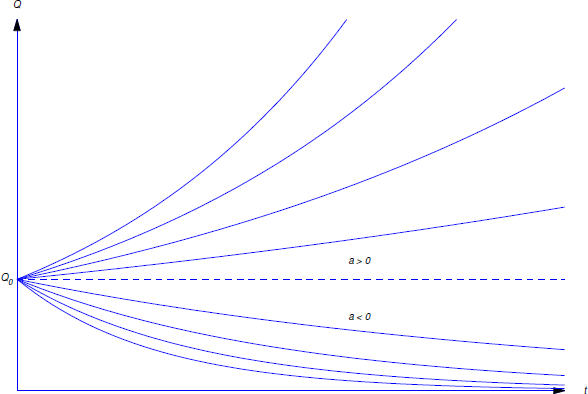
Dado que las soluciones de\(Q'=aQ\) son funciones exponenciales, decimos que una cantidad\(Q\) que satisface esta ecuación crece exponencialmente si\(a > 0\), o decae exponencialmente si\(a < 0\) (Figura 4.1.1 ).
Desintegración radiactiva
La evidencia experimental muestra que el material radiactivo se descompone a una velocidad proporcional a la masa del material presente. Según este modelo la masa\(Q(t)\) de un material radiactivo presente en el tiempo\(t\) satisface la Ecuación\ ref {eq:4.1.1}, donde\(a\) es una constante negativa cuyo valor para cualquier material dado debe ser determinado por observación experimental. Por simplicidad, reemplazaremos la constante negativa\(a\) por\(-k\), donde\(k\) hay un número positivo que llamaremos la constante de decaimiento del material. Así, la Ecuación\ ref {eq:4.1.1} se convierte
\[Q'=-kQ.\nonumber \]
Si la masa del material presente en\(t=t_0\) es\(Q_0\), la masa presente en el momento\(t\) es la solución de
\[Q'=-kQ,\quad Q(t_0)=Q_0.\nonumber \]
De la ecuación\ ref {eq:4.1.2} con\(a=-k\), la solución de este problema de valor inicial es
\[\label{eq:4.1.3} Q=Q_0e^{-k(t-t_0)}.\]
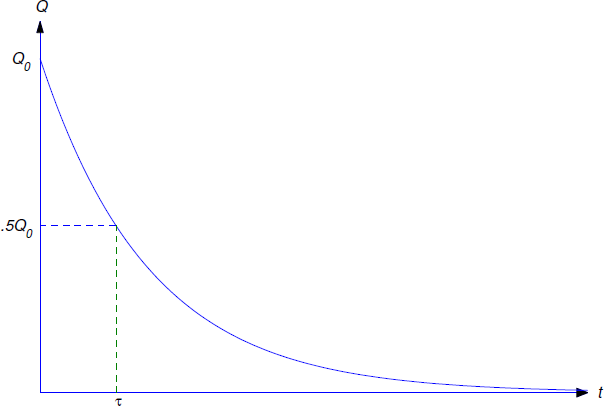
La semivida\(\tau\) de un material radiactivo se define como el tiempo requerido para que la mitad de su masa se descomponga; es decir, si\(Q(t_0)=Q_0\), entonces
\[\label{eq:4.1.4} Q(\tau+t_0)={Q_0\over 2}.\]
De la ecuación\ ref {eq:4.1.3} con\(t=\tau+t_0\), La ecuación\ ref {eq:4.1.4} es equivalente a\[Q_0e^{-k\tau}={Q_0\over 2},\nonumber \]
por lo
\[e^{-k\tau}={1\over 2}.\nonumber \]
Tomando logaritmos rendimientos
\[-k\tau=\ln{1\over 2}=-\ln2,\nonumber \]
por lo que la vida media es
\[\label{eq:4.1.5} \tau={1\over k}\ln2.\]
(Figura 4.1.2 ). La vida media es independiente\(t_0\) y\(Q_0\), ya que está determinada por las propiedades del material, no por la cantidad del material presente en un momento determinado.
Una sustancia radiactiva tiene una vida media de 1620 años.
- Si su masa es ahora de 4 g (gramos), ¿cuánto quedará dentro de 810 años?
- Encuentra el\(t_1\) momento en que quedan 1.5 g de la sustancia.
Solución a
De la ecuación\ ref {eq:4.1.3} con\(t_0=0\) y\(Q_0=4\),
\[\label{eq:4.1.6} Q=4e^{-kt},\]
donde determinamos\(k\) a partir de la Ecuación\ ref {eq:4.1.5}, con\(\tau\) = 1620 años:
\[k={\ln2\over\tau}={\ln2\over 1620}. \nonumber\]
Sustituyendo esto en la Ecuación\ ref {eq:4.1.6} rendimientos
\[\label{eq:4.1.7} Q=4e^{-(t\ln2)/1620}.\]
Por lo tanto la masa que queda después de 810 años será
\[\begin{array}{rl} Q(810) &=4e^{-(810\ln2)/1620}=4e^{-(\ln2)/2} \\ &=2\sqrt{2} \mbox{ g}. \end{array}\nonumber \]
Solución b
Ajuste\(t=t_1\) en Ecuación\ ref {eq:4.1.7} y requiriendo que\(Q(t_1)=1.5\) rinde
\[{3\over2}=4e^{(-t_1\ln2)/1620}. \nonumber\]
Dividiendo por 4 y tomando logaritmos rendimientos
\[\ln{3\over8}=-{t_1\ln2\over1620}. \nonumber\]
Dado que\(\ln3/8=-\ln8/3\),
\[t_1=1620{\ln8/3\over\ln2}\approx 2292.4\;\mbox{ years}. \nonumber\]
Intereses Acompuestos Continuamente
Supongamos que depositamos una cantidad de dinero\(Q_0\) en una cuenta que devenga intereses y no hacemos más depósitos o retiros por\(t\) años, durante los cuales la cuenta tiene intereses a una tasa anual constante\(r\). Para calcular el valor de la cuenta al final de los\(t\) años, necesitamos una información más: cómo se agrega el interés a la cuenta, o —como dicen los banqueros— cómo se agrava. Si el interés se compone anualmente, el valor de la cuenta se multiplica por\(1+r\) al final de cada año. Esto quiere decir que después de\(t\) años el valor de la cuenta es
\[Q(t)=Q_0(1+r)^t. \nonumber \]
Si los intereses se componen semestralmente, el valor de la cuenta se multiplica por\((1+r/2)\) cada 6 meses. Dado que esto ocurre dos veces al año, el valor de la cuenta después de\(t\) años es
\[Q(t)=Q_0\left(1+{r\over 2}\right)^{2t}. \nonumber \]
En general, si el interés se compone\(n\) veces al año, el valor de la cuenta se multiplica\(n\) veces al año por\((1+r/n)\); por lo tanto, el valor de la cuenta después de\(t\) años es
\[\label{eq:4.1.8} Q(t)=Q_0\left(1+{r\over n}\right)^{nt}. \]
De esta manera, al aumentar la frecuencia de capitalización se incrementa el valor de la cuenta después de un periodo de tiempo fijo. El cuadro 4.1.1 muestra el efecto de incrementar el número de compuestos a lo largo de los\(t=5\) años sobre un depósito inicial de\(Q_0=100\) (dólares), a una tasa de interés anual del 6%.
| \(n\)(número de compuestos por año) | \($100\left(1+\frac{.06}{n} \right)^{5n}\)(valor en dólares después de 5 años) |
|---|---|
| \ (n\) (número de compuestos por año) ">1 | \ ($100\ left (1+\ frac {.06} {n}\ right) ^ {5n}\) (valor en dólares después de 5 años) ">$133.82 |
| \ (n\) (número de compuestos por año) ">2 | \ ($100\ left (1+\ frac {.06} {n}\ right) ^ {5n}\) (valor en dólares después de 5 años) ">$134.39 |
| \ (n\) (número de compuestos por año) ">4 | \ ($100\ left (1+\ frac {.06} {n}\ right) ^ {5n}\) (valor en dólares después de 5 años) ">$134.68 |
| \ (n\) (número de compuestos por año) ">8 | \ ($100\ left (1+\ frac {.06} {n}\ right) ^ {5n}\) (valor en dólares después de 5 años) ">$134.83 |
| \ (n\) (número de compuestos por año) ">364 | \ ($100\ left (1+\ frac {.06} {n}\ right) ^ {5n}\) (valor en dólares después de 5 años) ">$134.98 |
Puede ver en la Tabla 4.1.1 que el valor de la cuenta después de 5 años es una función creciente de\(n\). Ahora supongamos que la tasa de interés máxima permitida en las cuentas de ahorro está restringida por ley, pero los intervalos de tiempo entre sucesivos compuestos no lo son; entonces los bancos competidores pueden atraer ahorradores al componer a menudo. El último paso en esta dirección es componerse continuamente, con lo cual queremos decir que\(n\to\infty\) en la Ecuación\ ref {eq:4.1.8}. Ya que sabemos por cálculo que
\[\lim_{n\to\infty} \left(1+{r\over n}\right)^n=e^r, \nonumber\]
esto rinde
\[\begin{array}{rl} Q(t) & =\lim_{n\to\infty} Q_0\left(1+{r\over n}\right)^{nt}=Q_0 \left[ \lim_{n\to\infty} \left(1+{r\over n}\right)^n\right]^t \\[12pt] &=Q_0e^{rt}. \end{array} \nonumber \]
Observe que\(Q=Q_0e^{rt}\) es la solución del problema de valor inicial
\[Q'=rQ, \quad Q(0)=Q_0; \nonumber\]
es decir, con la continua capitalización el valor de la cuenta crece exponencialmente.
Si se depositan $150 en un banco que paga\(5{1\over2}\)% de interés anual compuesto continuamente, el valor de la cuenta después de\(t\) años es
\[Q(t)=150e^{.055t} \nonumber\]
dólares. (Tenga en cuenta que es necesario escribir la tasa de interés como decimal; así,\(r=.055\).) Por lo tanto, después de\(t=10\) años el valor de la cuenta es
\[Q(10)=150e^{.55} \approx \$259.99. \nonumber\]
Deseamos acumular $10,000 en 10 años haciendo un solo depósito en una cuenta de ahorros con\(5{1\over2}\)% de interés anual compuesto continuamente. ¿Cuánto debemos depositar en la cuenta?
Solución
El valor de la cuenta en el momento\(t\) es
\[\label{eq:4.1.9} Q(t)=Q_0e^{.055t}.\]
Como queremos\(Q(10)\) ser de $10,000, el depósito inicial\(Q_0\) debe satisfacer la ecuación
\[\label{eq:4.1.10} 10000=Q_0e^{.55},\]
obtenido por ajuste\(t=10\) y\(Q(10)=10000\) en Ecuación\ ref {eq:4.1.9}. Resolviendo la ecuación\ ref {eq:4.1.10} para\(Q_0\) rendimientos
\[Q_0=10000e^{-.55} \approx \$5769.50.\nonumber \]
Crecimiento y Decaimiento Mixto
Una sustancia radiactiva con constante de desintegración\(k\) se produce a una tasa constante de\(a\) unidades de masa por unidad de tiempo.
- Suponiendo eso\(Q(0)=Q_0\), encontrar la masa\(Q(t)\) de la sustancia presente en el momento\(t\).
- Encontrar\(\lim_{t\to\infty} Q(t)\).
Solución a:
Aquí
\[Q'=\mbox{ rate of increase of } Q - \mbox{ rate of decrease of } Q.\nonumber \]
La tasa de incremento es la constante\(a\). Dado que\(Q\) es radiactivo con constante de desintegración\(k\), la tasa de disminución es\(kQ\). Por lo tanto
\[Q'=a-kQ.\nonumber \]
Esta es una ecuación diferencial lineal de primer orden. Reescribirlo e imponer la condición inicial muestra que\(Q\) es la solución del problema del valor inicial
\[\label{eq:4.1.11} Q'+kQ=a, \quad Q(0)=Q_0.\]
Dado que\(e^{-kt}\) es una solución de la ecuación complementaria, las soluciones de la Ecuación\ ref {eq:4.1.11} son de la forma\(Q=ue^{-kt}\), donde\(u'e^{-kt}=a\), así\(u'=ae^{kt}\). Por lo tanto,
\[u={a\over k}e^{kt}+c\nonumber \]
y
\[Q=ue^{-kt}={a\over k}+ce^{-kt}. \nonumber \]
Ya que\(Q(0)=Q_0\), estableciendo\(t=0\) aquí rendimientos
\[Q_0={a\over k}+c \quad \text{or} \quad c=Q_0-{a\over k}. \nonumber \]
Por lo tanto
\[\label{eq:4.1.12} Q={a\over k}+\left(Q_0-{a\over k}\right)e^{-kt}.\]
b. Dado que\(k > 0\),\(\lim_{t\to\infty} e^{-kt}=0\), así de la Ecuación\ ref {eq:4.1.12}
\[\lim_{t\to\infty} Q(t)={a\over k}. \nonumber \]
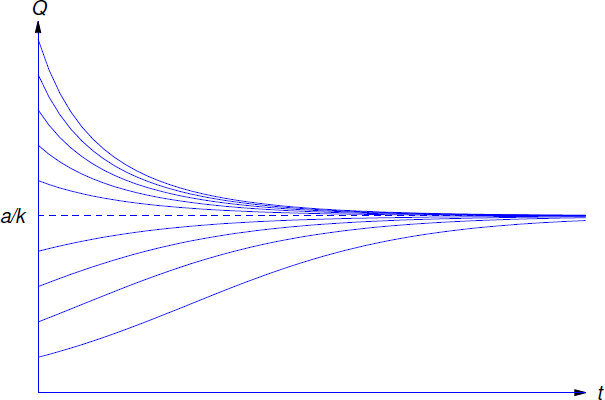
Este límite depende sólo de\(a\) y\(k\), y no de\(Q_0\). Decimos que\(a/k\) es el valor de estado estacionario de\(Q\). De la Ecuación\ ref {eq:4.1.12} también vemos que\(Q\) se acerca a su valor de estado estacionario desde arriba if\(Q_0 > a/k\), o desde abajo if\(Q_0 < a/k\). Si\(Q_0=a/k\), entonces\(Q\) permanece constante (Figura 4.1.3 ).
Datación por carbono
El hecho de que\(Q\) se acerque a un valor de estado estacionario en la situación discutida en el Ejemplo 4 subyace al método de datación por carbono, ideado por el químico estadounidense y ganador del Premio Nobel W.S. Libby.
El carbono 12 es estable, pero el carbono-14, que se produce por el bombardeo cósmico de nitrógeno en la atmósfera superior, es radiactivo con una vida media de aproximadamente 5570 años. Libby asumió que la cantidad de carbono-12 en la atmósfera ha sido constante a lo largo del tiempo, y que la cantidad de carbono radiactivo 14 alcanzó su valor de estado estacionario hace mucho tiempo como resultado de su creación y descomposición a lo largo de millones de años. Estos supuestos llevaron a Libby a concluir que la relación de carbono-14 a carbono-12 ha sido casi constante durante mucho tiempo. Esta constante, por la que denotamos\(R\), ha sido determinada experimentalmente.
Las células vivas absorben tanto el carbono-12 como el carbono-14 en la proporción en la que están presentes en el ambiente. Por lo tanto, la relación de carbono-14 a carbono-12 en una célula viva es siempre\(R\). Sin embargo, cuando la célula muere deja de absorber carbono, y la relación de carbono-14 a carbono-12 disminuye exponencialmente a medida que el carbono-14 radiactivo se descompone. Esta es la base para el método de datación por carbono, como se ilustra en el siguiente ejemplo.
Un arqueólogo que investiga el sitio de un antiguo pueblo encuentra un cementerio donde la cantidad de carbono-14 presente en los restos individuales es entre 42 y 44% de la cantidad presente en individuos vivos. Estimar la edad del pueblo y el tiempo por el que sobrevivió.
Solución
\(Q=Q(t)\)Sea la cantidad de carbono-14 en un conjunto individual de restos\(t\) años después de la muerte, y que\(Q_0\) sea la cantidad que estaría presente en individuos vivos. Dado que el carbono-14 se descompone exponencialmente con una vida media de 5570 años, su constante de descomposición es
\[k={\ln2\over 5570}. \nonumber\]
Por lo tanto
\[Q=Q_0e^{-t(\ln2)/5570}\nonumber\]
si elegimos nuestra escala de tiempo para que esa\(t_0=0\) sea la hora de la muerte. Si conocemos el valor presente de\(Q\) podemos resolver esta ecuación para\(t\), el número de años desde que ocurrió la muerte. Esto rinde
\[t=-5570 {\ln Q/Q_0\over\ln2}.\nonumber\]
Se da que\(Q=.42Q_0\) en los restos de individuos que fallecieron primero. Por lo tanto estas muertes ocurrieron sobre
\[t_1=-5570 {\ln.42\over\ln2} \approx 6971 \nonumber\]
hace años. Por las muertes más recientes,\(Q=.44 Q_0\); de ahí, estas muertes ocurrieron sobre
\[t_2=-5570 {\ln.44\over\ln2} \approx 6597 \nonumber\]
hace años. Por lo tanto, es razonable concluir que el pueblo fue fundado hace unos 7000 años, y duró unos 400 años.
Un programa de ahorro
Una persona abre una cuenta de ahorros con un depósito inicial de $1000 y posteriormente deposita $50 por semana. Encuentra el valor\(Q(t)\) de la cuenta en el momento\(t > 0\), asumiendo que el banco paga 6% de interés compuesto continuamente.
Solución
Observe que\(Q\) no es continuo, ya que hay 52 depósitos discretos por año de $50 cada uno. Para construir un modelo matemático para este problema en forma de ecuación diferencial, hacemos la suposición simplificadora de que los depósitos se realizan continuamente a una tasa de 2600 dólares anuales. Esto es esencial, ya que las soluciones de ecuaciones diferenciales son funciones continuas. Con esta suposición,\(Q\) aumenta continuamente a la tasa
\[Q'=2600+0.06 Q \nonumber\]
y por lo tanto\(Q\) satisface la ecuación diferencial
\[\label{eq:4.1.13} Q'-.06Q=2600.\]
(Por supuesto, debemos reconocer que la solución de esta ecuación es una aproximación al verdadero valor de\(Q\) en un momento dado. Discutiremos esto más adelante.) Dado que\(e^{.06t}\) es una solución de la ecuación complementaria, las soluciones de la Ecuación\ ref {eq:4.1.13} son de la forma\(Q=ue^{.06t}\), donde\(u'e^{.06t}=2600\). De ahí que\(u'=2600e^{-.06t}\),
\[u=- {2600\over.06}e^{-0.06t}+c \nonumber\]
y
\[\label{eq:4.1.14} Q=ue^{.06t}=-{2600\over.06}+ce^{.06t}.\]
Ajuste\(t=0\) y\(Q=1000\) aquí rinde
\[c=1000+{2600\over 0.06}, \nonumber\]
y sustituyendo esto en Ecuación\ ref {eq:4.1.14} rendimientos
\[\label{eq:4.1.15} Q=1000e^{.06t}+{2600\over.06}(e^{.06t}-1) \]
donde el primer plazo es el valor debido al depósito inicial y el segundo se debe a los depósitos semanales posteriores.
Se debe probar la validez de los modelos matemáticos comparando predicciones basadas en ellos con el resultado real de los experimentos. El Ejemplo 6 es inusual ya que podemos calcular el valor exacto de la cuenta en cualquier momento especificado y compararlo con el valor aproximado predicho por la Ecuación\ ref {eq:4.1.15} (Ver Ejercicio 4.1.21). En la siguiente tabla se ofrece una comparación por un periodo de diez años. Cada respuesta exacta corresponde al momento del depósito de fin de año, y se supone que cada año tiene exactamente 52 semanas.
| Año | Valor aproximado de\(Q\) (Ejemplo 4.1.6 ) | Valor exacto de\(P\) (Ejercicio 4.1.21) | Error\(Q-P\) | Porcentaje de error\((Q-P)/P\) |
|---|---|---|---|---|
| \(1\) | \ (Q\) (Ejemplo 4.1.6 ) ">\($3741.42\) | \ (P\) (Ejercicio 4.1.21) ">\($3739.87\) | \ (Q-P\) ">\($1.55\) | \ ((Q-P) /P\) ">\(.0413%\) |
| \(2\) | \ (Q\) (Ejemplo 4.1.6 ) ">\(6652.36\) | \ (P\) (Ejercicio 4.1.21) ">\(6649.17\) | \ (Q-P\) ">\(3.19\) | \ ((Q-P) /P\) ">\(.0479\) |
| \(3\) | \ (Q\) (Ejemplo 4.1.6 ) ">\(9743.30\) | \ (P\) (Ejercicio 4.1.21) ">\(9738.37\) | \ (Q-P\) ">\(4.93\) | \ ((Q-P) /P\) ">\(.0506\) |
| \(4\) | \ (Q\) (Ejemplo 4.1.6 ) ">\(13,025.38\) | \ (P\) (Ejercicio 4.1.21) ">\(13,018.60\) | \ (Q-P\) ">\(6.78\) | \ ((Q-P) /P\) ">\(.0521\) |
| \(5\) | \ (Q\) (Ejemplo 4.1.6 ) ">\(16,510.41\) | \ (P\) (Ejercicio 4.1.21) ">\(16,501.66\) | \ (Q-P\) ">\(8.75\) | \ ((Q-P) /P\) ">\(.0530\) |
| \(6\) | \ (Q\) (Ejemplo 4.1.6 ) ">\(20,210.94\) | \ (P\) (Ejercicio 4.1.21) ">\(20,200.11\) | \ (Q-P\) ">\(10.83\) | \ ((Q-P) /P\) ">\(.0536\) |
| \(7\) | \ (Q\) (Ejemplo 4.1.6 ) ">\(24,140.30\) | \ (P\) (Ejercicio 4.1.21) ">\(24,127.25\) | \ (Q-P\) ">\(13.05\) | \ ((Q-P) /P\) ">\(.0541\) |
| \(8\) | \ (Q\) (Ejemplo 4.1.6 ) ">\(28,312.63\) | \ (P\) (Ejercicio 4.1.21) ">\(28,297.23\) | \ (Q-P\) ">\(15.40\) | \ ((Q-P) /P\) ">\(.0544\) |
| \(9\) | \ (Q\) (Ejemplo 4.1.6 ) ">\(32,742.97\) | \ (P\) (Ejercicio 4.1.21) ">\(32,725.07\) | \ (Q-P\) ">\(17.90\) | \ ((Q-P) /P\) ">\(.0547\) |
| \(10\) | \ (Q\) (Ejemplo 4.1.6 ) ">\(37,447.27\) | \ (P\) (Ejercicio 4.1.21) ">\(37,426.72\) | \ (Q-P\) ">\(20.55\) | \ ((Q-P) /P\) ">\(.0549\) |


