4.2: Enfriamiento y Mezcla
- Page ID
- 114956
Ley de Refrigeración de Newton
La ley de enfriamiento de Newton establece que si un objeto con\(T(t)\) temperatura en el tiempo\(t\) está en un medio con temperatura\(T_m(t)\), la velocidad de cambio de\(T\) en el tiempo\(t\) es proporcional a\(T(t)-T_m(t)\); así,\(T\) satisface una ecuación diferencial de la forma
\[\label{eq:4.2.1} T'=-k(T-T_m).\]
Aquí\(k > 0\), ya que la temperatura del objeto debe disminuir si\(T > T_m\), o aumentar si\(T < T_m\). Llamaremos a\(k\) la constante de decaimiento de temperatura del medio.
Por simplicidad, en esta sección asumiremos que el medio se mantiene a una temperatura constante\(T_m\). Este es otro ejemplo de construcción de un modelo matemático sencillo para un fenómeno físico. Como la mayoría de los modelos matemáticos tiene sus limitaciones. Por ejemplo, es razonable suponer que la temperatura de una habitación permanece aproximadamente constante si el objeto de enfriamiento es una taza de café, pero quizás no si se trata de un enorme caldero de metal fundido. (Para más información sobre esto ver Ejercicio 4.2.17.)
Para resolver la Ecuación\ ref {eq:4.2.1}, la reescribimos como
\[T'+kT=kT_m. \nonumber\]
Dado que\(e^{-kt}\) es una solución de la ecuación complementaria, las soluciones de esta ecuación son de la forma\(T=ue^{-kt}\), donde\(u'e^{-kt}=kT_m\), así\(u'=kT_me^{kt}\). Por lo tanto,
\[u=T_me^{kt}+c, \nonumber\]
por lo
\[T=ue^{-kt}=T_m+ce^{-kt}. \nonumber\]
Si\(T(0)=T_0\), establecer\(t=0\) aquí rinde\(c=T_0-T_m\), entonces
\[\label{eq:4.2.2} T=T_m+(T_0-T_m)e^{-kt}. \]
Tenga en cuenta que\(T-T_m\) decae exponencialmente, con constante de decaimiento\(k\).
Un aislante cerámico se cuece a\(400^\circ\) C y se enfría en una habitación en la que la temperatura es\(25^\circ\) C. Después de 4 minutos la temperatura del aislador es\(200^\circ\) C. ¿Cuál es su temperatura después de 8 minutos?
Solución
Aquí\(T_0=400\) y\(T_m=25\), así la Ecuación\ ref {eq:4.2.2} se convierte
\[\label{eq:4.2.3} T=25+375e^{-kt}.\]
Determinamos\(k\) a partir de la condición señalada que\(T(4)=200\); es decir,
\[200=25+375e^{-4k}; \nonumber\]
por lo tanto,
\[e^{-4k} = {175\over 375} = {7\over 15}. \nonumber\]
Tomando logaritmos y resolviendo\(k\) rendimientos
\[k=-{1\over 4} \ln {7\over 15}={1\over 4}\ln {15\over 7}. \nonumber\]
Sustituyendo esto en la ecuación\ ref {eq:4.2.3} rendimientos
\[T=25+375 e^{-{t\over 4} \ln {15\over 7}} \nonumber\]
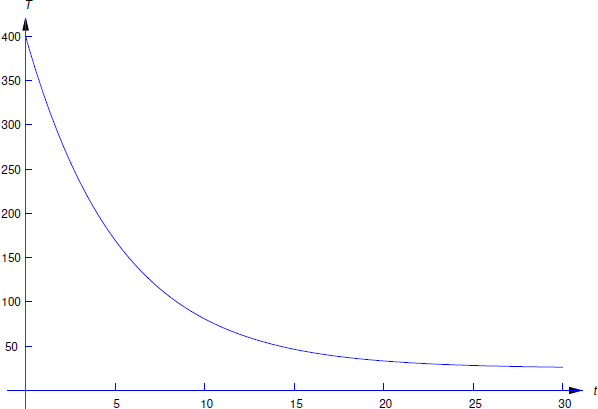
(Figura 4.2.1 ). Por lo tanto, la temperatura del aislador después de 8 minutos es
\[\begin{array}{rl} T(8) & = 25+375 e^{-2 \ln {15\over 7}} \\[9pt] & = 25+375 \left({7\over 15}\right)^2 \approx 107^\circ \mbox{C}. \end{array}\nonumber \]
Un objeto con temperatura\(72^\circ\) F se coloca afuera, donde la temperatura es\(-20^\circ\) F. A las 11:05 la temperatura del objeto es\(60^\circ\) F y a las 11:07 su temperatura es\(50^\circ\) F. ¿A qué hora se colocó el objeto afuera?
Solución
Dejar\(T(t)\) ser la temperatura del objeto a la vez\(t\). Para mayor comodidad, elegimos el origen\(t_0=0\) de la escala de tiempo para que sea 11:05 para que\(T_0=60\). Debemos determinar el\(\tau\) momento en que\(T(\tau)=72\). Sustituyendo\(T_0=60\) y\(T_m=-20\) en Ecuación\ ref {eq:4.2.2} rendimientos
\[T = -20+\bigl(60-(-20)\bigr)e^{-kt}\nonumber\]
o
\[\label{eq:4.2.4} T = -20+80e^{-kt}. \]
Obtenemos\(k\) de la condición declarada que la temperatura del objeto es de 50\(^\circ\) F a las 11:07. Ya que 11:07 está\(t=2\) en nuestra escala de tiempo, podemos determinar\(k\) sustituyendo\(T=50\) y\(t=2\) en la Ecuación\ ref {eq:4.2.4} para obtener
\[50 = -20+80e^{-2k}\nonumber\]
Esto se muestra en la Figura 4.2.2 .
Por lo tanto,
\[e^{-2k}={70\over 80}={7\over 8}.\nonumber\]
Tomando logaritmos y resolviendo\(k\) rendimientos
\[k =-{1\over 2} \ln {7\over 8} = {1\over 2} \ln {8\over 7}.\nonumber\]
Sustituyendo esto en la ecuación\ ref {eq:4.2.4} rendimientos
\[T = -20+80 e^{-{t\over 2}\ln {8\over 7}},\nonumber\]
y la condición\(T(\tau)=72\) implica que
\[72 =-20+80 e^{-{\tau\over 2} \ln {8\over 7}};\nonumber\]
por lo tanto,
\[e^{-{\tau\over 2} \ln {8\over 7}} ={92\over 80} = {23\over 20}.\nonumber\]
Tomando logaritmos y resolviendo\(\tau\) rendimientos
\[\tau = -{2 \ln {23\over 20}\over \ln {8\over 7}} \approx-2.09\ \mbox{min}.\nonumber\]
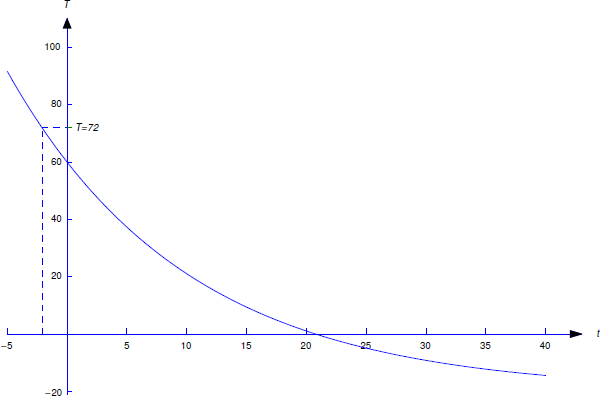
Por lo tanto el objeto se colocó afuera aproximadamente 2 minutos y 5 segundos antes de las 11:05; es decir, a las 11:02:55.
Problemas de mezcla
En los dos ejemplos siguientes se agrega una solución de agua salada con una concentración dada (peso de sal por unidad de volumen de solución) a una velocidad especificada a un tanque que inicialmente contiene agua salada con una concentración diferente. El problema es determinar la cantidad de sal en el tanque en función del tiempo. Este es un ejemplo de un problema de mezcla. Para construir un modelo matemático tratable para problemas de mezcla asumimos en nuestros ejemplos (y la mayoría de los ejercicios) que la mezcla se agita instantáneamente para que la sal esté siempre distribuida uniformemente por toda la mezcla. Los ejercicios 4.2.22 y 4.2.23 tratan situaciones en las que esto no es así, pero la distribución de la sal se vuelve aproximadamente uniforme como\(t\to\infty\).
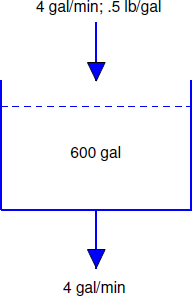
Un tanque inicialmente contiene 40 libras de sal disuelta en 600 galones de agua. A partir de\(t_0 = 0\), el agua que contiene 1/2 libra de sal por galón se vierte en el tanque a razón de 4 gal/min y la mezcla se drena del tanque a la misma velocidad (Figura 4.2.3 ).
- Encuentre una ecuación diferencial para la cantidad\(Q(t)\) de sal en el tanque en el momento\(t > 0\), y resuelva la ecuación para determinar\(Q(t)\).
- Encontrar\(\lim_{t\to\infty}Q(t)\).
Solución a
Para encontrar una ecuación diferencial para\(Q\), debemos usar la información dada para derivar una expresión para\(Q'\). Pero\(Q'\) es la tasa de cambio de la cantidad de sal en el tanque cambia con respecto al tiempo; así, si tasa in denota la velocidad a la que la sal ingresa al tanque y la tasa de salida denota la velocidad por la que sale, entonces
\[\label{eq:4.2.5} Q' = \mbox{rate in}-\mbox{rate out}.\]
La tasa en es
\[\left({1\over 2}\ \mbox{lb/gal}\right) \times (4\ \mbox{gal/min}) = 2\ \mbox{lb/min}.\nonumber\]
Determinar la tasa de salida requiere un poco más de reflexión. Estamos retirando 4 galones de la mezcla por minuto, y siempre hay 600 galones en el tanque; es decir, estamos retirando\(1/150\) la mezcla por minuto. Dado que la sal se distribuye uniformemente en la mezcla, también estamos retirando\(1/150\) de la sal por minuto. Por lo tanto, si hay\(Q(t)\) libras de sal en el tanque en el momento\(t\), la tasa de salida en cualquier momento\(t\) es\(Q(t)/150\). Alternativamente, podemos llegar a esta conclusión argumentando que
\[\begin{align*} \mbox{rate out} & = (\mbox{concentration})\times(\mbox{rate of flow out}) \\[5pt] &= (\mbox{lb/gal})\times(\mbox{gal/min})\\[4pt] &= {Q(t)\over600} \times 4 \\[4pt] &={Q(t)\over150}. \end{align*}\nonumber \]
Ahora podemos escribir la Ecuación\ ref {eq:4.2.5} como
\[Q' = 2-{Q\over 150}. \nonumber\]
Esta ecuación de primer orden se puede reescribir como
\[Q'+{Q\over 150} = 2. \nonumber\]
Dado que\(e^{-t/150}\) es una solución de la ecuación complementaria, las soluciones de esta ecuación son de la forma\(Q=ue^{-t/150}\), donde\(u'e^{-t/150}=2\), así\(u'=2e^{t/150}\). Por lo tanto,
\[u = 300e^{t/150}+c, \nonumber\]
por lo
\[\label{eq:4.2.6} Q=ue^{-t/150}=300+ce^{-t/150}\]
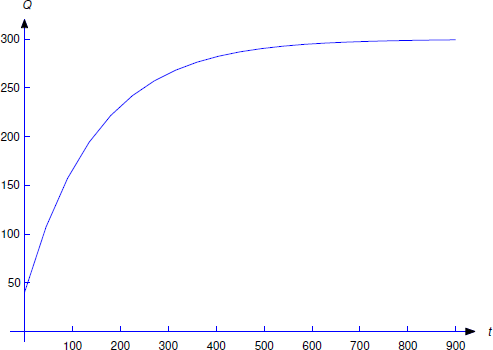
(Figura 4.2.4 ). Dado que\(Q(0)=40\),\(c=-260\); por lo tanto,
\[Q=300-260e^{-t/150}.\nonumber\]
Solución b
De la Ecuación\ ref {eq:4.2.6}, vemos que eso\(\lim_{t \to \infty}Q(t)=300\) para cualquier valor de\(Q(0)\). Esto es intuitivamente razonable, ya que la solución entrante contiene 1/2 libra de sal por galón y siempre hay 600 galones de agua en el tanque.
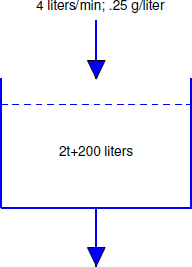
Un tanque de 500 litros contiene inicialmente 10 g de sal disuelta en 200 litros de agua. A partir de\(t_0=0\), se vierte en el tanque agua que contiene 1/4 g de sal por litro a razón de 4 litros/min y la mezcla se drena del tanque a razón de 2 litros/min (Figura [figura:4.2.5}). Encuentre una ecuación diferencial para la cantidad\(Q(t)\) de sal en el tanque en el momento\(t\) anterior al momento en que el tanque se desborda y encuentre la concentración\(K(t)\) (g/litro) de sal en el tanque en cualquier momento.
Solución
Primero determinamos la cantidad\(W(t)\) de solución en el tanque en cualquier momento\(t\) antes del desbordamiento. Ya que\(W(0) = 200\) y estamos agregando 4 litros/min mientras eliminamos solo 2 litros/min, hay una ganancia neta de 2 litros/min en el tanque; por lo tanto,
\[W(t) = 2t+200.\nonumber\]
Desde\(W(150)=500\) litros (capacidad del tanque), esta fórmula es válida para\(0 \le t \le 150\).
Ahora deja\(Q(t)\) ser el número de gramos de sal en el tanque a la hora\(t\), dónde\(0 \le t \le 150\). Como en el Ejemplo 4.2.3
\[\label{eq:4.2.7} Q' = \mbox{rate in}-\mbox{rate out}.\]
La tasa en es
\[\label{eq:4.2.8} \left({1\over 4}\ \mbox{g/liter}\,\right) \times (4\ \mbox{liters/min}\,) = 1\ \mbox{g/min}.\]
Para determinar la tasa de salida, observamos que dado que la mezcla se está retirando del tanque a una velocidad constante de 2 litros/min y hay\(2t+200\) litros en el tanque a la vez\(t\), la fracción de la mezcla que se retira por minuto a la vez\(t\) es
\[{2\over 2t+200} = {1\over t+100}.\nonumber\]
Estamos retirando esta misma fracción de la sal por minuto. Por lo tanto, dado que en el momento hay\(Q(t)\) gramos de sal en el tanque\(t\),
\[\label{eq:4.2.9} \mbox{rate out} = {Q(t)\over t+100}.\]
Alternativamente, podemos llegar a esta conclusión argumentando que
\[\begin{array}{lcl} \mbox{rate out} & = & (\mbox{concentration})\times(\mbox{rate of flow out}) =(\mbox{g/liter})\times(\mbox{liters/min})\\[10pt] &=&{Q(t)\over2t+200}\times 2={Q(t)\over t+100}. \end{array} \nonumber \]
Sustituyendo la ecuación\ ref {eq:4.2.8} y la ecuación\ ref {eq:4.2.9} en la ecuación\ ref {eq:4.2.7} rendimientos
\[\label{eq:4.2.10} Q'=1-{Q\over t+100},\quad \text{so} \quad Q'+{1\over t+100} Q=1.\]
Por separación de variables,\(1/(t+100)\) es una solución de la ecuación complementaria, por lo que las soluciones de la Ecuación\ ref {eq:4.2.10} son de la forma
\[Q={u\over t+100}, \quad \text{where} \quad {u'\over t+100 =1}, \quad \text{so} \quad u'=t+100.\nonumber\]
Por lo tanto,
\[\label{eq:4.2.11} u = {(t+100)^2\over 2}+c.\]
Dado que\(Q(0)=10\) y\(u=(t+100)Q\), Ecuación\ ref {eq:4.2.11} implica que
\[(100)(10) = {(100)^2\over 2}+c,\nonumber\]
por lo
\[c=100(10)-{(100)^2\over 2} =-4000\nonumber\]
y por lo tanto
\[u = {(t+100)^2\over 2} -4000.\nonumber\]
Por lo tanto,
\[Q = {u\over t+200}= {t+100\over 2}-{4000\over t+100}.\nonumber\]
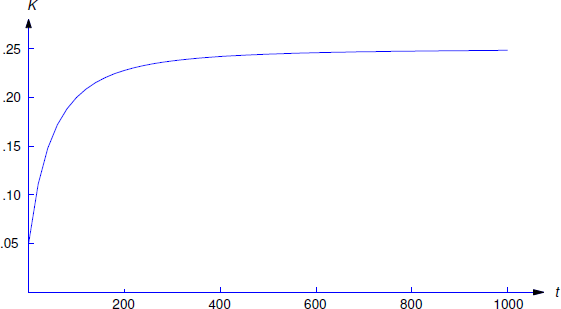
Ahora deja\(K(t)\) ser la concentración de sal a la vez\(t\). Entonces
\[K(t) = {1\over 4}-{2000\over(t+100)^2}\nonumber\]
Esto se muestra en la Figura 4.2.6 .