4.3: Mecánica Primaria

Última actualización
Guardar como PDF

Page ID: 114973

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Segunda Ley del Movimiento de Newton

En esta sección consideramos un objeto con masa constante que\(m\) se mueve a lo largo de una línea bajo una fuerza\(F\). Dejar\(y=y(t)\) ser el desplazamiento del objeto desde un punto de referencia en la línea en el momento\(t\), y dejar\(v=v(t)\) y\(a=a(t)\) ser la velocidad y aceleración del objeto en el momento\(t\). Así,\(v=y'\) y\(a=v'=y''\), donde el primo denota diferenciación con respecto a\(t\). La segunda ley del movimiento de Newton afirma que la fuerza\(F\) y la aceleración\(a\) están relacionadas por la ecuación

\[\label{eq:4.3.1} F=ma.\]

Nota: Unidades

En aplicaciones hay tres conjuntos principales de unidades en uso para longitud, masa, fuerza y tiempo: los sistemas cgs, mks y británicos. Los tres usan el segundo como unidad de tiempo. El cuadro 4.3.1 muestra las otras unidades. Consistente con la Ecuación\ ref {eq:4.3.1}, la unidad de fuerza en cada sistema se define como la fuerza requerida para impartir una aceleración de (una unidad de longitud)\(/s^2\) a una unidad de masa.

Tabla 4.3.1
Set	Largo	Fuerza	Masa
cgs	centímetro (cm)	dinas (d)	gramo (g)
mks	metro (m)	Newton (N)	kilogramo (kg)
Británicos	pie (ft)	libra (lb)	babosa (sl)

Si asumimos que la Tierra es una esfera perfecta con densidad de masa constante, la ley de gravitación de Newton (discutida más adelante en esta sección) afirma que la fuerza ejercida sobre un objeto por el campo gravitacional de la Tierra es proporcional a la masa del objeto e inversamente proporcional al cuadrado de su distancia desde el centro de la Tierra. Sin embargo, si el objeto permanece lo suficientemente cerca de la superficie de la Tierra, podemos suponer que la fuerza gravitacional es constante e igual a su valor en la superficie. La magnitud de esta fuerza es\(mg\), donde\(g\) se llama la aceleración debido a la gravedad. (Para ser completamente precisos,\(g\) debería llamarse la magnitud de la aceleración debida a la gravedad en la superficie de la Tierra.) Esta cantidad ha sido determinada experimentalmente. Valores aproximados de\(g\) son

\[\begin{array}{rl} g &=980\ \mbox{cm/s}^2 \hskip40pt \mbox{(cgs)} \\ g &=9.8\ \mbox{m/s}^2 \hskip48pt \mbox{(mks)} \\ g &=32\ \mbox{ft/s}^2 \hskip52pt \mbox{(British)}. \end{array}\nonumber \]

En general, la fuerza\(F\) en la Ecuación\ ref {eq:4.3.1} puede depender de\(t\),\(y\), y\(y'\). Ya que\(a=y''\), la ecuación\ ref {eq:4.3.1} se puede escribir en la forma

\[\label{eq:4.3.2} my''=F(t,y,y'),\]

que es una ecuación de segundo orden. Consideraremos esta ecuación con restricciones\(F\) más adelante; sin embargo, dado que el Capítulo 2 se ocupó únicamente de ecuaciones de primer orden, consideramos aquí solo problemas en los que la Ecuación\ ref {eq:4.3.2} puede ser refundida como una ecuación de primer orden. Esto es posible si\(F\) no depende de\(y\), por lo que la Ecuación\ ref {eq:4.3.2} es de la forma

\[my''=F(t,y'). \nonumber \]

Dejar\(v=y'\) y\(v'=y''\) producir una ecuación de primer orden para\(v\):

\[\label{eq:4.3.3} mv'=F(t,v).\]

Resolver esta ecuación\(v\) rinde en función de\(t\). Si sabemos desde\(y(t_0)\) hace algún tiempo\(t_0\), podemos integrarnos\(v\) para obtener\(y\) en función de\(t\).

Las ecuaciones de la forma Ecuación\ ref {eq:4.3.3} ocurren en problemas que involucran movimiento a través de un medio de resistencia.

Movimiento a través de un medio de resistencia bajo fuerza gravitacional constante

Ahora consideramos un objeto que se mueve verticalmente en algún medio. Suponemos que las únicas fuerzas que actúan sobre el objeto son la gravedad y la resistencia del medio. También asumimos que el movimiento tiene lugar cerca de la superficie de la Tierra y toma la dirección ascendente para ser positivo, por lo que se puede suponer que la fuerza gravitacional tiene el valor constante\(-mg\). Veremos que, bajo supuestos razonables sobre la fuerza de resistencia, la velocidad se acerca a un límite como\(t\to\infty\). Llamamos a este límite la velocidad terminal.

Ejemplo 4.3.1

Un objeto con masa\(m\) se mueve bajo una fuerza gravitacional constante a través de un medio que ejerce una resistencia con magnitud proporcional a la velocidad del objeto. (Recordemos que la velocidad de un objeto es\(|v|\), el valor absoluto de su velocidad\(v\).) Encuentra la velocidad del objeto en función de\(t\), y encuentra la velocidad terminal. Supongamos que la velocidad inicial es\(v_0\).

Solución

La fuerza total que actúa sobre el objeto es

\[\label{eq:4.3.4} F=-mg+F_1,\]

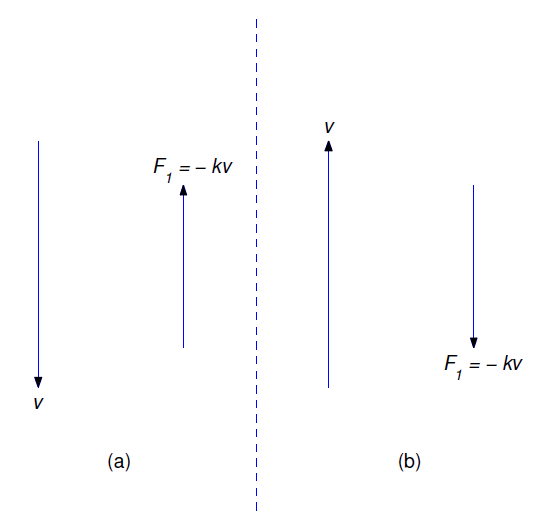
donde\(-mg\) está la fuerza debida a la gravedad y\(F_1\) es la fuerza de resistencia del medio, que tiene magnitud\(k|v|\), donde\(k\) es una constante positiva. Si el objeto se mueve hacia abajo (\(v\le 0\)), la fuerza de resistencia es hacia arriba (Figura 4.3.1a ), entonces

\[F_1=k|v|=k(-v)=-kv. \nonumber \]

Por otro lado, si el objeto se mueve hacia arriba (\(v\ge 0\)), la fuerza de resistencia es hacia abajo (Figura 4.3.1b , entonces

\[F_1=-k|v|=-kv.\nonumber\]

Así, la ecuación\ ref {eq:4.3.4} puede escribirse como

\[\label{eq:4.3.5} F=-mg-kv,\]

independientemente del signo de la velocidad.

De la segunda ley de movimiento de Newton,

\[F=ma=mv',\nonumber\]

así Ecuación\ ref {eq:4.3.5} rendimientos

\[mv'=-mg-kv,\nonumber\]

\[\label{eq:4.3.6} v'+{k\over m}v=-g.\]

Dado que\(e^{-kt/m}\) es una solución de la ecuación complementaria, las soluciones de la Ecuación\ ref {eq:4.3.6} son de la forma\(v=ue^{-kt/m}\), donde\(u'e^{-kt/m}=-g\), así\(u'=-ge^{kt/m}\). Por lo tanto,

\[u=-{mg\over k} e^{kt/m}+c,\nonumber\]

por lo

\[\label{eq:4.3.7} v=ue^{-kt/m}=-{mg\over k}+ce^{-kt/m}.\]

Ya que\(v(0)=v_0\),\[v_0=-{mg\over k}+c,\nonumber\] así

\[c=v_0+{mg\over k}\nonumber\]

y la Ecuación\ ref {eq:4.3.7} se convierte

\[v=-{mg\over k}+\left(v_0+{mg\over k}\right) e^{-kt/m}.\nonumber\]

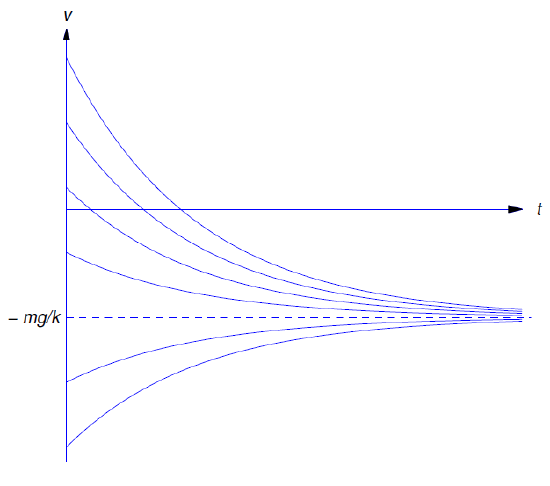
Dejar\(t\to\infty\) aquí muestra que la velocidad terminal es

\[\lim_{t\to\infty} v(t)=-{mg\over k},\nonumber\]

que es independiente de la velocidad inicial\(v_0\) (Figura 4.3.2 ).

Soluciones de Mv' = -mg - kv — Figura 4.3.2 : Soluciones de\(mv'=-mg-kv\)

Ejemplo 4.3.2 : Velocidad terminal

A un objeto de 960-lb se le da una velocidad ascendente inicial de 60 pies/s cerca de la superficie de la Tierra. La atmósfera resiste el movimiento con una fuerza de 3 lb por cada pies/s de velocidad. Suponiendo que la única otra fuerza que actúa sobre el objeto es la gravedad constante, encuentra su velocidad\(v\) en función de\(t\), y encuentra su velocidad terminal.

Solución

Desde\(mg=960\) y\(g=32\),\(m=960/32=30\). La resistencia atmosférica es\(-3v\) lb si\(v\) se expresa en pies por segundo. Por lo tanto

\[30v'=-960-3v,\nonumber\]

que reescribimos como\[v'+{1\over 10}v=-32.\nonumber\]

Dado que\(e^{-t/10}\) es una solución de la ecuación complementaria, las soluciones de esta ecuación son de la forma\(v=ue^{-t/10}\), donde\(u'e^{-t/10}=-32\), así\(u'=-32e^{t/10}\). Por lo tanto,

\[u=-320 e^{t/10}+c,\nonumber\]

por lo

\[\label{eq:4.3.8} v=ue^{-t/10}=-320+ce^{-t/10}.\]

La velocidad inicial es de 60 pies/s en la dirección ascendente (positiva); por lo tanto,\(v_0=60\). Sustituyendo\(t=0\) y\(v=60\) en Ecuación\ ref {eq:4.3.8} rendimientos

\[60=-320+c,\nonumber\]

así\(c=380\), y la Ecuación\ ref {eq:4.3.8} se convierte

\[v=-320+380e^{-t/10}\ \mbox{ft/s}\nonumber\]

La velocidad terminal es

\[\lim_{t\to\infty}v(t)=-320\mbox{ ft/s.}\nonumber\]

Ejemplo 4.3.3

A una masa de 10 kg se le da una velocidad inicial\(v_0\le0\) cerca de la superficie de la Tierra. Las únicas fuerzas que actúan sobre él son la gravedad y la resistencia atmosférica proporcionales al cuadrado de la velocidad. Suponiendo que la resistencia es de 8 N si la velocidad es de 2 m/s, encuentra la velocidad del objeto en función de\(t\), y encuentra la velocidad terminal.

Solución

Dado que el objeto está cayendo, la resistencia está en dirección ascendente (positiva). Por lo tanto,

\[\label{eq:4.3.9} mv'=-mg+kv^2,\]

donde\(k\) es una constante. Dado que la magnitud de la resistencia es de 8 N cuando\(v=2\) m/s,

\[k(2^2)=8, \nonumber \]

así\(k=2\ \mbox{N-s}^2/\mbox{m}^2\). Desde\(m=10\) y\(g=9.8\), Ecuación\ ref {eq:4.3.9} se convierte

\[\label{eq:4.3.10} 10v'=-98+2v^2=2(v^2-49).\]

Si\(v_0=-7\), entonces\(v\equiv-7\) para todos\(t\ge0\). Si\(v_0\ne-7\), separamos las variables para obtener

\[\label{eq:4.3.11} {1\over v^2-49}v'={1\over5},\]

lo cual es conveniente para la expansión de fracción parcial requerida

\[\label{eq:4.3.12} \frac{1}{v^2-49} =\frac{1}{(v-7)(v+7)} ={1\over 14}\left[{1\over v-7} -{1\over v+7}\right].\]

Sustituyendo la ecuación\ ref {eq:4.3.12} en Ecuación\ ref {eq:4.3.11} rendimientos

\[{1\over14}\left[{1\over v-7}-{1\over v+7}\right]v'={1\over5},\nonumber\]

por lo

\[\left[{1\over v-7}-{1\over v+7}\right]v'={14\over5}.\nonumber\]

Integrando estos rendimientos

\[\ln |v-7|-\ln|v+7|=14t/5+k.\nonumber\]

Por lo tanto

\[\left|{v-7\over v+7}\right|=e^ke^{14t/5}.\nonumber\]

Desde Teorema 2.3.1 implica que\((v-7)/(v+7)\) no se puede cambiar de signo (¿por qué?) , podemos reescribir la última ecuación como

\[\label{eq:4.3.13} {v-7\over v+7}=ce^{14t/5},\]

que es una solución implícita de la Ecuación\ ref {eq:4.3.10}. Resolviendo esto para\(v\) rendimientos

\[\label{eq:4.3.14} v=-7{c+e^{-14t/5}\over c-e^{-14t/5}}.\]

Ya que\(v(0)=v_0\), la ecuación\ ref {eq:4.3.13} implica que

\[c={v_0-7\over v_0+7}.\nonumber\]

Sustituyendo esto en la Ecuación\ ref {eq:4.3.14} y simplificar los rendimientos

\[v=-7{v_0(1+e^{-14t/5}-7(1-e^{-14t/5}\over v_0(1-e^{-14t/5}-7(1+e^{-14t/5}}.\nonumber\]

Ya que\(v_0\le0\),\(v\) está definido y negativo para todos\(t>0\). La velocidad terminal es

\[\lim_{t\to\infty} v(t)=-7\ \mbox{m/s},\nonumber\]

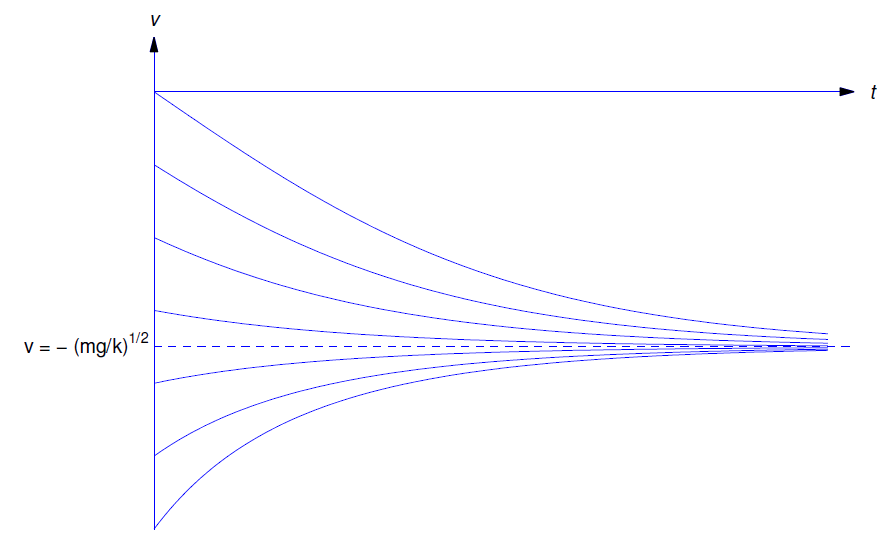
independiente de\(v_0\). De manera más general, se puede demostrar (Ejercicio 4.3.11) que si\(v\) hay alguna solución de la Ecuación\ ref {eq:4.3.9} tal que\(v_0\le0\) entonces

\[\lim_{t\to\infty}v(t)=-\sqrt{mg\over k}. \nonumber\]

Esto se demuestra en la Figura 4.3.3 .

Soluciones de mv'=-mg+kv^2,\ v (0) =v_0\ le0 — Figura 4.3.3 : Soluciones de\(mv'=-mg+kv^2,\ v(0)=v_0\le0\)

Ejemplo 4.3.4

Una masa de 10 kg se lanza verticalmente hacia arriba desde la superficie de la Tierra con una velocidad inicial de\(v_0\) m/s Las únicas fuerzas que actúan sobre la masa son la gravedad y la resistencia atmosférica proporcional al cuadrado de la velocidad. Suponiendo que la resistencia atmosférica es de 8 N si la velocidad es de 2 m/s, encuentre el tiempo\(T\) requerido para que la masa alcance la altitud máxima.

Solución

La masa subirá mientras\(v>0\) y alcanzará su altitud máxima cuando\(v=0\). Por lo tanto\(v>0\) para\(0\leq t<T\) y\(v(T)=0\); por lo tanto, sustituimos la Ecuación\ ref {eq:4.3.10} por

\[\label{eq:4.3.15} 10v'=-98-2v^2.\]

Separación de rendimientos de variables

\[{5\over v^2+49}v'=-1,\nonumber\]

e integrando estos rendimientos

\[{5\over7}\tan^{-1}{v\over7}=-t+c.\nonumber\]

(Recordemos que\(\tan^{-1}u\) es el número\(\theta\) tal que\(-\pi/2 < \theta < \pi/2\) y\(\tan \theta=u\).) Dado que\(v(0)=v_0\),

\[c={5\over7}\tan^{-1}{v_0\over7},\nonumber\]

así\(v\) se define implícitamente por\[\label{eq:4.3.16} {5\over7} \tan^{-1}{v\over7}=-t+{5\over7} \tan^{-1}{v_0\over7}, \quad 0\le t\le T.\]

Resolviendo esto para\(v\) rendimientos

\[\label{eq:4.3.17} v=7\tan\left(-{7t\over5}+\tan^{-1}{v_0\over7}\right).\]

Uso de la identidad

\[\tan(A-B)={\tan A-\tan B\over1+\tan A\tan B}\nonumber\]

con\(A=\tan^{-1}(v_0/7)\) y\(B=7t/5\), y señalando que\(\tan(\tan^{-1}\theta)=\theta\), podemos simplificar la Ecuación\ ref {eq:4.3.17} a

\[v=7{v_0-7\tan(7t/5)\over7+v_0\tan(7t/5)}.\nonumber\]

Dado que\(v(T)=0\) y\(\tan^{-1}(0)=0\), Ecuación\ ref {eq:4.3.16} implica que

\[-T+{5\over7} \tan^{-1}{v_0\over7}=0.\nonumber\]

Por lo tanto

\[T={5\over7} \tan^{-1}{v_0\over7}.\nonumber\]

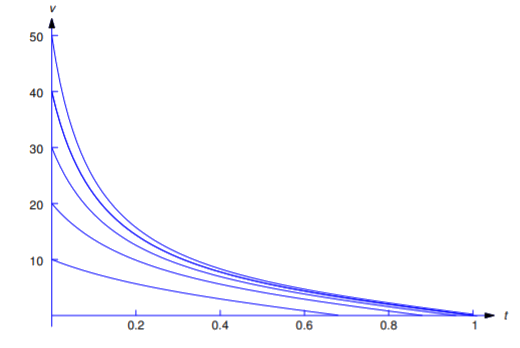
Ya que\(\tan^{-1}(v_0/7)<\pi/2\) para todos\(v_0\), el tiempo requerido para que la masa alcance su altitud máxima es menor que

\[{5\pi\over 14} \approx 1.122\ \mbox{s}\nonumber\]

independientemente de la velocidad inicial. La figura 4.3.4 muestra gráficas de\(v\) más\([0,T]\) para varios valores de\(v_0\).

Figura 4.3.4 : Soluciones de 4.3.15 para varios\(v_{0}>0\)

Velocidad de escape

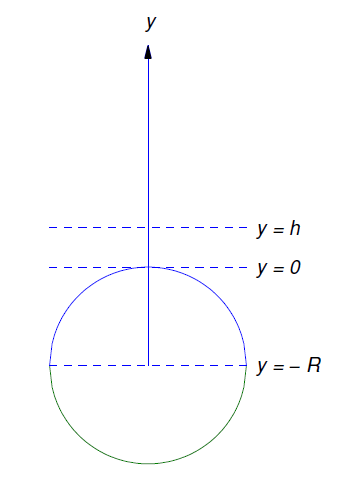
Supongamos que un vehículo espacial es lanzado verticalmente y su combustible se agota cuando el vehículo alcanza una altitud\(h\) sobre la Tierra, donde\(h\) es lo suficientemente grande para que se pueda descuidar la resistencia debida a la atmósfera terrestre. Deja\(t=0\) ser el momento en que se produce el burnout. Suponiendo que se puedan descuidar las fuerzas gravitacionales de todos los demás cuerpos celestes, el movimiento del vehículo para\(t > 0\) es el de un objeto con masa constante\(m\) bajo la influencia de la fuerza gravitacional de la Tierra, que ahora asumimos que varía inversamente con el cuadrado de la distancia de la Tierra” s centro; así, si tomamos la dirección ascendente para ser positivos entonces la fuerza gravitacional sobre el vehículo a una altitud\(y\) sobre la Tierra es

\[\label{eq:4.3.18} F=-{K\over(y+R)^2},\]

donde\(R\) está el radio de la Tierra (Figura 4.3.5 ).

Desde\(F=-mg\) cuándo\(y=0\), establecer\(y=0\) en la ecuación\ ref {eq:4.3.18} rendimientos

\[-mg=-{K\over R^2};\nonumber\]

por lo tanto\(K=mgR^2\) y la Ecuación\ ref {eq:4.3.18} se puede escribir más específicamente como

\[\label{eq:4.3.19} F=-{mgR^2\over(y+R)^2}.\]

De la segunda ley de movimiento de Newton,

\[F=m{d^2y\over dt^2},\nonumber\]

así que la ecuación\ ref {eq:4.3.19} implica que

\[\label{eq:4.3.20} {d^2y\over dt^2}=-{gR^2\over(y+R)^2}.\]

Mostraremos que hay un número\(v_e\), llamado la velocidad de escape, con estas propiedades:

Si\(v_0\ge v_e\) entonces\(v(t)>0\) para todos\(t>0\), y el vehículo sigue subiendo para todos\(t>0\); es decir, “escapa” de la Tierra. (¿Es realmente tan obvio que\(\lim_{t\to\infty}y(t)=\infty\) en este caso? Para una prueba, véase Ejercicio 4.3.20.)
Si\(v_0 < v_e\) entonces\(v(t)\) disminuye a cero y se vuelve negativo. Por lo tanto el vehículo alcanza una altitud máxima\(y_{m}\) y vuelve a caer a la Tierra.

Dado que la Ecuación\ ref {eq:4.3.20} es de segundo orden, no podemos resolverla por métodos discutidos hasta ahora. Sin embargo, nos preocupa\(v\) más que\(y\), y\(v\) es más fácil de encontrar. Dado que\(v=y'\) la regla de la cadena implica que

\[{d^2y\over dt^2}={dv\over dt}={dv\over dy}{dy\over dt}=v{dv\over dy}. \nonumber \]

Sustituyendo esto en la Ecuación\ ref {eq:4.3.20} produce la ecuación separable de primer orden

\[\label{eq:4.3.21} v{dv\over dy}=-{gR^2\over(y+R)^2}.\]

Cuando\(t=0\), la velocidad es\(v_0\) y la altitud es\(h\). Por lo tanto podemos obtener\(v\) en función de\(y\) resolviendo el problema de valor inicial

\[v{dv\over dy}=-{gR^2\over(y+R)^2},\quad v(h)=v_0.\nonumber\]

Ecuación integradora\ ref {eq:4.3.21} con respecto a\(y\) rendimientos

\[\label{eq:4.3.22} {v^2\over 2}={gR^2\over y+R}+c.\]

Dado que\(v(h)=v_0\),

\[c={v_0^2\over 2}-{gR^2\over h+R},\nonumber\]

así que la ecuación\ ref {eq:4.3.22} se convierte

\[\label{eq:4.3.23} {v^2\over 2}={gR^2\over y+R}+\left({v_0^2\over 2}- {gR^2\over h+R}\right).\]

\[v_0 \ge\left({2gR^2\over h+R}\right)^{1/2},\nonumber\]

la expresión entre paréntesis en la Ecuación\ ref {eq:4.3.23} no es negativa, así que\(v(y)>0\) para\(y>h\). Esto prueba que hay una velocidad de escape\(v_e\). Ahora vamos a demostrar que

\[v_e=\left({2gR^2\over h+R}\right)^{1/2}\nonumber\]

mostrando que el vehículo vuelve a caer a la Tierra si

\[\label{eq:4.3.24} v_0 <\left({2gR^2\over h+R}\right)^{1/2}.\]

Si la Ecuación\ ref {eq:4.3.24} se mantiene entonces la expresión entre paréntesis en la Ecuación\ ref {eq:4.3.23} es negativa y el vehículo alcanzará una altitud máxima\(y_m>h\) que satisfaga la ecuación

\[0={gR^2\over y_m+R}+\left({v_0^2\over 2}- {gR^2\over h+R}\right).\nonumber\]

La velocidad será cero a la altitud máxima, y el objeto caerá entonces a la Tierra bajo la influencia de la gravedad.