4.5: Aplicaciones a Curvas
- Page ID
- 114929
Comenzamos con dos ejemplos de familias de curvas generadas variando un parámetro sobre un conjunto de números reales.
Para cada valor del parámetro\(c\), la ecuación
\[\label{eq:4.5.1} y-cx^2=0\]
define una curva en el\(xy\) plano. Si\(c \ne0\), la curva es una parábola a través del origen, abriéndose hacia arriba si\(c>0\) o hacia abajo si\(c<0\). Si\(c=0\), la curva es el\(x\) eje (Figura 4.5.1 ).
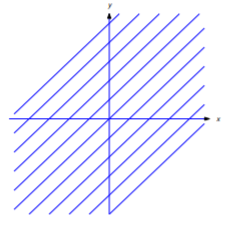
Para cada valor del parámetro\(c\) la ecuación
\[\label{eq:4.5.2} y=x+c\]
define una línea con pendiente 1 (Figura 4.5.2 ).
Una ecuación que se puede escribir en la forma
\[\label{eq:4.5.3} H(x,y,c)=0\]
se dice que define una familia de curvas de un parámetro si\(,\) por cada valor de\(c\) in en algún conjunto no vacío de números reales\(,\) el conjunto de puntos\((x,y)\) que satisfacen la ecuación\ ref {eq:4.5.3} forma una curva en el\(xy\) plano.
Ecuaciones La ecuación\ ref {eq:4.5.1} y la ecuación\ ref {eq:4.5.2} definen familias de curvas de un parámetro. (Aunque la Ecuación\ ref {eq:4.5.2} no está en la forma Ecuación\ ref {eq:4.5.3}, se puede escribir de esta forma como\(y-x-c=0\).)
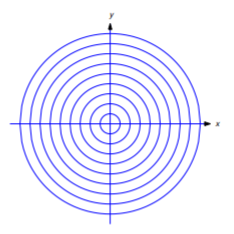
Si\(c>0\), la gráfica de la ecuación
\[\label{eq:4.5.4} x^2+y^2-c=0\]
es un círculo con centro en\((0,0)\) y radio\(\sqrt{c}\). Si\(c=0\), la gráfica es el punto único\((0,0)\). (No consideramos un solo punto como una curva.) Si\(c<0\), la ecuación no tiene gráfica. Por lo tanto, la ecuación\ ref {eq:4.5.4} define una familia de curvas de un parámetro para valores positivos de\(c\). Esta familia consta de todos los círculos centrados en\((0,0)\) (Figura 4.5.3 ).
La ecuación
\[x^2+y^2+c^2=0 \nonumber\]
no define una familia de curvas de un parámetro, ya que no\((x,y)\) satisface la ecuación si\(c\ne0\), y sólo el punto único\((0,0)\) la satisface si\(c=0\).
Recordemos de la Sección 1.2 que la gráfica de una solución de una ecuación diferencial se denomina curva integral de la ecuación. Resolver una ecuación diferencial de primer orden generalmente produce una familia de curvas integrales de un parámetro de la ecuación. Aquí nos interesa el problema inverso: dada una familia de curvas de un parámetro, existe una ecuación diferencial de primer orden para la cual cada miembro de la familia es una curva integral. Esto sugiere la siguiente definición.
4.5.2 Si cada curva en una familia de un parámetro definida por la ecuación
\[\label{eq:4.5.5} H(x,y,c)=0\]
es una curva integral de la ecuación diferencial de primer orden
\[\label{eq:4.5.6} F(x,y,y')=0,\]
entonces Ecuación\ ref {eq:4.5.6} se dice que es una ecuación diferencial para la familia.
Para encontrar una ecuación diferencial para una familia de un parámetro, diferenciamos su ecuación definitoria Ecuación\ ref {eq:4.5.5} implícitamente con respecto a\(x\), para obtener
\[\label{eq:4.5.7} H_x(x,y,c)+H_y(x,y,c)y'=0.\]
Si esta ecuación no lo hace, entonces es una ecuación diferencial para la familia. Si contiene\(c\), puede ser posible obtener una ecuación diferencial para la familia eliminando\(c\) entre la Ecuación\ ref {eq:4.5.5} y la Ecuación\ ref {eq:4.5.7}.
Encontrar una ecuación diferencial para la familia de curvas definida por
\[\label{eq:4.5.8} y=cx^2.\]
Solución
Ecuación diferenciadora\ ref {eq:4.5.8} con respecto a\(x\) rendimientos
\[y'=2cx. \nonumber\]
Por lo tanto\(c=y'/2x\), y sustituyendo esto en la Ecuación\ ref {eq:4.5.8} rinde
\[y={xy'\over2} \nonumber\]
como una ecuación diferencial para la familia de curvas definida por la ecuación\ ref {eq:4.5.8}. La gráfica de cualquier función de la forma\(y=cx^2\) es una curva integral de esta ecuación.
El siguiente ejemplo muestra que los miembros de una familia dada de curvas pueden obtenerse uniendo curvas integrales para más de una ecuación diferencial.
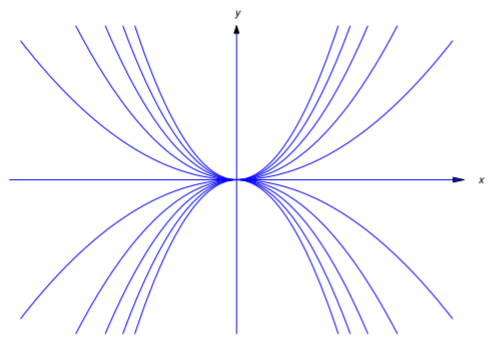
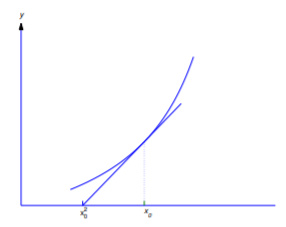
a. tratar de encontrar una ecuación diferencial para la familia de líneas tangentes a la parábola\(y=x^2\).
b. Encuentra dos líneas tangentes a la parábola\(y=x^2\) que atraviesan\((2,3)\), y encuentra los puntos de tangencia.
Solución
a. La ecuación de la línea a través de un punto dado\((x_0,y_0)\) con pendiente\(m\) es
\[\label{eq:4.5.9} y=y_0+m(x-x_0).\]
Si\((x_0,y_0)\) está en la parábola, entonces\(y_0=x_0^2\) y la pendiente de la línea tangente a través de (\(x_0,x_0^2)\)es\(m=2x_0\); por lo tanto, Ecuación\ ref {eq:4.5.9} se convierte
\[y=x_0^2+2x_0(x-x_0), \nonumber\]
o, equivalentemente,
\[\label{eq:4.5.10} y=-x_0^2+2x_0x.\]
Aquí\(x_0\) juega el papel de la constante\(c\) en Definición 4.5.1 ; es decir, variar\(x_0\) sobre\((-\infty,\infty)\) produce la familia de líneas tangentes a la parábola\(y=x^2\).
Ecuación diferenciadora\ ref {eq:4.5.10} con respecto a\(x\) los rendimientos\(y'=2x_0\).. Podemos expresar\(x_0\) en términos de\(x\) y\(y\) reescribiendo la ecuación\ ref {eq:4.5.10} como
\[x_0^2-2x_0x+y=0 \nonumber\]
y utilizando la fórmula cuadrática para obtener
\[\label{eq:4.5.11} x_0=x\pm\sqrt{x^2-y}.\]
Debemos elegir el signo más en la Ecuación\ ref {eq:4.5.11} si\(x<x_0\) y el signo menos si\(x>x_0\); así,
\[x_0=\left(x+\sqrt{x^2-y}\right)\, \text{if} \, x<x_0. \nonumber\]
y
\[x_0=\left(x-\sqrt{x^2-y}\right)\, \text{if} \, x>x_0. \nonumber\]
Ya que\(y'=2x_0\), esto implica que
\[\label{eq:4.5.12} y'=2\left(x+\sqrt{x^2-y}\right),\quad \text{if} \quad x<x_0\]
y
\[\label{eq:4.5.13} y'=2\left(x-\sqrt{x^2-y}\right),\quad \text{if} \quad x>x_0.\]
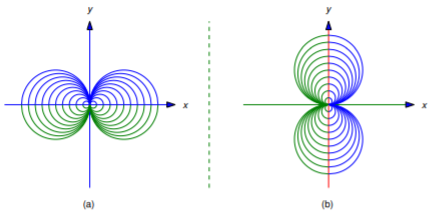
Ni la Ecuación\ ref {eq:4.5.12} ni la Ecuación\ ref {eq:4.5.13} son una ecuación diferencial para la familia de líneas tangentes a la parábola\(y=x^2\). Sin embargo, si se considera que cada línea tangente consiste en dos medias líneas tangentes unidas en el punto de tangencia, la Ecuación\ ref {eq:4.5.12} es una ecuación diferencial para la familia de medias líneas tangentes en la que\(x\) es menor que la abscisa del punto de tangencia (Figura 4.5.4 a), mientras que la Ecuación\ ref {eq:4.5.13} es una ecuación diferencial para la familia de medias líneas tangentes en la que\(x\) es mayor que esta abscisa (Figura 4.5.4 (b)). La parábola\(y=x^2\) es también una curva integral tanto de la Ecuación\ ref {eq:4.5.12} como de la Ecuación\ ref {eq:4.5.13}.
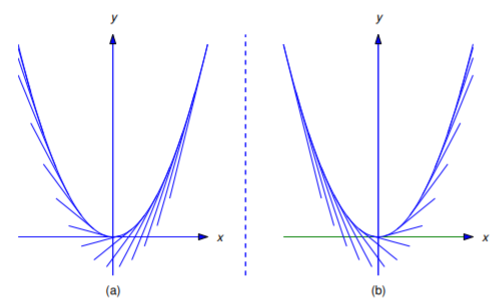
b. De la Ecuación\ ref {eq:4.5.10} el punto\((x,y)=(2,3)\) está en la línea tangente a través de\((x_0,x_0^2)\) si y solo si
\[3=-x_0^2+4x_0, \nonumber\]
que es equivalente a
\[x_0^2-4x_0+3=(x_0-3)(x_0-1)=0. \nonumber\]
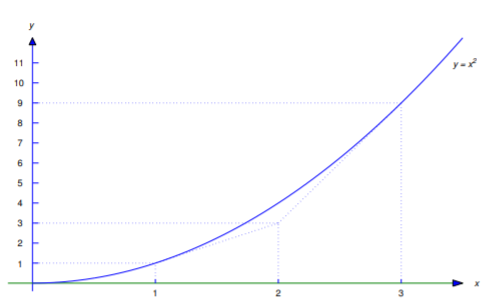
Dejar\(x_0=3\) en la ecuación\ ref {eq:4.5.10} muestra que\((2,3)\) está en la línea
\[y=-9+6x, \nonumber \]
que es tangente a la parábola en\((x_0,x_0^2)=(3,9)\), como se muestra en la Figura 4.5.5
Dejar\(x_0=1\) en la ecuación\ ref {eq:4.5.10} muestra que\((2,3)\) está en la línea
\[y=-1+2x, \nonumber\]
que es tangente a la parábola en\((x_0,x_0^2)=(1,1)\), como se muestra en la Figura 4.5.5 .
Problemas Geométricos
Consideramos ahora algunos problemas geométricos que pueden resolverse mediante ecuaciones diferenciales.
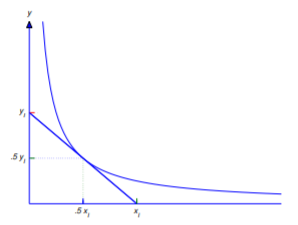
Encuentre curvas de\(y=y(x)\) tal manera que cada punto\((x_0,y(x_0))\) de la curva sea el punto medio del segmento de línea con puntos finales en los ejes de coordenadas y tangente a la curva en\((x_0,y(x_0))\) (Figura 4.5.6 ).
Solución
La ecuación de la línea tangente a la curva en\(P=(x_0,y(x_0)\) es
\[y=y(x_0)+y'(x_0)(x-x_0). \nonumber\]
Si denotamos las\(y\) intercepciones\(x\) e de la línea tangente por\(x_I\) y\(y_I\) (Figura 4.5.6 ), entonces
\[\label{eq:4.5.14} 0=y(x_0)+y'(x_0)(x_I-x_0)\]
y
\[\label{eq:4.5.15} y_I=y(x_0)-y'(x_0)x_0.\]
De la Figura 4.5.6 ,\(P\) se encuentra el punto medio del segmento de línea que conecta\((x_I,0)\) y\((0,y_I)\) si y solo si\(x_I=2x_0\) y\(y_I=2y(x_0)\). Sustituyendo la primera de estas condiciones en la Ecuación\ ref {eq:4.5.14} o la segunda en la Ecuación\ ref {eq:4.5.15} rendimientos
\[y(x_0)+y'(x_0)x_0=0. \nonumber\]
Ya que\(x_0\) es arbitrario bajamos el subíndice y concluimos que\(y=y(x)\) satisface
\[y+xy'=0, \nonumber\]
que se puede reescribir como
\[(xy)'=0. \nonumber\]
Integración de rendimientos\(xy=c\), o
\[y={c\over x}. \nonumber\]
Si\(c=0\) esta curva es la línea\(y=0\), que no satisface los requisitos geométricos impuestos por el problema; así\(c\ne0\), y las soluciones definen una familia de hipérbolas (Figura 4.5.7 ).
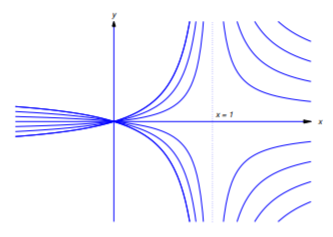
Encuentre curvas de\(y=y(x)\) tal manera que la línea tangente a la curva en cualquier punto\((x_0,y(x_0))\) intersecta el\(x\) eje en\((x^2_0,0)\). La figura 4.5.8 ilustra la situación en el caso en el que la curva está en el primer cuadrante y\(0<x<1\).
Solución
La ecuación de la línea tangente a la curva en\((x_0,y(x_0))\) es
\[y=y(x_0)+y'(x_0)(x-x_0). \nonumber\]
Dado que\((x^2_0,0)\) está en la línea tangente,
\[0=y(x_0)+y'(x_0)(x^2_0-x_0). \nonumber\]
Ya que\(x_0\) es arbitrario bajamos el subíndice y concluimos que\(y=y(x)\) satisface
\[y+y'(x^2-x)=0. \nonumber\]
Por lo tanto
\[{y'\over y}=-{1\over x^2-x}=-{1\over x(x-1)}={1\over x}-{1\over x-1},\nonumber\]
por lo
\[\ln|y|=\ln|x|-\ln|x-1|+k= \ln\left|{x\over x-1}\right|+k,\nonumber\]
y
\[y={cx\over x-1}. \nonumber\]
Si\(c=0\), la gráfica de esta función es el\(x\) eje -. Si\(c\ne0\), se trata de una hipérbola con asíntota vertical\(x=1\) y asíntota horizontal\(y=c\). En la figura 4.5.9 se muestran las gráficas para\(c\ne0\).
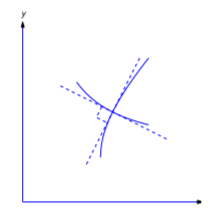
Trayectorias ortog
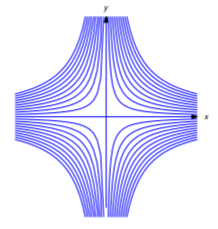
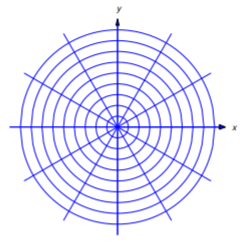
Dos curvas\(C_1\) y\(C_2\) se dice que son ortogonales en un punto de intersección\((x_0,y_0)\) si tienen tangentes perpendiculares en\((x_0,y_0)\). (Figura 4.5.10 ). Se dice que una curva es una trayectoria ortogonal de una familia dada de curvas si es ortogonal a cada curva de la familia. Por ejemplo, cada línea que atraviesa el origen es una trayectoria ortogonal de la familia de círculos centrada en el origen. Por el contrario, cualquier círculo de este tipo es una trayectoria ortogonal de la familia de líneas a través del origen (Figura 4.5.11 ).
Las trayectorias ortogonales ocurren en muchas aplicaciones físicas. Por ejemplo, si\(u=u(x,y)\) es la temperatura en un punto\((x,y)\), las curvas definidas por
\[\label{eq:4.5.16} u(x,y)=c\]
se llaman curvas isotérmicas. Las trayectorias ortogonales de esta familia se denominan líneas de flujo de calor, ya que en cualquier punto dado la dirección del flujo de calor máximo es perpendicular a la isotérmica a través del punto. Si\(u\) representa la energía potencial de un objeto que se mueve bajo una fuerza de la que depende\((x,y)\), las curvas Ecuación\ ref {eq:4.5.16} se denominan equipotenciales, y las trayectorias ortogonales se denominan líneas de fuerza.
A partir de la geometría analítica sabemos que dos líneas no verticales\(L_1\) y\(L_2\) con pendientes\(m_1\) y\(m_2\), respectivamente, son perpendiculares si y solo si\(m_2=-1/m_1\); por lo tanto, las curvas integrales de la ecuación diferencial
\[y'=-{1\over f(x,y)} \nonumber\]
son trayectorias ortogonales de las curvas integrales de la ecuación diferencial
\[y'=f(x,y), \nonumber\]
porque en cualquier punto\((x_0,y_0)\) donde las curvas de las dos familias se cruzan las pendientes de las respectivas líneas tangentes son
\[m_1=f(x_0,y_0)\quad\text{and} \quad m_2=-{1\over f(x_0,y_0)}. \nonumber\]
Esto sugiere un método para encontrar trayectorias ortogonales de una familia de curvas integrales de una ecuación de primer orden.
- Paso 1. Encontrar una ecuación diferencial\[y'=f(x,y) \nonumber \] para la familia dada.
- Paso 2. Resolver la ecuación diferencial\[y'=-{1\over f(x,y)} \nonumber \] para encontrar las trayectorias ortogonales.
Encuentra las trayectorias ortogonales de la familia de círculos
\[\label{eq:4.5.17} x^2+y^2=c^2 \quad (c>0).\]
Solución
Para encontrar una ecuación diferencial para la familia de círculos diferenciamos Ecuación\ ref {eq:4.5.17} implícitamente con respecto\(x\) a obtener
\[2x+2yy'=0, \nonumber\]
o
\[y'=-{x\over y}. \nonumber\]
Por lo tanto, las curvas integrales de
\[y'={y\over x} \nonumber\]
son trayectorias ortogonales de la familia dada. Te dejamos verificar que la solución general de esta ecuación es
\[y=kx, \nonumber\]
donde\(k\) es una constante arbitraria. Esta es la ecuación de una línea no vertical a través\((0,0)\). El\(y\) eje es también una trayectoria ortogonal de la familia dada. Por lo tanto, cada línea que atraviesa el origen es una trayectoria ortogonal de la familia dada Ecuación\ ref {eq:4.5.17} (Figura 4.5.11 ). Esto es consistente con el teorema de la geometría plana que establece que un diámetro de un círculo y una línea tangente al círculo al final del diámetro son perpendiculares.
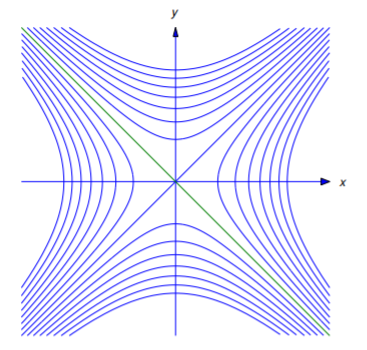
Encuentra las trayectorias ortogonales de la familia de hipérbolas
\[\label{eq:4.5.18} xy=c \quad (c\ne0)\]
(Figura 4.5.7 ).
Solución
Ecuación diferenciadora\ ref {eq:4.5.18} implícitamente con respecto a\(x\) rendimientos
\[y+xy'=0, \nonumber\]
o
\[y'=-{y\over x}; \nonumber\]
así, las curvas integrales de
\[y'={x\over y} \nonumber\]
son trayectorias ortogonales de la familia dada. Separación de rendimientos de variables
\[y'y=x \nonumber\]
e integrando rendimientos
\[y^2-x^2=k, \nonumber\]
que es la ecuación de una hipérbola if\(k \ne0\), o de las líneas\(y=x\) y\(y=-x\) if\(k=0\) (Figura 4.5.12 ).
Encuentra las trayectorias ortogonales de la familia de círculos definidos por
\[\label{eq:4.5.19} (x-c)^2+y^2=c^2 \quad (c\ne0).\]
Estos círculos están centrados en el\(x\) eje -y tangentes al\(y\) eje -eje (Figura 4.5.13 a).
Solución
Multiplicando el lado izquierdo de la ecuación\ ref {eq:4.5.19} rendimientos
\[\label{eq:4.5.20} x^2-2cx+y^2=0,\]
y diferenciando esto implícitamente con respecto a\(x\) los rendimientos
\[\label{eq:4.5.21} 2(x-c)+2yy'=0.\]
De la ecuación\ ref {eq:4.5.20},
\[c={x^2+y^2\over2x}, \nonumber \]
por lo
\[x-c=x-{x^2+y^2\over2x}={x^2-y^2\over2x}. \nonumber\]
Sustituyendo esto en la Ecuación\ ref {eq:4.5.21} y resolviendo\(y'\) rendimientos
\[\label{eq:4.5.22} y'={y^2-x^2\over2xy}.\]
Las curvas definidas por la Ecuación\ ref {eq:4.5.19} son curvas integrales de la Ecuación\ ref {eq:4.5.22}, y las curvas integrales de
\[y'={2xy\over x^2-y^2} \nonumber\]
son trayectorias ortogonales de la familia Ecuación\ ref {eq:4.5.19}. Se trata de una ecuación homogénea no lineal, la cual estudiamos en la Sección 2.4. Sustitución de\(y=ux\) rendimientos
\[u'x+u={2x(ux)\over x^2-(ux)^2}={2u\over1-u^2}, \nonumber\]
por lo
\[u'x={2u\over1-u^2}-u={u(u^2+1)\over1-u^2}, \nonumber\]
Separación de rendimientos de variables
\[{1-u^2\over u(u^2+1)}u'={1\over x}, \nonumber\]
o, equivalentemente,
\[\left[{1\over u}-{2u\over u^2+1}\right]u'={1\over x}. \nonumber\]
Por lo tanto
\[\ln |u|-\ln (u^2+1)=\ln |x|+k. \nonumber\]
Al sustituir\(u=y/x\), vemos que
\[\ln|y|-\ln|x|-\ln(x^2+y^2)+\ln(x^2)=\ln|x|+k, \nonumber\]
que, ya que\(\ln(x^2)=2\ln|x|\), equivale a
\[\ln|y|-\ln(x^2+y^2)=k, \nonumber\]
o
\[|y|=e^k(x^2+y^2). \nonumber\]
Para ver cuáles son estas curvas reescribimos esta ecuación como
\[x^2+|y|^2-e^{-k}|y|=0 \nonumber\]
y completar el cuadrado para obtener
\[x^2+(|y|-e^{-k}/2)^2=(e^{-k}/2)^2. \nonumber\]
Esto se puede reescribir como
\[x^2+(y-h)^2=h^2, \nonumber\]
donde
\[h=\left\{\begin{array}{rl} {e^{-k}\over2}&\text{ if } y\ge 0,\\[4pt]-{e^{-k}\over2}&\mbox{ if } y\le0. \end{array}\right. \nonumber\]
Así, las trayectorias ortogonales son círculos centrados en el\(y\) eje y tangentes al\(x\) eje (Figura 4.5.13 (b)). Los círculos para los cuales\(h>0\) están por encima del\(x\) eje -, mientras que aquellos para los que\(h<0\) están abajo.