4.4E: Ecuaciones Autónomas de Segundo Orden (Ejercicios)

Q4.4.1

En Ejercicios 4.4.1-4.4.4 encontramos las ecuaciones de las trayectorias de la ecuación no amortiguada dada. Identificar las soluciones de equilibrio, determinar si son estables o inestables, y trazar algunas trayectorias.

1. \(y''+y^3=0\)

2. \(y''+y^2=0\)

3. \(y''+y|y|=0\)

4. \(y''+ye^{-y}=0\)

Q4.4.2

En Ejercicios 4.4.5—4.4.8 encontramos las ecuaciones de las trayectorias de la ecuación no amortiguada dada. Identificar las soluciones de equilibrio, determinar si son estables o inestables, y encontrar las ecuaciones de las separatrices (es decir, las curvas a través de los equilibrios inestables). Trazar las separatrices y algunas trayectorias en cada una de las regiones del plano Poincaré determinadas por ellas.

5. \(y''-y^3+4y=0\)

6. \(y''+y^3-4y=0\)

7. \(y''+y(y^2-1)(y^2-4)=0\)

8. \(y''+y(y-2)(y-1)(y+2)=0\)

Q4.4.3

En los Ejercicios 4.4.9—4.4.12 trazan algunas trayectorias de la ecuación dada para diversos valores (positivo, negativo, cero) del parámetro a, encontrar los equilibrios de la ecuación y clasificarlos como estables o inestables. Explique por qué las gráficas del plano de fase correspondientes a valores positivos y negativos de a difieren tan marcadamente. ¿Se te ocurre una razón por la que cero merece ser llamado el valor crítico de\(a\)?

9. \(y''+y^2-a=0\)

10. \(y''+y^3-ay=0\)

11. \(y''-y^3+ay=0\)

12. \(y''+y-ay^3=0\)

Q4.4.4

En Ejercicios 4.4.13-4.4.18 graficar trayectorias de la ecuación dada para\(c = 0\) y pequeños valores distintos de cero (positivos y negativos) de\(c\) para observar los efectos del amortiguamiento.

13. \(y''+cy'+y^3=0\)

14. \(y''+cy'-y=0\)

15. \(y''+cy'+y^3=0\)

16. \(y''+cy'+y^2=0\)

17. \(y''+cy'+y|y|=0\)

18. \(y''+y(y-1)+cy=0\)

Q4.4.5

19. La ecuación de van der Pol

\[y''-\mu(1-y^2)y'+y=0, \tag{A}\]

donde\(\mu\) es una constante positiva y\(y\) es corriente eléctrica (Sección 6.3), surge en el estudio de un circuito eléctrico cuyas propiedades resistivas dependen de la corriente. El término de amortiguación\(-\mu(1-y^2)y'\) funciona para reducir\(|y|\) si\(|y|<1\) o para aumentar\(|y|\) si\(|y|>1\). Se puede demostrar que la ecuación de van der Pol tiene exactamente una trayectoria cerrada, que se denomina ciclo límite. Trayectorias dentro del ciclo límite espiral hacia él, mientras que las trayectorias fuera del ciclo límite espiran hacia adentro hacia él (Figura [figura:4.4.16}). Utilice su software de ecuaciones diferenciales favorito para verificar esto para\(\mu=.5,1.1.5,2\). Use una rejilla con\(-4<y<4\) y\(-4<v<4\).

Figura 4.4E.16 : Trayectorias de la euqación de van der Pol

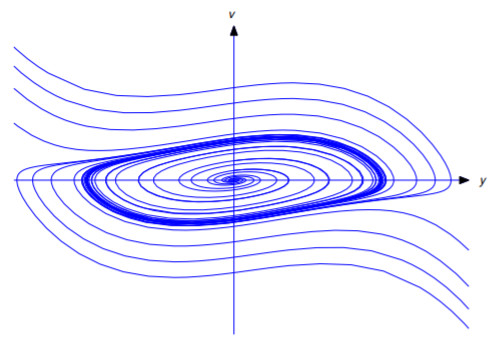
20. La ecuación de Rayleigh,

\[y''-\mu(1-(y')^2/3)y'+y=0\]

también tiene un ciclo límite. Siga las instrucciones del Ejercicio 4.4.19 para esta ecuación.

21. En relación con la Ecuación 4.4.16, supongamos\(y(0)=0\) y\(y'(0)=v_0\), dónde\(0<v_0<v_c\).

1. \(T_1\)Sea el tiempo requerido\(y\) para que aumente de cero a\(y_{\max}=2\sin^{-1}(v_0/v_c)\). Demostrar que\[{dy\over dt}=\sqrt{v_0^2-v_c^2\sin^2y/2},\quad 0\le t<T_1. \tag{A}\]
2. Separar las variables en (A) y mostrar que\[T_1=\int_0^{y_{\max}}{du\over\sqrt{v_0^2-v_c^2\sin^2u/2}} \tag{B}\]
3. Sustituir\(\sin u/2=(v_0/v_c)\sin\theta\) en (B) para obtener\[T_1=2\int_0^{\pi/2}{d\theta\over\sqrt{v_c^2-v_0^2\sin^2\theta}}. \tag{C}\]
4. Concluir desde la simetría que el tiempo requerido\((y(t),v(t))\) para recorrer la trayectoria\[v^2=v_0^2-v_c^2\sin^2y/2\] es\(T=4T_1\), y que consecuentemente\(y(t+T)=y(t)\) y\(v(t+T)=v(t)\); es decir, la oscilación es periódica con periodo\(T\).
5. Demostrar que si\(v_0=v_c\), la integral en (C) es impropia y diverge a\(\infty\). Concluir de esto que\(y(t)<\pi\) para todos\(t\) y\(\lim_{t\to\infty}y(t)=\pi\).

22. Dar una definición directa de un equilibrio inestable de\(y''+p(y)=0\).

23. Dejar\(p\) ser continuo para todos\(y\) y\(p(0)=0\). Supongamos que hay un número positivo\(\rho\) tal que\(p(y)>0\) si\(0<y\le \rho\) y\(p(y)<0\) si\(-\rho\le y<0\). Para\(0<r\le\rho\) dejar

\[\alpha(r)=\min\left\{\int_0^r p(x)\,dx,\ \int_{-r}^0 |p(x)|\,dx\right\} \mbox{\quad and \quad} \beta(r)=\max\left\{\int_0^r p(x)\,dx,\ \int_{-r}^0 |p(x)|\,dx\right\}.\]

\(y\)Sea la solución del problema de valor inicial

\[y''+p(y)=0,\quad y(0)=v_0,\quad y'(0)=v_0,\]

y definir\(c(y_0,v_0)=v_0^2+2\int_0^{y_0}p(x)\,dx\).

1. Demostrar que\[0<c(y_0,v_0) <v_0^2+2\beta(|y_0|)\mbox{\quad if \quad} 0<|y_0|\le\rho.\]
2. Demostrar que\[v^2+2\int_0^y p(x)\,dx=c(y_0,v_0),\quad t>0.\]
3. Concluir de (b) que si\(c(y_0,v_0)<2\alpha(r)\) entonces\(|y|<r,\ t>0\).
4. Dado\(\epsilon>0\),\(\delta>0\) déjese elegir para que\[\delta^2+2\beta(\delta)<\max\left\{\epsilon^2/2,2\alpha(\epsilon/\sqrt2) \right\}.\] Mostrar eso si\(\sqrt{y_0^2+v_0^2}<\delta\) entonces\(\sqrt{y^2+v^2}<\epsilon\) por\(t>0\), lo que implica que\(\overline y=0\) es un equilibrio estable de\(y''+p(y)=0\).
5. Ahora vamos a\(p\) ser continuos para todos\(y\) y\(p(\overline y)=0\), donde no\(\overline y\) es necesariamente cero. Supongamos que hay un número positivo\(\rho\) tal que\(p(y)>0\) si\(\overline y<y\le \overline y+\rho\) y\(p(y)<0\) si\(\overline y-\rho\le y<\overline y\). Demostrar que\(\overline y\) es un equilibrio estable de\(y''+p(y)=0\).

24. Que\(p\) sea continuo para todos\(y\).

1. Supongamos\(p(0)=0\) y hay un número positivo\(\rho\) tal que\(p(y)<0\) si\(0<y\le \rho\). Que\(\epsilon\) sea cualquier número tal que\(0<\epsilon<\rho\). Mostrar que si\(y\) es la solución del problema de valor inicial\[y''+p(y)=0,\quad y(0)=y_0,\quad y'(0)=0\] con\(0<y_0<\epsilon\), entonces\(y(t)\ge\epsilon\) para algunos\(t>0\). Concluir que\(\overline y=0\) es un equilibrio inestable de\(y''+p(y)=0\).
2. Ahora vamos\(p(\overline y)=0\), donde\(\overline y\) no es necesariamente cero. Supongamos que hay un número positivo\(\rho\) tal que\(p(y)<0\) si\(\overline y<y\le \overline y+\rho\). Demostrar que\(\overline y\) es un equilibrio inestable de\(y''+p(y)=0\).
3. Modifique sus pruebas de (a) y (b) para demostrar que si hay un número positivo\(\rho\) tal que\(p(y)>0\) si\(\overline y-\rho\le y<\overline y\), entonces\(\overline y\) es un equilibrio inestable de\(y''+p(y)=0\).