5.3: Ecuaciones lineales no homogéneas

Última actualización
Guardar como PDF

Page ID: 114946

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Ahora consideraremos la ecuación lineal de segundo orden no homogénea

\[\label{eq:5.3.1} y''+p(x)y'+q(x)y=f(x),\]

donde la función de forzamiento\(f\) no es idéntica a cero. El siguiente teorema, una extensión del Teorema 5.1.1, da condiciones suficientes para la existencia y singularidad de soluciones de problemas de valor inicial para la Ecuación\ ref {eq:5.3.1}. Omitimos la prueba, que está más allá del alcance de este libro.

Teorema 5.3.1 : Unicidad

Supongamos\(p,\)\(,q\) y\(f\) son continuos en un intervalo abierto\((a,b),\) deja\(x_0\) ser cualquier punto adentro\((a,b),\) y dejar\(k_0\) y\(k_1\) ser números reales arbitrarios\(.\) Entonces el problema del valor inicial

\[y''+p(x)y'+q(x)y=f(x), \quad y(x_0)=k_0,\quad y'(x_0)=k_1\nonumber \]

tiene una solución única en\((a,b).\)

Para encontrar la solución general de la Ecuación\ ref {eq:5.3.1} en un intervalo\((a,b)\) donde\(p\)\(q\), y\(f\) son continuos, es necesario encontrar la solución general de la ecuación homogénea asociada

\[\label{eq:5.3.2} y''+p(x)y'+q(x)y=0\]

encendido\((a,b)\). Llamamos a Ecuación\ ref {eq:5.3.2} la ecuación complementaria para la Ecuación\ ref {eq:5.3.1}.

El siguiente teorema muestra cómo encontrar la solución general de la Ecuación\ ref {eq:5.3.1} si conocemos una solución\(y_p\) de la Ecuación\ ref {eq:5.3.1} y un conjunto fundamental de soluciones de la Ecuación\ ref {eq:5.3.2}. Llamamos a\(y_p\) una solución particular de Ecuación\ ref {eq:5.3.1}; puede ser cualquier solución que podamos encontrar, de una manera u otra.

Teorema 5.3.2

Supongamos\(p,\)\(q,\) y\(f\) son continuos en\((a,b).\) Vamos\(y_p\) a ser una solución particular de

\[\label{eq:5.3.3} y''+p(x)y'+q(x)y=f(x)\]

sobre\((a,b)\), y dejar\(\{y_1,y_2\}\) ser un conjunto fundamental de soluciones de la ecuación complementaria

\[\label{eq:5.3.4} y''+p(x)y'+q(x)y=0\]

encendido\((a,b)\). Entonces\(y\) es una solución de\(\eqref{eq:5.3.3}\) on\((a,b)\) si y solo si

\[\label{eq:5.3.5} y=y_p+c_1y_1+c_2y_2,\]

donde\(c_1\) y\(c_2\) son constantes.

Prueba

Primero mostramos que\(y\) en la Ecuación\ ref {eq:5.3.5} hay una solución de Ecuación\ ref {eq:5.3.3} para cualquier elección de las constantes\(c_1\) y\(c_2\). Ecuación diferenciadora\ ref {eq:5.3.5} rendimientos dos veces

\[y'=y_p'+c_1y_1'+c_2y_2' \quad \text{and} \quad y''=y_p''+ c_1y_1''+c_2y_2'', \nonumber\]

por lo

\[\begin{align*} y''+p(x)y'+q(x)y&=(y_p''+c_1y_1''+c_2y_2'') +p(x)(y_p'+c_1y_1'+c_2y_2') +q(x)(y_p+c_1y_1+c_2y_2)\\ &=(y_p''+p(x)y_p'+q(x)y_p)+c_1(y_1''+p(x)y_1'+q(x)y_1) +c_2(y_2''+p(x)y_2'+q(x)y_2)\\ &= f+c_1\cdot0+c_2\cdot0=f,\end{align*}\]

ya que\(y_p\) satisface la Ecuación\ ref {eq:5.3.3}\(y_1\) y\(y_2\) satisface la Ecuación\ ref {eq:5.3.4}.

Ahora vamos a mostrar que cada solución de la Ecuación\ ref {eq:5.3.3} tiene la forma Ecuación\ ref {eq:5.3.5} para alguna elección de las constantes\(c_1\) y\(c_2\). Supongamos que\(y\) es una solución de la Ecuación\ ref {eq:5.3.3}. Mostraremos que\(y-y_p\) es una solución de la Ecuación\ ref {eq:5.3.4}, y por tanto de la forma\(y-y_p=c_1y_1+c_2y_2\), que implica Ecuación\ ref {eq:5.3.5}. Para ver esto, calculamos

\[\begin{align*} (y-y_p)''+p(x)(y-y_p)'+q(x)(y-y_p)&=(y''-y_p'')+p(x)(y'-y_p') +q(x)(y-y_p)\\ &=(y''+p(x)y'+q(x)y) -(y_p''+p(x)y_p'+q(x)y_p)\\ &=f(x)-f(x)=0,\end{align*}\]

ya\(y\) y\(y_p\) ambos satisfacen la Ecuación\ ref {eq:5.3.3}.

Decimos que la Ecuación\ ref {eq:5.3.5} es la solución general de\(\eqref{eq:5.3.3}\) on\((a,b)\).

Si\(P_0\),\(P_1\), y\(F\) son continuos y no\(P_0\) tienen ceros encendidos\((a,b)\), entonces el Teorema 5.3.2 implica que la solución general de

\[\label{eq:5.3.6} P_0(x)y''+P_1(x)y'+P_2(x)y=F(x)\]

on\((a,b)\) es\(y=y_p+c_1y_1+c_2y_2\), donde\(y_p\) es una solución particular de Ecuación\ ref {eq:5.3.6} on\((a,b)\) y\(\{y_1,y_2\}\) es un conjunto fundamental de soluciones de

\[P_0(x)y''+P_1(x)y'+P_2(x)y=0\nonumber\]

encendido\((a,b)\). Para ver esto, reescribimos la Ecuación\ ref {eq:5.3.6} como

\[y''+{P_1(x)\over P_0(x)}y'+{P_2(x)\over P_0(x)}y={F(x)\over P_0(x)}\nonumber\]

y aplicar Teorema 5.3.2 con\(p=P_1/P_0\),\(q=P_2/P_0\), y\(f=F/P_0\).

Para evitar una redacción incómoda en ejemplos y ejercicios, no especificaremos el intervalo\((a,b)\) cuando solicitemos la solución general de una ecuación lineal específica de segundo orden, o un conjunto fundamental de soluciones de una ecuación lineal homogénea de segundo orden. Acordemos que esto siempre significa que queremos la solución general (o un conjunto fundamental de soluciones, según sea el caso) en cada intervalo abierto en el que\(p\),\(q\), y\(f\) son continuas si la ecuación es de la forma Ecuación\ ref {eq:5.3.3}, o en la cual\(P_0\),\(P_1\), \(P_2\), y\(F\) son continuas y no\(P_0\) tiene ceros, si la ecuación es de la forma Ecuación\ ref {eq:5.3.6}. Te dejamos identificar estos intervalos en ejemplos y ejercicios específicos.

Para completar, señalamos que si\(P_0\),,\(P_1\)\(P_2\), y todos\(F\) son continuos en un intervalo abierto\((a,b)\), pero\(P_0\) sí tienen un cero adentro\((a,b)\), entonces la Ecuación\ ref {eq:5.3.6} puede no tener una solución general\((a,b)\) en el sentido que acaba de definir. Los ejercicios 5.1.42-5.1.44 ilustran este punto para una ecuación homogénea.

En esta sección nos limitaremos a aplicaciones del Teorema 5.3.2 donde podemos adivinar la forma de la solución particular.

Ejemplo 5.3.1

Encuentre la solución general de\[\label{eq:5.3.7} y''+y=1.\]
Resolver el problema de valor inicial\[\label{eq:5.3.8} y''+y=1, \quad y(0)=2,\quad y'(0)=7.\]

Solución

a. podemos aplicar el Teorema 5.3.2 con\((a,b)= (-\infty,\infty)\), ya que las funciones\(p\equiv0\),\(q\equiv1\), y\(f\equiv1\) en la Ecuación\ ref {eq:5.3.7} son continuas en\((-\infty,\infty)\). Por inspección vemos que\(y_p\equiv1\) es una solución particular de la Ecuación\ ref {eq:5.3.7}. Dado que\(y_1=\cos x\) y\(y_2=\sin x\) forman un conjunto fundamental de soluciones de la ecuación complementaria\(y''+y=0\), la solución general de la Ecuación\ ref {eq:5.3.7} es

\[\label{eq:5.3.9} y=1+c_1\cos x + c_2\sin x.\]

b. Imponer la condición inicial\(y(0)=2\) en la Ecuación\ ref {eq:5.3.9} rinde\(2=1+c_1\), así\(c_1=1\). Ecuación diferenciadora\ ref {eq:5.3.9} rendimientos

\[y'=-c_1\sin x+c_2\cos x.\nonumber\]

La imposición de la condición inicial\(y'(0)=7\) aquí rinde\(c_2=7\), por lo que la solución de la Ecuación\ ref {eq:5.3.8} es

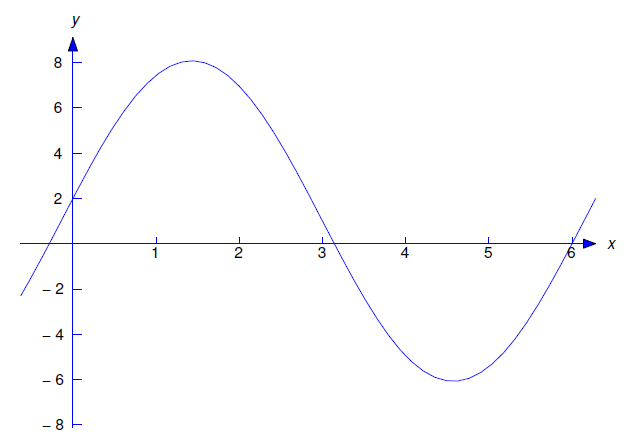
\[y=1+\cos x+7\sin x.\nonumber\]

La figura 5.3.1 es una gráfica de esta función.

Ejemplo 5.3.2

Encuentre la solución general de\[\label{eq:5.3.10} y''-2y'+y=-3-x+x^2.\]
Resolver el problema de valor inicial\[\label{eq:5.3.11} y''-2y'+y=-3-x+x^2, \quad y(0)=-2,\quad y'(0)=1.\]

Solución

a. El polinomio característico de la ecuación complementaria

\[y''-2y'+y=0 \nonumber\]

es\(r^2-2r+1=(r-1)^2\), así\(y_1=e^x\) y\(y_2=xe^x\) forman un conjunto fundamental de soluciones de la ecuación complementaria. Para adivinar una forma para una solución particular de la Ecuación\ ref {eq:5.3.10}, observamos que sustituir un polinomio de segundo grado\(y_p=A+Bx+Cx^2\) en el lado izquierdo de la Ecuación\ ref {eq:5.3.10} producirá otro polinomio de segundo grado con coeficientes que dependen de\(A\),\(B\), y\(C\). El truco es elegir\(A\),\(B\), y\(C\) así los polinomios en los dos lados de la Ecuación\ ref {eq:5.3.10} tienen los mismos coeficientes; así, si

\[y_p=A+Bx+Cx^2 \quad \text{then} \quad y_p'=B+2Cx \quad \text{and} \quad y_p''=2C, \nonumber\]

por lo

\[\begin{aligned} y_p''-2y_p'+y_p&=2C-2(B+2Cx)+(A+Bx+Cx^2)\\ &=(2C-2B+A)+(-4C+B)x+Cx^2=-3-x+x^2.\end{aligned}\nonumber \]

Equiparar coeficientes de potencias similares de\(x\) en los dos lados de los últimos rendimientos de igualdad

\[\begin{align*} C&= \phantom{-}1\phantom{.}\\ B-4C&=-1\phantom{.}\\ A-2B+2C&= -3,\end{align*}\]

entonces\(C=1\),\(B=-1+4C=3\), y\(A=-3-2C+2B=1\). Por lo tanto\(y_p=1+3x+x^2\) es una solución particular de la Ecuación\ ref {eq:5.3.10} y el Teorema 5.3.2 implica que

\[\label{eq:5.3.12} y=1+3x+x^2+e^x(c_1+c_2x) \]

es la solución general de la Ecuación\ ref {eq:5.3.10}.

b. Imponer la condición inicial\(y(0)=-2\) en la Ecuación\ ref {eq:5.3.12} rinde\(-2=1+c_1\), así\(c_1=-3\). Ecuación diferenciadora\ ref {eq:5.3.12} rendimientos

\[y'=3+2x+e^x(c_1+c_2x)+c_2e^x,\nonumber\]

e imponiendo la condición inicial\(y'(0)=1\) aquí rinde\(1=3+c_1+c_2\), entonces\(c_2=1\). Por lo tanto, la solución de la Ecuación\ ref {eq:5.3.11} es

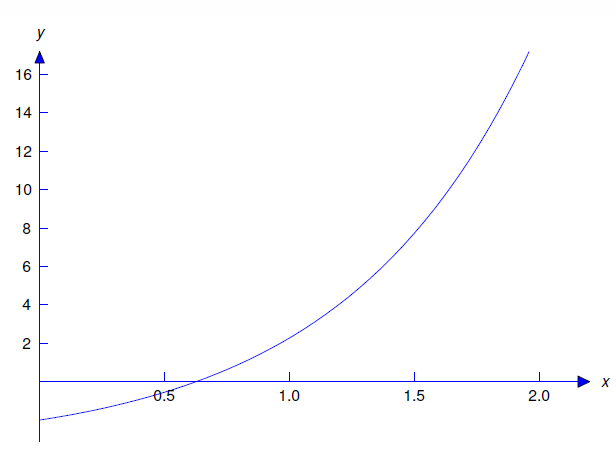
\[y=1+3x+x^2-e^x(3-x). \nonumber\]

La figura 5.3.2 es una gráfica de esta solución.

Ejemplo 5.3.3

Encuentre la solución general de

\[\label{eq:5.3.13} x^2y''+xy'-4y=2x^4\]

en\((-\infty,0)\) y\((0,\infty)\).

Solución

En el Ejemplo 5.1.3, verificamos eso\(y_1=x^2\) y\(y_2=1/x^2\) formamos un conjunto fundamental de soluciones de la ecuación complementaria

\[x^2y''+xy'-4y=0 \nonumber\]

en\((-\infty,0)\) y\((0,\infty)\). Para encontrar una solución particular de la Ecuación\ ref {eq:5.3.13}, observamos que si\(y_p=Ax^4\), donde\(A\) es una constante entonces ambos lados de la Ecuación\ ref {eq:5.3.13} serán múltiplos constantes de\(x^4\) y podemos ser capaces de elegir para\(A\) que los dos lados sean iguales. Esto es cierto en este ejemplo, ya que si\(y_p=Ax^4\) entonces

\[x^2y_p''+xy_p'-4y_p=x^2(12Ax^2)+x(4Ax^3)-4Ax^4=12Ax^4=2x^4 \nonumber\]

si\(A=1/6\); por lo tanto,\(y_p=x^4/6\) es una solución particular de la Ecuación\ ref {eq:5.3.13} on\((-\infty,\infty)\). El teorema 5.3.2 implica que la solución general de la Ecuación\ ref {eq:5.3.13} on\((-\infty,0)\) y\((0,\infty)\) es

\[y={x^4\over6}+c_1x^2+{c_2\over x^2}. \nonumber\]

El principio de superposición

El siguiente teorema nos permite romper una ecuación no homogea en partes más simples, encontrar una solución particular para cada parte y luego combinar sus soluciones para obtener una solución particular del problema original.

Teorema 5.3.3 el principio de superposición

Supongamos que\(y_{p_1}\) es una solución particular de

\[y''+p(x)y'+q(x)y=f_1(x) \nonumber\]

\((a,b)\)y\(y_{p_2}\) es una solución particular de

\[y''+p(x)y'+q(x)y=f_2(x) \nonumber\]

encendido\((a,b)\). Entonces

\[y_p=y_{p_1}+y_{p_2} \nonumber\]

es una solución particular de

\[y''+p(x)y'+q(x)y=f_1(x)+f_2(x) \nonumber\]

encendido\((a,b)\).

Prueba

Si\(y_p=y_{p_1}+y_{p_2}\) entonces

\[\begin{align*} y_p''+p(x)y_p'+q(x)y_p&=(y_{p_1}+y_{p_2})''+p(x)(y_{p_1}+y_{p_2})' +q(x)(y_{p_1}+y_{p_2})\\ &=\left(y_{p_1}''+p(x)y_{p_1}'+q(x)y_{p_1}\right) +\left(y_{p_2}''+p(x)y_{p_2}'+q(x)y_{p_2}\right)\\ &=f_1(x)+f_2(x). \end{align*}\]

Es fácil generalizar el teorema 5.3.3 a la ecuación

\[\label{eq:5.3.14} y''+p(x)y'+q(x)y=f(x)\]

donde

\[f=f_1+f_2+\cdots+f_k; \nonumber\]

por lo tanto, si\(y_{p_i}\) es una solución particular de

\[y''+p(x)y'+q(x)y=f_i(x) \nonumber\]

on\((a,b)\) for\(i=1\),\(2\),...\(k\), entonces\(y_{p_1}+y_{p_2}+\cdots+y_{p_k}\) es una solución particular de Ecuación\ ref {eq:5.3.14} on\((a,b)\). Además, mediante una prueba similar a la prueba del Teorema 5.3.3 podemos formular el principio de superposición en términos de una ecuación lineal escrita en la forma

\[P_0(x)y''+P_1(x)y'+P_2(x)y=F(x) \nonumber\]

(Ejercicio 5.3.39); es decir, si\(y_{p_1}\) es una solución particular de

\[P_0(x)y''+P_1(x)y'+P_2(x)y=F_1(x) \nonumber\]

\((a,b)\)y\(y_{p_2}\) es una solución particular de

\[P_0(x)y''+P_1(x)y'+P_2(x)y=F_2(x) \nonumber\]

en\((a,b)\), entonces\(y_{p_1}+y_{p_2}\) es una solución de

\[P_0(x)y''+P_1(x)y'+P_2(x)y=F_1(x)+F_2(x) \nonumber\]

encendido\((a,b)\).

Ejemplo 5.3.4

La función\(y_{p_1}=x^4/15\) es una solución particular de

\[\label{eq:5.3.15} x^2y''+4xy'+2y=2x^4\]

\((-\infty,\infty)\)y\(y_{p_2}=x^2/3\) es una solución particular de

\[\label{eq:5.3.16} x^2y''+4xy'+2y=4x^2\]

encendido\((-\infty,\infty)\). Utilice el principio de superposición para encontrar una solución particular de

\[\label{eq:5.3.17} x^2y''+4xy'+2y=2x^4+4x^2\]

encendido\((-\infty,\infty)\).

Solución

El lado derecho\(F(x)=2x^4+4x^2\) en la Ecuación\ ref {eq:5.3.17} es la suma de los lados derechos

\[F_1(x)=2x^4\quad \text{and} \quad F_2(x)=4x^2. \nonumber\]

en Ecuación\ ref {eq:5.3.15} y Ecuación\ ref {eq:5.3.16}. Por lo tanto, el principio de superposición implica que

\[y_p=y_{p_1}+y_{p_2}={x^4\over15}+{x^2\over3} \nonumber\]

es una solución particular de la Ecuación\ ref {eq:5.3.17}.