8.4: La función de paso de unidad
- Page ID
- 114863
En la siguiente sección consideraremos problemas de valor inicial
\[ay''+by'+cy=f(t),\quad y(0)=k_0,\quad y'(0)=k_1,\nonumber \]
donde\(a\),\(b\), y\(c\) son constantes y\(f\) es continuo por tramos. En esta sección desarrollaremos procedimientos para usar la tabla de transformaciones de Laplace para encontrar transformaciones de Laplace de funciones continuas por partes, y para encontrar las inversas continuas por partes de las transformaciones de Laplace.
Usa la tabla de transformaciones de Laplace para encontrar la transformación de Laplace de
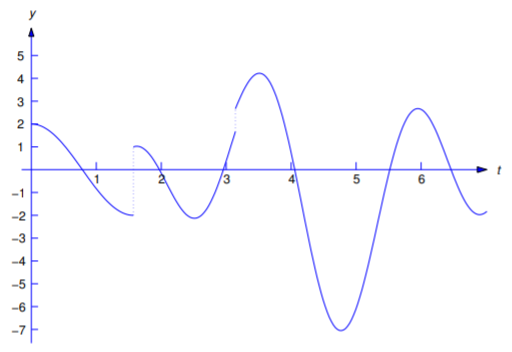
\[\label{eq:8.4.1} f(t)=\left\{\begin{array}{cl} 2t+1,&0\le t<2,\\[4pt]3t,&t\ge2 \end{array}\right.\]
(Figura 8.4.1 ).
Solución
Desde la fórmula para\(f\) los cambios en\(t=2\), escribimos
\[\label{eq:8.4.2} \begin{array}{ll} {\cal L}(f)&= \int_0^\infty e^{-st}f(t)\,dt \\{} &= \int_0^2 e^{-st}(2t+1)\,dt+\int_2^\infty e^{-st}(3t)\,dt. \end{array}\]
Para relacionar el primer término con una transformación de Laplace, sumamos y restamos
\[\int_2^\infty e^{-st}(2t+1)\,dt \nonumber\]
en Ecuación\ ref {eq:8.4.2} para obtener
\[\label{eq:8.4.3} \begin{array}{ll} {\cal L}(f) &{= \int_0^\infty e^{-st}(2t+1)\,dt+ \int_2^\infty e^{-st}(3t-2t-1)\,dt }\\ {}&= \int_0^\infty e^{-st}(2t+1)\,dt+ \int_2^\infty e^{-st}(t-1)\,dt \\{} &{={\cal L}(2t+1) + \int_2^\infty e^{-st}(t-1) \,dt.} \end{array}\]
Para relacionar la última integral con una transformación de Laplace, hacemos el cambio de variable\(x=t-2\) y reescribimos la integral como
\[\begin{aligned} \int_2^\infty e^{-st}(t-1)\,dt &= \int_0^\infty e^{-s(x+2)}(x+1)\,dx \\[4pt] &=e^{-2s}\int_0^\infty e^{-sx}(x+1)\,dx.\end{aligned}\nonumber\]
Dado que el símbolo utilizado para la variable de integración no tiene ningún efecto sobre el valor de una integral definida, ahora podemos reemplazarlo\(x\) por el más estándar\(t\) y escribir
\[\int_2^\infty e^{-st}(t-1)\,dt =e^{-2s}\int_0^\infty e^{-st}(t+1)\,dt=e^{-2s}{\cal L}(t+1).\nonumber\]
Esto y la Ecuación\ ref {eq:8.4.3} implican que
\[{\cal L}(f)={\cal L}(2t+1)+e^{-2s}{\cal L} (t+1).\nonumber\]
Ahora podemos usar la tabla de transformaciones de Laplace para encontrar que
\[{\cal L}(f)={2\over s^2}+{1\over s} +e^{-2s}\left({1\over s^2}+{1\over s}\right).\nonumber \]
Transformaciones de Laplace de funciones continuas por piezas
Ahora desarrollaremos el método de Example 8.4.1 en una forma sistemática de encontrar la transformación de Laplace de una función continua por partes. Es conveniente introducir la función de paso de unidad, definida como
\[\label{eq:8.4.4} u(t)=\left\{\begin{array}{rl} 0,&t<0\\ 1,&t\ge0. \end{array}\right.\]
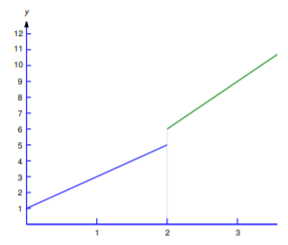
Así,\(u(t)\) “pasos” desde el valor constante\(0\) hasta el valor constante\(1\) at\(t=0\). Si reemplazamos\(t\) por\(t-\tau\) en la Ecuación\ ref {eq:8.4.4}, entonces
\[u(t-\tau)=\left\{\begin{array}{rl} 0,&t<\tau,\\ 1,&t\ge\tau \end{array}\right.; \nonumber\]
es decir, el paso ahora ocurre en\(t=\tau\) (Figura 8.4.2 ).
La función de paso nos permite representar funciones continuas por partes convenientemente. Por ejemplo, considere la función
\[\label{eq:8.4.5} f(t)=\left\{\begin{array}{rl} f_0(t),&0\le t<t_1,\\[4pt]f_1(t),&t\ge t_1, \end{array}\right.\]
donde suponemos que\(f_0\) y\(f_1\) se definan en\([0,\infty)\), a pesar de que igualan\(f\) sólo en los intervalos indicados. Esta suposición nos permite reescribir la ecuación\ ref {eq:8.4.5} como
\[\label{eq:8.4.6} f(t)=f_0(t)+u(t-t_1)\left(f_1(t)-f_0(t)\right).\]
Para verificar esto, tenga en cuenta que si\(t<t_1\) entonces\(u(t-t_1)=0\) y la ecuación\ ref {eq:8.4.6} se convierte
\[f(t)=f_0(t)+(0)\left(f_1(t)-f_0(t)\right)=f_0(t). \nonumber\]
Si\(t\ge t_1\) entonces\(u(t-t_1)=1\) y la Ecuación\ ref {eq:8.4.6} se convierte
\[f(t)=f_0(t)+(1)\left(f_1(t)-f_0(t)\right)=f_1(t). \nonumber\]
Necesitamos el siguiente teorema para mostrar cómo se puede usar la Ecuación\ ref {eq:8.4.6} para encontrar\({\cal L}(f)\).
\(g\)Sea definido en\([0,\infty).\) Supongamos\(\tau\ge0\) y\({\cal L}\left(g(t+\tau)\right)\) existe para\(s>s_0.\) Entonces\({\cal L}\left(u(t-\tau)g(t)\right)\) existe para\(s>s_0\), y
\[{\cal L}(u(t-\tau)g(t))=e^{-s\tau}{\cal L}\left(g(t+\tau)\right).\nonumber\]
- Prueba
-
Por definición,
\[{\cal L}\left(u(t-\tau)g(t)\right)=\int_0^\infty e^{-st} u(t-\tau)g(t)\, dt.\nonumber\]
A partir de esto y de la definición de\(u(t-\tau)\),
\[{\cal L}\left(u(t-\tau)g(t)\right)=\int_0^\tau e^{-st}(0)\,dt+\int_{\tau}^\infty e^{-st}g(t)\,dt.\nonumber\]
La primera integral a la derecha es igual a cero. Introduciendo la nueva variable de integración\(x=t-\tau\) en los segundos rendimientos integrales
\[{\cal L}\left(u(t-\tau)g(t)\right)=\int_0^\infty e^{-s(x+\tau)}g(x+\tau)\,dx =e^{-s\tau}\int_0^\infty e^{-sx} g(x+\tau)\,dx.\nonumber\]
Cambiar el nombre de la variable de integración en la última integral de\(x\) a\(t\) rendimientos
\[{\cal L}\left(u(t-\tau)g(t)\right) =e^{-s\tau}\int_0^\infty e^{-st} g(t+\tau)\,dt=e^{-s\tau}{\cal L}(g(t+\tau)).\nonumber\]
Encuentra\[{\cal L}\left(u(t-1)(t^2+1)\right).\nonumber\]
Solución
Aquí\(\tau=1\) y\(g(t)=t^2+1\), entonces
\[g(t+1)=(t+1)^2+1=t^2+2t+2.\nonumber\]
Desde
\[{\cal L}\left(g(t+1)\right)={2\over s^3}+{2\over s^2}+{2\over s},\nonumber\]
El teorema 8.4.1 implica que
\[{\cal L}\left(u(t-1)(t^2+1)\right) =e^{-s}\left({2\over s^3}+{2\over s^2}+{2\over s}\right).\nonumber\]
Utilice el teorema 8.4.1 para encontrar la transformación de Laplace de la función
\[f(t)=\left\{\begin{array}{cl} 2t+1,&0\le t<2,\\[4pt]3t,&t\ge2, \end{array}\right. \nonumber\]
de Ejemplo 8.4.1 .
Solución
Primero escribimos\(f\) en la forma Ecuación\ ref {eq:8.4.6} como
\[f(t)=2t+1+u(t-2)(t-1). \nonumber\]
Por lo tanto
\[\begin{aligned} {\cal L}(f)&={\cal L}(2t+1) +{\cal L}\left(u(t-2)(t-1)\right)\\ &={\cal L}(2t+1) +e^{-2s}{\cal L}(t+1)\quad\mbox{ (from Theorem }\PageIndex{1})\\ &={2\over s^2}+{1\over s}+e^{-2s}\left({1\over s^2}+{1\over s}\right),\end{aligned}\nonumber\]
que es el resultado obtenido en Ejemplo 8.4.1 .
La ecuación de fórmula\ ref {eq:8.4.6} se puede extender a funciones continuas por partes más generales. Por ejemplo, podemos escribir
\[f(t)=\left\{\begin{array}{rl} f_0(t),&0\le t<t_1,\\[4pt]f_1(t),&t_1\le t<t_2,\\[4pt]f_2(t),&t\ge t_2, \end{array}\right.\nonumber\]
como
\[f(t)=f_0(t)+u(t-t_1)\left(f_1(t)-f_0(t)\right)+ u(t-t_2)\left(f_2(t)-f_1(t)\right) \nonumber\]
si\(f_0\),\(f_1\), y\(f_2\) están todos definidos en\([0,\infty)\).
Encuentra la transformación de Laplace de
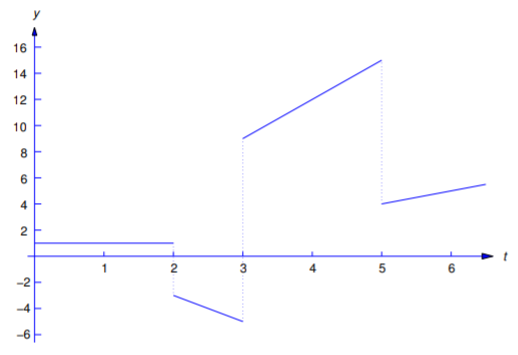
\[\label{eq:8.4.7} f(t)=\left\{\begin{array}{cl} 1,&0\le t<2,\\[4pt]-2t+1,&2\le t<3,\\[4pt]3t,&3\le t<5,\\[4pt]t-1,&t\ge5 \end{array}\right.\]
(Figura 8.4.3 ).
Solución
En términos de funciones escalonadas,
\[\begin{aligned} f(t)&=1+u(t-2)(-2t+1-1)+u(t-3)(3t+2t-1)\\ &= +u(t-5)(t-1-3t),\end{aligned}\nonumber\]
o
\[f(t)=1-2u(t-2)t+u(t-3)(5t-1)-u(t-5)(2t+1). \nonumber\]
Ahora el teorema 8.4.1 implica que
\[\begin{aligned} {\cal L}(f)&={\cal L}(1)-2e^{-2s}{\cal L}(t+2)+e^{-3s}{\cal L}\left(5(t+3)-1\right)-e^{-5s}{\cal L}\left(2(t+5)+1\right)\\[4pt]&={\cal L}(1)-2e^{-2s}{\cal L}(t+2)+e^{-3s}{\cal L}(5t+14)-e^{-5s}{\cal L}(2t+11)\\[4pt]&={1\over s}-2e^{-2s}\left({1\over s^2}+{2\over s}\right)+ e^{-3s}\left({5\over s^2}+{14\over s}\right)-e^{-5s}\left({2\over s^2}+{11\over s}\right). \end{aligned}\nonumber\]
Las identidades trigonométricas
\[\label{eq:8.4.8} \sin (A+B)=\sin A\cos B+\cos A\sin B\]
\[\label{eq:8.4.9} \cos (A+B)=\cos A\cos B-\sin A\sin B\]
son útiles en problemas que implican cambiar los argumentos de las funciones trigonométricas. Utilizaremos estas identidades en el siguiente ejemplo.
Encuentra la transformación de Laplace de
\[\label{eq:8.4.10} f(t)=\left\{\begin{array}{cl}{\sin t,}&{0\leq t<\frac{\pi }{2}}\\{\cos t-3\sin t,}&{\frac{\pi }{2}\leq t<\pi }\\{3\cos t,}&{t\geq \pi} \end{array} \right.\]
(Figura 8.4.4 ).
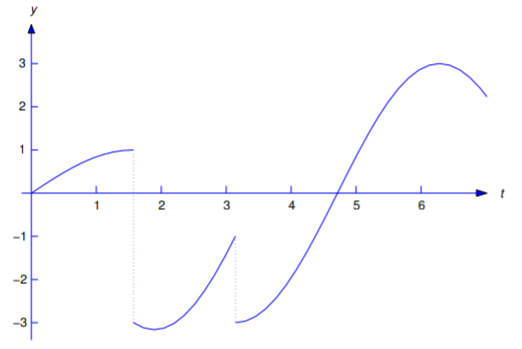
Solución
En términos de funciones escalonadas,
\[f(t)=\sin t+u(t-\pi/2) (\cos t-4\sin t)+u(t-\pi) (2 \cos t+3\sin t). \nonumber\]
Ahora el teorema 8.4.1 implica que
\[\label{eq:8.4.11} \begin{array}{ccl} {\cal L}(f)&=&{\cal L}(\sin t)+e^{-{\pi\over 2}s}{\cal L} \left(\cos\left(t+{\pi\over2}\right)-4\sin\left(t+{\pi\over2}\right)\right) \\[4pt]&&\qquad+e^{-\pi s}{\cal L}\left(2\cos(t+\pi)+3\sin(t+\pi)\right). \end{array}\]
Desde
\[\cos\left(t+{\pi\over 2}\right)-4\sin\left(t+{\pi\over 2}\right)=-\sin t-4\cos t \nonumber\]
y
\[2\cos (t+\pi)+3\sin (t+\pi)=-2\cos t-3\sin t, \nonumber\]
vemos de la Ecuación\ ref {eq:8.4.11} que
\[\begin{align*} {\cal L}(f)&={\cal L}(\sin t)-e^{-\pi s/2}{\cal L}(\sin t+4\cos t) -e^{-\pi s}{\cal L}(2\cos t+3\sin t)\\[4pt]&={1\over s^2+1}-e^{-{\pi\over 2}s}\left({1+4s\over s^2+1}\right) -e^{-\pi s}\left({3+2s\over s^2+1}\right). \end{align*}\nonumber\]
El segundo teorema del cambio
Sustituir\(g(t)\) por\(g(t-\tau)\) en Teorema 8.4.1 produce el siguiente teorema.
Si\(\tau\ge0\) y\({\cal L}(g)\) existe para\(s>s_0\) entonces\({\cal L}\left(u(t-\tau)g(t-\tau)\right)\) existe para\(s>s_0\) y
\[{\cal L}(u(t-\tau)g(t-\tau))=e^{-s\tau}{\cal L}(g(t)),\nonumber\]
o, equivalentemente,
\[\label{eq:8.4.12} \mbox{if } g(t)\leftrightarrow G(s),\mbox{ then }u(t-\tau)g(t-\tau)\leftrightarrow e^{-s\tau}G(s).\]
Recordemos que el Primer Teorema Cambiante (Teorema 8.1.3 establece que multiplicar una función por\(e^{at}\) corresponde a desplazar el argumento de su transformación por una unidades. El teorema 8.4.2 establece que multiplicar una transformada de Laplace por la exponencial\(e^{−\tau s}\) corresponde a desplazar el argumento de la transformada inversa por\(\tau \) unidades.
Usa la ecuación\ ref {eq:8.4.12} para encontrar
\[{\cal L}^{-1}\left(e^{-2s}\over s^2\right). \nonumber\]
Solución
Para aplicar la Ecuación\ ref {eq:8.4.12} dejamos\(\tau=2\) y\(G(s)=1/s^2\). Entonces\(g(t)=t\) y Ecuación\ ref {eq:8.4.12} implica que
\[{\cal L}^{-1}\left(e^{-2s}\over s^2\right)=u(t-2)(t-2).\nonumber\]
Encuentra la transformada inversa de Laplace\(h\) de
\[H(s)={1\over s^2}-e^{-s}\left({1\over s^2}+{2\over s}\right)+ e^{-4s}\left({4\over s^3}+{1\over s}\right),\nonumber\]
y encontrar fórmulas distintas para\(h\) intervalos apropiados.
Solución
Let
\[G_0(s)={1\over s^2},\quad G_1(s)={1\over s^2}+{2\over s},\quad G_2(s)={4\over s^3}+{1\over s}.\nonumber\]
Entonces
\[g_0(t)=t,\; g_1(t)=t+2,\; g_2(t)=2t^2+1.\nonumber\]
Por lo tanto, la Ecuación\ ref {eq:8.4.12} y la linealidad de\({\cal L}^{-1}\) implican que
\[\begin{aligned} h(t)&={\cal L}^{-1}\left(G_0(s)\right)-{\cal L}^{-1}\left(e^{-s}G_1(s)\right)+{\cal L}^{-1}\left(e^{-4s}G_2(s)\right)\\[4pt]&=t-u(t-1)\left[(t-1)+2\right]+u(t-4)\left[2(t-4)^2+1\right]\\[4pt]&=t-u(t-1)(t+1)+u(t-4)(2t^2-16t+33),\end{aligned}\nonumber\]
que también se puede escribir como
\[h(t)=\left\{\begin{array}{cl} t,&0\le t<1,\\[4pt]-1,&1\le t<4,\\[4pt]2t^2-16t+32,&t\ge4. \end{array}\right.\nonumber \]
Encuentra la transformación inversa de
\[H(s)={2s\over s^2+4}-e^{-{\pi\over 2}s} {3s+1\over s^2+9}+e^{-\pi s}{s+1\over s^2+6s+10}. \nonumber\]
Solución
Let
\[G_0(s)={2s\over s^2+4},\quad G_1(s)=-{(3s+1)\over s^2+9},\nonumber\]
y
\[G_2(s)={s+1\over s^2+6s+10}={(s+3)-2\over (s+3)^2+1}.\nonumber\]
Entonces
\[g_0(t)=2\cos 2t,\quad g_1(t)=-3\cos 3t-{1\over 3}\sin 3t,\nonumber\]
y
\[g_2(t)=e^{-3t}(\cos t-2\sin t).\nonumber\]
Por lo tanto, la ecuación\ ref {eq:8.4.12} y la linealidad de\({\cal L}^{-1}\) implican que
\[\begin{aligned} h(t)&=2\cos 2t-u(t-\pi/2)\left[3\cos 3(t-\pi/2)+{1\over 3}\sin 3\left(t-{\pi\over 2}\right)\right]\\[4pt] &= +u(t-\pi)e^{-3(t-\pi)}\left[\cos (t-\pi)-2\sin (t-\pi)\right].\end{aligned}\nonumber\]
Usando las identidades trigonométricas Ecuación\ ref {eq:8.4.8} y Ecuación\ ref {eq:8.4.9}, podemos reescribir esto como
\[\label{eq:8.4.13} \begin{align} h(t)&=2\cos 2t+u(t-\pi/2)\left(3\sin 3t- {1\over 3}\cos 3t\right) \\[4pt] &= -u(t-\pi)e^{-3(t-\pi)} (\cos t-2\sin t) \end{align}\]
(Figura 8.4.5 ).