9.2: Ecuaciones homogéneas de coeficiente constante de orden superior
- Page ID
- 114583
Si\(a_0\),\(a_1\),...,\(a_n\) son constantes y\(a_0\ne0\), entonces
\[a_0y^{(n)}+a_1y^{(n-1)}+\cdots+a_ny=F(x)\nonumber \]
se dice que es una ecuación de coeficiente constante. En esta sección consideramos la ecuación del coeficiente constante homogéneo
\[\label{eq:9.2.1} a_0y^{(n)}+a_1y^{(n-1)}+\cdots+a_ny=0.\]
Dado que la Ecuación\ ref {eq:9.2.1} es normal on\((-\infty,\infty)\), los teoremas de la Sección 9.1 se aplican todos con\((a,b)=(-\infty,\infty)\).
Al igual que en la Sección 5.2, llamamos
\[\label{eq:9.2.2} p(r)=a_0r^n+a_1r^{n-1}+\cdots+a_n\]
el polinomio característico de la Ecuación\ ref {eq:9.2.1}. Vimos en la Sección 5.2 que cuando\(n=2\) las soluciones de la Ecuación\ ref {eq:9.2.1} están determinadas por los ceros del polinomio característico. Esto también es cierto cuando\(n>2\), pero la situación es más complicada en este caso. En consecuencia, tomamos un enfoque diferente.
Si\(k\) es un entero positivo,\(D^k\) supongamos el\(k\) -ésimo operador derivado; es decir
\[D^ky=y^{(k)}. \nonumber\]
Si
\[q(r)=b_0r^m+b_1r^{m-1}+\cdots+b_m \nonumber\]
es un polinomio arbitrario, define el operador
\[q(D)=b_0D^m+b_1D^{m-1}+\cdots+b_m \nonumber\]
de tal manera que
\[q(D)y=(b_0D^m+b_1D^{m-1}+\cdots+b_m)y=b_0y^{(m)}+b_1y^{(m-1)}+\cdots+ b_my \nonumber\]
siempre que\(y\) sea una función con\(m\) derivados. Llamamos a\(q(D)\) un operador polinomio.
Con\(p\) como en la Ecuación\ ref {eq:9.2.2},
\[p(D)=a_0D^n+a_1D^{n-1}+\cdots+a_n, \nonumber\]
así Ecuación\ ref {eq:9.2.1} se puede escribir como\(p(D)y=0\). Si\(r\) es una constante entonces
\[\begin{align*} p(D)e^{rx}&= \left(a_0D^ne^{rx}+a_1D^{n-1}e^{rx}+\cdots+a_ne^{rx}\right)\\[4pt] &= (a_0r^n+a_1r^{n-1}+\cdots+a_n)e^{rx};\end{align*}\nonumber \]
es decir
\[p(D)(e^{rx})=p(r)e^{rx}. \nonumber\]
Esto demuestra que\(y=e^{rx}\) es una solución de la Ecuación\ ref {eq:9.2.1} si\(p(r)=0\). En el caso más simple, donde\(p\) tiene ceros reales\(n\) distintos\(r_1\),\(r_2\),...,\(r_n\), este argumento arroja\(n\) soluciones
\[y_1=e^{r_1x},\quad y_2=e^{r_2x},\dots,\quad y_n=e^{r_nx}. \nonumber\]
Se puede demostrar (Ejercicio 9.2.39) que el Wronskian de\(\{e^{r_1x},e^{r_2x},\dots,e^{r_nx}\}\) es distinto de cero si\(r_1\),\(r_2\),...,\(r_n\) son distintos; de ahí,\(\{e^{r_1x},e^{r_2x},\dots,e^{r_nx}\}\) es un conjunto fundamental de soluciones de\(p(D)y=0\) en este caso.
- Encuentre la solución general de\[\label{eq:9.2.3} y'''-6y''+11y'-6y=0.\]
- y resolver el problema de valor inicial\[\label{eq:9.2.4} y'''-6y''+11y'-6y=0, \quad y(0)=4,\quad y'(0)=5,\quad y''(0)=9.\]
Solución a
El polinomio característico de la Ecuación\ ref {eq:9.2.3} es
\[p(r)=r^3-6r^2+11r-6=(r-1)(r-2)(r-3). \nonumber\]
Por lo tanto\(\{e^x,e^{2x},e^{3x}\}\) es un conjunto de soluciones de Ecuación\ ref {eq:9.2.3}. Es un conjunto fundamental, ya que su Wronskian es
\[W(x)=\left|\begin{array}{rrr}e^x&e^{2x}&e^{3x}\\e^x&2e^{2x}& 3e^{3x}\\e^x&4e^{2x}&9e^{3x}\end{array}\right|= e^{6x}\left|\begin{array}{rrr}1&1&1\\1&2& 3\\1&4&9\end{array}\right|=2e^{6x}\ne0. \nonumber\]
Por lo tanto, la solución general de la Ecuación\ ref {eq:9.2.3} es
\[\label{eq:9.2.5} y=c_1e^{x}+c_2e^{2x}+c_3e^{3x}.\]
Solución b
Debemos determinar\(c_1\),\(c_2\) y\(c_3\) en la Ecuación\ ref {eq:9.2.5} para que\(y\) satisfaga las condiciones iniciales en la Ecuación\ ref {eq:9.2.4}. Ecuación diferenciadora\ ref {eq:9.2.5} rendimientos dos veces
\[\label{eq:9.2.6} \begin{array}{rcl} y'&=&c_1e^{x}+2c_2e^{2x}+3c_3e^{3x}\\ y''&=&c_1e^{x}+4c_2e^{2x}+9c_3e^{3x}. \end{array}\]
Ajuste\(x=0\) en Ecuación\ ref {eq:9.2.5} y Ecuación\ ref {eq:9.2.6} e imponer las condiciones iniciales rendimientos
\[\begin{array}{rcl} c_1+\phantom{2}c_2+\phantom{3}c_3&=&4\\ c_1+2c_2+3c_3&=&5\\ c_1+4c_2+9c_3&=&9. \end{array}\nonumber \]
La solución de este sistema es\(c_1=4\),\(c_2=-1\),\(c_3=1\). Por lo tanto, la solución de la Ecuación\ ref {eq:9.2.4} es
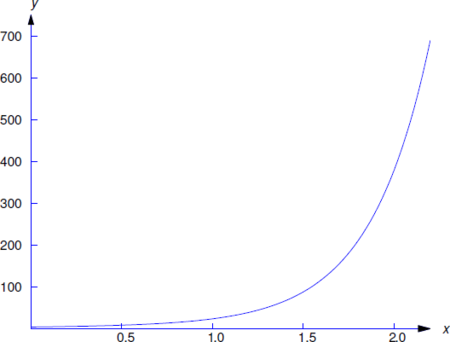
\[y=4e^x-e^{2x}+e^{3x} \nonumber\]
(Figura 9.2.1 ).
Ahora consideramos el caso donde la ecuación polinómica característica\ ref {eq:9.2.2} no tiene ceros reales\(n\) distintos. Para ello es útil definir a qué nos referimos con factorización de un operador polinómico. Comenzamos con un ejemplo.
Considerar el polinomio
\[p(r)=r^3-r^2+r-1 \nonumber\]
y el operador polinomio asociado
\[p(D)=D^3-D^2+D-1. \nonumber\]
Dado que se\(p(r)\) puede factorizar como
\[p(r)=(r-1)(r^2+1)=(r^2+1)(r-1), \nonumber\]
es razonable esperar que p (D) pueda ser factorizado como
\[\label{eq:9.2.7} p(D)=(D-1)(D^2+1)=(D^2+1)(D-1).\]
No obstante, antes de que podamos hacer esta afirmación debemos definir a qué nos referimos diciendo que dos operadores son iguales, y a qué nos referimos con los productos de los operadores en la Ecuación\ ref {eq:9.2.7}. Decimos que dos operadores son iguales si aplican a las mismas funciones y siempre producen el mismo resultado. Las definiciones de los productos en la Ecuación\ ref {eq:9.2.7} es esta: si\(y\) es alguna función tres veces diferenciable entonces
- \((D-1)(D^2+1)y\)es la función obtenida aplicando\(D^2+1\) primero\(y\) y luego aplicando\(D-1\) a la función resultante
- \((D^2+1)(D-1)y\)es la función obtenida aplicando\(D-1\) primero\(y\) y luego aplicando\(D^2+1\) a la función resultante.
De (a),
\[\label{eq:9.2.8} \begin{array}{rcl} (D-1)(D^2+1)y&=&(D-1)[(D^2+1)y]\\ &=&(D-1)(y''+y)=D(y''+y)-(y''+y)\\&=&(y'''+y')-(y''+y)\\ &=&y'''-y''+y'-y=(D^3-D^2+D-1)y. \end{array}\]
Esto implica que
\[(D-1)(D^2+1)=(D^3-D^2+D-1). \nonumber\]
De (b),
\[\label{eq:9.2.9} \begin{array}{rcl} (D^2+1)(D-1)y&=&(D^2+1)[(D-1)y]\\ &=&(D^2+1)(y'-y)=D^2(y'-y)+(y'-y)\\&=&(y'''-y'')+(y'-y)\\ &=&y'''-y''+y'-y=(D^3-D^2+D-1)y, \end{array}\]
\[(D^2+1)(D-1)=(D^3-D^2+D-1), \nonumber\]
que completa la justificación de la Ecuación\ ref {eq:9.2.7}.
Usa el resultado de Example 9.2.2 para encontrar la solución general de
\[\label{eq:9.2.10} y'''-y''+y'-y=0.\]
Solución
De la ecuación\ ref {eq:9.2.8}, podemos reescribir la ecuación\ ref {eq:9.2.10} como
\[(D-1)(D^2+1)y=0, \nonumber\]
lo que implica que cualquier solución de\((D^2+1)y=0\) es una solución de Ecuación\ ref {eq:9.2.10}. Por lo tanto\(y_1=\cos x\) y\(y_2=\sin x\) son soluciones de Ecuación\ ref {eq:9.2.10}.
De la ecuación\ ref {eq:9.2.9}, podemos reescribir la ecuación\ ref {eq:9.2.10} como
\[(D^2+1)(D-1)y=0, \nonumber\]
lo que implica que cualquier solución de\((D-1)y=0\) es una solución de Ecuación\ ref {eq:9.2.10}. Por lo tanto\(y_3=e^x\) es solución de la Ecuación\ ref {eq:9.2.10}.
El Wronskian de\(\{e^x,\cos x,\sin x\}\) es
\[W(x)=\left|\begin{array}{rrr}\cos x&\sin x&e^x\\-\sin x&\cos x&e^x\\ -\cos x&-\sin x&e^x\end{array}\right|. \nonumber\]
Desde
\[W(0)=\left|\begin{array}{rrr}1&0&1\\0&1&1\\ -1&0&1\end{array}\right|=2, \nonumber\]
\(\{\cos x,\sin x,e^x\}\)es linealmente independiente y
\[y=c_1\cos x+c_2\sin x+c_3e^x \nonumber\]
es la solución general de la Ecuación\ ref {eq:9.2.10}.
Encuentre la solución general de
\[\label{eq:9.2.11} y^{(4)}-16y=0.\]
Solución
El polinomio característico de la Ecuación\ ref {eq:9.2.11} es
\[\begin{align*} p(r) &=r^4-16 \\[4pt] &=(r^2-4)(r^2+4) \\[4pt] &=(r-2)(r+2)(r^2+4). \end{align*}\nonumber \]
Por argumentos similares a los utilizados en los Ejemplos 9.2.2 y 9.2.4 , se puede demostrar que la Ecuación\ ref {eq:9.2.11} puede escribirse como
\[(D^2+4)(D+2)(D-2)y=0 \nonumber\]
o
\[(D^2+4)(D-2)(D+2)y=0 \nonumber\]
o
\[(D-2)(D+2)(D^2+4)y=0. \nonumber\]
Por lo tanto\(y\) es una solución de la Ecuación\ ref {eq:9.2.11} si es una solución de alguna de las tres ecuaciones
\[(D-2)y=0,\quad (D+2)y=0, \quad(D^2+4)y=0. \nonumber\]
De ahí,\(\{e^{2x},e^{-2x},\cos2x,\sin2x\}\) es un conjunto de soluciones de Ecuación\ ref {eq:9.2.11}. El Wronskian de este conjunto es
\[W(x)=\left|\begin{array}{rrrr} e^{2x}&e^{-2x}&\cos2x&\sin2x\\ 2e^{2x}&-2e^{-2x}&-2\sin2x&2\cos2x\\ 4e^{2x}&4e^{-2x}&-4\cos2x&-4\sin2x\\ 8e^{2x}&-8e^{-2x}&8\sin2x&-8\cos2x\\ \end{array}\right|. \nonumber\]
Desde
\[W(0)=\left|\begin{array}{rrrr} 1&1&1&0\\ 2&-2&0&2\\ 4&4&-4&0\\ 8&-8&0&-8\\ \end{array}\right|=-512, \nonumber\]
\(\{e^{2x},e^{-2x},\cos2x,\sin2x\}\)es linealmente independiente, y
\[y_1=c_1e^{2x}+c_2e^{-2x}+c_3\cos2x+c_4\sin2x \nonumber\]
es la solución general de la Ecuación\ ref {eq:9.2.11}.
Se sabe a partir del álgebra que cada polinomio
\[p(r)=a_0r^n+a_1r^{n-1}+\cdots+a_n \nonumber\]
con coeficientes reales se pueden factorizar como
\[p(r)=a_0p_1(r)p_2(r)\cdots p_k(r), \nonumber\]
donde ningún par de los polinomios\(p_1\),\(p_2\),...,\(p_k\) tiene un factor commom y cada uno es cualquiera de la forma
\[\label{eq:9.2.12} p_j(r)=(r-r_j)^{m_j},\]
donde\(r_j\) es real y\(m_j\) es un entero positivo, o
\[\label{eq:9.2.13} p_j(r)=\left[(r-\lambda_j)^2+\omega_j^2\right]^{m_j},\]
donde\(\lambda_j\) y\(\omega_j\) son reales,\(\omega_j\ne0\), y\(m_j\) es un entero positivo. Si Ecuación\ ref {eq:9.2.12} se mantiene entonces\(r_j\) es un cero real de\(p\), mientras que si Ecuación\ ref {eq:9.2.13} se mantiene entonces\(\lambda+i\omega\) y\(\lambda-i\omega\) son ceros conjugados complejos de\(p\). En cualquier caso,\(m_j\) es la multiplicidad de los cero (s).
Por argumentos similares a los utilizados en nuestros ejemplos, se puede demostrar que
\[\label{eq:9.2.14} p(D)=a_0p_1(D)p_2(D)\cdots p_k(D)\]
y que el orden de los factores sobre la derecha pueda elegirse arbitrariamente. Por lo tanto, si\(p_j(D)y=0\) para algunos\(j\) entonces\(p(D)y=0\). Para ver esto, simplemente reescribimos la Ecuación\ ref {eq:9.2.14} para que\(p_j(D)\) se aplique primero. Por lo tanto el problema de encontrar soluciones de\(p(D)y=0\) con\(p\) como en la Ecuación\ ref {eq:9.2.14} se reduce a encontrar soluciones de cada una de estas ecuaciones
\[p_j(D)y=0,\quad 1\le j\le k, \nonumber\]
donde\(p_j\) es una potencia de un término de primer grado o de una cuadrática irreducible. Para encontrar un conjunto fundamental de soluciones\(\{y_1,y_2,\dots,y_n\}\) de\(p(D)y=0\), encontramos conjunto fundamental de soluciones de cada una de las ecuaciones y tomamos\(\{y_1,y_2,\dots,y_n\}\) como conjunto de todas las funciones en estos conjuntos fundamentales separados. En el Ejercicio 9.2.40 esbozamos la prueba que\(\{y_1,y_2,\dots,y_n\}\) es linealmente independiente, y por tanto un conjunto fundamental de soluciones de\(p(D)y=0\).
Para aplicar este procedimiento a ecuaciones de coeficientes constantes homogéneos generales, debemos ser capaces de encontrar conjuntos fundamentales de soluciones de ecuaciones de la forma
\[(D-a)^my=0 \nonumber\]
y
\[\left[(D-\lambda)^2+\omega^2\right]^my=0, \nonumber\]
donde\(m\) es un entero positivo arbitrario. Los dos teoremas siguientes muestran cómo hacer esto.
Si\(m\) es un entero positivo, entonces
\[\label{eq:9.2.15} \{e^{ax}, xe^{ax},\dots, x^{m-1}e^{ax}\}\]
es un conjunto fundamental de soluciones de
\[\label{eq:9.2.16} (D-a)^my=0.\]
- Prueba
-
Vamos a mostrar que si
\[f(x)=c_1+c_2x+\cdots+c_mx^{m-1} \nonumber\]
es un polinomio arbitrario de grado\(\le m-1\), entonces\(y=e^{ax}f\) es una solución de la Ecuación\ ref {eq:9.2.16}. Primero tenga en cuenta que si\(g\) hay alguna función diferenciable entonces
\[(D-a)e^{ax}g=De^{ax}g-ae^{ax}g=ae^{ax}g+e^{ax}g'-ae^{ax}g, \nonumber\]
por lo
\[\label{eq:9.2.17} (D-a)e^{ax}g=e^{ax}g'.\]
Por lo tanto
\[ \begin{array}{lcll} (D-a)e^{ax}f&=&e^{ax}f'&\mbox{(from \eqref{eq:9.2.17} with $g=f$)}\\ (D-a)^2e^{ax}f&=& (D-a)e^{ax}f'=e^{ax}f'' &\mbox{(from \eqref{eq:9.2.17} with $g=f'$)}\\ (D-a)^3e^{ax}f&=& (D-a)e^{ax}f''=e^{ax}f''' &\mbox{(from \eqref{eq:9.2.17} with $g=f''$)}\\ &\vdots&\\ (D-a)^me^{ax}f &=&(D-a)e^{ax}f^{(m-1)}=e^{ax}f^{(m)} &\mbox{(from \eqref{eq:9.2.17} with $g=f^{(m-1)}$)}. \end{array}\nonumber \]
Ya que\(f^{(m)}=0\), la última ecuación implica que\(y=e^{ax}f\) es una solución de la Ecuación\ ref {eq:9.2.16} si\(f\) es algún polinomio de grado\(\le m-1\). En particular, cada función en la Ecuación\ ref {eq:9.2.15} es una solución de la Ecuación\ ref {eq:9.2.16}. Para ver que la Ecuación\ ref {eq:9.2.15} es linealmente independiente (y por tanto un conjunto fundamental de soluciones de la Ecuación\ ref {eq:9.2.16}), tenga en cuenta que si
\[c_1e^{ax}+c_2xe^{ax}+c\dots+c_{m-1}x^{m-1}e^{ax}=0 \nonumber\]
para todos\(x\) en algún intervalo\((a,b)\), entonces
\[c_1+c_2x+c\dots+c_{m-1}x^{m-1}=0 \nonumber\]
para todos\(x\) en\((a,b)\). No obstante, sabemos por álgebra que si este polinomio tiene más de\(m-1\) ceros entonces\(c_1=c_2=\cdots=c_n=0\).
Encuentre la solución general de
\[\label{eq:9.2.18} y'''+3y''+3y'+y=0.\]
Solución
El polinomio característico de la Ecuación\ ref {eq:9.2.18} es
\[p(r)=r^3+3r^2+3r+1=(r+1)^3. \nonumber\]
Por lo tanto, la ecuación\ ref {eq:9.2.18} puede escribirse como
\[(D+1)^3y=0, \nonumber\]
así Teorema 9.2.1 implica que la solución general de la Ecuación\ ref {eq:9.2.18} es
\[y=e^{-x}(c_1+c_2x+c_3x^2). \nonumber\]
La prueba del siguiente teorema se esboza en el Ejercicio 9.2.41.
Si\(\omega \ne0\) y\(m\) es un entero positivo, entonces
\[\begin{array}{rl} \{e^{\lambda x}\cos\omega x, xe^{\lambda x}\cos\omega x, &\dots, x^{m-1}e^{\lambda x}\cos\omega x,\\ e^{\lambda x}\sin\omega x, xe^{\lambda x}\sin\omega x,& \dots, x^{m-1}e^{\lambda x}\sin\omega x\} \end{array}\nonumber \]
es un conjunto fundamental de soluciones de
\[[(D-\lambda)^2+\omega^2]^my=0. \nonumber\]
Encuentre la solución general de
\[\label{eq:9.2.19} (D^2+4D+13)^3y=0.\]
Solución
El polinomio característico de la Ecuación\ ref {eq:9.2.19} es
\[p(r)=(r^2+4r+13)^3=\left((r+2)^2+9\right)^3. \nonumber\]
Por lo tanto, la ecuación\ ref {eq:9.2.19} puede escribirse como
\[[(D+2)^2+9]^3y=0, \nonumber\]
así Teorema 9.2.2 implica que la solución general de la Ecuación\ ref {eq:9.2.19} es
\[y=(a_1+a_2x+a_3x^2)e^{-2x}\cos3x +(b_1+b_2x+b_3x^2)e^{-2x}\sin3x. \nonumber\]
Encuentre la solución general de
\[\label{eq:9.2.20} y^{(4)}+4y'''+6y''+4y'=0.\]
Solución
El polinomio característico de la Ecuación\ ref {eq:9.2.20} es
\[\begin{aligned} p(r)&=r^4+4r^3+6r^2+4r\\ &=r(r^3+4r^2+6r+4)\\ &=r(r+2)(r^2+2r+2)\\ &=r(r+2)[(r+1)^2+1].\end{aligned}\nonumber \]
Por lo tanto, la ecuación\ ref {eq:9.2.20} puede escribirse como
\[[(D+1)^2+1](D+2)Dy=0. \nonumber\]
Conjuntos fundamentales de soluciones de
\[\left[(D+1)^2+1\right] y=0,\quad (D+2) y=0,\quad \text{and} \quad Dy=0. \nonumber\]
están dadas por
\[\{e^{-x}\cos x,e^{-x}\sin x\},\quad \{e^{-2x}\},\quad \text{and} \quad \{1\}, \nonumber\]
respectivamente. Por lo tanto, la solución general de la Ecuación\ ref {eq:9.2.20} es
\[y=e^{-x}(c_1\cos x+c_2\sin x)+c_3e^{-2x}+c_4. \nonumber\]
Encuentre un conjunto fundamental de soluciones de
\[\label{eq:9.2.21} [(D+1)^2+1]^2(D-1)^3(D+1)D^2y=0.\]
Solución
Se puede obtener un conjunto fundamental de soluciones de Ecuación\ ref {eq:9.2.21} combinando conjuntos fundamentales de soluciones de
- \(\left[(D+1)^{2}+1\right]^{2} y=0\)
- \((D-1)^{3} y=0\)
- \((D+1) y=0\)
- \(D^{2} y=0\)
Los conjuntos fundamentales de soluciones de estas ecuaciones vienen dados por
- \(\{e^{-x} \cos x, x e^{-x} \cos x, e^{-x} \sin x, x e^{-x} \sin x\}\)
- \(\left\{e^{x}, x e^{x}, x^{2} e^{x}\right\}\)
- \(\left\{e^{-x}\right\}\),
- \(\{1, x\}\)
respectivamente. Estas diez funciones forman un conjunto fundamental de soluciones de Ecuación\ ref {eq:9.2.21}.


