11.3: Serie II de Fourier
- Page ID
- 115059
En esta sección discutimos las expansiones de Fourier en términos de las funciones propias de los Problemas 1-4 para la Sección 11.1.
Serie de coseno de Fourier
Del Ejercicio 11.1.20, las funciones propias
\[1,\, \cos{\pi x\over L}, \, \cos{2\pi x\over L},\dots, \, \cos{n\pi x\over L},\dots\nonumber \]
del problema del valor límite
\[\label{eq:11.3.1} y''+\lambda y=0,\quad y'(0)=0,\quad y'(L)=0\]
(Problema 2) son ortogonales en\([0,L]\). Si\(f\) es integrable\([0,L]\) entonces la expansión de Fourier de\(f\) en términos de estas funciones se llama la serie coseno de Fourier de\(f\) on\([0,L]\). Esta serie es
\[a_0+\sum_{n=1}^\infty a_n\cos{n\pi x\over L},\nonumber \]
donde
\[a_0={\int_0^Lf(x)\,dx\over\int_0^L\,dx}={1\over L}\int_0^Lf(x)\,dx\nonumber \]
y
\[a_n={\displaystyle\int_0^Lf(x)\cos{n\pi x\over L}\,dx\over\int_0^L \cos^2{n\pi x\over L}\,dx}={2\over L}\displaystyle\int_0^Lf(x)\cos{n\pi x\over L}\,dx,\quad n=1,2,3,\dots.\nonumber \]
Al comparar esta definición con el Teorema 11.2.6a se muestra que la serie coseno de Fourier de\(f\) on\([0,L]\) es la serie de Fourier de la función
\[f_{1}(x)=\left\{\begin{array}{cc}{f(-x),}&{-L<x<0,}\\{f(x),}&{}0\leq x\leq L\end{array} \right.\nonumber\]
obtenido\(f\) extendiéndose\([-L,L]\) como una función par (Figura 11.3.1 ).
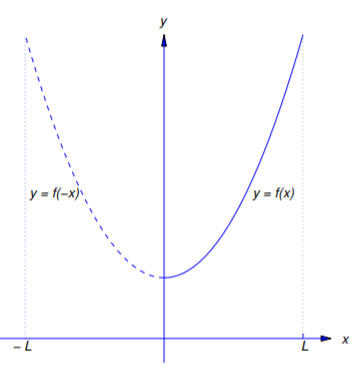
Aplicando el Teorema 11.2.4 para\(f_1\) arroja el siguiente teorema.
Si\(f\) es uniforme por partes\([0,L]\), entonces la serie de coseno de Fourier
\[C(x)=a_0+\sum_{n=1}^\infty a_n\cos{n\pi x\over L}\nonumber \]
de\(f\) on\([0,L]\), con
\[a_0={1\over L}\int_0^Lf(x)\,dx \quad \text{and} \quad a_n={2\over L}\int_0^Lf(x)\cos{n\pi x\over L}\,dx,\quad n=1,2,3,\dots,\nonumber \]
converge para todos\(x\) por\([0,L];\) otra parte,
\[C(x)=\left\{\begin{array}{cl}{f(0+),}&{\text{if }x=0}\\[5pt]{f(x),}&{\text{if } 0<x<L\text{ and }f \text{ is continuous at }x}\\[5pt]{\dfrac{f(x-)+f(x+)}{2},}&{\text{if }0<x<L\text{ and }f\text{ is discontinuous at }x}\\[5pt]{f(L-),}&{\text{if }x=L}\end{array} \right. \nonumber\]
Encuentra la serie de coseno de Fourier\(f(x)=x\) en\([0,L]\).
Los coeficientes son
\[a_0={1\over L}\int_0^Lx\,dx=\left. {1\over L}{x^2\over2} \right|_{0}^{L}={L\over2}\nonumber \]
y, si\(n\ge1\)
\[\begin{aligned} a_n&={2\over L}\int_0^Lx\cos{n\pi x\over L}\,dx =\left. {2\over n\pi}\left[x\sin{n\pi x\over L}\right|_{0}^{L}- \int_0^L \sin{n\pi x\over L}\,dx\right]\\ &=-{2\over n\pi}\int_0^L \sin{n\pi x\over L}\,dx =\left.{2L\over n^2\pi^2}\cos{n\pi x\over L}\right|_{0}^{L} ={2L\over n^2\pi^2}[(-1)^n-1]\\ &= \left\{\begin{array}{cl} -{4L\over(2m-1)^2\pi^2},&{\text{if }n=2m-1},\\ 0,&{\text{if }n=2m}. \end{array}\right.\end{aligned}\nonumber \]
Por lo tanto
\[C(x)=\frac{L}{2}-\frac{4L}{\pi ^{2}}\sum _{n=1}^{\infty}\frac{1}{(2n-1)^{2}}\cos\frac{(2n-1)\pi x}{L}\nonumber\]
El teorema 11.3.1 implica que
\[C(x)=x,\quad 0\le x\le L.\nonumber \]
Serie de seno de Fourier
Del Ejercicio 11.1.19, las funciones propias
\[\sin{\pi x\over L}, \, \sin{2\pi x\over L},\dots, \, \sin{n\pi x\over L},\dots\nonumber \]
del problema del valor límite
\[y''+\lambda y=0,\quad y(0)=0,\quad y(L)=0\nonumber \]
(Problema 1) son ortogonales en\([0,L]\). Si\(f\) es integrable\([0,L]\) entonces la expansión de Fourier de\(f\) en términos de estas funciones se llama la serie sinusoidal de Fourier de\(f\) on\([0,L]\). Esta serie es
\[\sum_{n=1}^\infty b_n\sin{n\pi x\over L},\nonumber \]
donde
\[b_n={\displaystyle\int_0^Lf(x)\sin{n\pi x\over L}\,dx\over\displaystyle\int_0^L \sin^2{n\pi x\over L}\,dx}={2\over L}\int_0^Lf(x)\sin{n\pi x\over L}\,dx,\quad n=1,2,3,\dots.\nonumber \]
La comparación de esta definición con el Teorema 11.2.6b muestra que la serie sinusoidal de Fourier de\(f\) on\([0,L]\) es la serie de Fourier de la función
\[f_{2}(x)=\left\{\begin{array}{cc}{-f(-x),}&{-L<x<0}\\{f(x),}&{0\leq x\leq L,}\end{array} \right.\nonumber\]
obtenido\(f\) extendiéndose\([-L,L]\) como una función impar (Figura 11.3.2 ).
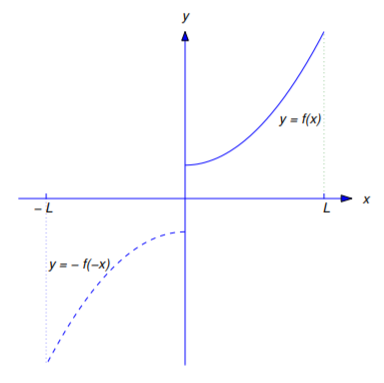
Aplicando el Teorema 11.2.4 para\(f_2\) arroja el siguiente teorema.
Si\(f\) es uniforme por partes\([0,L]\), entonces la serie sinusoidal de Fourier
\[S(x)=\sum_{n=1}^\infty b_n\sin{n\pi x\over L}\nonumber \]
de\(f\) on\([0,L]\), con
\[b_n={2\over L}\int_0^Lf(x)\sin{n\pi x\over L}\,dx,\nonumber \]
converge para todos\(x\) por\([0,L];\) otra parte,
\[S(x)=\left\{\begin{array}{cl}{0}&{\text{if }x=0}\\[5pt]{f(x),}&{\text{if }0<x<L\text{ and }f\text{ is continuous at }x}\\[5pt]{\dfrac{f(x-)+f(x+)}{2},}&{\text{if }0<x<L\text{ and }f\text{ is discontinuous at }x}\\[5pt]{0,}&{\text{if }x=L}\end{array} \right.\nonumber\]
Encuentra la serie sinusoidal de Fourier de\(f(x)=x\) on\([0,L]\).
Solución
Los coeficientes son
\[\begin{aligned} b_n&={2\over L}\int_0^Lx\sin{n\pi x\over L}\,dx =\left.-{2\over n\pi}\left[x\cos{n\pi x\over L}\right|_{0}^{L}- \int_0^L \cos{n\pi x\over L}\,dx\right]\\ &=\left. (-1)^{n+1}{2L\over n\pi}+{2L\over n^2\pi^2}\sin{n\pi x\over L}\right|_{0}^{L} =(-1)^{n+1}{2L\over n\pi}.\end{aligned}\nonumber \]
Por lo tanto
\[S(x)=-{2L\over\pi}\sum_{n=1}^\infty{(-1)^n\over n} \sin{n\pi x\over L}.\nonumber \]
El teorema 11.3.2 implica que
\[S(x)= \left\{\begin{array}{cl} x,&0\le x< L,\\0,& x=L. \end{array}\right.\nonumber \]
Serie mixta de coseno de Fourier
Del Ejercicio 11.1.22, las funciones propias
\[\cos{\pi x\over 2L}, \, \cos{3\pi x\over 2L},\dots, \, \cos{(2n-1)\pi x\over 2L},\dots\nonumber \]
del problema del valor límite
\[\label{eq:11.3.2} y''+\lambda y=0,\quad y'(0)=0,\quad y(L)=0\]
(Problema 4) son ortogonales en\([0,L]\). Si\(f\) es integrable en\([0,L]\) entonces la expansión de Fourier\(f\) en términos de estas funciones es
\[\sum_{n=1}^\infty c_n\cos{(2n-1)\pi x\over2L},\nonumber \]
donde
\[c_n={\displaystyle\int_0^Lf(x)\cos{(2n-1)\pi x\over2L}\,dx\over\displaystyle\int_0^L \cos^2{(2n-1)\pi x\over L}\,dx}={2\over L}\int_0^Lf(x)\cos{(2n-1)\pi x\over2L}\,dx.\nonumber \]
Llamaremos a esta expansión la serie mixta de coseno de Fourier de\(f\) on\([0,L]\), porque las condiciones límite de (Ecuación\ ref {eq:11.3.2}) son “mixtas” en que requieren\(y\) ser cero en un punto límite y\(y'\) ser cero en el otro. Por el contrario, la serie “ordinaria” de coseno de Fourier está asociada con (Ecuación\ ref {eq:11.3.1}), donde las condiciones límite requieren que\(y'\) sea cero en ambos puntos finales.
Se puede demostrar (Ejercicio 11.3.57) que la serie mixta de coseno de Fourier de\(f\) on\([0,L]\) es simplemente la restricción a\([0,L]\) de la serie coseno de Fourier de
\[f_3(x)= \left\{\begin{array}{cl} f(x),&0\le x\le L,\\-f(2L-x),&L< x\le 2L \end{array}\right.\nonumber \]
on\([0,2L]\) (Figura 11.3.3 ).
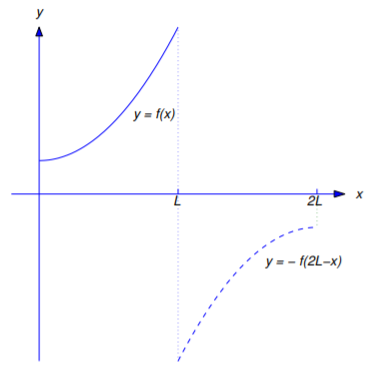
Aplicando el teorema 11.3.1 con\(f\) reemplazado por\(f_3\) y\(L\) reemplazado por\(2L\) rinde el siguiente teorema.
Si\(f\) se suaviza por partes\([0,L]\), entonces la serie mixta de coseno de Fourier
\[C_M(x)=\sum_{n=1}^\infty c_n\cos{(2n-1)\pi x\over2L}\nonumber \]
de\(f\) on\([0,L]\), con
\[c_n={2\over L}\int_0^Lf(x)\cos{(2n-1)\pi x\over2L}\,dx,\nonumber \]
converge para todos\(x\) por\([0,L];\) otra parte,
\[C_{M}(x)=\left\{\begin{array}{cl}{f(0+),}&{\text{if }x=0}\\[5pt]{f(x),}&{\text{if }0<x<L\text{ and }f\text{ is continuous at }x}\\[5pt]{\dfrac{f(x-)+f(x+)}{2},}&{\text{if }0<x<L\text{ and }f\text{ is discontinuous at }x}\\[5pt]{0,}&{\text{if }x=L}\end{array} \right.\nonumber\]
Encuentra la serie mixta de coseno de Fourier de\(f(x)=x-L\) on\([0,L]\).
Solución
Los coeficientes son
\[\begin{aligned} c_n&={2\over L}\int_0^L(x-L)\cos{(2n-1)\pi x\over2L}\,dx\\ &=\left.{4\over(2n-1)\pi}\left[(x-L)\sin{(2n-1)\pi x\over2L}\right|_{0}^{L}-\int_0^L \sin{(2n-1)\pi x\over2L}\,dx\right]\\ &=\left.{8L\over(2n-1)^2\pi^2} \cos{(2n-1)\pi x\over2L}\right|_{0}^{L} =-{8L\over(2n-1)^2\pi^2}.\end{aligned}\nonumber \]
Por lo tanto
\[C_M(x)=-{8L\over\pi^2}\sum_{n=1}^\infty{1\over(2n-1)^2} \cos{(2n-1)\pi x\over2L}.\nonumber \]
El teorema 11.3.3 implica que
\[C_M(x)= x-L,\quad 0\le x\le L.\nonumber \]
Serie mixta de seno de Fourier
Del Ejercicio 11.1.21, las funciones propias
\[\sin{\pi x\over 2L}, \, \sin{3\pi x\over 2L},\dots, \, \sin{(2n-1)\pi x\over 2L},\dots\nonumber \]
del problema del valor límite
\[y''+\lambda y=0,\quad y(0)=0,\quad y'(L)=0\nonumber \]
(Problema 3) son ortogonales en\([0,L]\). Si\(f\) es integrable\([0,L]\), entonces la expansión de Fourier\(f\) en términos de estas funciones es
\[\sum_{n=1}^\infty d_n\sin{(2n-1)\pi x\over2L},\nonumber \]
donde
\[d_n={\displaystyle\int_0^Lf(x)\sin{(2n-1)\pi x\over2L}\,dx\over\displaystyle\int_0^L \sin^2{(2n-1)\pi x\over2L}\,dx}={2\over L}\int_0^Lf(x)\sin{(2n-1)\pi x\over2L}\,dx.\nonumber \]
Llamaremos a esta expansión la serie sinusoidal mixta de Fourier\(f\) on\([0,L]\).
Se puede demostrar (Ejercicio 11.3.58) que la serie de seno mixto de Fourier de\(f\) on\([0,L]\) es simplemente la restricción a\([0,L]\) de la serie sinusoidal de Fourier de
\[f_4(x)= \left\{\begin{array}{cl} f(x),&0\le x\le L,\\f(2L-x),&L< x\le 2L, \end{array}\right.\nonumber \]
on\([0,2L]\) (Figura 11.3.4 ).
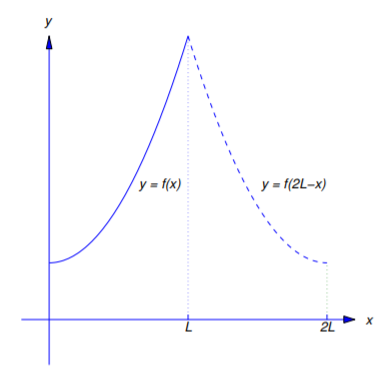
Aplicando el teorema 11.3.2 con\(f\) reemplazado por\(f_4\) y\(L\) reemplazado por\(2L\) rinde el siguiente teorema.
Si\(f\) es uniforme por partes\([0,L]\), entonces la serie sinusoidal mixta de Fourier
\[S_M(x)=\sum_{n=1}^\infty d_n\sin{(2n-1)\pi x\over2L}\nonumber \]
de\(f\) on\([0,L]\), con
\[d_n={2\over L}\int_0^Lf(x)\sin{(2n-1)\pi x\over2L}\,dx,\nonumber \]
converge para todos\(x\) por\([0,L];\) otra parte,
\[S{M}(x)=\left\{\begin{array}{cl}{0,}&{\text{if }x=0}\\[5pt]{f(x),}&{\text{if }0<x<L\text{ and }f\text{ is continuous at }x}\\[5pt]{\dfrac{f(x-)+f(x+)}{2},}&{\text{if }0<x<L\text{ and }f\text{ is discontinuous at }x}\\[5pt]{f(L-),}&{\text{if }x=L}\end{array} \right.\nonumber\]
Encuentra la serie de seno mixto de Fourier de\(f(x)=x\) on\([0,L]\).
Solución
Los coeficientes son
\[\begin{aligned} d_n&={2\over L}\int_0^Lx\sin{(2n-1)\pi x\over2L}\,dx\\ &=\left.-{4\over(2n-1)\pi}\left[x\cos{(2n-1)\pi x\over2L}\right|_{0}^{L}- \int_0^L \cos{(2n-1)\pi x\over2L}\,dx\right]\\ &={4\over(2n-1)\pi} \int_0^L \cos{(2n-1)\pi x\over2L}\,dx\\ &=\left.{8L\over(2n-1)^2\pi^2}\sin{(2n-1)\pi x\over2L}\right|_{0}^{L}=(-1)^{n+1}{8L\over(2n-1)^2\pi^2}.\end{aligned}\nonumber \]
Por lo tanto
\[S_M(x)=-{8L\over\pi^2}\sum_{n=1}^\infty{(-1)^n\over(2n-1)^2} \sin{(2n-1)\pi x\over2L}.\nonumber \]
El teorema 11.3.4 implica que
\[S_M(x)=x,\quad 0\le x\le L.\nonumber \]
Una observación útil
En aplicaciones que involucran expansiones en términos de las funciones propias de los Problemas 1-4, las funciones que se expanden suelen ser polinomios que satisfacen las condiciones límite del problema en consideración. En este caso el siguiente teorema presenta una manera eficiente de obtener los coeficientes en la expansión.
- Si\(f'(0)=f'(L)=0\),\(f''\) es continuo\(,\) y\(f'''\) es continuo por piezas\([0,L],\) entonces\[\label{eq:11.3.3} f(x)=a_0+\sum_{n=1}^\infty a_n\cos{n\pi x\over L}, \quad 0\le x\le L,\] con\[\label{eq:11.3.4} a_0={1\over L}\int_0^L f(x)\,dx \quad \text{and} \quad a_n= {2L^2\over n^3\pi^3}\int_0^L f'''(x)\sin{n\pi x\over L}\,dx, \quad n\ge1.\] Ahora supongamos que\(f'\) es continuo y\(f''\) es continuo por partes en\([0,L].\)
- Si\(f(0)=f(L)=0\), entonces\[f(x)=\sum_{n=1}^\infty b_n\sin{n\pi x\over L}, \quad 0\le x\le L,\nonumber \] con\[\label{eq:11.3.5} b_n=-{2L\over n^2\pi^2}\int_0^L f''(x)\sin{n\pi x\over L}\,dx.\]
- Si\(f'(0)=f(L)=0\), entonces\[f(x)= \sum_{n=1}^\infty c_n\cos{(2n-1)\pi x\over2L}, \quad 0\le x\le L,\nonumber \] con\[\label{eq:11.3.6} c_n=-{8L\over(2n-1)^2\pi^2}\int_0^L f''(x)\cos{(2n-1)\pi x\over2L} \,dx.\]
- Si\(f(0)=f'(L)=0\), entonces\[f(x)= \sum_{n=1}^\infty d_n\sin{(2n-1)\pi x\over2L}, \quad 0\le x\le L,\nonumber \] con\[\label{eq:11.3.7} d_n=-{8L\over(2n-1)^2\pi^2}\int_0^L f''(x)\sin{(2n-1)\pi x\over2L} \,dx.\]
- Prueba
-
Te probaremos (a) y te dejaremos el resto (Ejercicios 11.3.35, 11.3.42 y 11.3.50). Dado que\(f\) es continuo en\([0,L]\), Teorema 11.3.1 implica (Ecuación\ ref {eq:11.3.3}) con\(a_0\),,\(a_1\)\(a_2\),... como se define en el Teorema 11.3.1 . Ya sabemos que\(a_0\) es como en (Ecuación\ ref {eq:11.3.4}). Si\(n\ge1\), integrando dos veces por partes rinde
\[\begin{aligned} a_n&= {2\over L}\int_0^L f(x)\cos{n\pi x\over L}\,dx\\ &=\left.{2\over n\pi}\left[f(x)\sin{n\pi x\over L}\right|_{0}^{L} -\int_0^Lf'(x)\sin{n\pi x\over L}\,dx\right]\\ &=-{2\over n\pi} \int_0^Lf'(x)\sin{n\pi x\over L}\,dx \mbox{ (since $\sin0=\sin n\pi=0$)}\\ &=\left.{2L\over n^2\pi^2}\left[f'(x)\cos{n\pi x\over L}\right|_{0}^{L} -\int_0^Lf''(x)\cos{n\pi x\over L}\right]\,dx\\ &= -{2L\over n^2\pi^2}\int_0^Lf''(x)\cos{n\pi x\over L}\,dx \mbox{ (since $f'(0)=f'(L)=0$)}\\ &=\left.-{2L^2\over n^3\pi^3}\left[f''(x)\sin{n\pi x\over L}\right|_{0}^{L} -\int_0^Lf'''(x)\sin{n\pi x\over L}\,dx\right]\\ &= {2L^2\over n^3\pi^3}\int_0^Lf'''(x)\sin{n\pi x\over L}\,dx \mbox{ (since $\sin0=\sin n\pi=0$).}\end{aligned}\nonumber \]
(Por un argumento similar al utilizado en la prueba del Teorema 8.3.1, la última integración por partes es legítima en el caso en el que\(f'''\) está indefinido en finitamente muchos puntos en\([0,L]\), siempre y cuando sea continuo por partes en\([0,L]\).) Esto completa la prueba.
Encuentre la expansión del coseno de Fourier de\(f(x)=x^2(3L-2x)\) on\([0,L]\).
Solución
Aquí
\[a_0={1\over L}\int_0^L(3Lx^2-2x^3)\,dx=\left.{1\over L}\left(Lx^3-{x^4\over2} \right)\right|_{0}^{L}={L^3\over2}\nonumber \]
y
\[a_n={2\over L}\int_0^L(3Lx^2-2x^3)\cos{n\pi x\over L}\,dx,\quad n\ge1.\nonumber \]
Evaluar esta integral directamente es laborioso. No obstante, ya que\(f'(x)=6Lx-6x^2\), vemos eso\(f'(0)=f'(L)=0\). Ya que\(f'''(x)=-12\), vemos de (Ecuación\ ref {eq:11.3.4}) que si\(n\ge1\) entonces
\[\begin{aligned} a_n&=-{24L^2\over n^3\pi^3}\int_0^L\sin{n\pi x\over L}\,dx =\left.{24L^3\over n^4\pi^4}\cos{n\pi x\over L}\right|_{0}^{L}={24L^3\over n^4\pi^4}[(-1)^n-1]\\ &= \left\{\begin{array}{cl} -{48L^3\over(2m-1)^4\pi^4},&\mbox{if $n=2m-1$},\\ 0,&\mbox{if $n=2m$.} \end{array}\right.\end{aligned}\nonumber \]
Por lo tanto
\[C(x)={L^3\over2}-{48L^3\over\pi^4}\sum_{n=1}^\infty{1\over (2n-1)^4}\cos{(2n-1)\pi x\over L}.\nonumber \]
Encuentre la expansión sinusoidal de Fourier de\(f(x)=x(x^2-3Lx+2L^2)\) on\([0,L]\).
Solución
Desde\(f(0)=f(L)=0\) y\(f''(x)=6(x-L)\), vemos desde (Ecuación\ ref {eq:11.3.5}) que
\[\begin{aligned} b_n&=- {12L\over n^2\pi^2}\int_0^L(x-L)\sin{n\pi x\over L}\,dx\\ &=\left.{12L^2\over n^3\pi^3}\left[(x-L)\cos{n\pi x\over L}\right|_{0}^{L} -\int_0^L\cos{n\pi x\over L}\,dx\right]\\ &=\left.{12L^2\over n^3\pi^3}\left[L-\frac{L}{n\pi}\sin\frac{n\pi x}{L}\right|_{0}^{L}\right] ={12L^3\over n^3\pi^3}.\end{aligned}\nonumber \]
Por lo tanto
\[S(x)=\frac{12L^{3}}{\pi ^{3}}\sum_{n=1}^{\infty}\frac{1}{n^{3}}\sin\frac{n\pi x}{L}\nonumber\]
Encuentre la expansión mixta de coseno de Fourier de\(f(x)=3x^3-4Lx^2+L^3\) on\([0,L]\).
Solución
Desde\(f'(0)=f(L)=0\) y\(f''(x)=2(9x-4L)\), vemos desde (Ecuación\ ref {eq:11.3.6}) que
\[\begin{aligned} c_n&= -{16L\over(2n-1)^2\pi^2} \int_0^L(9x-4L)\cos{(2n-1)\pi x\over2L}\,dx\\ &=\left.-{32L^2\over(2n-1)^3\pi^3}\left[(9x-4L)\sin{(2n-1)\pi x\over2L} \right|_{0}^{L}-9\int_0^L\sin{(2n-1)\pi x\over2L}\right]\,dx\\ &=\left.-{32L^2\over(2n-1)^3\pi^3} \left[(-1)^{n+1}5L+{18L\over(2n-1)\pi}\cos{(2n-1)\pi x\over2L} \right|_{0}^{L}\right] \\ &={32L^3\over(2n-1)^3\pi^3} \left[(-1)^n5+{18\over(2n-1)\pi}\right].\end{aligned}\nonumber \]
Por lo tanto
\[C_{M}(x)=\frac{32L^{3}}{\pi ^{3}}\sum_{n=1}^{\infty}\frac{1}{(2n-1)^{3}}\left[(-1)^{n}5+\frac{18}{(2n-1)\pi } \right]\cos\frac{(2n-1)\pi x}{2L}\nonumber\]
Encuentre la expansión sinusoidal mixta de Fourier
\[f(x)=x(2x^2-9Lx+12L^2)\nonumber \]
encendido\([0,L]\).
Solución
Desde\(f(0)=f'(L)=0\), y\(f''(x)=6(2x-3L)\), vemos a partir de (Ecuación\ ref {eq:11.3.7}) que
\[\begin{aligned} d_{n}&=-\frac{48L}{(2n-1)^{2}\pi ^{2}}\int_{0}^{L}(2x-3L)\sin\frac{(2n-1)\pi x}{2L}dx \\ &=\left.\frac{96L^{2}}{(2n-1)^{3}\pi ^{3}}\left[(2x-3L)\cos\frac{(2n-1)\pi x}{2L}\right|_{0}^{L} - 2\int_{0}^{L}\cos\frac{(2n-1)\pi x}{2L}dx \right] \\ &=\left. \frac{96L^{2}}{(2n-1)^{3}\pi ^{3}}\left[3L-\frac{4L}{(2n-1)\pi }\sin\frac{(2n-1)\pi x}{2L}\right|_{0}^{L} \right] \\&=\frac{96L^{3}}{(2n-1)^{3}\pi ^{3}}\left[3+(-1)^{n}\frac{4}{(2n-1)\pi } \right] \end{aligned}\nonumber\]
Por lo tanto
\[S_{M}(x)=\frac{96L^{3}}{\pi ^{3}}\sum_{n=1}^{\infty}\frac{1}{(2n-1)^{3}}\left[3+(-1)^{n}\frac{4}{(2n-1)\pi } \right]\sin\frac{(2n-1)\pi x}{2L}\nonumber\]


