11.2E: Serie I de Fourier (Ejercicios)

Q11.2.1

1. Demostrar Teorema 11.1.5.

Q11.2.2

En Ejercicios 11.2.2-11.2.16 encontrar la serie de Fourier de\(f\) on\([-L,L]\) y determinar su suma para\(-L\leq x\leq L\). Gráfica\(f\) para los Ejercicios 11.2.2, 11.2.6, 11.2.8, 11.2.15, y 11.2.16 y\[F_{m}(x)=a_{0}+\sum _{n=1}^{m}\left( a_{n}\cos\frac{n\pi x}{L}+b_{n}\sin\frac{n\pi x}{L} \right)\nonumber \] en los mismos ejes para valores variables de\(m\).

2. \(L=1\);\(f(x)=2-x\)

3. \(L=\pi\);\(f(x)=2x-3x^2\)

4. \(L=1\);\(f(x)=1-3x^2\)

5. \(L=\pi\);\(f(x)=|\sin x|\)

6. \(L=\pi\);\(f(x)=x\cos x\)

7. \(L=\pi\);\(f(x)=|x|\cos x\)

8. \(L=\pi\);\(f(x)=x\sin x\)

9. \(L=\pi\);\(f(x)=|x|\sin x\)

10. \(L=1\);\(f(x)= \left\{\begin{array}{cl} 0,&-1<x<{1\over2},\\ \cos\pi x,&-{1\over2}<x<{1\over2},\\ 0,&\phantom{-}{1\over2}<x<1 \end{array}\right.\)

11. \(L=1\);\(f(x)= \left\{\begin{array}{cl} 0,&-1<x<{1\over2},\\ x\cos\pi x,&-{1\over2}<x<{1\over2},\\ 0,&\phantom{-}{1\over2}<x<1 \end{array}\right.\)

12. \(L=1\);\(f(x)= \left\{\begin{array}{cl} 0,&-1<x<{1\over2},\\ \sin\pi x,&-{1\over2}<x<{1\over2},\\ 0,&\phantom{-}{1\over2}<x<1 \end{array}\right.\)

13. \(L=1\);\(f(x)= \left\{\begin{array}{cl} 0,&-1<x<{1\over2},\\ |\sin\pi x|,&-{1\over2}<x<{1\over2},\\ 0,&\phantom{-}{1\over2}<x<1 \end{array}\right.\)

14. \(L=1\);\(f(x)= \left\{\begin{array}{cl} 0,&-1<x<{1\over2},\\ x\sin\pi x,&-{1\over2}<x<{1\over2},\\ 0,&\phantom{-}{1\over2}<x<1 \end{array}\right.\)

15. \(L=4\);\(f(x)= \left\{\begin{array}{cl} 0,&-4<x<0,\\x,&\phantom{-}0<x<4 \end{array}\right.\)

16. \(L=1\);\(f(x)= \left\{\begin{array}{cl} x^2,&-1< x<0, \\1-x^2,&\phantom{-}0<x<1 \end{array}\right.\)

Q11.2.3

17. Verificar el fenómeno Gibbs para\(f(x)= \left\{\begin{array}{rl} 2,&-2< x< -1,\\1,&-1<x<1,\\-1,&\phantom{-}1< x<2. \end{array}\right.\)

18. Verificar el fenómeno Gibbs para\(f(x)= \left\{\begin{array}{rl} 2,&-3< x< -2,\\3,&-2<x<2,\\1,&\phantom{-}2< x<3. \end{array}\right.\)

19. Deducir del Ejemplo 11.2.5 que

\[\sum_{n=0}^\infty{1\over(2n+1)^2}={\pi^2\over 8}.\nonumber \]

20.

1. Encuentre la serie de Fourier de\(f(x)=e^x\) en\([-\pi,\pi]\).
2. Deducir de (a) que\[\sum_{n=0}^\infty{1\over n^2+1}={\pi\coth\pi-1\over2}.\nonumber \]

21. Encuentre la serie de Fourier de\(f(x)=(x-\pi)\cos x\) en\([-\pi,\pi]\).

22. Encuentre la serie de Fourier de\(f(x)=(x-\pi)\sin x\) en\([-\pi,\pi]\).

23. Encuentra la serie de Fourier de\(f(x)=\sin kx\) (\(k\ne\)entero) en\([-\pi,\pi]\).

24. Encuentra la serie de Fourier de\(f(x)=\cos kx\) (\(k\ne\)entero) en\([-\pi,\pi]\).

25.

1. Supongamos que\(g'\) es continuo en\([a,b]\) y\(\omega\ne0\). Usa la integración por partes para demostrar que hay una constante\(M\) tal que\[\left|\int_a^bg(x)\cos\omega x\,dx\right|\le{M\over\omega} \quad \text{and} \quad \left|\int_a^bg(x)\sin\omega x\,dx\right|\le{M\over\omega},\quad \omega>0.\nonumber\]
2. Demostrar que la conclusión de (a) también se sostiene si\(g\) es poco suave en\([a,b]\). (Este es un caso especial del Lemma de Riemann.
3. Decimos que una secuencia\(\{\alpha_n\}_{n=1}^\infty\) es de orden\(n^{-k}\) y escribimos\(\alpha_n=O(1/n^k)\) si hay una constante\(M\) tal que\[|\alpha_n|<{M\over n^k},\quad n=1,2,3,\dots.\nonumber \] Let\(\{a_n\}_{n=1}^\infty\) y\(\{b_n\}_{n=1}^\infty\) ser los coeficientes de Fourier de una función lisa por partes. Concluir de (b) que\(a_n=O(1/n)\) y\(b_n=O(1/n)\).

26.

1. Supongamos\(f(-L)=f(L)\)\(f'(-L)=f'(L)\),,\(f'\) es continuo, y\(f''\) es continuo por partes en\([-L,L]\). Utilice el Teorema 11.2.4 y la integración por partes para mostrar que\[f(x)=a_0+\sum_{n=1}^\infty\left(a_n\cos{n\pi x\over L}+b_n\sin{n\pi x\over L}\right),\quad -L\le x\le L,\nonumber \] con\[a_0={1\over 2L}\int_{-L}^L f(x)\,dx,\nonumber \]\[a_n= -{L\over n^2\pi^2}\int_{-L}^L f''(x)\cos{n\pi x\over L}\,dx,\quad \text{and} \quad b_n=-{L\over n^2\pi^2}\int_{-L}^L f''(x)\sin{n\pi x\over L}\,dx,\,n\ge1.\nonumber \]
2. Demostrar que si, además de los supuestos en (a),\(f''\)\(f'''\) es continuo y es continuo por partes\([-L,L]\), entonces\[a_n={L^2\over n^3\pi^3}\int_{-L}^Lf'''(x)\sin{n\pi x\over L}\,dx.\nonumber \]

27. Mostrar que si\(f\) es integrable on\([-L,L]\) y\[f(x+L)=f(x),\quad -L<x<0\nonumber \] (Figura 11.2.8), entonces la serie de Fourier de\(f\) on\([-L,L]\) tiene la forma\[A_0+\sum_{n=1}^\infty\left(A_n\cos{2n\pi\over L}+B_n\sin{2n\pi\over L}\right)\nonumber \] donde\[A_0={1\over L}\int_0^Lf(x)\,dx,\nonumber \] y\[A_n={2\over L}\int_0^Lf(x)\cos{2n\pi x\over L}\,dx, \quad B_n={2\over L}\int_0^Lf(x)\sin{2n\pi x\over L}\,dx,\quad n=1,2,3,\dots.\nonumber \]

Figura 11.2.8:\(y=f(x)\), donde\(f(x+L)=f(x), -L<x<0\)

Figura 11.2.9:\(y=f(x)\), donde\(f(x+L)=-f(x), -L<x<0\)

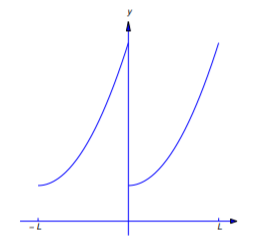
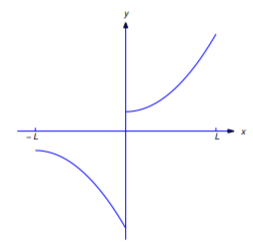
28. Mostrar que si\(f\) es integrable en\([-L,L]\) y

\[f(x+L)=-f(x),\quad -L<x<0\nonumber \]

(Figura 11.2.9), luego la serie de Fourier de\(f\) on\([-L,L]\) tiene la forma

\[\sum_{n=1}^\infty\left(A_n\cos{(2n-1)\pi x\over L}+B_n\sin{(2n-1)\pi x\over L}\right),\nonumber \]

donde

\[A_n={2\over L}\int_0^Lf(x)\cos{(2n-1)\pi x\over L}\,dx \quad \text{and} \quad B_n={2\over L}\int_0^Lf(x)\sin{(2n-1)\pi x\over L}\,dx,\quad n=1,2,3,\dots.\nonumber \]

29. Supongamos\(\phi_1\)\(\phi_2\),,...,\(\phi_m\) son ortogonales en\([a,b]\) y

\[\int_a^b\phi_n^2(x)\,dx\ne0,\quad n=1,2,\dots,m.\nonumber \]

Si\(a_1\),\(a_2\),...,\(a_m\) son números reales arbitrarios, defina

\[P_m=a_1\phi_1+a_2\phi_2+\cdots+a_m\phi_m.\nonumber \]

Let

\[F_m=c_1\phi_1+c_2\phi_2+\cdots+c_m\phi_m,\nonumber \]

donde

\[c_n={\int_a^bf(x)\phi_n(x)\,dx\over\int_a^b\phi_n^2(x)\,dx};\nonumber \]

es decir,\(c_1\),\(c_2\),...,\(c_m\) son coeficientes de Fourier de\(f\).

1. Demostrar que\[\int_a^b(f(x)-F_m(x))\phi_n(x)\,dx=0,\quad n=1,2,\dots,m.\nonumber \]
2. Demostrar eso\[\int_a^b(f(x)-F_m(x))^2\,dx\le \int_a^b(f(x)-P_m(x))^2\,dx,\nonumber \] con igualdad si y sólo si\(a_n=c_n\),\(n=1,2,\dots, m\).
3. Demostrar que\[\int_a^b(f(x)-F_m(x))^2\,dx=\int_a^bf^2(x)\,dx-\sum_{n=1}^mc_n^2\int_a^b \phi_n^2\,dx.\nonumber \]
4. Concluir de (c) que\[\sum_{n=1}^m c_n^2\int_a^b\phi_n^2(x)\,dx\le \int_a^bf^2(x)\,dx.\nonumber \]

30. Si\(A_0\),\(A_1\),...,\(A_m\) y\(B_1\),\(B_2\),...,\(B_m\) son constantes arbitrarias decimos que

\[P_m(x)=A_0+\sum_{n=1}^m\left(A_n\cos{n\pi x\over L}+B_n\sin{n\pi x\over L}\right)\nonumber \]

es un polinomio trigonométrico de grado\(\le m\).

Ahora vamos

\[a_0+\sum_{n=1}^\infty\left(a_n\cos{n\pi x\over L}+b_n\sin{n\pi x\over L}\right)\nonumber \]

ser la serie de Fourier de una función integrable\(f\) en\([-L,L]\), y dejar

\[F_m(x)= a_0+\sum_{n=1}^m\left(a_n\cos{n\pi x\over L}+b_n\sin{n\pi x\over L}\right).\nonumber \]

1. Concluir del Ejercicio 11.2.29b que\[\int_{-L}^L(f(x)-F_m(x))^2\,dx\le \int_{-L}^L(f(x)-P_m(x))^2\,dx,\nonumber \] con igualdad si y sólo si\(A_n=a_n\),\(n=0\),\(1\),,...\(m\), y\(B_n=b_n\),,\(n=1\),\(2\),...,\(m\).
2. Concluir del Ejercicio 11.2.29d que\[2a_0^2+\sum_{n=1}^m(a_n^2+b_n^2)\le{1\over L}\int_{-L}^Lf^2(x)\,dx\nonumber \] para cada\(m\ge0\).
3. Concluir de (b) que\(\lim_{n\to\infty}a_n=\lim_{n\to\infty}b_n=0\).