12.2: La Ecuación de Onda
- Page ID
- 114766
En esta sección consideramos problemas de valor inicial-límite de la forma
\[\label{eq:12.2.1} \begin{array}{c}{u_{tt}=a^{2}u_{xx},\quad 0<x<L,\quad t>0,}\\{u(0,t)=0,\quad u(L,t)=0,\quad t>0,}\\{u(x,0)=f(x),\quad u_{t}(x,0)=g(x),\quad 0\leq x\leq L,}\end{array}\]
donde\(a\) es una constante y\(f\) y\(g\) se les dan funciones de\(x\). La ecuación diferencial parcial\(u_{tt}=a^2u_{xx}\) se llama ecuación de onda. Es necesario especificar ambos\(f\) y\(g\) porque la ecuación de onda es una ecuación de segundo orden en\(t\) para cada fijo\(x\). Esta ecuación y sus generalizaciones
\[u_{tt}=a^2(u_{xx}+u_{yy}) \quad \text{and} \quad u_{tt}=a^2(u_{xx}+u_{yy}+u_{zz}) \nonumber \]
a dos y tres dimensiones espaciales tienen aplicaciones importantes para la propagación de ondas electromagnéticas, sónicas y de agua.
La Cuerda Vibradora
Motivamos el estudio de la ecuación de onda considerando su aplicación a las vibraciones de una cuerda —como una cuerda de violín— fuertemente estirada en equilibrio a lo largo del\(x\) eje\(xu\) -en el -plano y atada a los puntos\((0,0)\) y\((L,0)\) (Figura 12.2.1 ).

Si la cuerda es arrancada en dirección vertical y liberada en el momento\(t=0\), oscilará en el\(xu\) plano -plano. Dejar\(u(x,t)\) denotar el desplazamiento del punto en la cadena por encima (o por debajo) de la abscisa\(x\) en el momento\(t\).
Demostraremos que es razonable suponer que\(u\) satisface la ecuación de onda bajo los siguientes supuestos:
- La densidad de masa (masa por unidad de longitud)\(\rho\) de la cuerda es constante en toda la cuerda.
- La tensión\(T\) inducida por estirar fuertemente la cuerda a lo largo del\(x\) eje es tan grande que se pueden descuidar todas las demás fuerzas, como la gravedad y la resistencia al aire.
- La tensión en cualquier punto de la cuerda actúa a lo largo de la tangente a la cuerda en ese punto, y la magnitud de su componente horizontal siempre es igual a\(T\), la tensión en la cuerda en equilibrio.
- La pendiente de la cuerda en cada punto permanece lo suficientemente pequeña para que podamos hacer la aproximación\[\label{eq:12.2.2} \sqrt{1+u_x^2}\approx1.\]
La figura 12.2.2 muestra un segmento de la cadena desplazada a la vez\(t>0\). (No pienses que la cifra es necesariamente inconsistente con la Asunción 4; exageramos la pendiente para mayor claridad).
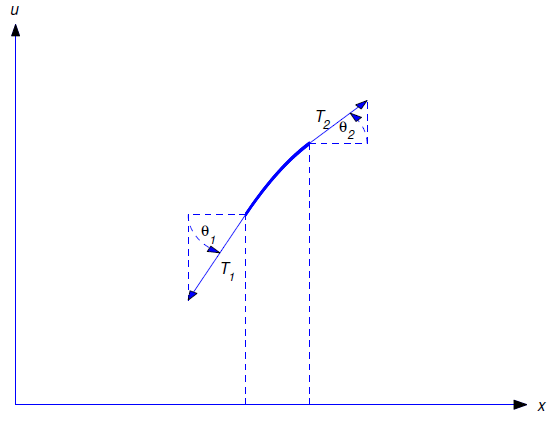
Los vectores\({\bf T}_1\) y\({\bf T}_2\) son las fuerzas debidas a la tensión, actuando a lo largo de las tangentes al segmento en sus extremos. De la segunda ley de movimiento de Newton,\({\bf T}_1-{\bf T}_2\) es igual a la masa multiplicada por la aceleración del centro de masa del segmento. Los componentes horizontales y verticales de\({\bf T}_1-{\bf T}_2\) son
\[|{\bf T}_2|\cos\theta_2- |{\bf T}_1|\cos\theta_1 \quad \text{and} \quad |{\bf T}_2|\sin\theta_2- |{\bf T}_1|\sin\theta_1, \nonumber \]
respectivamente. Desde
\[\label{eq:12.2.3} |{\bf T}_2|\cos\theta_2=|{\bf T}_1|\cos\theta_1=T\]
por supuesto, la fuerza horizontal neta es cero, por lo que no hay aceleración horizontal. Dado que la velocidad horizontal inicial es cero, no hay movimiento horizontal.
Aplicando la segunda ley de movimiento de Newton en la dirección vertical rinde
\[\label{eq:12.2.4} |{\bf T}_2|\sin\theta_2- |{\bf T}_1|\sin\theta_1=\rho\Delta s\,u_{tt}(\overline x,t),\]
donde\(\Delta s\) es la longitud del segmento y\(\overline x\) es la abscisa del centro de masa; por lo tanto,
\[x<\overline x <x+\Delta x.\nonumber\]
A partir del cálculo, sabemos que
\[\Delta s=\int_x^{x+\Delta x}\sqrt{1+u_x^2(\sigma,t)}\,d\sigma;\nonumber\]
sin embargo, debido a la Ecuación\ ref {eq:12.2.2}, hacemos la aproximación
\[\Delta s\approx\int_x^{x+\Delta x}1\,d\sigma=\Delta x,\nonumber\]
así que la ecuación\ ref {eq:12.2.4} se convierte
\[|{\bf T}_2|\sin\theta_2- |{\bf T}_1|\sin\theta_1=\rho\Delta x\,u_{tt}(\overline x,t).\nonumber\]
Por lo tanto
\[{|{\bf T}_2|\sin\theta_2- |{\bf T}_1|\sin\theta_1\over\Delta x}=\rho u_{tt}(\overline x,t).\nonumber\]
Recordando la ecuación\ ref {eq:12.2.3}, dividimos por\(T\) para obtener
\[\label{eq:12.2.5} {\tan\theta_2-\tan\theta_1\over\Delta x}= {\rho\over T}u_{tt}(\overline x,t).\]
Dado que\(\tan\theta_1=u_x(x,t)\) y\(\tan\theta_2=u_x(x+\Delta x,t)\), la ecuación\ ref {eq:12.2.5} es equivalente a
\[{u_x(x+\Delta x)-u_x(x,t)\over \Delta x}= {\rho\over T}u_{tt}(\overline x,t).\nonumber\]
Dejar\(\Delta x\to 0\) rendimientos
\[u_{xx}(x,t)={\rho\over T}u_{tt}(x,t),\nonumber\]
que reescribimos como\(u_{tt}=a^2u_{xx}\), con\(a^2=T/\rho\).
La solución formal
Al igual que en la Sección 12.1, utilizamos la separación de variables para obtener una definición adecuada para la solución formal de la Ecuación\ ref {eq:12.2.1}. Comenzamos por buscar funciones de la forma\(v(x,t)=X(x)T(t)\) que no sean idénticamente cero y satisfagan
\[v_{tt}=a^2v_{xx},\quad v(0,t)=0,\quad v(L,t)=0\nonumber\]
para todos\((x,t)\). Desde
\[v_{tt}=XT''\quad \text{and} \quad v_{xx}=X''T,\nonumber\]
\(v_{tt}=a^2v_{xx}\)si y solo si
\[XT''=a^2X''T,\nonumber\]
que reescribimos como
\[{T''\over a^2T}={X''\over X}.\nonumber\]
Para que esto se mantenga para todos\((x,t)\), las dos partes deben igualar la misma constante; así,
\[{X''\over X}={T''\over a^2T}=-\lambda,\nonumber\]
que es equivalente a
\[X''+\lambda X=0\nonumber\]
y
\[\label{eq:12.2.6} T''+a^2\lambda T=0.\]
Desde\(v(0,t)=X(0)T(t)=0\)\(v(L,t)=X(L)T(t)=0\) y y no queremos\(T\) ser idénticamente cero,\(X(0)=0\) y\(X(L)=0\). Por lo tanto,\(\lambda\) debe ser un valor propio de
\[\label{eq:12.2.7} X''+\lambda X=0,\quad X(0)=0,\quad X(L)=0,\]
y\(X\) debe ser una\(\lambda\) -función propia. Del Teorema 11.1.2, los valores propios de la Ecuación\ ref {eq:12.2.7} son\(\lambda_n=n^2\pi^2/L^2\), con funciones propias asociadas
\[X_n=\sin{n\pi x\over L}, \quad n=1,2,3,\dots.\nonumber\]
Sustituyendo\(\lambda=n^2\pi^2/L^2\) en Ecuación\ ref {eq:12.2.6} rendimientos
\[T''+(n^2\pi^2a^2/L^2)T=0,\nonumber\]
que tiene la solución general
\[T_n=\alpha_n\cos{n\pi at\over L}+{\beta_nL\over n\pi a}\sin{n\pi at\over L},\nonumber\]
donde\(\alpha_n\) y\(\beta_n\) son constantes. Ahora vamos
\[v_n(x,t)=X_n(x)T_n(t)=\left(\alpha_n\cos{n\pi at\over L}+ {\beta_nL\over n\pi a}\sin{n\pi at\over L}\right) \sin{n\pi x\over L}.\nonumber\]
Entonces
\[{\partial v_n\over\partial t}(x,t)= \left(-{n\pi a \over L}\alpha_n\sin{n\pi at\over L} +\beta_n\cos{n\pi at\over L}\right)\sin{n\pi x\over L},\nonumber\]
entonces
\[v_n(x,0)=\alpha_n\sin{n\pi x\over L} \quad \text{and} \quad {\partial v_n\over\partial t}(x,0)=\beta_n \sin{n\pi x\over L}.\nonumber\]
Por lo tanto\(v_n\) satisface la Ecuación\ ref {eq:12.2.1} con\(f(x)=\alpha_n \sin n\pi x/L\) y\(g(x)=\beta_n\cos n\pi x/L\). De manera más general\(\alpha_1\), si\(\alpha_2\),,...\(\beta_1\),\(\alpha_m\) y\(\beta_2\),,...,\(\beta_m\) son constantes y
\[u_m(x,t)=\sum_{n=1}^m\left(\alpha_n\cos{n\pi at\over L}+{\beta_nL\over n\pi a}\sin{n\pi at\over L}\right) \sin{n\pi x\over L},\nonumber\]
entonces\(u_m\) satisface la Ecuación\ ref {eq:12.2.1} con
\[f(x)=\sum_{n=1}^m \alpha_n\sin{n\pi x\over L} \quad \text{and} \quad g(x)=\sum_{n=1}^m \beta_n\sin{n\pi x\over L}.\nonumber\]
Esto motiva la siguiente definición.
Si\(f\) y\(g\) son poco uniformes de\([0,L]\), entonces la solución formal de la Ecuación\ ref {eq:12.2.1} es
\[\label{eq:12.2.8} u(x,t)=\sum_{n=1}^\infty\left(\alpha_n\cos{n\pi at\over L}+{\beta_nL\over n\pi a}\sin{n\pi at\over L}\right) \sin{n\pi x\over L},\]
donde
\[S_f(x)=\sum_{n=1}^\infty \alpha_n\sin{n\pi x\over L} \quad \text{and} \quad S_{g}(x)=\sum_{n=1}^\infty \beta_n\sin{n\pi x\over L} \nonumber\]
son las series sinusoidales de Fourier de\(f\) y\(g\) on\([0,L]\); es decir,
\[\alpha_n={2\over L}\int_0^Lf(x)\sin{n\pi x\over L}\,dx \quad \text{and} \quad \beta_n={2\over L}\int_0^Lg(x)\sin{n\pi x\over L}\,dx. \nonumber\]
Como no hay factores productores de convergencia en la Ecuación\ ref {eq:12.2.8} como los exponenciales negativos en\(t\) que aparecen en soluciones formales de problemas de valor de límite inicial para la ecuación de calor, no es obvio que la Ecuación\ ref {eq:12.2.8} incluso converja para cualquier valor de\(x\) y \(t\), y mucho menos que pueda diferenciarse término por término para demostrarlo\(u_{tt}=a^2u_{xx}\). No obstante, el siguiente teorema garantiza que la serie converge no sólo para\(0\le x\le L\) y\(t\ge0\), sino para\(-\infty <x<\infty \) y\(-\infty <t<\infty \).
Si\(f\) y\(g\) son suaves por partes\([0,L]\), entonces\(u\) en Ecuación\ ref {eq:12.2.1} converge para todos\((x,t),\) y se puede escribir como
\[\label{eq:12.2.9} u(x,t)={1\over2}[S_f(x+at)+S_f(x-at)]+ {1\over2a}\int_{x-at}^{x+at}S_g(\tau)\,d\tau.\]
- Prueba
-
Configuración\(A=n\pi x/L\) y\(B=n\pi at/L\) en las identidades
\[\sin A\cos B=\phantom{-}{1\over2}[\sin(A+B)+\sin(A-B)]\nonumber\]
y
\[\sin A\sin B=-{1\over2}[\cos(A+B)-\cos(A-B)]\nonumber\]
rendimientos
\[\label{eq:12.2.10} \cos{n\pi at\over L}\sin{n\pi x\over L} ={1\over2}\left[\sin{n\pi(x+at)\over L}+\sin{n\pi(x-at)\over L}\right]\]
y
\[\label{eq:12.2.11} \begin{array}{ccl} {\sin \frac{n \pi a t}{L} \sin \frac{n \pi x}{L} }&{=}&{-\frac{1}{2}\left[\cos \frac{n \pi(x+a t)}{L}-\cos \frac{n \pi(x-a t)}{L}\right]} \\{} &{=}&{\frac{n \pi}{2 L} \int_{x-a t}^{x+a t} \sin \frac{n \pi \tau}{L} d \tau} \end{array}\]
De la ecuación\ ref {eq:12.2.10},
\[\label{eq:12.2.12} \begin{array}{ccl} {\sum_{n=1}^{\infty} \alpha_{n} \cos \frac{n \pi a t}{L} \sin \frac{n \pi x}{L}} &{=}&{\frac{1}{2} \sum_{n=1}^{\infty} \alpha_{n}\left(\sin \frac{n \pi(x+a t)}{L}+\sin \frac{n \pi(x-a t)}{L}\right)} \\{} &{=}&{\frac{1}{2}\left[S_{f}(x+a t)+S_{f}(x-a t)\right]} \end{array}\]
Dado que se puede demostrar que una serie sinusoidal de Fourier puede integrarse término por término entre dos límites cualesquiera, la Ecuación\ ref {eq:12.2.11} implica que
\[\begin{aligned} \sum_{n=1}^{\infty} \frac{\beta_{n} L}{n \pi a} \sin \frac{n \pi a t}{L} \sin \frac{n \pi x}{L} &=\frac{1}{2 a} \sum_{n=1}^{\infty} \beta_{n} \int_{x-a t}^{x+a t} \sin \frac{n \pi \tau}{L} d \tau \\ &=\frac{1}{2 a} \int_{x-a t}^{x+a t}\left(\sum_{n=1}^{\infty} \beta_{n} \sin \frac{n \pi \tau}{L}\right) d \tau \\ &=\frac{1}{2 a} \int_{x-a t}^{x+a t} S_{g}(\tau) d \tau \end{aligned}\nonumber \]
Esto y la Ecuación\ ref {eq:12.2.12} implican la Ecuación\ ref {eq:12.2.9}, que completa la prueba.
Como veremos a continuación, si\(S_g\) es diferenciable y\(S_f\) es dos veces diferenciable en\((-\infty,\infty)\), entonces la Ecuación\ ref {eq:12.2.9} satisface\(u_{tt}=a^2u_{xx}\) para todos\((x,t)\). Necesitamos el siguiente teorema para formular condiciones sobre\(f\) y\(g\) tal que\(S_f\) y\(S_g\) para tener estas propiedades.
Supongamos que\(h\) es diferenciable en\([0,L]\); es decir,\(h'(x)\) existe para\(0<x<L\), y las derivadas unilaterales existen\[h'_+(0)=\lim_{x\to0+}{h(x)-h(0)\over x} \quad \text{and} \quad h'_-(L)=\lim_{x\to L-}{h(x)-h(L)\over x-L}\nonumber\] ambas.
- (a) Dejar\(p\) ser la extensión periódica impar de\(h\) a\((-\infty,\infty);\) eso es,\[p(x)=\left\{\begin{array}{cc} {h(x),}&{0\leq x\leq L,}\\{-h(-x),}&{-L<x<0,}\end{array} \right. \quad and\: p(x+2L)=p(x),\quad -\infty <x<\infty. \nonumber\] Entonces\(p\) es diferenciable en\((-\infty , \infty )\) si y sólo si\[\label{eq:12.2.13} h(0)=h(L)=0\]
- Que\(q\) sea la extensión periódica uniforme de\(h\) a\((-\infty,\infty);\) eso es,\[p(x)=\left\{\begin{array}{cc}{h(x),}&{0\leq x\leq L,}\\{h(-x),}&{-L<x<0,}\end{array} \right. \quad and\: q(x+2L)=q(x),\quad -\infty <x<\infty. \nonumber\] Entonces\(pq\) es diferenciable sobre\((-\infty , \infty )\) si y solo si\[\label{eq:12.2.14} h_{+}^{\prime}(0)=h_{-}^{\prime}(L)=0\]
- Prueba
-
A lo largo de esta prueba,\(k\) denota un entero. Ya que\(f\) es diferenciable en el intervalo abierto\((0,L)\), ambos\(p\) y\(q\) son diferenciables en cada intervalo abierto\(((k-1)L,kL)\). Por lo tanto, sólo necesitamos determinar si\(p\) y\(q\) son diferenciables en\(x=kL\) para cada uno\(k\).
(a) De la Figura 12.2.3 ,\(p\) es discontinuo en\(x=2kL\) if\(h(0)\ne0\) y discontinuo en\(x=(2k-1)L\) if\(h(L)\ne0\). Por lo tanto no\(p\) es diferenciable a\((-\infty,\infty)\) menos que\(h(0)=h(L)=0\). De la Figura 12.2.4 , si\(h(0)=h(L)=0\), entonces
\[p'(2kL)=h_+'(0)\quad \text{and} \quad p'((2k-1)L)=h_-'(L)\nonumber\]
para cada\(k\); por lo tanto,\(p\) es diferenciable en\((-\infty,\infty)\).
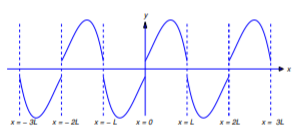
Figura 12.2.3 : La extensión impar de una función que no satisface\ ref {eq:12.2.13} 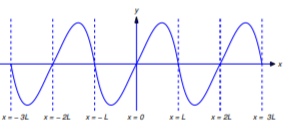
Figura 12.2.4 : La extensión impar de una función que satisface\ ref {eq:12.2.13} (b) De la Figura 12.2.5 ,
\[q'_-(2kL)=-h'_+(0)\quad \text{and} \quad q'_+(2kL)=h'_+(0),\nonumber\]
así\(q\) es diferenciable en\(x=2kL\) si y solo si\(h'_+(0)=0\). También,
\[q'_-((2k-1)L)=h'_-(L) \quad \text{and} \quad q'_+((2k-1)L)= -h'_-(L) ,\nonumber\]
así\(q\) es diferenciable en\(x=(2k-1)L\) si y solo si\(h'_-(L)=0\). Por lo tanto\(q\) es diferenciable en\((-\infty,\infty)\) si y solo si\(h'_{+}(0)=h'_\: (L)=0\), como en la Figura 12.2.6 . Esto completa la prueba.
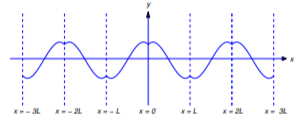
Figura 12.2.5 : La extensión par de una función que no satisface\ ref {eq:12.2.14} 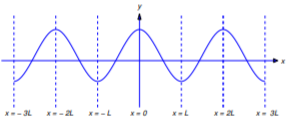
Figura 12.2.6 : La extensión par de una función que satisface\ ref {eq:12.2.14}
La solución formal de\(\eqref{eq:12.2.1}\) es una solución real si\(g\) es diferenciable en\([0,L]\) y
\[\label{eq:12.2.15} g(0)=g(L)=0,\]
mientras que\(f\) es dos veces diferenciable en\([0,L]\) y
\[\label{eq:12.2.16} f(0)=f(L)=0\]
y
\[\label{eq:12.2.17} f''_+(0)=f''_-(L)=0.\]
- Prueba
-
Primero mostramos que\(S_g\) es diferenciable y\(S_f\) es dos veces diferenciable en\((-\infty,\infty)\). Luego diferenciaremos la Ecuación\ ref {eq:12.2.9} dos veces con respecto a\(x\)\(t\) y verificaremos que la Ecuación\ ref {eq:12.2.9} es una solución real de la Ecuación\ ref {eq:12.2.1}.
Ya que\(f\) y\(g\) son continuos en\((0,L)\), el Teorema 11.3.2 implica que\(S_f(x)=f(x)\) y\(S_g(x)=g(x)\) en\([0,L]\). Por lo tanto\(S_f\) y\(S_g\) son las extensiones periódicas impares de\(f\) y\(g\). Dado que\(f\) y\(g\) son diferenciables en\([0,L]\), Ecuación\ ref {eq:12.2.15}, Ecuación\ ref {eq:12.2.16}, y Teorema 12.2.3 a implican que\(S_f\) y\(S_g\) son diferenciables en\((-\infty,\infty)\).
Dado que\(S_f'(x)=f'(x)\) on\([0,L]\) (derivadas unilaterales en los puntos finales), y\(S_f'\) es par (la derivada de una función impar es par),\(S_f'\) es la extensión periódica par de\(f'\). Por supuesto,\(f'\) es diferenciable en\([0,L]\). Debido a la Ecuación\ ref {eq:12.2.17}, Teorema 12.2.3 b con\(h=f'\) e\(q=S_f'\) implica que\(S_f''\) existe en\((-\infty,\infty)\).
Ahora podemos diferenciar la Ecuación\ ref {eq:12.2.9} dos veces con respecto a\(x\) y\(t\):
\[u_x(x,t)={1\over2}[S_f'(x+at)+S_f'(x-at)]+ {1\over2a}[S_g(x+at)-S_g(x-at)],\nonumber\]
\[\label{eq:12.2.18} u_{xx}(x,t)={1\over2}[S_f''(x+at)+S_f''(x-at)]+ {1\over2a}[S_g'(x+at)-S_g'(x-at)],\]
\[\label{eq:12.2.19} u_t(x,t)={a\over2}[S_f'(x+at)-S_f'(x-at)]+ {1\over2}[S_g(x+at)+S_g(x-at)],\]
y
\[\label{eq:12.2.20} u_{tt}(x,t)={a^2\over2}[S_f''(x+at)-S_f''(x-at)]+ {a\over2}[S_g'(x+at)-S_g'(x-at)].\]
Comparando la Ecuación\ ref {eq:12.2.18} y la Ecuación\ ref {eq:12.2.20} muestra eso\(u_{tt}(x,t)=a^2u_{xx}(x,t)\) para todos\((x,t)\).
De la Ecuación\ ref {eq:12.2.8},\(u(0,t)=u(L,t)=0\) para todos\(t\). De la Ecuación\ ref {eq:12.2.9},\(u(x,0)=S_f(x)\) para todos\(x\), y por lo tanto, en particular,
\[u(x,0)=f(x),\quad 0\le x< L.\nonumber\]
De la Ecuación\ ref {eq:12.2.19},\(u_t(x,0)=S_g(x)\) para todos\(x\), y por lo tanto, en particular,
\[u_t(x,0)=g(x),\quad 0\le x< L.\nonumber\]
Por lo tanto\(u\) es una solución real de la Ecuación\ ref {eq:12.2.1}. Esto completa la prueba.
La ecuación\ ref {eq:12.2.9} se llama la solución de D'Alembert de la ecuación\ ref {eq:12.2.1}. Aunque la solución de D'alembert fue útil para probar el teorema 12.2.4
y es muy útil en un contexto ligeramente diferente (Ejercicios 12.2.63 - 12.2.68), la Ecuación\ ref {eq:12.2.8} es preferible para fines computacionales.
Resolver Ecuación\ ref {eq:12.2.1} con
\[f(x)=x(x^3-2Lx^2+L^2) \quad \text{and} \quad g(x)=x(L-x).\nonumber \]
Solución
Te dejamos a ti verificar eso\(f\) y\(g\) satisfacer los supuestos del Teorema 12.2.4 .
Del Ejercicio 11.3.39,
\[S_f(x)={96L^4\over\pi^5}\sum_{n=1}^\infty{1\over(2n-1)^5}\sin{(2n-1)\pi x\over L}.\nonumber\]
Del Ejercicio 11.3.36,
\[S_g(x)={8L^2\over\pi^3}\sum_{n=1}^\infty{1\over(2n-1)^3}\sin{(2n-1)\pi x\over L}.\nonumber\]
De la ecuación\ ref {eq:12.2.8},
\[\begin{aligned} u(x, t)=& \frac{96 L^{4}}{\pi^{5}} \sum_{n=1}^{\infty} \frac{1}{(2 n-1)^{5}} \cos \frac{(2 n-1) \pi a t}{L} \sin \frac{(2 n-1) \pi x}{L} \\ &+\frac{8 L^{3}}{a \pi^{4}} \sum_{n=1}^{\infty} \frac{1}{(2 n-1)^{4}} \sin \frac{(2 n-1) \pi a t}{L} \sin \frac{(2 n-1) \pi x}{L} \end{aligned}\nonumber \]
El teorema 12.1.2 implica que\(u_{xx}\) y se\(u_{tt}\) puede obtener por término a término la diferenciación, para todos\((x,t)\), así\(u_{tt}=a^2u_{xx}\) para todos\((x,t)\) (Ejercicio 12.2.62). Además, el Teorema 11.3.2 implica que\(S_f(x)=f(x)\) y\(S_g(x)=g(x)\) si\(0\le x\le L\). Por lo tanto\(u(x,0)=f(x)\) y\(u_t(x,0)=g(x)\) si\(0\le x\le L\). Por lo tanto,\(u\) es una solución real del problema del valor de límite inicial.
Al resolver un problema específico de valor de límite inicial (Ecuación\ ref {eq:12.2.1}), es conveniente resolver el problema con\(g \equiv 0\), luego con\(f \equiv 0\), y agregar las soluciones para obtener la solución del problema dado. Debido a esto, ya sea\(f \equiv 0\) o\(g \equiv 0\) en todos los problemas específicos de valor inicial-límite en los ejercicios.
La cuerda arrancada
Si\(f\) y\(g\) no satisfacen los supuestos del Teorema 12.2.4 , entonces la Ecuación\ ref {eq:12.2.8} no es una solución real de la Ecuación\ ref {eq:12.2.1} de hecho, se puede demostrar que la Ecuación\ ref {eq:12.2.1} no tiene una solución real en este caso. Sin embargo,\(u\) se define para todos\((x,t)\), y podemos ver a partir de la Ecuación\ ref {eq:12.2.18} y la Ecuación\ ref {eq:12.2.20} que\(u_{tt}(x,t)=a^2u_{xx}(x,t)\) para todos\((x,t)\) tales que\(S_f''(x\pm at)\) y\(S_g'(x\pm at)\) existen. Además, aún\(u\) puede proporcionar una aproximación útil a la vibración de la cuerda; un experimento de laboratorio puede confirmarlo o negarlo.
Ahora consideraremos el problema del valor de límite inicial Ecuación\ ref {eq:12.2.1} con
\[\label{eq:12.2.21} f(x)= \left\{\begin{array}{cl} x,&0\le x\le{L\over2},\\L-x,&{L\over2}\le x\le L \end{array}\right.\]
y\(g\equiv0\). Dado que no\(f\) es diferenciable en\(x=L/2\), no satisface los supuestos del Teorema 12.2.4 , por lo que la solución formal de la Ecuación\ ref {eq:12.2.1} no puede ser una solución real. Sin embargo, es instructivo investigar las propiedades de la solución formal.
El gráfico de\(f\) se muestra en la Figura 12.2.7 . Intuitivamente, estamos arrancando la cuerda por la mitad de su longitud en el centro. Tienes razón si crees que se trata de un desplazamiento extraordinariamente grande; sin embargo, podríamos eliminar esta objeción multiplicando la función en la Figura 12.2.7 por una pequeña constante. Como esto simplemente multiplicaría la solución formal por la misma constante, saldremos\(f\) como la hemos definido. Comentarios similares se aplican a los ejercicios.
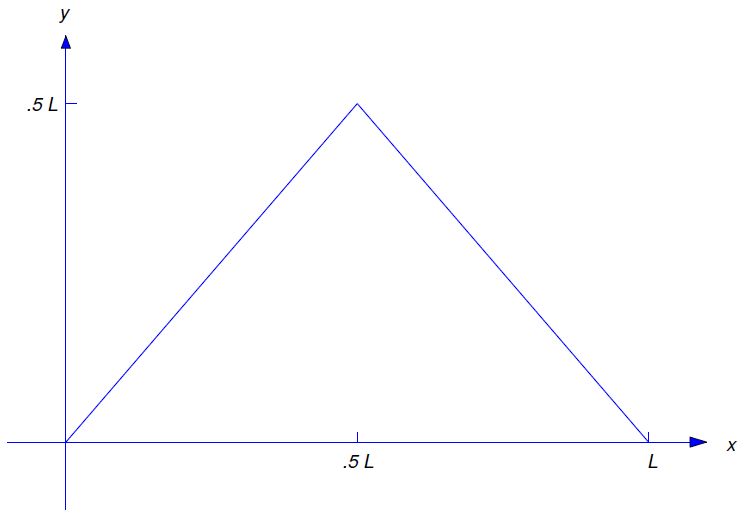
Del Ejercicio 11.3.15, la serie sinusoidal de Fourier de\(f\) on\([0,L]\) es
\[S_{f}(x)=\frac{4 L}{\pi^{2}} \sum_{n=1}^{\infty} \frac{(-1)^{n+1}}{(2 n-1)^{2}} \sin \frac{(2 n-1) \pi x}{L}\nonumber\]
que converge a\(f\) para todos\(x\) en\([0,L]\), por Teorema 11.3.2. Por lo tanto
\[\label{eq:12.2.22} u(x, t)=\frac{4 L}{\pi^{2}} \sum_{n=1}^{\infty} \frac{(-1)^{n+1}}{(2 n-1)^{2}} \cos \frac{(2 n-1) \pi a t}{L} \sin \frac{(2 n-1) \pi x}{L}\]
Esta serie converge absolutamente para todos\((x,t)\) por la prueba de comparación, ya que la serie
\[\sum_{n=1}^\infty{1\over(2n-1)^2}\nonumber\]
converge. Además, la ecuación\ ref {eq:12.2.22} satisface las condiciones de límite
\[u(0,t)=u(L,t)=0,\quad t>0,\nonumber\]
y la condición inicial
\[u(x,0)=f(x),\quad 0\le x\le L.\nonumber\]
Sin embargo, no podemos justificar diferenciar Ecuación\ ref {eq:12.2.22} término por término ni siquiera una vez, y diferenciarlo formalmente dos veces término por término produce una serie que diverge para todos\((x,t)\). (Verificar.). Por lo tanto utilizamos la forma de d'Alembert
\[\label{eq:12.2.23} u(x,t)={1\over2}[S_f(x+at)+S_f(x-at)]\]
para\(u\) estudiar sus derivados. La figura 12.2.8 muestra la gráfica de\(S_f\), que es la extensión periódica impar de\(f\). Se puede ver en la gráfica que\(S_f\) es diferenciable en\(x\) (y\(S_f'(x)=\pm1\)) si y solo si no\(x\) es un múltiplo impar de\(L/2\).
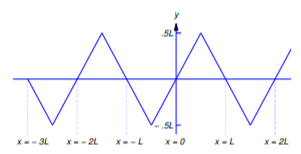
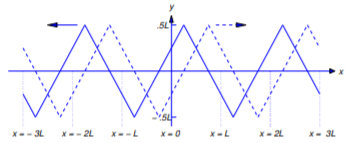
En la Figura 12.2.9 las curvas discontinuas y sólidas son las gráficas de\(y=S_f(x-at)\) y\(y=S_f(x+at)\) respectivamente, para un valor fijo de\(t\). A\(t\) medida que aumenta la curva discontinua se mueve hacia la derecha y la curva sólida se mueve hacia la izquierda. Por ello, decimos que las funciones\(u_1(x,t)=S_f(x+at)\) y\(u_2(x,t)=S_f(x-at)\) son olas viajeras. Tenga en cuenta que\(u_1\) satisface la ecuación de onda en\((x,t)\) si no\(x+at\) es un múltiplo impar de\(L/2\) y\(u_2\) satisface la ecuación de onda en\((x,t)\) si no\(x-at\) es un múltiplo impar de\(L/2\). Por lo tanto, la Ecuación\ ref {eq:12.2.23} (o, equivalentemente, la Ecuación\ ref {eq:12.2.22}) satisface\(u_{tt}(x,t)=a^2u_{xx}(x,t)=0\) para todos\((x,t)\) tales que\(x-at\) ni ni\(x+at\) es un múltiplo impar de\(L/2\).
Concluimos encontrando una fórmula explícita para\(u(x,t)\) bajo el supuesto de que
\[\label{eq:12.2.24} 0\le x\le L\quad \text{and} \quad 0\le t\le L/2a.\]
Para ver cómo se puede usar esta fórmula para calcular\(u(x,t)\) para\(0\le x\le L\) y arbitraria\(t\), le remitimos al Ejercicio 12.2.16.
De la Figura 12.2.10 ,
\[S_f(x-at)= \left\{\begin{array}{cl} x-at,&0\le x\le {L\over2}+at,\\[4pt] L-x+at,&{L\over2}+at\le x\le L \end{array}\right.\nonumber\]
y
\[S_f(x+at)= \left\{\begin{array}{cl} x+at,&0\le x\le {L\over2}-at,\\[4pt] L-x-at,&{L\over2}-at\le x\le L \end{array}\right.\nonumber\]
si\((x,t)\) cumple Ecuación\ ref {eq:12.2.24}.
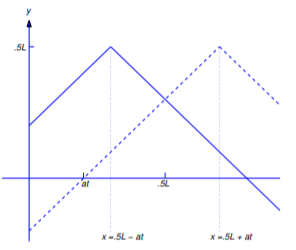
Por lo tanto, a partir de la Ecuación\ ref {eq:12.2.23},
\[u(x,t)= \left\{\begin{array}{cl} x,&0\le x\le{L\over2}-at,\\[4pt] {L\over2}-at,&{L\over2}-at\le x\le{L\over2}+at,\\[4pt] L-x,&{L\over2}-at\le x\le L \end{array}\right.\nonumber\]
si\((x,t)\) cumple Ecuación\ ref {eq:12.2.24}. La figura 12.2.11 es la gráfica de esta función encendida\([0,L]\) para una entrada fija\(t\)\((0,L/2a)\).
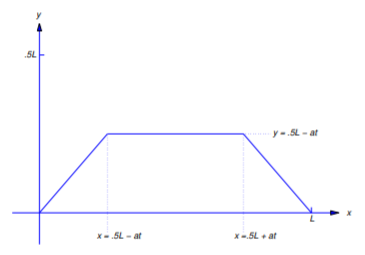
Uso de la tecnología
Aunque la solución formal
\[u(x,t)=\sum_{n=1}^\infty\left(\alpha_n\cos{n\pi at\over L}+{\beta_nL\over n\pi a}\sin{n\pi at\over L}\right) \sin{n\pi x\over L}\nonumber\]
de Ecuación\ ref {eq:12.2.1} se define para todos\((x,t)\), nos interesa principalmente su comportamiento para\(0\le x\le L\) y\(t\ge0\). De hecho, basta con considerar solo valores de\(t\) en el intervalo\(0\le t<2L/a\), ya que
\[u(x,t+2kL/a)=u(x,t)\nonumber\]
para todos\((x,t)\) si\(k\) es un entero. (Verificar.)
Puede crear una animación del movimiento de la cuerda realizando el siguiente experimento numérico.
Dejar\(m\) y\(k\) ser enteros positivos. Let
\[t_j={2Lj\over ka},\quad j=0,1,\dots k;\nonumber\]
así,\(t_0\),\(t_1\),...\(t_k\) son puntos igualmente espaciados en\([0,2L/a]\). Para cada\(j=0\),\(1\),\(2\),...\(k\), graficar la suma parcial
\[u_m(x,t_j)=\sum_{n=1}^m\left(\alpha_n\cos{n\pi at_j\over L}+{\beta_nL\over n\pi a}\sin{n\pi at_j\over L}\right) \sin{n\pi x\over L}\nonumber\]
\([0,L]\)en función de\(x\). Escribe tu programa para que cada gráfico permanezca visualizado en el monitor por un corto tiempo, y luego sea eliminado y reemplazado por el siguiente. Repita este procedimiento para diversos valores de\(m\) y\(k\).


