12.4: Ecuación de Laplace en Coordenadas Polares
- Page ID
- 114792
En la Sección 12.3 resolvimos problemas de valor límite para la ecuación de Laplace sobre un rectángulo con lados paralelos a los\(x,y\) ejes. Ahora consideraremos problemas de valor límite para la ecuación de Laplace sobre regiones con límites mejor descritos en términos de coordenadas polares. En este caso es apropiado considerar\(u\) como función\((r,\theta)\) y escribir la ecuación de Laplace en forma polar como
\[\label{eq:12.4.1} u_{rr}+\frac{1}{r}u_r+\frac{1}{r^2}u_{\theta\theta}=0,\]
donde
\[r=\sqrt{x^2+y^2}\quad \text{and} \quad \theta=\cos^{-1}\frac{x}{r}=\sin^{-1}\frac{x}{r}. \nonumber\]
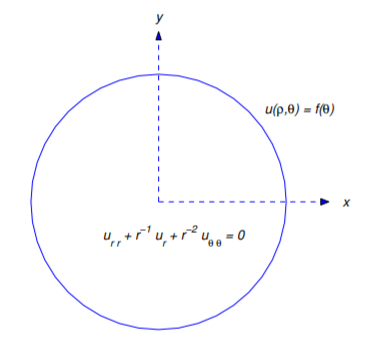
Comenzamos con el caso donde la región es un disco circular con radio\(\rho\), centrado en el origen; es decir, queremos definir una solución formal del problema del valor límite
\[\label{eq:12.4.2} \begin{array}{c}{u_{rr}+\frac{1}{r}u_{r}+\frac{1}{r^{2}}u_{\theta \theta}=0,\quad 0<r<\rho ,\quad -\pi \leq \theta <\pi ,}\\{u(\rho ,\theta )=f(\theta ),\quad -\pi\leq\theta <\pi }\end{array}\]
(Figura 12.4.1 ). Tenga en cuenta que la Ecuación\ ref {eq:12.4.2} no impone ninguna restricción sobre\(u(r,\theta)\) cuándo\(r=0\). Abordaremos esta pregunta en el momento apropiado.
Primero buscamos productos\(v(r,\theta)=R(r)\Theta(\theta)\) que satisfagan la Ecuación\ ref {eq:12.4.1}. Para esta función,
\[v_{rr}+\frac{1}{r}v_r+\frac{1}{r^2}v_{\theta\theta}= R''\Theta+\frac{1}{r}R'\Theta +\frac{1}{r^2}R\Theta''= 0 \nonumber\]
para todos\((r,\theta)\) con\(r\ne0\) si
\[\frac{r^2R''+rR'}{R}=-\frac{\Theta''}{\Theta}=\lambda, \nonumber\]
donde\(\lambda\) es una constante de separación. (Verificar.) Esta ecuación es equivalente a
\[\Theta''+\lambda\Theta=0 \nonumber\]
y
\[\label{eq:12.4.3} r^2R''+rR'-\lambda R=0.\]
Dado que\((r,\pi)\) y\((r,-\pi)\) son las coordenadas polares del mismo punto, imponemos condiciones de frontera periódicas sobre\(\Theta\); es decir,
\[\label{eq:12.4.4} \Theta''+\lambda\Theta=0,\quad \Theta(-\pi)=\Theta(\pi), \quad \Theta'(-\pi)=\Theta'(\pi).\]
Ya que no\(R\Theta\) queremos ser idénticamente cero,\(\lambda\) debe ser un valor propio de la Ecuación\ ref {eq:12.4.4} y\(\Theta\) debe ser una función propia asociada. Del Teorema 11.1.6, los valores propios de la Ecuación\ ref {eq:12.4.4} son\(\lambda_0=0\) con funciones propias asociadas\(\Theta_0=1\) y, for\(n=1,2,3,\dots,\)\(\lambda_n=n^2\), con función propia asociada\(\cos n\theta\) y\(\sin n\theta\) por lo tanto,
\[\Theta_n=\alpha_n\cos n\theta+\beta_n\sin n\theta \nonumber\]
donde\(\alpha_n\) y\(\beta_n\) son constantes.
Sustituir\(\lambda=0\) en la ecuación\ ref {eq:12.4.3} produce el
\[r^2R''+rR'=0,\nonumber\]
por lo
\[\frac{R_0''}{R_0'}=-\frac{1}{r},\nonumber\]
\[R_0'=\frac{c_1}{r},\nonumber\]
y
\[\label{eq:12.4.5} R_0=c_2+c_1\ln r.\]
Si\(c_1\ne0\) entonces
\[\lim_{r\to0+}|R_0(r)|=\infty,\nonumber\]
lo cual no tiene sentido si interpretamos\(u_0(r,\theta)=R_0(r)\Theta_0(\theta)=R_0(r)\) como la distribución de temperatura de estado estacionario en un disco cuyo límite se mantiene a la temperatura constante\(R_0(\rho)\). Por lo tanto ahora\(R_0\) requerimos estar acotados como\(r\to0+\). Esto implica eso\(c_1=0\), y tomamos\(c_2=1\). Así,\(R_0=1\) y\(v_0(r,\theta)=R_0(r)\Theta_0(\theta)=1\). Tenga en cuenta que\(v_0\) satisface la Ecuación\ ref {eq:12.4.2} con\(f(\theta)=1\).
Sustituir\(\lambda=n^2\) en la ecuación\ ref {eq:12.4.3} produce la ecuación de Euler
\[\label{eq:12.4.6} r^2R_n''+rR_n'-n^2 R_n=0\]
para\(R_n\). El polinomio indicial de esta ecuación es
\[s(s-1)+s-n^2=(s-n)(s+n),\nonumber\]
así que la solución general de la Ecuación\ ref {eq:12.4.6} es
\[\label{eq:12.4.7} R_n=c_1r^n+c_2r^{-n},\]
por Teorema 7.4.3. Consistente con nuestra suposición anterior sobre\(R_0\), ahora requerimos\(R_n\) estar delimitados como\(r\to0+\). Esto implica eso\(c_2=0\), y nosotros elegimos\(c_1=\rho^{-n}\). Entonces\(R_n(r)=r^n/\rho^n\), entonces
\[v_n(r,\theta)=R_n(r)\Theta_n(\theta)=\frac{r^n}{\rho^n}(\alpha_n\cos n\theta+\beta_n\sin n\theta).\nonumber\]
Ahora\(v_n\) satisface la Ecuación\ ref {eq:12.4.2} con
\[f(\theta)=\alpha_n\cos n\theta+\beta_n\sin n\theta.\nonumber\]
De manera más general\(\alpha_0\), si\(\alpha_1\),,...,\(\alpha_m\) y\(\beta_1\)\(\beta_2\),,...,\(\beta_m\) son constantes arbitrarias entonces
\[u_m(r,\theta)=\alpha_0+\sum_{n=1}^m\frac{r^n}{\rho^n}(\alpha_n\cos n\theta+\beta_n\sin n\theta)\nonumber\]
satisface la Ecuación\ ref {eq:12.4.2} con
\[f(\theta) =\alpha_0+\sum_{n=1}^m(\alpha_n\cos n\theta+\beta_n\sin n\theta).\nonumber\]
Esto motiva la siguiente definición.
La solución formal acotada del problema del valor límite Ecuación\ ref {eq:12.4.2} es
\[\label{eq:12.4.8} u(r,\theta)=\alpha_0+\sum_{n=1}^\infty\frac{r^n}{\rho^n}(\alpha_n\cos n\theta+\beta_n\sin n\theta),\]
donde
\[F(\theta) =\alpha_0+\sum_{n=1}^\infty(\alpha_n\cos n\theta+\beta_n\sin n\theta)\nonumber\]
es la serie de Fourier de\(f\) on\([-\pi,\pi]\); es decir,
\[\alpha_0=\frac{1}{2\pi}\int_{-\pi}^\pi f(\theta)\,d\theta,\nonumber\]
y
\[\alpha_n=\frac{1}{\pi}\int_{-\pi}^\pi f(\theta)\cos n\theta\,d\theta \quad \text{and} \quad \beta_n=\frac{1}{\pi}\int_{-\pi}^\pi f(\theta)\sin n\theta\,d\theta, \quad n=1,2,3,\dots.\nonumber\]
Ya que\(\sum_{n=0}^\infty n^k(r/\rho)^n\) converge para cada\(k\) si\(0< r<\rho\), el Teorema 12.1.2 se puede utilizar para mostrar que si\(0< r<\rho\) entonces la Ecuación\ ref {eq:12.4.8} se puede diferenciar término por término cualquier número de veces con respecto a ambos\(r\) y\(\theta\). Dado que los términos en la Ecuación\ ref {eq:12.4.8} satisfacen la ecuación de Laplace if\(r>0\), Ecuación\ ref {eq:12.4.8} satisface la ecuación de Laplace si\ (0
\[F(\theta)=f(\theta),\quad -\pi\le\theta<\pi.\nonumber\]
Del Teorema 11.2.4, esto es cierto si\(f\) es continuo y por partes suave en\([-\pi,\pi]\) y\(f(-\pi)=f(\pi)\).
Encuentra la solución formal acotada de la Ecuación\ ref {eq:12.4.2} con\(f(\theta)=\theta(\pi^2-\theta^2)\).
Solución
Del Ejemplo 11.2.6
\[\theta(\pi^2-\theta^2)=12\sum_{n=1}^\infty\frac{(-1)^n}{n^3}\sin n\theta,\quad -\pi\le\theta\le\pi,\nonumber\]
por lo
\[u(r,\theta)=12\sum_{n=1}^\infty\frac{r^n}{\rho^n}\frac{(-1)^n}{n^3}\sin n\theta,\quad 0\le r\le \rho,\quad -\pi\le\theta\le\pi.\nonumber\]
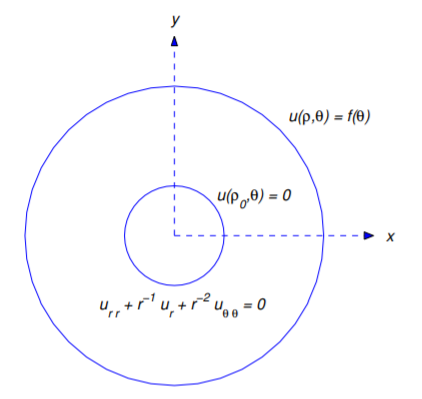
Definir la solución formal de
\[\label{eq:12.4.9} \begin{array}{c}{u_{rr}+\frac{1}{r}u_{r}+\frac{1}{r^{2}}u_{\theta\theta}=0,\quad \rho _{0}<r<\rho ,\quad -\pi \leq\theta <\pi , }\\{u(\rho _{0},\theta )=0,\quad u(\rho, \theta )=f(\theta ),\quad -\pi\leq\theta <\pi ,}\end{array}\]
donde\(0<\rho_0<\rho\) (Figura 12.4.2 ).
Solución
Usamos separación de variables exactamente como antes, excepto que ahora elegimos las constantes en Ecuación\ ref {eq:12.4.5} y Ecuación\ ref {eq:12.4.7}\(R_n(\rho_0)=0\) para que para\(n=0\),\(1\),\(2\),... En vista de la condición de Dirichlet no homogénea en el límite\(r=\rho\), también es conveniente exigir que\(R_n(\rho)=1\) para\(n=0\),\(1\),\(2\),... Te dejamos que verifiques que
\[R_0(r)=\frac{\ln r/\rho_0}{\ln\rho/\rho_0} \quad \text{and} \quad R_n=\frac{\rho_0^{-n}r^n-\rho_0^nr^{-n}} {\rho_0^{-n}\rho^n-\rho_0^n\rho^{-n}},\quad n=1,2,3,\dots\nonumber\]
satisfacer estos requisitos. Por lo tanto
\[v_0(\rho,\theta)=\frac{\ln r/\rho_0}{\ln\rho/\rho_0}\nonumber\]
y
\[v_n(r,\theta)=\frac{\rho_0^{-n}r^n-\rho_0^nr^{-n}} {\rho_0^{-n}\rho^n-\rho_0^n\rho^{-n}}(\alpha_n\cos n\theta+\beta_n\sin n\theta), \quad n=1,2,3,\dots,\nonumber\]
donde\(\alpha_n\) y\(\beta_n\) son constantes arbitrarias.
Si\(\alpha_0\),\(\alpha_1\),...,\(\alpha_m\) y\(\beta_1\),\(\beta_2\),...,\(\beta_m\) son constantes arbitrarias entonces
\[u_m(r,\theta)=\alpha_0\frac{\ln r/\rho_0}{\ln\rho/\rho_0}+ \sum_{n=1}^m \frac{\rho_0^{-n}r^n-\rho_0^nr^{-n}} {\rho_0^{-n}\rho^n-\rho_0^n\rho^{-n}} (\alpha_n\cos n\theta+\beta_n\sin n\theta)\nonumber\]
satisface la Ecuación\ ref {eq:12.4.9}, con
\[f(\theta) =\alpha_0+\sum_{n=1}^m(\alpha_n\cos n\theta+\beta_n\sin n\theta).\nonumber\]
Esto nos motiva a definir la solución formal de la Ecuación\ ref {eq:12.4.9} para\(f\) que sea general
\[u(r,\theta)=\alpha_0\frac{\ln r/\rho_0}{\ln\rho/\rho_0}+ \sum_{n=1}^\infty \frac{\rho_0^{-n}r^n-\rho_0^nr^{-n}} {\rho_0^{-n}\rho^n-\rho_0^n\rho^{-n}} (\alpha_n\cos n\theta+\beta_n\sin n\theta),\nonumber\]
donde
\[F(\theta) =\alpha_0+\sum_{n=1}^\infty(\alpha_n\cos n\theta+\beta_n\sin n\theta)\nonumber\]
es la serie de Fourier de\(f\) on\([-\pi,\pi]\).
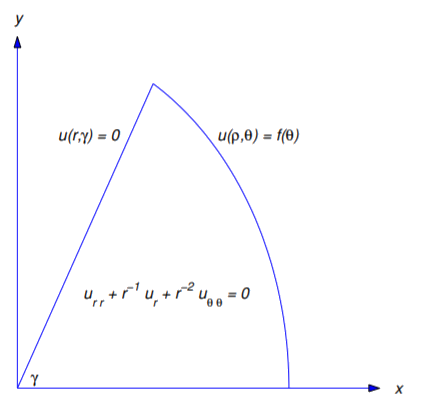
Definir la solución formal acotada de
\[\label{eq:12.4.10} \begin{array}{c}{u_{rr}+\frac{1}{r}u_{r}+\frac{1}{r^{2}}u_{\theta\theta}=0,\quad 0<r<\rho,\quad 0<\theta <\gamma , }\\{u(\rho ,\theta )= f(\theta ),\quad 0\leq \theta\leq\gamma ,}\\ {u(r,0)=0,\quad u(r,\gamma )=0,\quad 0<r<\rho ,} \end{array}\]
donde\(0<\gamma<2\pi\) (Figura 12.4.3 ).
Solución
Ahora\(v(r,\theta)=R(r)\Theta(\theta)\), donde
\[\label{eq:12.4.11} r^2R''+rR'-\lambda R=0\]
y
\[\label{eq:12.4.12} \Theta''+\lambda\Theta=0,\quad \Theta(0)=0,\quad \Theta(\gamma)=0.\]
Del Teorema 11.1.2, los valores propios de la Ecuación\ ref {eq:12.4.12} son\(\lambda_n=n^2\pi^2/\gamma^2\), con función propia asociada\(\Theta_n=\sin n\pi\theta/\gamma\),\(n=1\),\(2\),\(3\),... Sustituir\(\lambda=n^2\pi^2/\gamma^2\) en la ecuación\ ref {eq:12.4.11} produce la ecuación de Euler
\[r^2R''+rR_n'-\frac{n^2\pi^2}{\gamma^2} R=0.\nonumber\]
El polinomio indicial de esta ecuación es
\[s(s-1)+s-\frac{n^2\pi^2}{\gamma^2}=\left(s-\frac{n\pi}{\gamma}\right) \left(s+\frac{n\pi}{\gamma}\right),\nonumber\]
por lo
\[R_n=c_1r^{n\pi/\gamma}+c_2r^{-n\pi/\gamma},\nonumber\]
por Teorema 7.4.3. Para obtener una solución que quede acotada como\(r\to0+\) dejamos\(c_2=0\). Debido a la condición de Dirichlet en\(r=\rho\), es conveniente tener\(r(\rho)=1\); por lo tanto tomamos\(c_1=\rho^{-n\pi/\gamma}\), entonces
\[R_n(r)=\frac{r^{n\pi/\gamma}}{\rho^{n\pi/\gamma}}.\nonumber\]
Ahora
\[v_n(r,\theta)=R_n(r)\Theta_n(\theta)=\frac{r^{n\pi/\gamma}} {\rho^{n\pi/\gamma}}\sin\frac{n\pi\theta}{\gamma}\nonumber\]
satisface la Ecuación\ ref {eq:12.4.10} con
\[f(\theta)=\sin\frac{n\pi\theta}{\gamma}.\nonumber\]
De manera más general\(\alpha_1\), si\(\alpha_2\),,...,\(\alpha_m\) y son constantes arbitrarias entonces
\[u_m(r,\theta)=\sum_{n=1}^m\alpha_n\frac{r^{n\pi/\gamma}}{\rho^{n\pi/\gamma}} \sin\frac{n\pi\theta}{\gamma}\nonumber\]
satisface la Ecuación\ ref {eq:12.4.10} con
\[f(\theta) =\sum_{n=1}^m\alpha_n\sin\frac{n\pi\theta}{\gamma}.\nonumber\]
Esto nos motiva a definir la solución formal acotada de la Ecuación\ ref {eq:12.4.10} a ser
\[u_m(r,\theta)=\sum_{n=1}^\infty\alpha_n\frac{r^{n\pi/\gamma}}{\rho^{n\pi/\gamma}} \sin\frac{n\pi\theta}{\gamma},\nonumber\]
donde
\[S(\theta)=\sum_{n=1}^\infty\alpha_n \sin\frac{n\pi\theta}{\gamma}\nonumber\]
es la expansión sinusoidal de Fourier de\(f\) on\([0,\gamma]\); es decir,
\[\alpha_n=\frac{2}{\gamma}\int_0^\gamma f(\theta)\sin\frac{n\pi\theta}{\gamma}\,d\theta. \nonumber\]


