3.3.1: Ejemplos

Ejemplo 3.3.1.1: Ecuaciones de Beltrami

\ begin {eqnarray}
\ label {belt1}\ tag {3.3.1.1}
wu_x-bv_x-cv_y&=&0\
\ etiqueta {belt2}\ tag {3.3.1.2}
wu_y+av_x+bv_y&=&0,
\ end {eqnarray}

donde$W,\ a,\ b,\ c$ se dan funciones dependiendo de$(x,y)$,$W\not=0$ y la matriz

$$
\ left (\ begin {array} {cc}
a&b\\
b&c
\ end {array}\ derecha)
\]

es positivo definido.

El sistema Beltrami es una generalización de las ecuaciones de Cauchy-Riemann. La función$f(z)=u(x,y)+iv(x,y)$, donde$z=x+iy$, se denomina mapeo cuasiconforme, véase por ejemplo [9], Capítulo 12, para una aplicación a ecuaciones diferenciales parciales.

Set

$$
A^1=\ left (\ begin {array} {cc}
w&-b\\
0&a
\ end {array}\ right),\\
A^2=\ left (\ begin {array} {cc}
0&-c\\
w&b
\ end {array}\ right).
\]

Entonces el sistema (\ ref {belt1}), (\ ref {belt2}) puede escribirse como

$$
A^1\ left (\ begin {array} {c}
u_x\\ v_x
\ end {array}\ right) +
A^2\ left (\ begin {array} {c}
u_y\\ v_y
\ end {array}\ right) =\ left (\ begin {array} {c} 0\\ 0\ end {array}\ right).
\]

Por lo tanto,

\ begin {eqnarray*}
C (x, y,\ zeta) =\ izquierda|\ begin {array} {cc}
W\ zeta_1&-b\ zeta_1-c\ zeta_2\\
W\ zeta_2&a\ zeta_1+b\ zeta_2
\ end {array}\ derecha|
=W (a\ zeta_1^2+2b\ eta_1\ zeta_2+c\ zeta_2^2),
\ end {eqnarray*}

que es diferente de cero si de$\zeta\not=0$ acuerdo con los supuestos anteriores. Así el sistema Beltrami es elíptico.

Ejemplo 3.3.1.2: Ecuaciones Maxwell

Las ecuaciones de Maxwell en el caso isotrópico son

\ begin {eqnarray}
\ label {max1}\ tag {3.3.1.3}
c\\ texto {rot} _x\ H&=&\ lambda E+\ epsilon e_T\
\ etiqueta {max2}\ etiqueta {3.3.1.4}
c\\ texto {rot} _x\ E&=&-\ mu h_t,
\ end {eqnarray}

donde

• $E=(e_1,e_2,e_3)^T$intensidad de campo eléctrico,$e_i=e_i(x,t)$,$x=(x_1,x_2,x_3)$,
• $H=(h_1,h_2,h_3)^T$intensidad del campo magnético$h_i=h_i(x,t)$,
• $c$velocidad de la luz,
• $\lambda$conductividad específica,
• $\epsilon$constante de dielectricidad,
• $\mu$permeabilidad magnética.

Aquí$c,\ \lambda,\ \epsilon$ y$\mu$ son constantes positivas.

Establecer$p_0=\chi_t,\ p_i=\chi_{x_i}$,$i=1,\ldots 3$, entonces la ecuación diferencial característica es

$$
\ izquierda|\ begin {array} {cccccc}
\ epsilon p_0/c&0&0&0&p_3&-p_2\\
0&\ epsilon p_0/c&0&-p_3&0&p_1\\
0&0&\ epsilon p_0/c&p_2&-p_1&0\
0&-p_p_3&p_2&\ mu p_0/c&0&0\\
p_3&0&-p_1&0&\ mu p_0/c&0\\
-p_2&p_1&0&0&0&\ mu p_0/c
\ end {array}\ right|=0.
\]

Las siguientes manipulaciones simplifican esta ecuación:

1. multiplicar las tres primeras columnas con$\mu p_0/c$,
2. multiplicar la quinta columna con$-p_3$ y la sexta columna con$p_2$ y sumar la suma a la primera columna,
3. multiplicar la 4ta columna con$p_3$ y la sexta columna con$-p_1$ y sumar la suma a la 2ª columna,
4. multiplicar la 4ta columna con$-p_2$ y la quinta columna con$p_1$ y sumar la suma a la 3ª columna,
5. ampliar el determinante resultante con respecto a los elementos de la 6ª, 5ª y 4ª fila.

Obtenemos

$$
\ izquierda|\ begin {array} {ccc}
q+p_1^2&p_1p_2&p_1p_3\\
p_1p_2&q+p_2^2&p_2p_3\\
p_1p_3&p_2p_3&q+p_3^2
\ end {array}\ derecha|=0,
\]

donde

$$
q: =\ frac {\ épsilon\ mu} {c^2} p_0^2-g^2
\]

con$g^2:=p_1^2+p_2^2+p_3^2$. La evaluación de la ecuación anterior conduce a$q^2(q+g^2)=0$, es decir,

$$
\ chi_t^2\ left (\ frac {\ epsilon\ mu} {c^2}\ chi_t^2-|\ nabla_x\ chi|^2\ derecha) =0.
\]

De ello se deduce inmediatamente que las ecuaciones de Maxwell son un sistema hiperbólico, ver un ejercicio.
Hay dos soluciones de esta ecuación característica. El primero son superficies características$\mathcal{S}(t)$, definidas por$\chi(x,t)=0$, que satisfacen$\chi_t=0$. Estas superficies se llaman ondas estacionarias El segundo tipo de superficies características se definen por soluciones de

$$
\ frac {\ épsilon\ mu} {c^2}\ chi_t^2=|\ nabla_x\ chi|^2.
\]

Las funciones definidas por$\chi=f(n\cdot x-Vt)$ son soluciones de esta ecuación.
Aquí hay$f(s)$ una función arbitraria con$f'(s)\not=0$,$n$ es un vector unitario y$V=c/\sqrt{\epsilon\mu}$.
Las superficies características asociadas$\mathcal{S}(t)$ están definidas por

$$
\ chi (x, t)\ equiv f (n\ cdot x-VT) =0,
\]

aquí asumimos que$0$ está en el rango de$f:\ \mathbb{R}^1\mapsto\mathbb{R}^1$. Así,$\mathcal{S}(t)$ se define por$n\cdot x-Vt=c$, donde$c$ es una constante fija. De ello se deduce que los planos$\mathcal{S}(t)$ con normal$n$ se mueven con velocidad$V$ en dirección a$n$, ver Figura 3.3.1.1.

Figura 3.3.1.1:$d'(t)$ es la velocidad de las ondas planas

$V$se llama velocidad de la onda del avión$\mathcal{S}(t)$.

Obración. Según las discusiones anteriores, las singularidades de una solución de ecuaciones de Maxwell se ubican como máximo en superficies características.

Un caso especial de ecuaciones de Maxwell son las ecuaciones telegráficas, que se derivan de las ecuaciones de Maxwell if$\text{\div}\ E=0$ y$\text{div}\ H=0$$ i. e.,$E$ y$H$ son campos libres de fuentes. De hecho, es suficiente suponer que esta suposición se satisface en un tiempo fijo$t_0$ solamente, ver un ejercicio.

Desde

$$
\ text {rot} _x\\ texto {pudrición} _x\ A=\ mbox {grad} _x\\ texto {div} _x\ A-\ triangle_xA
\]

para cada campo$C^2$ -vector$A$, se deduce de las ecuaciones de Maxwell el sistema desacoplado

\ begin {eqnarray*}\ triangle_xe&=&\ frac {\ épsilon\ mu} {c^2} E_ {tt} +\ frac {\ lambda\ mu} {c^2} e_T\\
\ triangle_xh&=&\ frac {\ épsilon\ mu} {c^2} H_ {tt} +\ frac {\ lambda\ mu} {c^2} H_t.
\ end {eqnarray*}

Ejemplo 3.3.1.3: Ecuaciones de la Dinámica de Gases

Considera las siguientes ecuaciones cuasilineales de primer orden.

$$
v_t+ (v\ cdot\ nabla_x)\ v+\ frac {1} {\ rho}\ nabla_x p =f\\\\ mbox {(ecuaciones de Euler)}.
\]

Aquí está

• $v=(v_1,v_2,v_3)$el vector de velocidad,$v_i=v_i(x,t)$,$x=(x_1,x_2,x_3)$,
• $p$presión,$p=(x,t)$,
• $\rho$densidad,$\rho=\rho(x,t)$,
• $f=(f_1,f_2,f_3)$densidad de la fuerza externa$f_i=f_i(x,t)$,

$(v\cdot\nabla_x)v\equiv (v\cdot\nabla_x v_1,v\cdot\nabla_x v_2,v\cdot\nabla_x v_3))^T$.

La segunda ecuación es

$$
\ rho_t+v\ cdot\ nabla_x\ rho+\ rho\\ text {div} _x\ v=0\\\\ mbox {(conservación de la masa)}.
\]

Supongamos que el gas es compresible y que hay una función (ecuación de estado)

$$
p=p (\ rho),
\]

donde$p'(\rho)>0$ si$\rho>0$. Entonces el sistema anterior de cuatro ecuaciones es

\ begin {eqnarray}
\ label {euler}\ tag {3.3.1.5}
v_t+ (v\ cdot\ nabla) v+\ frac {1} {\ rho} p' (\ rho)\ nabla\ rho&=&f\
\ label {cont}\ tag {3.3.1.6}
\ rho_t+\ rho\ text {div}\ v+v\ cdot\ nabla\ rho&=&0,
\ end {eqnarray}

donde$\nabla\equiv\nabla_x$ y$\text{div}\equiv\text{div}_x$, i. e., estos operadores se aplican únicamente a las variables espaciales.

La ecuación diferencial característica está aquí
$$
\ izquierda|\ begin {array} {cccc}
\ frac {d\ chi} {dt} &0&0&\ frac {1} {\ rho} p'\ chi_ {x_1}\\
0&\ frac {d\ chi} {dt} &0&\ frac {1} {\ rho} p'\ chi_ {x_2}\\
0&0&\ frac {d\ chi} {dt} &\ frac {1} {\ rho} p'\ chi_ {x_3}\\
\ rho\ chi_ {x_1} &\ rho\ chi_ {x_2} &\ rho\ chi_ {x_3} &\ frac {d\ chi} {dt}
\ end {array}\ derecha|=0,
\]

donde

$$\ dfrac {d\ chi} {dt} :=\ chi_t+ (\ nabla_x\ chi)\ cdot v.\]

Evaluando el determinante, obtenemos la ecuación diferencial característica

\ begin {ecuación}
\ label {chargas}\ tag {3.3.1.7}
\ left (\ frac {d\ chi} {dt}\ right) ^2\ left (\ left (\ frac {d\ chi} {dt}\ right) ^2-p' (\ rho) |\ nabla_x\ chi|^2\ right) =0.
\ end {ecuación}

Esta ecuación implica consecuencias para la velocidad de las superficies características como lo demuestra la siguiente consideración.

Considere una familia$\mathcal{S}(t)$ de superficies$\mathbb{R}^3$ definidas por$\chi(x,t)=c$, donde
$x\in\mathbb{R}^3$ y$c$ es una constante fija. Como es habitual, suponemos que$\nabla_x\chi\not=0$.
Una de las dos normales$\mathcal{S}(t)$ en un punto de la superficie$\mathcal{S}(t)$ viene dada por, ver un ejercicio,
\ begin {ecuación}
\ label {surfnormal}\ tag {3.3.1.8}
{\ bf n} =\ frac {\ nabla_x\ chi} {|\ nabla_x\ chi|}.
\ end {ecuación}
Dejar$Q_0\in\mathcal{S}(t_0)$ y dejar$Q_1\in\mathcal{S}(t_1)$ ser un punto en la línea definida por$Q_0+s{\bf n}$, donde${\bf n}$ está la normal (\ ref {surfnormal}) on$\mathcal{S}(t_0)$ at$Q_0$ y$t_0<t_1$,$t_1-t_0$ pequeño, ver Figura 3.3.1.2.

3.3.1.2: Definición de la velocidad de una superficie

Definición. El límite
$$P=\ lim_ {t_1\ to t_0}\ frac {|Q_1-Q_0|} {t_1-t_0}$$
se llama velocidad de la superficie$\mathcal{S}(t)$.

Proposición 3.2. La velocidad de la superficie$\mathcal{S}(t)$ es
\ begin {ecuación}
\ label {speedsurf}
P=-\ frac {\ chi_t} {|\ nabla_x\ chi|}.
\ end {ecuación}

Comprobante. La prueba se desprende de$\chi(Q_0,t_0)=0$ y$\chi(Q_0+d{\bf n},t_0+\triangle t)=0$, dónde$d=|Q_1-Q_0|$ y$\triangle t=t_1-t_0$.

$\Box$

Establezca$v_n:=v\cdot{\bf n}$ cuál es el componente del vector de velocidad en dirección${\bf n}$.
De ({\ ref {surfnormal}) obtenemos
$$
v_n=\ frac {1} {|\ nabla_x\ chi|} v\ cdot\ nabla_x\ chi.
\]

Definición. $V:=P-v_n$, la diferencia de la velocidad de la superficie y la velocidad de las partículas líquidas, se denomina velocidad relativa.

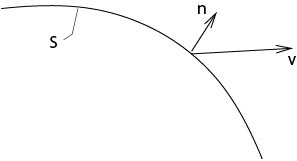
Figura 3.3.1.3: Definición de velocidad relativa

Usando las fórmulas anteriores para$P$ y$v_n$ sigue
$$v=p-v_n=-\ frac {\ chi_t} {|\ nabla_x\ chi|} -\ frac {v\ cdot\ nabla_x\ chi} {|\ nabla_x\ chi|} =-\ frac {1} {|\ nabla_x\ chi|}\ frac {d\ chi} dt}.$$
Entonces, obtenemos de la ecuación característica (\ ref {chargas}) que
$$V^2|\ nabla_x\ chi|^2\ left (V^2|\ nabla_x\ chi|^2-p' (\ rho) |\ nabla_x\ chi|^2\ right) =0.$$
Una conclusión interesante es que hay dos velocidades relativas:$V=0$ o$V^2=p'(\rho)$.

Definición. $\sqrt{p'(\rho)}$se llama velocidad del sonido.

Colaboradores y Atribuciones

• Template:ContribMiersemann
• Template:ContribMarshall