6.1: Fórmula de Poisson

Última actualización
Guardar como PDF

Page ID: 118023

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Supongamos que$u$ es una solución de (6.2), entonces, dado que la transformada de Fourier es un mapeo lineal,

\[\widehat{u_t-\triangle u}=\hat{0}.\]

De las propiedades de la transformada de Fourier, ver Proposición 5.1, tenemos

\[\widehat{\triangle u}=\sum_{k=1}^n\widehat{\frac{\partial^2 u}{\partial x_k^2}}=\sum_{k=1}^n i^2\xi^2_k\widehat{u}(\xi),\]

siempre que existan las transformaciones. Así llegamos a la ecuación diferencial ordinaria para la transformada de Fourier de$u$

\[\frac{d\widehat{u}}{dt}+|\xi|^2\widehat{u}=0,\]

donde$\xi$ se considera como un parámetro. La solución es

\[\widehat{u}(\xi,t)=\widehat{\phi}(\xi)e^{-|\xi|^2 t}\]

ya que$\widehat{u}(\xi,0)=\widehat{\phi}(\xi)$. Del Teorema 5.1 se sigue

\ begin {eqnarray*}
u (x, t) &=& (2\ pi) ^ {-n/2}\ int_ {\ mathbb {R} ^n}\\ sombrero ancho {\ phi} (\ xi) e^ {-|\ xi|^2t} e^ {i\ xi\ cdot x}\ d\ xi\
&=& (2\ pi) ^ {-^ -n}\ int_ {\ mathbb {R} ^n}\\ phi (y)\ izquierda (\ int_ {\ mathbb {R} ^n} e^ {i\ xi\ cdot (x-y) -|\ xi|^2t}\ d\ xi\ derecha)\ dy.
\ end {eqnarray*}

Set

$$K (x, y, t) = (2\ pi) ^ {-n}\ int_ {\ mathbb {R} ^n} e^ {i\ xi\ cdot (x-y) -|\ xi|^2t}\ d\ xi.\]

Por los mismos cálculos que en la prueba del Teorema 5.1, paso (vi), encontramos

\ begin {ecuación}
\ label {kernel1}
K (x, y, t) =( 4\ pi t) ^ {-n/2} e^ {-|x-y|^2/4t}.
\ end {ecuación}

Núcleo <span translate= \ (K (x, y, t)\),$\rho=|x-y|$,$t_1<t_2$ "height="213" width="403" src=” https://math.libretexts.org/@api/dek.../parabfig2.jpg "/>

Figura 6.1.1: Núcleo$K(x,y,t)$,$\rho=|x-y|$,$t_1<t_2$

Así tenemos

\ begin {ecuación}
\ label {poisson1}
u (x, t) =\ frac {1} {\ izquierda (2\ sqrt {\ pi t}\ derecha) ^n}\ int_ {\ mathbb {R} ^n}\ phi (z) e^ {-|x-z|^2/4t}\ dz.
\ end {ecuación}

Definición. La fórmula (\ ref {poisson1}) se llama fórmula de Poisson} y la función$K$ definida por (\ ref {kernel1}) se llama núcleo de calor o solución fundamental de la ecuación de calor.

Proposición 6.1 El kernel$K$ tiene las siguientes propiedades:

i)$K(x,y,t)\in C^\infty(\mathbb{R}^n\times\mathbb{R}^n\times\mathbb{R}^1_+)$,
ii)$(\partial/\partial t\ -\triangle)K(x,y,t)=0,\ t>0$,
iii)$K(x,y,t)>0,\ t>0$,
iv)$\int_{\mathbb{R}^n}\ K(x,y,t)\ dy=1$ $x\in\mathbb{R}^n$,$t>0$
$\delta>0$:( v) Por cada fijo

$$\ lim_ {\ begin {array} {l} t\ to0\ t>0\ end {array}}\ int_ {\ mathbb {R} ^n\ setmenos B_\ delta (x)}\ K (x, y, t)\ dy=0$$

uniformemente para$x\in\mathbb{R}$.

Comprobante. (i) y (iii) son obviamente, y (ii) se desprende de la definición de$K$. Las ecuaciones (iv) y (v) se mantienen desde

\ begin {eqnarray*}
\ int_ {\ mathbb {R} ^n\ setmenos B_\ delta (x)}\ K (x, y, t)\ dy&=&\ int_ {\ mathbb {R} ^n\ setmenos B_\ delta (x)}\ (4\ pi t) ^ {-n/2} e^ {-|x-y|2/4t}\ dy\\
&=&\ pi^ {-n/2}\ int_ {\ mathbb {R} ^n\ setmenos B_ {\ delta/\ sqrt {4t}} (0)} e^ {-|\ eta|^2}\ d\ eta
\ end { eqnarray*}
mediante el uso de la sustitución$y=x+(4t)^{1/2}\eta$. Para fijo$\delta>0$ sigue (v) y para$\delta:=0$ obtenemos (iv).

$\Box$

Teorema 6.1. Asumir$\phi\in C(\mathbb{R}^n)$ y$\sup_{\mathbb{R}^n}|\phi(x)|<\infty$. Entonces$u(x,t)$ dada por la fórmula de Poisson (\ ref {poisson1}) está en$C^{\infty}(\mathbb{R}^n\times\mathbb{R}^1_+)$, continua$\mathbb{R}^n\times[0,\infty)$ y una solución del problema de valor inicial (6.2), (6.3).

Comprobante. Queda por mostrar

$$
\ lim_ {\ begin {array} {l} x\ to\ xi\
t\ to0\ end {array}} u (x, t) =\ phi (\ xi).
\]

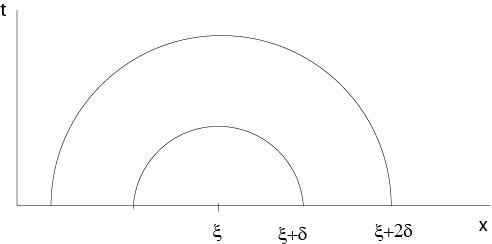
$Figura a la prueba del Teorema 6.1$

Figura 6.1.2: Figura a la prueba del Teorema 6.1

Ya que$\phi$ es continuo existe para dado$\varepsilon>0$ un$\delta=\delta(\varepsilon)$ tal que$|\phi(y)-\phi(\xi)|<\varepsilon$ si$|y-\xi|<2\delta$.
Set$M:=\sup_{\mathbb{R}^n}|\phi(y)|$. Entonces, ver Proposición 6.1,
$$
u (x, t) -\ phi (\ xi) =\ int_ {\ mathbb {R} ^n}\ K (x, y, t)\ izquierda (\ phi (y) -\ phi (\ xi)\ derecha)\ dy.
$$
Se deduce, si$|x-\xi|<\delta$ y$t>0$, que
\ begin {eqnarray*}
|u (x, t) -\ phi (\ xi) |&\ le&\ int_ {B_ {\ delta} (x)}\ K (x, y, t)\ izquierda|\ phi (y) -\ phi (\ xi)\ derecha|\ dy\
&&+\ int_ {\ mathbb {} ^n\ setmenos B_ {\ delta} (x)}\ K (x, y, t) \ izquierda|\ phi (y) -\ phi (\ xi)\ derecha|\ dy\
&\ le&\ int_ {B_ {2\ delta} (x)}\ K (x, y, t)\ izquierda|\ phi (y) -\ phi (\ xi)\ derecha|\ dy\
&&&+2M\ int_ {\ mathbb {R} ^n\ setmenos _ {\ delta} (x)}\ K (x, y, t)\ dy\\
&\ le&\ varepsilon\ int_ {\ mathbb {R} ^n}\ K (x, y, t)\ dy+2m\ int_ {\ mathbb {R} ^n\ setmenos B_ {\ delta} (x)}\ K (x, y, t)\ dy\\
&<&2\ varepsilon
\ end {eqnarray*}
si$0<t\le t_0$,$t_0$ suficientemente pequeño.

$\Box$

Observaciones. 1. La singularidad sigue bajo el supuesto de crecimiento adicional
$$
|u (x, t) |\ le Me^ {a|x|^2}\\\ mbox {in}\ D_T,
$$
donde$M$ y$a$ son constantes positivas,
vea la Proposición 6.2 a continuación.
En el caso unidimensional, uno tiene singularidad en la clase$u(x,t)\ge 0$ en$D_T$, ver [10], pp. 222.

2. $u(x,t)$definido por la fórmula de Poisson depende de todos los valores$\phi(y)$,$y\in\mathbb{R}^n$. Eso quiere decir, una perturbación de$\phi$, incluso lejos de una fija$x$, influye en el valor$u(x,t)$. Esto significa que el calor viaja con una velocidad infinita, en contraste con la experiencia.