7.1: Coordenadas polares

Última actualización
Guardar como PDF

Page ID: 113827

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Las coordenadas polares en dos dimensiones se definen\[\begin{aligned} x = \rho\cos\phi, y= \rho\sin\phi,\\ \rho = \sqrt{x^2+y^2}, \phi = \arctan(y/x),\end{aligned} \nonumber \] como se indica esquemáticamente en la Fig. \(\PageIndex{1}\).

Figura\(\PageIndex{1}\): Coordenadas polares

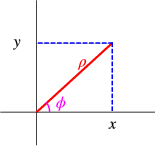
Usando la regla de la cadena encontramos

\[\begin{aligned} \frac{\partial}{\partial x}{~} &= \frac{\partial \rho}{\partial x}\frac{\partial}{\partial \rho}{~}+\frac{\partial \phi}{\partial x}\frac{\partial}{\partial \phi}{~}\nonumber\\ &= \frac{x}{\rho}\frac{\partial}{\partial \rho}{~}-\frac{y}{\rho^2}\frac{\partial}{\partial \phi}{~}\nonumber\\ &= \cos\phi\frac{\partial}{\partial \rho}{~}-\frac{\sin\phi}{\rho}\frac{\partial}{\partial \phi}{~},\\ \frac{\partial}{\partial y}{~} &= \frac{\partial \rho}{\partial y}\frac{\partial}{\partial \rho}{~}+\frac{\partial \phi}{\partial y}\frac{\partial}{\partial \phi}{~}\nonumber\\ &= \frac{y}{\rho}\frac{\partial}{\partial \rho} {~}+\frac{x}{\rho^2}\frac{\partial}{\partial \phi}{~}\nonumber\\ &= \sin\phi\frac{\partial}{\partial \rho}{~}+\frac{\cos\phi}{\rho}\frac{\partial}{\partial \phi}{~},\end{aligned} \nonumber \]Podemos escribir\[\begin{aligned} {\nabla} &= {\hat{e}}_\rho \frac{\partial}{\partial \rho}{~}+\hat{e}_\phi \frac{1}{\rho} \frac{\partial}{\partial \phi}{~}\end{aligned} \nonumber \]

donde los vectores unitarios

\[\begin{aligned} \hat{e}_\rho &= (\cos\phi,\sin\phi), \nonumber\\ \hat{e}_\phi &= (-\sin\phi,\cos\phi), \end{aligned} \nonumber \]son un conjunto ortonormal. Decimos que las coordenadas circulares son ortogonales.

Ahora podemos usar esto para evaluar\(\nabla^2\),

\[\begin{aligned} \nabla^2 &= \cos^2\phi\frac{\partial^2}{\partial \rho^2}{~} + \frac{\sin\phi\cos\phi}{\rho^2}\frac{\partial}{\partial \phi} {~} +\frac{\sin^2\phi}{\rho}\frac{\partial}{\partial \rho} {~} + \frac{\sin^2\phi}{\rho^2}\frac{\partial^2}{\partial \phi^2} {~} + \frac{\sin\phi\cos\phi}{\rho^2} \frac{\partial}{\partial \phi} {~}\nonumber\\ &\space\space\space+\sin^2\phi\frac{\partial^2}{\partial \rho^2} {~}-\frac{\sin\phi\cos\phi}{\rho^2}\frac{\partial}{\partial \phi} {~} +\frac{\cos^2\phi}{\rho}\frac{\partial}{\partial \rho} {~} + \frac{\cos^2\phi}{\rho^2}\frac{\partial^2}{\partial \phi^2} {~} - \frac{\sin\phi\cos\phi}{\rho^2} \frac{\partial}{\partial \phi}{~}\\ &=\frac{\partial^2}{\partial \rho^2} {~} +\frac{1}{\rho}\frac{\partial}{\partial \rho}{~} + \frac{1}{\rho^2}\frac{\partial^2}{\partial \phi^2} {~}\nonumber\\ &=\frac{1}{\rho}\frac{\partial}{\partial \rho} {~} \left(\rho\frac{\partial}{\partial \rho} {~}\right) +\frac{1}{\rho^2}\frac{\partial^2}{\partial \phi^2} {~}.\nonumber\\\end{aligned} \nonumber \]

Una relación útil final es la integración sobre estas coordenadas.

Figura\(\PageIndex{2}\): Integración en coordenadas polares

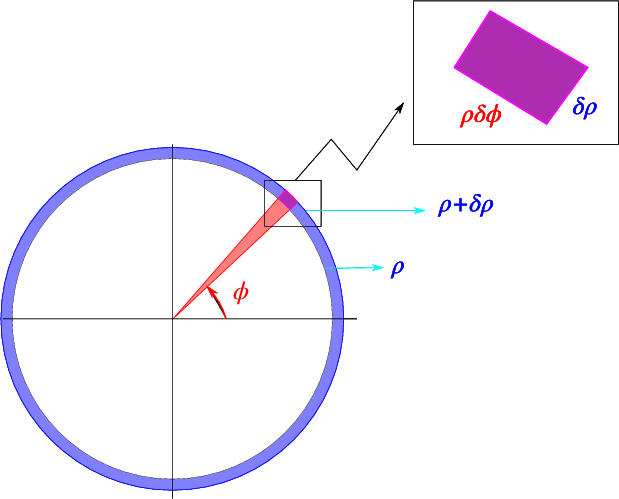
Como se indica esquemáticamente en la Fig. \(\PageIndex{2}\), la superficie relacionada con un cambio\(\rho \rightarrow \rho + \delta \rho\),\(\phi \rightarrow \phi+\delta\phi\) es\(\rho \delta \rho \delta\phi\). Esto nos lleva a la conclusión de que una integral sobre\(x,y\) puede reescribirse como\[\int_V f(x,y) dx dy = \int_V f(\rho\cos\phi,\rho\sin\phi) \rho \,d\rho\, d\phi \nonumber \]