1.1: Caída Libre

En este capítulo estudiaremos algunas ecuaciones diferenciales comunes que aparecen en la física. Comenzaremos con los tipos más simples de ecuaciones y técnicas estándar para resolverlas Terminaremos esta parte de la discusión volviendo al problema de la caída libre con resistencia al aire. Pasaremos entonces al estudio de las oscilaciones, las cuales son modeladas por ecuaciones diferenciales de segundo orden.

Ejemplo de caída libre.

Comencemos con un ejemplo sencillo de la física introductoria. Recordemos que la caída libre es el movimiento vertical de un objeto únicamente bajo la fuerza de la gravedad. Se ha determinado experimentalmente que un objeto cercano a la superficie de la Tierra cae a una aceleración constante en ausencia de otras fuerzas, como la resistencia al aire. Esta aceleración constante se denota por\(-g\), donde\(g\) se llama la aceleración debido a la gravedad. El signo negativo es una indicación de que hemos elegido un sistema de coordenadas en el que arriba es positivo.

Nos interesa determinar la posición,\(y(t)\), del cuerpo que cae en función del tiempo. A partir de la definición de caída libre, tenemos

\[\ddot{y}(t)=-g \label{1.1}. \]

Tenga en cuenta que ocasionalmente usaremos un punto para indicar la diferenciación de tiempo.

La diferenciación con respecto al tiempo a menudo se denota por puntos en lugar de primos.

Esta notación es estándar en física y comenzaremos a presentarle esta notación, aunque a veces podríamos usar la notación prima más familiar para indicar diferenciación espacial, o diferenciación general.

En Ecuación\(\PageIndex{1}\) sabemos\(g\). Es una constante. Cerca de la superficie de la Tierra se trata de\(9.81 \mathrm{~m} / \mathrm{s}^{2}\) o\(32.2 \mathrm{ft} / \mathrm{s}^{2}\). Lo que no sabemos es\(y(t)\). Esta es nuestra primera ecuación diferencial. De hecho, es natural ver las ecuaciones diferenciales aparecer en la física a menudo a través de la Segunda Ley de Newton\(F=m a\), ya que juega un papel importante en la física clásica. Volveremos a este punto más adelante.

Entonces, ¿cómo se resuelve la ecuación diferencial en\(\PageIndex{1}\)? Lo hacemos usando lo que sabemos sobre el cálculo. Podría ser más fácil de ver cuando ponemos en un número determinado en lugar de\(g\). Es posible que aún se esté acostumbrando al hecho de que algunas letras se utilizan para representar constantes. Volveremos a la forma más general después de ver cómo resolver la ecuación diferencial.

Considerar

\[\ddot{y}(t)=5. \nonumber \]

Recordando que la segunda derivada es solo la derivada de una derivada, podemos reescribir esta ecuación como

\[\dfrac{d}{d t}\left(\dfrac{d y}{d t}\right)=5 \nonumber \]

Esto nos dice que la derivada de\(d y / d t\) es 5. ¿Se te ocurre una función cuya derivada es 5? (No hay que olvidar que la variable independiente es\(t\).) Sí, el derivado de\(5 t\) con respecto a\(t\) es 5. ¿Es esta la única función cuya derivada es 5? ¡No! También se puede diferenciar\(5 t+1,5 t+\pi, 5 t-6\), etc. en general, la derivada de\(5 t+C\) es 5, donde\(C\) es una constante de integración arbitraria.

Por lo tanto, la ecuación se\(\PageIndex{2}\) puede reducir a

\[\dfrac{d y}{d t}=5 t+C \nonumber \]

Ahora te preguntamos si conoces una función cuya derivada es\(5 t+C\). Bueno, tal vez puedas hacer esto en tu cabeza, pero solo necesitamos recordar el Teorema Fundamental del Cálculo, que relaciona integrales y derivadas. Por lo tanto, tenemos

\[y(t)=\dfrac{5}{2} t^{2}+C t+D \nonumber \]

donde\(D\) es una segunda constante de integración.

La ecuación\(\PageIndex{5}\) da la solución a la ecuación diferencial original. Eso significa que cuando la solución se coloca en la ecuación diferencial, ambos lados de la ecuación diferencial dan la misma expresión. Siempre puedes verificar tu respuesta a una ecuación diferencial mostrando que tu solución satisface la ecuación. En este caso tenemos

\(\ddot{y}(t)=\dfrac{d^{2}}{d t^{2}}\left(\dfrac{5}{2} t^{2}+C t+D\right)=\dfrac{d}{d t}(5 t+C)=5\)

Por lo tanto, Ecuación\(\PageIndex{5}\) da la solución general de la ecuación diferencial.

También vemos que hay dos constantes arbitrarias,\(C\) y\(D .\) Escogiendo cualquier valor para estas da toda una familia de soluciones. Como veremos, la ecuación\(\ddot{y}(t)=5\) es una ecuación diferencial ordinaria lineal de segundo orden. La solución general de tal ecuación siempre tiene dos constantes arbitrarias.

Volvamos al problema de la caída libre. Lo resolvemos de la misma manera. La única diferencia es que podemos sustituir la constante 5 por la constante\(-g .\) Entonces, encontramos que

\[\dfrac{d y}{d t}=-g t+C \nonumber \]

y

\[y(t)=-\dfrac{1}{2} g t^{2}+C t+D \nonumber \]

Una vez que bajas el proceso, solo se necesita una o dos líneas para resolverlo.

Parece que hay un problema. Imagínese dejar caer una pelota que luego sufre caída libre. ¡Acabamos de determinar que hay un número infinito de soluciones para la posición de la pelota en cualquier momento! Bueno, eso no es posible. La experiencia nos dice que si sueltas una pelota esperas que se comporte de la misma manera cada vez. ¿O lo hace? En realidad, podrías dejar caer la pelota desde cualquier lugar. También podrías tirarlo hacia arriba o tirarlo hacia abajo. Entonces, hay muchas maneras de soltar la pelota antes de que esté en caída libre produciendo muchos caminos diferentes,\(y(t)\). Ahí es donde entran las constantes. Tienen significados físicos.

Si pones\(t=0\) en la ecuación, entonces tienes eso\(y(0)=D .\) Así,\(D\) da la posición inicial de la pelota. Típicamente, denotamos valores iniciales con un subíndice. Entonces, vamos a escribir\(y(0)=y_{0}\). Por lo tanto,\(D=y_{0}\).

Eso nos deja determinar\(C\). Aparece al principio en Ecuación\(\PageIndex{6}\). Recordemos que\(\dfrac{d y}{d t}\), la derivada de la posición, es la velocidad vertical,\(v(t)\). Es positivo cuando la pelota se mueve hacia arriba. Denotaremos la velocidad inicial\(v(0)=v_{0} .\) Insertando\(t=0\) en Ecuación\(\PageIndex{6}\), nos encontramos con eso\(\dot{y}(0)=C\). Esto implica que\(C=v(0)=v_{0}\).

Armando todo esto, tenemos la forma física de la solución para la caída libre como

\[y(t)=-\dfrac{1}{2} g t^{2}+v_{0} t+y_{0} \nonumber \]

¿No le resulta familiar esta ecuación? Ahora vemos que la familia infinita de soluciones consiste en caída libre resultante de dejar caer inicialmente una bola en posición\(y_{0}\) con velocidad inicial\(v_{0}\). Las condiciones\(y(0)=y_{0}\) y\(\dot{y}(0)=v_{0}\) se llaman las condiciones iniciales. Una solución de una ecuación diferencial que satisface un conjunto de condiciones iniciales se denomina a menudo una solución particular. Especificar las condiciones iniciales da como resultado una solución única.

Entonces, hemos resuelto la ecuación de caída libre. En el camino hemos comenzado a ver algunas de las características que aparecerán en las soluciones de otros problemas que se modelan con ecuación diferencial. A lo largo del libro veremos varias aplicaciones de ecuaciones diferenciales. Extenderemos nuestro análisis a dimensiones superiores, en las que en este caso nos enfrentaremos a las denominadas ecuaciones diferenciales parciales, que involucran las derivadas parciales de funciones de más de una variable.

Pero ¿terminamos con la caída libre? ¡En absoluto! Podemos relajar algunas de las condiciones que hemos impuesto. Podemos agregar resistencia al aire. Visitaremos este problema más adelante en este capítulo después de introducir algunas técnicas más. También podemos proporcionar un componente horizontal de movimiento, lo que lleva al movimiento del proyectil.

Figura\(\PageIndex{1}\): Caída libre lejos de la Tierra desde una altura\(h(t)\) de la superficie.

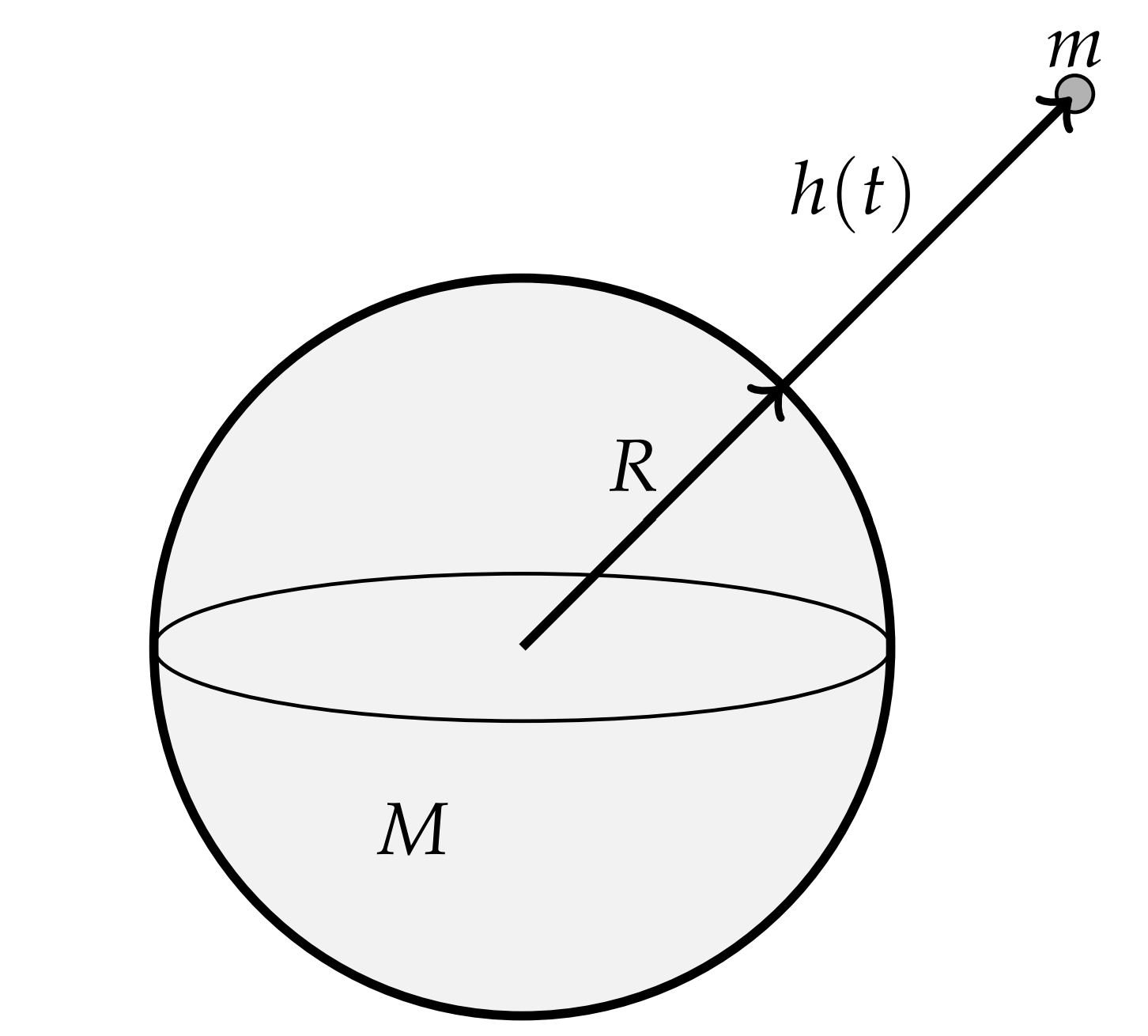
Por último, también hay que señalar que la caída libre a constante\(g\) sólo tiene lugar cerca de la superficie de la Tierra. ¿Y si un azulejo se cae del transbordador lejos de la superficie de la Tierra? También caerá hacia la Tierra. En realidad, la baldosa también tiene un componente de velocidad en la dirección del movimiento de la lanzadera. Entonces, no necesariamente tomaría trayectoria radial hacia abajo. Por ahora, ignoremos ese componente. Para ver este problema con más detalle, necesitamos ir a los orígenes de la aceleración por gravedad. Esto sale de la Ley de Gravitación de Newton. Considera una masa\(m\) a cierta\(h(t)\) distancia de la superficie de la Tierra (esférica). Dejando\(M\) y\(R\) siendo la masa y el radio de la Tierra, respectivamente, la Ley de Gravitación de Newton establece que

\[ \begin{aligned} m a &=F \\ m \dfrac{d^{2} h(t)}{d t^{2}} &=-G \dfrac{m M}{(R+h(t))^{2}} \end{aligned} \nonumber \]

Aquí\(G=6.6730 \times 10^{-11} \mathrm{~m}^{3} \mathrm{~kg}^{-1} \mathrm{~s}^{-2}\) está la Constante Gravitacional Universal,\(M=5.9736 \times 10^{24} \mathrm{~kg}\) y\(R=6371 \mathrm{~km}\) están la masa y el radio medio de la Tierra, respectivamente. Para\(h<<R, G M / R^{2} \approx g\).

Así, llegamos a una ecuación diferencial

\[\dfrac{d^{2} h(t)}{d t^{2}}=-\dfrac{G M}{(R+h(t))^{2}} . \nonumber \]

Esta ecuación no es tan fácil de resolver. Lo dejaremos como un ejercicio de tarea para el lector.