1.2: Ecuaciones diferenciales de primer orden
- Page ID
- 119649
\(n\)Ecuación diferencial ordinaria de orden -ésimo.
ANTES DE PASAR, DEFINIMOS PRIMERO una ecuación ordinaria de orden\(n\) -ésimo. Es una ecuación para una función desconocida\(y(x)\) una relación entre la función desconocida y sus primeras\(n\) derivadas. Uno podría escribir esto generalmente como
\[F\left(y^{(n)}(x), y^{(n-1)}(x), \ldots, y^{\prime}(x), y(x), x\right)=0 \nonumber \]
Aquí\(y^{(n)} (x)\) representa la derivada\(n\) th de y (x).
Problema de valor inicial.
Un problema de valor inicial consiste en la ecuación diferencial más los valores de las primeras\(n-1\) derivadas a un valor particular de la variable independiente, digamos\(x_{0}\):
\[y^{(n-1)}\left(x_{0}\right)=y_{n-1}, \quad y^{(n-2)}\left(x_{0}\right)=y_{n-2}, \quad \ldots, \quad y\left(x_{0}\right)=y_{0} \nonumber \]
Ecuación diferencial lineal de orden\(n\) th.
Una ecuación diferencial lineal de orden\(n\) th toma la forma
\[\left.a_{n}(x) y^{(n)}(x)+a_{n-1}(x) y^{(n-1)}(x)+\ldots+a_{1}(x) y^{\prime}(x)+a_{0}(x) y(x)\right)=f(x) \nonumber \]
Ecuaciones homogéneas y no homogéneas.
Si\(f(x) \equiv 0\), entonces se dice que la ecuación es homogénea, de lo contrario se llama no homogénea.
Ecuación diferencial de primer orden.
Por lo general, las primeras ecuaciones diferenciales encontradas son ecuaciones de primer orden. Una ecuación diferencial de primer orden toma la forma
\[F\left(y^{\prime}, y, x\right)=0 \nonumber \]
Existen dos ecuaciones diferenciales comunes de primer orden para las cuales se puede obtener formalmente una solución. El primero es el caso separable y el segundo es una ecuación de primer orden. Indicamos que podemos obtener soluciones formalmente, ya que se puede mostrar la integración necesaria que conduce a una solución. Sin embargo, las integrales resultantes no siempre son reducibles a funciones elementales ni se obtienen soluciones explícitas cuando las integrales son factibles.
Ecuaciones separables
UNA ECUACIÓN DE PRIMER ORDEN ES SEPARABLE si se puede escribir el formulario
\[\dfrac{d y}{d x}=f(x) g(y) \nonumber \]
Los casos especiales resultan cuando cualquiera\(f(x)=1\) o\(g(y)=1 .\) En el primer caso se dice que la ecuación es autónoma.
Ecuaciones separables. La solución general a la ecuación\(\PageIndex{5}\) se obtiene en términos de dos integrales:
\[\int \dfrac{d y}{g(y)}=\int f(x) d x+C, \nonumber \]
donde\(C\) es una constante de integración. Esto produce una familia de soluciones de 1 parámetro a la ecuación diferencial correspondiente a diferentes valores de C. Si uno puede resolver Ecuación\(\PageIndex{6}\) para\(y(x)\), entonces se obtiene una solución explícita. De lo contrario, se tiene una familia de soluciones implícitas. Si también se da una condición inicial, entonces uno podría ser capaz de encontrar un miembro de la familia que satisfaga esta condición, que a menudo se llama una solución particular.
\(y^{\prime}=2 x y, y(0)=2\).
Aplicando la ecuación\(\PageIndex{6}\), uno tiene
\(\int \dfrac{d y}{y}=\int 2 x d x+C\)
Rendimientos entrelazados
\(ln \lvert y \rvert = x^2 +C.\)
Exponenciando, se obtiene la solución general,
\(y(x)=\pm e^{x^{2}+C}=A e^{x^{2}}\)
Aquí hemos definido\(A=\pm e^{C}\). Dado que\(C\) es una constante arbitraria,\(A\) es una constante arbitraria. Varias soluciones en esta familia de 1 parámetros se muestran en la Figura\(\PageIndex{1}\).
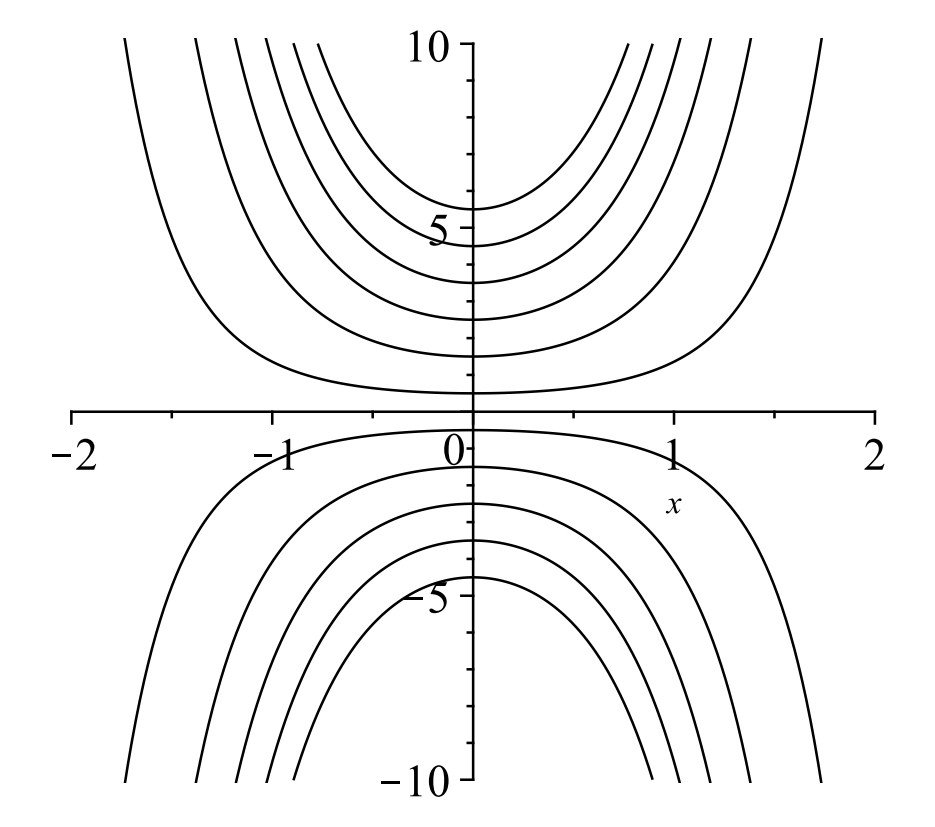
A continuación, se busca una solución particular que satisfaga la condición inicial. Porque\(y(0)=2\), uno encuentra\(A=2 .\) que So, la solución particular que satisface la condición inicial es\(y(x)=2 e^{x^{2}}\).
\(y y^{\prime}=-x .\)Siguiendo el mismo procedimiento que en el último ejemplo, se obtiene:
\(\int y d y=-\int x d x+C \Rightarrow y^{2}=-x^{2}+A, \quad \text { where } \quad A=2 C\)
Entonces obtenemos una solución implícita. Escribiendo la solución como\(x^{2}+y^{2}=\)
Así, obtenemos una solución implícita. Escribiendo la solución como\(x^{2}+y^{2}=\)\(A\), vemos que esta es una familia de círculos para\(A>0\) y el origen para\(A=0 .\) Parcelas de algunas soluciones en esta familia se muestran en la Figura\(\PageIndex{2}\).
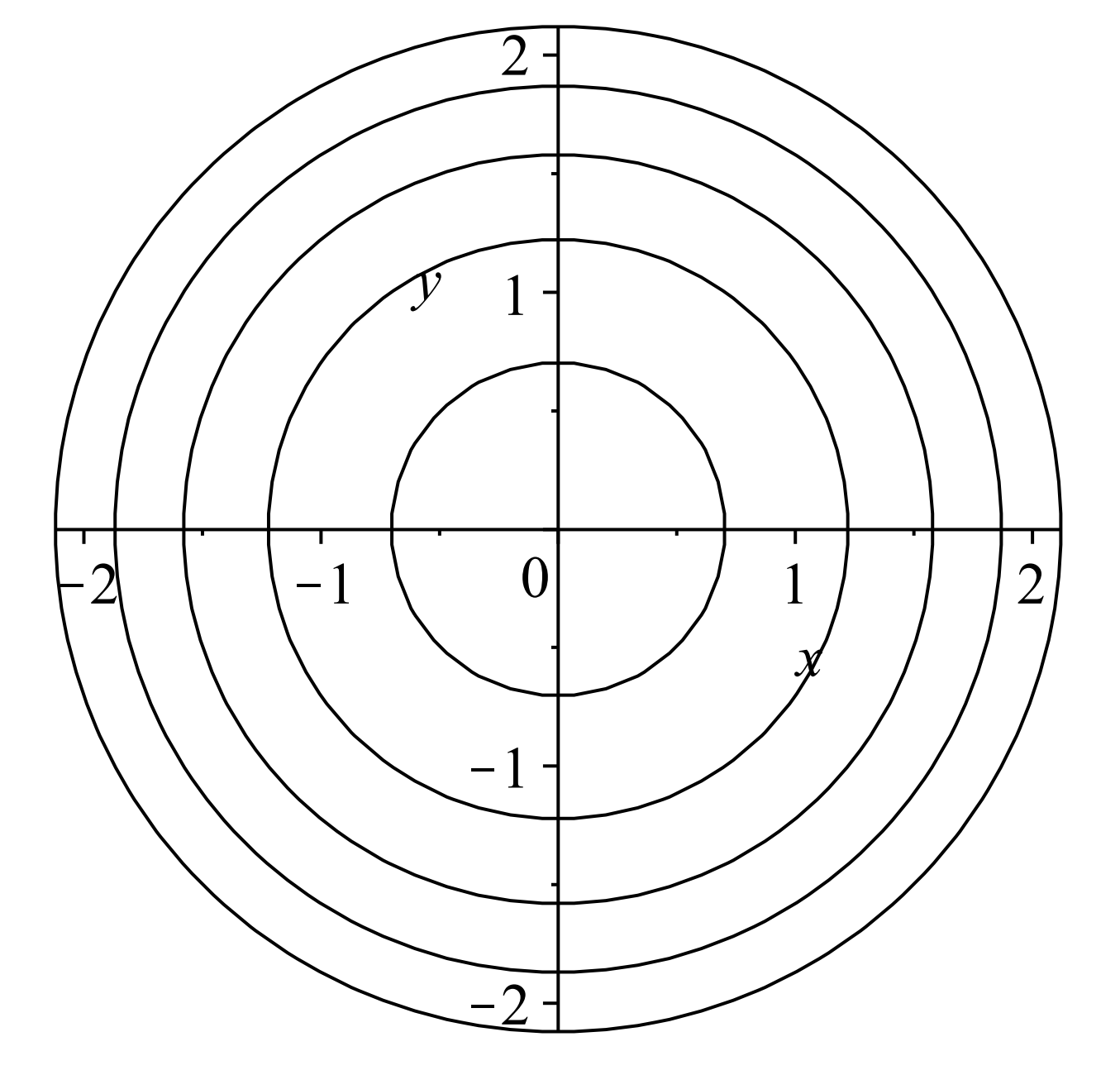
Ecuaciones Lineales de Primer Orden
EL SEGUNDO TIPO DE ECUACIÓN DE PRIMER ORDEN encontrada es la ecuación diferencial lineal de primer orden en la forma estándar
\[y^{\prime}(x)+p(x) y(x)=q(x) \nonumber \]
En este caso se busca un factor integrador\(\mu(x)\), que es una función que se puede multiplicar a través de la ecuación haciendo del lado izquierdo una derivada perfecta. De esta manera, obtener,
\[\dfrac{d}{d x}[\mu(x) y(x)]=\mu(x) q(x) \nonumber \]
El factor integrador que funciona es\(\mu(x)=\exp \left(\int^{x} p(\xi) d \xi\right) .\) Uno puede derivar\(\mu(x)\) expandiendo la derivada en Ecuación\(\PageIndex{8}\),
\[\mu(x) y^{\prime}(x)+\mu^{\prime}(x) y(x)=\mu(x) q(x) \nonumber \]
y comparando esta ecuación con la obtenida de multiplicar\(\PageIndex{7}\) por\(\mu(x):\)
\[\mu(x) y^{\prime}(x)+\mu(x) p(x) y(x)=\mu(x) q(x) \nonumber \]
Obsérvese que estas dos últimas ecuaciones serían las mismas si los segundos términos fueran los mismos. Por lo tanto, vamos a requerir que
\[\dfrac{d \mu(x)}{d x}=\mu(x) p(x) \nonumber \]
Factor integrador.
Esta es una ecuación separable de primer orden para\(\mu(x)\) cuya solución es el factor integrador:
\[\mu(x)=\exp \left(\int^{x} p(\xi) d \xi\right) \nonumber \]
\(\PageIndex{8}\)La ecuación ahora se integra fácilmente para obtener la solución general a la ecuación diferencial lineal de primer orden:
\[y(x)=\dfrac{1}{\mu(x)}\left[\int^{x} \mu(\xi) q(\xi) d \xi+C\right] \nonumber \]
\(x y^{\prime}+y=x, \quad x>0, y(1)=0\).
Uno primero señala que se trata de una ecuación diferencial lineal de primer orden. Resolviendo para\(y^{\prime}\), se puede ver que la ecuación no es separable. Además, no está en la forma estándar\(\PageIndex{7}\). Entonces, primero reescribimos la ecuación como
\[\dfrac{d y}{d x}+\dfrac{1}{x} y=1 \nonumber \]
Señalando que\(p(x)=\dfrac{1}{x}\), determinamos el factor integrador
\[\mu(x)=\exp \left[\int^{x} \dfrac{d \xi}{\xi}\right]=e^{\ln x}=x\nonumber \]
Multiplicando la ecuación\(\PageIndex{13}\) por\(\mu(x)=x\), ¡en realidad recuperamos la ecuación original! En este caso hemos encontrado que\(x y^{\prime}+y\) debió haber sido el derivado de algo para comenzar. De hecho,\((x y)^{\prime}=x y^{\prime}+x\). Por lo tanto, la ecuación diferencial se convierte en
\((x y)^{\prime}=x .\)
Integrando, se obtiene
\(x y=\dfrac{1}{2} x^{2}+C\)
O
\(y(x)=\dfrac{1}{2} x+\dfrac{C}{x}\)
Insertando la condición inicial en esta solución, tenemos\(0=\dfrac{1}{2}+C\). Por lo tanto,\(C=-\dfrac{1}{2}\). Así, la solución del problema del valor inicial es
\(y(x)=\dfrac{1}{2}\left(x-\dfrac{1}{x}\right)\)
Podemos verificar que esta es la solución. Desde entonces\(y^{\prime}=\dfrac{1}{2}+\dfrac{1}{2 x^{2}}\), tenemos
\(x y^{\prime}+y=\dfrac{1}{2} x+\dfrac{1}{2 x}+\dfrac{1}{2}\left(x-\dfrac{1}{x}\right)=x .\)
También,\(y(1)=\dfrac{1}{2}(1-1)=0\).
\((\sin x) y^{\prime}+(\cos x) y=x^{2}\).
En realidad, este problema es fácil si te das cuenta de que el lado izquierdo es un derivado perfecto. A saber,
\(\dfrac{d}{d x}((\sin x) y)=(\sin x) y^{\prime}+(\cos x) y\)
Pero, pasaremos por el proceso de encontrar el factor integrador para la práctica.
Primero, reescribimos la ecuación diferencial original en forma estándar. Dividimos la ecuación por\(\sin x\) para obtener
\(y^{\prime}+(\cot x) y=x^{2} \csc x\)
Luego, calculamos el factor integrador como
\ [\(\mu(x)=\exp \left(\int^{x} \cot \xi d \xi\right)=e^{\ln (\sin x)}=\sin x\)
Usando el factor de integración, la ecuación de forma estándar se convierte
\(\dfrac{d}{d x}((\sin x) y)=x^{2}\)
Integrando, tenemos
\(y \sin x=\dfrac{1}{3} x^{3}+C\)
Entonces, la solución es
\(y(x)=\left(\dfrac{1}{3} x^{3}+C\right) \csc x\)
Hay otras ecuaciones de primer orden que se pueden resolver para soluciones de forma cerrada. Sin embargo, muchas ecuaciones no son solucionables, o una simplemente está interesada en el comportamiento de las soluciones. En tales casos se gira a campos de dirección o métodos numéricos. Volveremos a una discusión sobre el comportamiento cualitativo de las ecuaciones diferenciales más adelante y las soluciones numéricas de las ecuaciones diferenciales ordinarias más adelante en el libro.
Ecuaciones diferenciales exactas
Algunas ecuaciones diferenciales de primer orden se pueden resolver fácilmente si son lo que se llama ecuaciones diferenciales exactas. Estas ecuaciones se escriben típicamente usando diferenciales. Por ejemplo, la ecuación diferencial
\[N(x, y) \dfrac{d y}{d x}+M(x, y)=0 \nonumber \]
se puede escribir en el formulario
\(M(x, y) d x+N(x, y) d y=0\)
Esto se ve multiplicando Ecuación\(\PageIndex{14}\) por\(d x\) y señalando a partir del cálculo que para una función\(y=y(x)\), la relación entre los diferenciales\(d x\) y\(d y\) es
\(d y=\dfrac{d y}{d x} d x\)
Diferencial de formas únicas. La expresión\(M(x, y) d x+N(x, y) d y\) se llama una única forma diferencial. Tal forma única se llama exacta si hay una función\(u(x, y)\) tal que
\(M(x, y) d x+N(x, y) d y=d u\)
Exacto de una forma. Sin embargo, a partir del cálculo sabemos que para cualquier función\(u(x, y)\),
\(d u=\dfrac{\partial u}{\partial x} d x+\dfrac{\partial u}{\partial y} d y\)
Si\(d u=M(x, y) d x+N(x, y) d y\), entonces tenemos
\[ \begin{aligned} &\dfrac{\partial u}{\partial x}=M(x, y) \\ &\dfrac{\partial u}{\partial y}=N(x, y) \end{aligned}\label{1.25} \]
Desde
\(\dfrac{\partial^{2} u}{\partial x \partial y}=\dfrac{\partial^{2} u}{\partial y \partial x}\)
cuando estas segundas derivadas son continuas, por el Teorema de Clairaut, entonces tenemos
\(\dfrac{\partial M}{\partial y}=\dfrac{\partial N}{\partial x}\)
debe sostenerse si\(M(x, y) d x+N(x, y) d y\) va a ser una forma exacta.
En resumen, hemos encontrado que
Condiciones para\(M(x, y) d x+N(x, y) d y=0\) to be exact
La ecuación diferencial\(M(x, y) d x+N(x, y) d y=0\) es exacta en el dominio\(D\) del\(x y\) -plano para\(M, N, M_{y}\), y las funciones\(N_{x}\) continuas en\(D\) if y only if
\(\dfrac{\partial M}{\partial y}=\dfrac{\partial N}{\partial x}\)
sostiene en el dominio.
Además, si\(d u=M(x, y) d x+N(x, y) d y=0\), entonces\(u(x, y)=C\), por\(C\) una constante arbitraria. Así, se puede encontrar una solución implícita como
\(\int_{x_{0}}^{x} M(x, y) d x+\int_{y_{0}}^{y} N(x, y) d y=C\)
Esto lo mostramos en el siguiente ejemplo.
Mostrar que\(\left(x^{3}+x y^{2}\right) d x+\left(x^{2} y+y^{3}\right) d y=0\) es una ecuación diferencial exacta y obtener la solución implícita correspondiente
Primero notamos que
\(\dfrac{\partial M}{\partial y}=2 x y, \quad \dfrac{\partial N}{\partial x}=2 x y\)
Dado que estas derivadas parciales son las mismas, la ecuación diferencial es exacta. Entonces, necesitamos encontrar la función de\(u(x, y)\) tal manera que\(d u=\left(x^{3}+\right.\)\(\left.x y^{2}\right) d x+\left(x^{2} y+y^{3}\right) d y .\)
En primer lugar, señalamos que\(x^{3}=d\left(\dfrac{x^{4}}{4}\right)\) y\(y^{3}=d\left(\dfrac{y^{4}}{4}\right)\). Los términos restantes se pueden combinar para encontrar que
\[ \begin{aligned} x y^{2} d x+x^{2} y d y &=x y(y d x+x d y) \\ &=x y d(x y) \\ &=d\left(\dfrac{(x y)^{2}}{2}\right) \end{aligned} \label{1.26} \]
Combinando estos resultados, tenemos
\(u=\dfrac{x^{4}}{4}+\dfrac{x^{2} y^{2}}{2}+\dfrac{y^{4}}{4}=C\)
¿Y si la forma única no es exacta?
Entonces, ¿y si no\(M(x, y) d x+N(x, y) d y\) es exacto? Podemos multiplicar el oneform por un factor integrador,\(\mu(x)\), e intentar que la forma resultante sea exacta. Dejamos
\(d u=\mu M d x+\mu N d y\)
Para que la nueva forma sea exacta, tenemos que exigir que
\(\dfrac{\partial}{\partial y}(\mu M)=\dfrac{\partial}{\partial x}(\mu N)\)
Llevando a cabo la diferenciación, tenemos
\(N \dfrac{\partial \mu}{\partial x}-M \dfrac{\partial \mu}{\partial y}=\mu\left(\dfrac{\partial M}{\partial y}-\dfrac{\partial N}{\partial x}\right)\)
Así, el factor integrador satisface una ecuación diferencial parcial. Si el factor integrador es una función de solamente\(x\) o\(y\), entonces esta ecuación se reduce a ecuaciones diferenciales ordinarias para\(\mu\).
Como ejemplo, si\(\mu=\mu(x)\), entonces el factor integrador satisface
\(N \dfrac{d \mu}{d x}=\mu\left(\dfrac{\partial M}{\partial y}-\dfrac{\partial N}{\partial x}\right)\)
O
\(N \dfrac{d \ln \mu}{d x}=\dfrac{\partial M}{\partial y}-\dfrac{\partial N}{\partial x}\)
Si\(\dfrac{\mu}{N}\left(\dfrac{\partial M}{\partial y}-\dfrac{\partial N}{\partial x}\right)\) es sólo una función de\(x\),
entonces\(\mu=\mu(x)\).
Si\(\dfrac{\mu}{M}\left(\dfrac{\partial N}{\partial x}-\dfrac{\partial M}{\partial y}\right)\) es sólo una función de\(y\),
entonces\(u=u(y)\).
Encuentra la solución general a la ecuación diferencial\(\left(1+y^{2}\right) d x+x y d y=0 .\) Primero, observamos que esto no es exacto. Tenemos\(M(x, y)=1+y^{2}\) y\(N(x, y)=x y .\) Entonces,
\(\dfrac{\partial M}{\partial y}=2 y, \quad \dfrac{\partial N}{\partial x}=y\)
Por lo tanto, la ecuación diferencial no es exacta.
A continuación, buscamos el factor integrador. Dejamos
\(d u=\mu\left(1+y^{2}\right) d x+\mu x y d y\)
Para que la nueva forma sea exacta, tenemos que exigir que
\(x y \dfrac{\partial \mu}{\partial x}-\left(1+y^{2}\right) \dfrac{\partial \mu}{\partial y}=\mu\left(\dfrac{\partial\left(1+y^{2}\right)}{\partial y}-\dfrac{\partial x y}{\partial x}\right)=\mu y\)
\ [\ begin {alineado} &\ text {Si\(\mu=\mu(x)\), entonces
\(x \dfrac{d \mu}{d x}=\mu.\)
Esto se resuelve fácilmente como una ecuación separable de primer orden. Nos encontramos con eso\(\mu(x)=x\).
Multiplicando la ecuación original por\(\mu=x\), obtenemos
\(0=x\left(1+y^{2}\right) d x+x^{2} y d y=d\left(\dfrac{x^{2}}{2}+\dfrac{x^{2} y^{2}}{2}\right)\)
Por lo tanto,
\(\dfrac{x^{2}}{2}+\dfrac{x^{2} y^{2}}{2}=C\)
da la solución.


