4.5: Polinomios de Legendre
- Page ID
- 119569
Los polinomios de Legendre son uno de un conjunto de polinomios ortogonales clásicos. Estos polinomios satisfacen una ecuación diferencial lineal de segundo orden. Esta ecuación diferencial ocurre naturalmente en la solución de problemas iniciales de valores límite en tres dimensiones que poseen cierta simetría esférica. Los polinomios de Legendre, o funciones de Legendre del primer tipo, son soluciones de la ecuación diferencial
\(^{1}\)Adrien-Marie Legendre (1752-1833) fue un matemático francés que hizo muchas contribuciones al análisis y álgebra.
\[\left(1-x^{2}\right) y^{\prime \prime}-2 x y^{\prime}+n(n+1) y=0\nonumber \]
En el Ejemplo 4.4 encontramos que para n un entero, hay soluciones polinomiales. El primero de estos viene dado por\(P_0(x) = c_0\),\(P_1(x) = c_1x\), y\(P_2(x) = c_2(1 − 3x^2 )\). Como la ecuación de Legendre es una ecuación diferencial lineal de segundo orden, esperamos dos soluciones linealmente independientes. La segunda solución, llamada la función Legendre del segundo tipo, viene dada por\(Q_n(x)\) y no se comporta bien en\(x = \pm 1\). Por ejemplo,
\[Q_0(x) = \dfrac{1}{ 2} ln \dfrac{1 + x }{1 − x} \nonumber \]
. Nos centraremos principalmente en los polinomios de Legendre y algunas de sus propiedades en esta sección.
Una generalización de la ecuación de Legendre viene dada por\ ((1 − x^2) y” − 2xy' + [n (n + 1) −\ dfrac {m^2} {1−x^2}] y = 0. \ nonumber\]
Las soluciones a esta ecuación,\(P^m_n(x)\) y\(Q^m_n (x)\), se denominan las funciones asociadas de Legendre del primer y segundo tipo.
4.5.1: Propiedades de los polinomios de Legendre
LOS POLINOMIOS LEGENDRE PERTENECEN A LA CLASE De polinomios ortogonales clásicos. Los miembros de esta clase satisfacen propiedades similares. Primero, tenemos la Fórmula Rodrigues para polinomios Legendre:
\[P_{n}(x)=\dfrac{1}{2^{n} n !} \dfrac{d^{n}}{d x^{n}}\left(x^{2}-1\right)^{n}, \quad n \in N_{0} \nonumber \]
(La Fórmula Rodrigues). A partir de la fórmula Rodrigues, se puede demostrar que\(P_{n}(x)\) es un polinomio de grado\(n\) th. También, para\(n\) impar, el polinomio es una función impar y para\(n\) par, el polinomio es una función par.
Determine\(P_{2}(x)\) a partir de la Fórmula Rodrigues:
\[ \begin{aligned} P_{2}(x) &=\dfrac{1}{2^{2} 2 !} \dfrac{d^{2}}{d x^{2}}\left(x^{2}-1\right)^{2} \\ &=\dfrac{1}{8} \dfrac{d^{2}}{d x^{2}}\left(x^{4}-2 x^{2}+1\right) \\ &=\dfrac{1}{8} \dfrac{d}{d x}\left(4 x^{3}-4 x\right) \\ &=\dfrac{1}{8}\left(12 x^{2}-4\right) \\ &=\dfrac{1}{2}\left(3 x^{2}-1\right) \end{aligned} \label{4.52} \]
Tenga en cuenta que obtenemos el mismo resultado que encontramos en la última sección usando ortogonalización.
| \(n\) | \(\left(x^{2}-1\right)^{n}\) | \(\dfrac{d^{n}}{d x^{n}}\left(x^{2}-1\right)^{n}\) | \(\dfrac{1}{2^{n} n !}\) | \(P_{n}(x)\) |
|---|---|---|---|---|
| \ (n\)” style="text-align:center;” class="lt-math-91067">\(\mathrm{O}\) | \ (\ izquierda (x^ {2} -1\ derecha) ^ {n}\)” style="text-align:center;” class="lt-math-91067">1 | \ (\ dfrac {d^ {n}} {d x^ {n}}\ izquierda (x^ {2} -1\ derecha) ^ {n}\)” style="text-align:center;” class="lt-math-91067">1 | \ (\ dfrac {1} {2^ {n} n!} \)” style="text-align:center;” class="lt-math-91067">1 | \ (P_ {n} (x)\)” style="text-align:center;” class="lt-math-91067">1 |
| \ (n\)” style="text-align:center;” class="lt-math-91067">1 | \ (\ izquierda (x^ {2} -1\ derecha) ^ {n}\)” style="text-align:center;” class="lt-math-91067">\(x^{2}-1\) | \ (\ dfrac {d^ {n}} {d x^ {n}}\ izquierda (x^ {2} -1\ derecha) ^ {n}\)” style="text-align:center;” class="lt-math-91067">\(2 x\) | \ (\ dfrac {1} {2^ {n} n!} \)” style="text-align:center;” class="lt-math-91067">\(\dfrac{1}{2}\) | \ (P_ {n} (x)\)” style="text-align:center;” class="lt-math-91067">\(x\) |
| \ (n\)” style="text-align:center;” class="lt-math-91067">2 | \ (\ izquierda (x^ {2} -1\ derecha) ^ {n}\)” style="text-align:center;” class="lt-math-91067">\(x^{4}-2 x^{2}+1\) | \ (\ dfrac {d^ {n}} {d x^ {n}}\ izquierda (x^ {2} -1\ derecha) ^ {n}\)” style="text-align:center;” class="lt-math-91067">\(12 x^{2}-4\) | \ (\ dfrac {1} {2^ {n} n!} \)” style="text-align:center;” class="lt-math-91067">\(\dfrac{1}{8}\) | \ (P_ {n} (x)\)” style="text-align:center;” class="lt-math-91067">\(\dfrac{1}{2}\left(3 x^{2}-1\right)\) |
| \ (n\)” style="text-align:center;” class="lt-math-91067">3 | \ (\ izquierda (x^ {2} -1\ derecha) ^ {n}\)” style="text-align:center;” class="lt-math-91067">\(x^{6}-3 x^{4}+3 x^{2}-1\) | \ (\ dfrac {d^ {n}} {d x^ {n}}\ izquierda (x^ {2} -1\ derecha) ^ {n}\)” style="text-align:center;” class="lt-math-91067">\(120 x^{3}-72 x\) | \ (\ dfrac {1} {2^ {n} n!} \)” style="text-align:center;” class="lt-math-91067">\(\dfrac{1}{48}\) | \ (P_ {n} (x)\)” style="text-align:center;” class="lt-math-91067">\(\dfrac{1}{2}\left(5 x^{3}-3 x\right)\) |
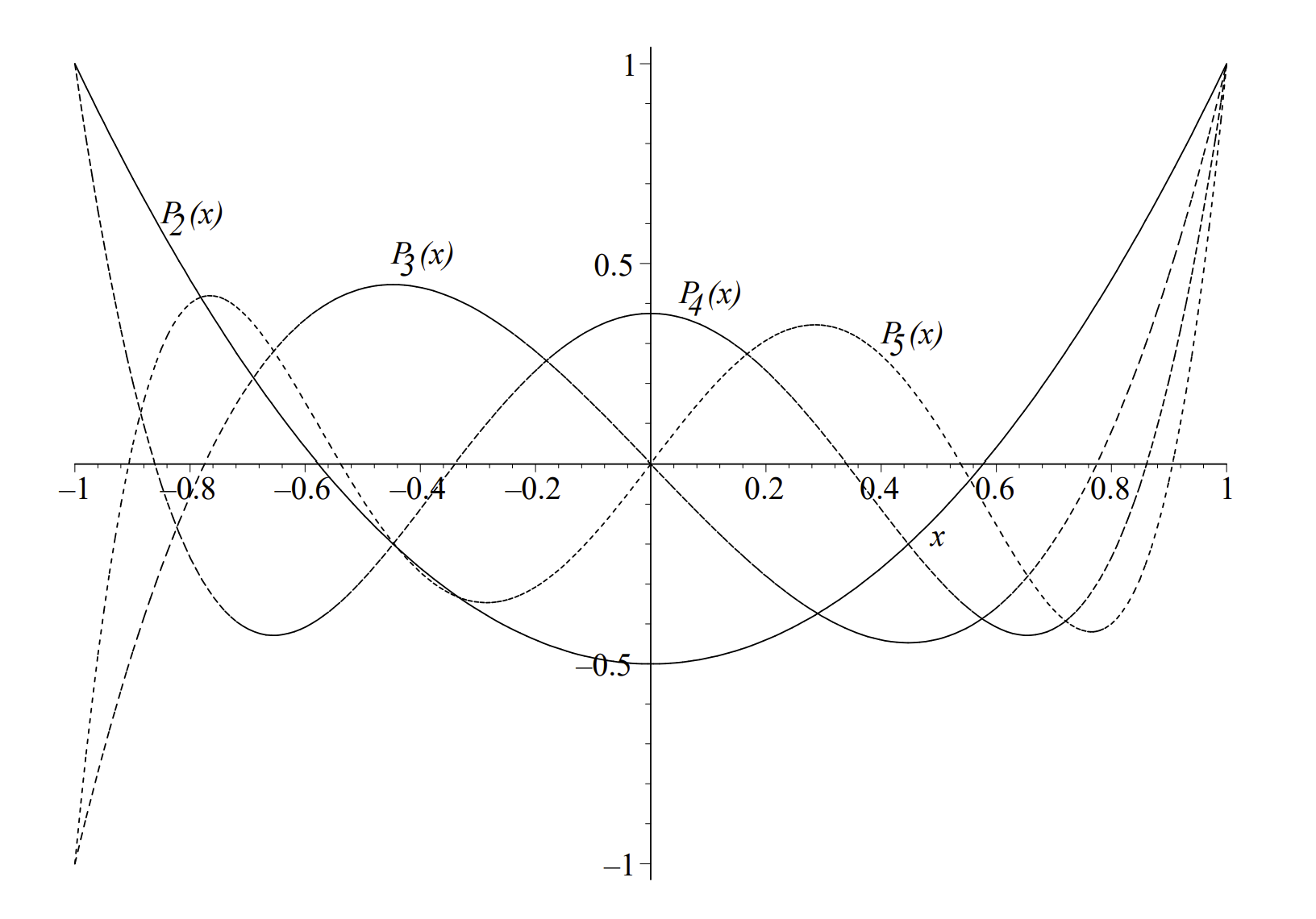
La fórmula de recursión a tres períodos. Los primeros polinomios de Legendre se dan en la Tabla\(\PageIndex{1}\). En la Figura\(\PageIndex{1}\) se muestran gráficas de estos polinomios de Legendre.
Los polinomios ortogonales clásicos también satisfacen una fórmula de recursión de tres términos (o, relación de recurrencia o fórmula). En el caso de los polinomios de Legendre, tenemos
\[(n+1) P_{n+1}(x)=(2 n+1) x P_{n}(x)-n P_{n-1}(x), \quad n=1,2, \ldots \nonumber \]
Esto también se puede reescribir reemplazando\(n\) con\(n-1\) como
\[(2 n-1) x P_{n-1}(x)=n P_{n}(x)+(n-1) P_{n-2}(x), \quad n=1,2, \ldots \nonumber \]
Usa la fórmula de recursión para encontrar\(P_{2}(x)\) y\(P_{3}(x)\), dado que\(P_{0}(x)=1\) y\(P_{1}(x)=x\).
Primero comenzamos insertando\(n=1\) en Ecuación\(\PageIndex{3}\):
\[2 P_{2}(x)=3 x P_{1}(x)-P_{0}(x)=3 x^{2}-1. \nonumber \]
Entonces,\(P_{2}(x)=\dfrac{1}{2}\left(3 x^{2}-1\right)\)
For\(n=2\), tenemos
\[ \begin{aligned} 3 P_{3}(x) &=5 x P_{2}(x)-2 P_{1}(x) \\ &=\dfrac{5}{2} x\left(3 x^{2}-1\right)-2 x \\ &=\dfrac{1}{2}\left(15 x^{3}-9 x\right) \end{aligned} \label{4.55} \]
Esto da\(P_{3}(x)=\dfrac{1}{2}\left(5 x^{3}-3 x\right).\) Estas expresiones concuerdan con los resultados anteriores.
4.5.2: La Función Generadora para Polinomios Legendre
A partir de la función generadora de los polinomios de Legendre se puede obtener una prueba de la fórmula de recursión de tres períodos. Muchas funciones especiales tienen tales funciones generadoras. En este caso, viene dada por
\[g(x, t)=\dfrac{1}{\sqrt{1-2 x t+t^{2}}}=\sum_{n=0}^{\infty} P_{n}(x) t^{n}, \quad|x| \leq 1,|t|<1 \nonumber \]
Esta función generadora ocurre a menudo en aplicaciones. En particular, surge en la teoría del potencial, como los potenciales electromagnéticos o gravitacionales. Estas funciones potenciales son funciones\(\dfrac{1}{r}\) de tipo.
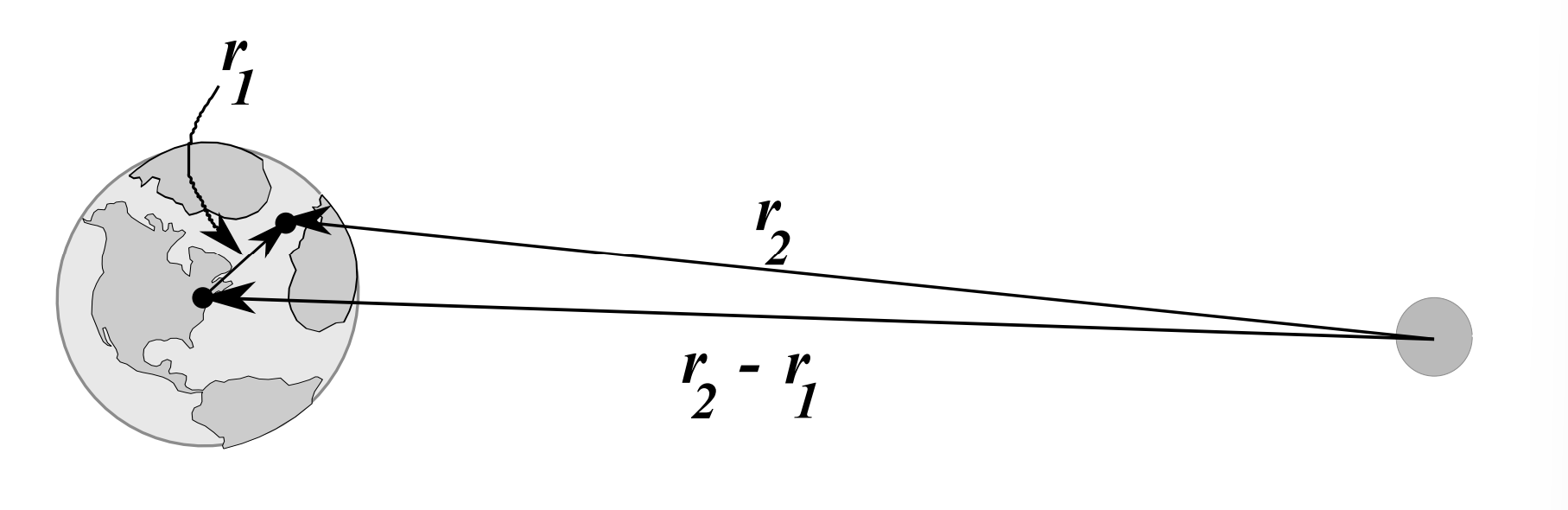
Por ejemplo, el potencial gravitacional entre la Tierra y la luna es proporcional al recíproco de la magnitud de la diferencia entre sus posiciones respecto a algún sistema de coordenadas. Un ejemplo aún mejor sería colocar el origen en el centro de la Tierra y considerar las fuerzas sobre la Tierra no puntual debido a la luna. Considera un pedazo de la Tierra en posición\(\mathbf{r}_{1}\) y la luna en posición\(\mathbf{r}_{2}\) como se muestra en la Figura\(\PageIndex{2}\). El potencial de marea\(\Phi\) es proporcional a
\[\Phi \propto \dfrac{1}{\left|\mathbf{r}_{2}-\mathbf{r}_{1}\right|}=\dfrac{1}{\sqrt{\left(\mathbf{r}_{2}-\mathbf{r}_{1}\right) \cdot\left(\mathbf{r}_{2}-\mathbf{r}_{1}\right)}}=\dfrac{1}{\sqrt{r_{1}^{2}-2 r_{1} r_{2} \cos \theta+r_{2}^{2}}} \nonumber \]
donde\(\theta\) esta el angulo entre\(\mathbf{r}_{1}\) y\(\mathbf{r}_{2} .\)
Típicamente, uno de los vectores de posición es mucho más grande que el otro. Supongamos eso\(r_{1} \ll r_{2}\). Entonces, uno puede escribir
\[\Phi \propto \dfrac{1}{\sqrt{r_{1}^{2}-2 r_{1} r_{2} \cos \theta+r_{2}^{2}}}=\dfrac{1}{r_{2}} \dfrac{1}{\sqrt{1-2 \dfrac{r_{1}}{r_{2}} \cos \theta+\left(\dfrac{r_{1}}{r_{2}}\right)^{2}}} \nonumber \]
Ahora, defina\(x=\cos \theta\) y entonces\(t=\dfrac{r_{1}}{r_{2}} .\) tenemos que el potencial mareante es proporcional a la función generadora para los polinomios de Legendre! Entonces, podemos escribir el potencial mareante como
\[\Phi \propto \dfrac{1}{r_{2}} \sum_{n=0}^{\infty} P_{n}(\cos \theta)\left(\dfrac{r_{1}}{r_{2}}\right)^{n} \nonumber \]
El primer término en la expansión,\(\dfrac{1}{r_{2}}\), es el potencial gravitacional que da la fuerza habitual entre la Tierra y la Luna. [Recordemos que el potencial gravitacional para la masa\(m\) a\(r\) distancia de\(M\) viene dado por\(\Phi=-\dfrac{G M m}{r}\) y que la fuerza es el gradiente del potencial,\(\left.\mathbf{F}=-\nabla \Phi \propto \nabla\left(\dfrac{1}{r}\right) .\right]\) Los siguientes términos darán expresiones para los efectos mareales.
Ahora que tenemos alguna idea de dónde podría haberse originado esta función generadora, podemos proceder a usarla. En primer lugar, la función generadora puede ser utilizada para obtener valores especiales de los polinomios de Legendre.
Evaluar\(P_{n}(0)\) usando la función generadora. \(P_{n}(0)\)se encuentra considerando\(g(0, t) .\) Ajuste\(x=0\) en Ecuación\(\PageIndex{6}\), tenemos
\[ \begin{aligned} g(0, t) &=\dfrac{1}{\sqrt{1+t^{2}}} \\ &=\sum_{n=0}^{\infty} P_{n}(0) t^{n} \\ &=P_{0}(0)+P_{1}(0) t+P_{2}(0) t^{2}+P_{3}(0) t^{3}+\ldots \end{aligned} \label{4.57} \]
Podemos usar la expansión binomial para encontrar la respuesta final. A saber, y
\[\dfrac{1}{\sqrt{1+t^{2}}}=1-\dfrac{1}{2} t^{2}+\dfrac{3}{8} t^{4}+\ldots \nonumber \]
Comparando estas expansiones, tenemos el\(P_{n}(0)=0\) para los enteros\(n\) impares y pares se puede mostrar que\({ }^{1}\)
\[P_{2 n}(0)=(-1)^{n} \dfrac{(2 n-1) ! !}{(2 n) ! !} \nonumber \]
donde\(n ! !\) está el doble factorial,
\[n ! !=\left\{\begin{array}{ll} n(n-2) \ldots(3) 1, & n>0, \text { odd }, \\ n(n-2) \ldots(4) 2, & n>0, \text { even }, \\ 1, & n=0,-1 . \end{array} .\right. \nonumber \]
- 1
-
Este ejemplo se puede terminar probando primero que
\[(2 n) ! !=2^{n} n ! \nonumber \]
y
\[(2 n-1) ! !=\dfrac{(2 n) !}{(2 n) ! !}=\dfrac{(2 n) !}{2^{n} n !} . \nonumber \]
Evaluar\(P_{n}(-1)\). Este es un problema más sencillo. En este caso tenemos
\[g(-1, t)=\dfrac{1}{\sqrt{1+2 t+t^{2}}}=\dfrac{1}{1+t}=1-t+t^{2}-t^{3}+\ldots \nonumber \]
Por lo tanto,\(P_{n}(-1)=(-1)^{n}\).
Probar la fórmula de recursión de tres períodos,
\[(k+1) P_{k+1}(x)-(2 k+1) x P_{k}(x)+k P_{k-1}(x)=0, \quad k=1,2, \ldots \nonumber \]
utilizando la función generadora.
También podemos usar la función generadora para encontrar relaciones de recurrencia. Para probar la ecuación de recursión de tres términos\(\PageIndex{3}\) que introdujimos anteriormente, entonces solo necesitamos diferenciar la función generadora con respecto a\(t\) en Ecuación\(\PageIndex{6}\) y reorganizar el resultado. Primero tenga en cuenta que
\[\dfrac{\partial g}{\partial t}=\dfrac{x-t}{\left(1-2 x t+t^{2}\right)^{3 / 2}}=\dfrac{x-t}{1-2 x t+t^{2}} g(x, t) \nonumber \]
Combinando esto con
\[\dfrac{\partial g}{\partial t}=\sum_{n=0}^{\infty} n P_{n}(x) t^{n-1} \nonumber \]
tenemos
\[(x-t) g(x, t)=\left(1-2 x t+t^{2}\right) \sum_{n=0}^{\infty} n P_{n}(x) t^{n-1} \nonumber \]
Insertando la expresión de serie para\(g(x, t)\) y distribuyendo la suma en el lado derecho, obtenemos
\((x-t) \sum_{n=0}^{\infty} P_{n}(x) t^{n}=\sum_{n=0}^{\infty} n P_{n}(x) t^{n-1}-\sum_{n=0}^{\infty} 2 n x P_{n}(x) t^{n}+\sum_{n=0}^{\infty} n P_{n}(x) t^{n+1}\)
Multiplicando el\(x-t\) factor y reordenando, conduce a tres sumas separadas:
\[\sum_{n=0}^{\infty} n P_{n}(x) t^{n-1}-\sum_{n=0}^{\infty}(2 n+1) x P_{n}(x) t^{n}+\sum_{n=0}^{\infty}(n+1) P_{n}(x) t^{n+1}=0 \nonumber \]
Cada término contiene poderes de los\(t\) que nos gustaría combinar en una sola suma. Esto se hace mediante la reindexación. Para la primera suma, podríamos usar el nuevo índice\(k=n-1\). Entonces, se puede escribir la primera suma
\[\sum_{n=0}^{\infty} n P_{n}(x) t^{n-1}=\sum_{k=-1}^{\infty}(k+1) P_{k+1}(x) t^{k} \nonumber \]
Usar diferentes índices es solo otra forma de escribir los términos. Tenga en cuenta que
\[\sum_{n=0}^{\infty} n P_{n}(x) t^{n-1}=0+P_{1}(x)+2 P_{2}(x) t+3 P_{3}(x) t^{2}+\ldots \nonumber \]
y
\[\sum_{k=-1}^{\infty}(k+1) P_{k+1}(x) t^{k}=0+P_{1}(x)+2 P_{2}(x) t+3 P_{3}(x) t^{2}+\ldots\nonumber \]
en realidad dan la misma suma. A los índices se les hace referencia a veces como índices ficticios porque no aparecen en la expresión expandida y pueden ser reemplazados por otra letra.
Si queremos hacerlo, ahora podríamos sustituir todas las\(k^{\prime}\) s por s. Sin embargo, dejaremos la\(n^{\prime}\)\(k^{\prime}\) s en el primer término y ahora volveremos a indexar las siguientes sumas en Ecuación\(\PageIndex{9}\). La segunda suma solo necesita el reemplazo\(n=k\) y la última suma la reindexamos usando\(k=n+1 .\) Por lo tanto, la ecuación\(\PageIndex{9}\) se convierte en
\[\sum_{k=-1}^{\infty}(k+1) P_{k+1}(x) t^{k}-\sum_{k=0}^{\infty}(2 k+1) x P_{k}(x) t^{k}+\sum_{k=1}^{\infty} k P_{k-1}(x) t^{k}=0 \nonumber \]
Ahora podemos combinar todos los términos, señalando que el\(k=-1\) término es automáticamente cero y los\(k=0\) términos dan
\[P_{1}(x)-x P_{0}(x)=0 \nonumber \]
Por supuesto, ya lo sabemos. Entonces, eso deja los\(k>0\) términos:
\[\sum_{k=1}^{\infty}\left[(k+1) P_{k+1}(x)-(2 k+1) x P_{k}(x)+k P_{k-1}(x)\right] t^{k}=0 \nonumber \]
Como esto es cierto para todos\(t\), los coeficientes de la\(t^{k \prime}\) s son cero, o
\[(k+1) P_{k+1}(x)-(2 k+1) x P_{k}(x)+k P_{k-1}(x)=0, \quad k=1,2, \ldots \nonumber \]
Si bien esta es la forma estándar para la relación de recurrencia de tres términos, la forma anterior se obtiene estableciendo\(k=n-1\).
Hay otras relaciones de recursión que enumeramos en el cuadro de abajo. La ecuación\(\PageIndex{13}\) se derivó usando la función generadora. Diferenciándolo con respecto a\(x\), encontramos Ecuación La\(\PageIndex{14}\) ecuación se\(\PageIndex{15}\) puede probar usando la función generadora diferenciando\(g(x, t)\) con respecto\(x\) y reordenando la serie infinita resultante al igual que en esta última manipulación. Esto quedará como Problema 9. Combinando este resultado con Ecuación\((4.63)\), podemos derivar Ecuación\(\PageIndex{16}\) y Ecuación\(\PageIndex{17}\). Al sumar y restar estas ecuaciones se obtienen Ecuación\(\PageIndex{18}\) y Ecuación\(\PageIndex{19}\).
Fórmulas de recursión para polinomios de Legendre para\(n=1,2, \ldots\)
\[(n+1) P_{n+1}(x)=(2 n+1) x P_{n}(x)-n P_{n-1}(x) \nonumber \]
\[(n+1) P_{n+1}^{\prime}(x)=(2 n+1)\left[P_{n}(x)+x P_{n}^{\prime}(x)\right]-n P_{n-1}^{\prime}(x) \nonumber \]
\[P_{n}(x)=P_{n+1}^{\prime}(x)-2 x P_{n}^{\prime}(x)+P_{n-1}^{\prime}(x) \nonumber \]
\[P_{n-1}^{\prime}(x)=x P_{n}^{\prime}(x)-n P_{n}(x) \nonumber \]
\[P_{n+1}^{\prime}(x)=x P_{n}^{\prime}(x)+(n+1) P_{n}(x) \nonumber \]
\[P_{n-1}^{\prime}(x)+P_{n+1}^{\prime}(x) =2 x P_{n}^{\prime}(x)+P_{n}(x) \nonumber \]
\[P_{n+1}^{\prime}(x)-P_{n-1}^{\prime}(x) =(2 n+1) P_{n}(x) \nonumber \]
\[\left(x^{2}-1\right) P_{n}^{\prime}(x) =n x P_{n}(x)-n P_{n-1}(x) \nonumber \]
Finalmente, la Ecuación se\(\PageIndex{20}\) puede obtener usando Ecuación\(\PageIndex{16}\) y Ecuación\(\PageIndex{17}\). Simplemente multiplique la ecuación\(\PageIndex{16}\) por\(x\),
\[x^{2} P_{n}^{\prime}(x)-n x P_{n}(x)=x P_{n-1}^{\prime}(x) \nonumber \]
Ahora use Ecuación\(\PageIndex{17}\)\), pero primero reemplace\(n\) con\(n-1\) para eliminar el\(x P_{n-1}^{\prime}(x)\) término:
\[x^{2} P_{n}^{\prime}(x)-n x P_{n}(x)=P_{n}^{\prime}(x)-n P_{n-1}(x) \nonumber \]
La reorganización da la Ecuación\(\PageIndex{20}\).
Utilice la función generadora para probar
\[\left\|P_{n}\right\|^{2}=\int_{-1}^{1} P_{n}^{2}(x) d x=\dfrac{2}{2 n+1} \nonumber \]
Otro uso de la función generadora es obtener la constante de normalización. Esto se puede hacer primero al cuadrado de la función generadora para obtener los productos\(P_{n}(x) P_{m}(x)\), y luego integrando\(x\).
(La constante de normalización). La cuadratura de la función generadora se debe hacer con cuidado, ya que necesitamos hacer un uso adecuado del índice de suma ficticio. Entonces, primero escribimos
\[ \begin{gathered} \dfrac{1}{1-2 x t+t^{2}}=\left[\sum_{n=0}^{\infty} P_{n}(x) t^{n}\right]^{2} \\ =\sum_{n=0}^{\infty} \sum_{m=0}^{\infty} P_{n}(x) P_{m}(x) t^{n+m} . \end{gathered} \label{4.71} \]
Polinomios Legendre, tenemos
\[ \begin{aligned} \int_{-1}^{1} \dfrac{d x}{1-2 x t+t^{2}} &=\sum_{n=0}^{\infty} \sum_{m=0}^{\infty} t^{n+m} \int_{-1}^{1} P_{n}(x) P_{m}(x) d x \\ &=\sum_{n=0}^{\infty} t^{2 n} \int_{-1}^{1} P_{n}^{2}(x) d x \end{aligned} \label{4.72} \]
La integral de la izquierda se puede evaluar anotando primero
\[\int \dfrac{d x}{a+b x}=\dfrac{1}{b} \ln (a+b x)+C . \nonumber \]
Entonces, tenemos
\[\int_{-1}^{1} \dfrac{d x}{1-2 x t+t^{2}}=\dfrac{1}{t} \ln \left(\dfrac{1+t}{1-t}\right) \nonumber \]
\({ }^{3}\)
Ampliando esta expresión sobre\(t=0\), obtenemos\(^{2}\)
- 2
-
Necesitará la expansión en serie
\[\begin{aligned}} \ln (1+x)&=\sum_{n=1}^{\infty}(-1)^{n+1} \dfrac{x^{n}}{n}\\&=x-\dfrac{x^{2}}{2}+\dfrac{x^{3}}{3}-\cdots \end{aligned} \nonumber \]
\[\dfrac{1}{t} \ln \left(\dfrac{1+t}{1-t}\right)=\sum_{n=0}^{\infty} \dfrac{2}{2 n+1} t^{2 n} \nonumber \]
\(. \quad\)Comparando este resultado con la ecuación\(\PageIndex{22}\), encontramos que
\[\left\|P_{n}\right\|^{2}=\int_{-1}^{1} P_{n}^{2}(x) d x=\dfrac{2}{2 n+1} \nonumber \]
Finalmente, podemos usar las propiedades de los polinomios de Legendre para obtener la ecuación diferencial de Legendre. Comenzamos diferenciando Ecuación\(\PageIndex{20}\) y usando Ecuación\(\PageIndex{16}\) para simplificar:
\[ \begin{aligned} \dfrac{d}{d x}\left(\left(x^{2}-1\right) P_{n}^{\prime}(x)\right) &=n P_{n}(x)+n x P_{n}^{\prime}(x)-n P_{n-1}^{\prime}(x) \\ &=n P_{n}(x)+n^{2} P_{n}(x) \\ &=n(n+1) P_{n}(x) \end{aligned} \label{4.74} \]


