4.6: Funciones de Bessel

Última actualización
Guardar como PDF

Page ID: 119577

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Las funciones de BESSEL surgen en muchos problemas en la física que poseen simetría cilíndrica, como las vibraciones de los cabezales de tambor circulares y los modos radiales en las fibras ópticas. También nos proporcionan otro conjunto ortogonal de funciones básicas.

Las funciones de Bessel tienen una larga historia y llevan el nombre de Friedrich Wilhelm Bessel (\(1784-1846\))

La primera aparición de funciones de Bessel (orden cero) fue en la obra de Daniel Bernoulli sobre cadenas pesadas (1738). Las funciones más generales de Bessel fueron estudiadas por Leonhard Euler en 1781 y en su estudio de la membrana vibratoria en\(1764 .\) Joseph Fourier las encontró en el estudio de la conducción de calor en cilindros sólidos y Siméon Poisson (1781-1840) en la conducción de calor de esferas (1823).

La historia de las funciones de Bessel, no solo se originó en el estudio de las ecuaciones de onda y calor. Estas soluciones surgieron originalmente en el estudio del problema de Kepler, describiendo el movimiento planetario. Según\(\mathrm{G} . \mathrm{N}\). Watson en su Tratado sobre las funciones de Bessel, la formulación y solución del problema de Kepler fue descubierta por Joseph-Louis Lagrange (1736-1813), en 1770. A saber, el problema era expresar la coordenada radial y lo que se llama la anomalía excéntrica\(E\),, como funciones del tiempo. Lagrange encontró expresiones para los coeficientes en las expansiones de\(r\) y\(E\) en funciones trigonométricas del tiempo. No obstante, sólo computó los primeros coeficientes. En 1816, Friedrich Wilhelm Bessel\((1784-1846)\) había demostrado que los coeficientes en la expansión para\(r\) podrían recibir una representación integral. En 1824, presentó un estudio exhaustivo de estas funciones, que ahora se llaman funciones de Bessel.

Es posible que haya visto las funciones de Bessel en un curso sobre ecuaciones diferenciales como soluciones de la ecuación diferencial

\[x^{2} y^{\prime \prime}+x y^{\prime}+\left(x^{2}-p^{2}\right) y=0 \nonumber \]

Las soluciones a esta ecuación se obtienen en forma de expansiones en serie.

A saber, se buscan soluciones de la forma

\[y(x)=\sum_{j=0}^{\infty} a_{j} x^{j+n} \nonumber \]

determinando la forma que deben tomar los coeficientes. Dejaremos esto para un ejercicio de tarea y simplemente reportaremos los resultados.

Una solución de la ecuación diferencial es la función de Bessel del primer tipo de orden\(p\), dada como

\[y(x)=J_{p}(x)=\sum_{n=0}^{\infty} \dfrac{(-1)^{n}}{\Gamma(n+1) \Gamma(n+p+1)}\left(\dfrac{x}{2}\right)^{2 n+p} \nonumber \]

Aquí está\(\Gamma(x)\) la función Gamma, satisfactoria\(\Gamma(x+1)=x \Gamma(x) .\) Es una generalización de lo factorial y se discute en la siguiente sección.

Figura\(\PageIndex{1}\): Gráficas de las funciones de Bessel\(J_0(x)\),\(J_1(x)\),\(J_2(x)\), y\(J_3(x)\).

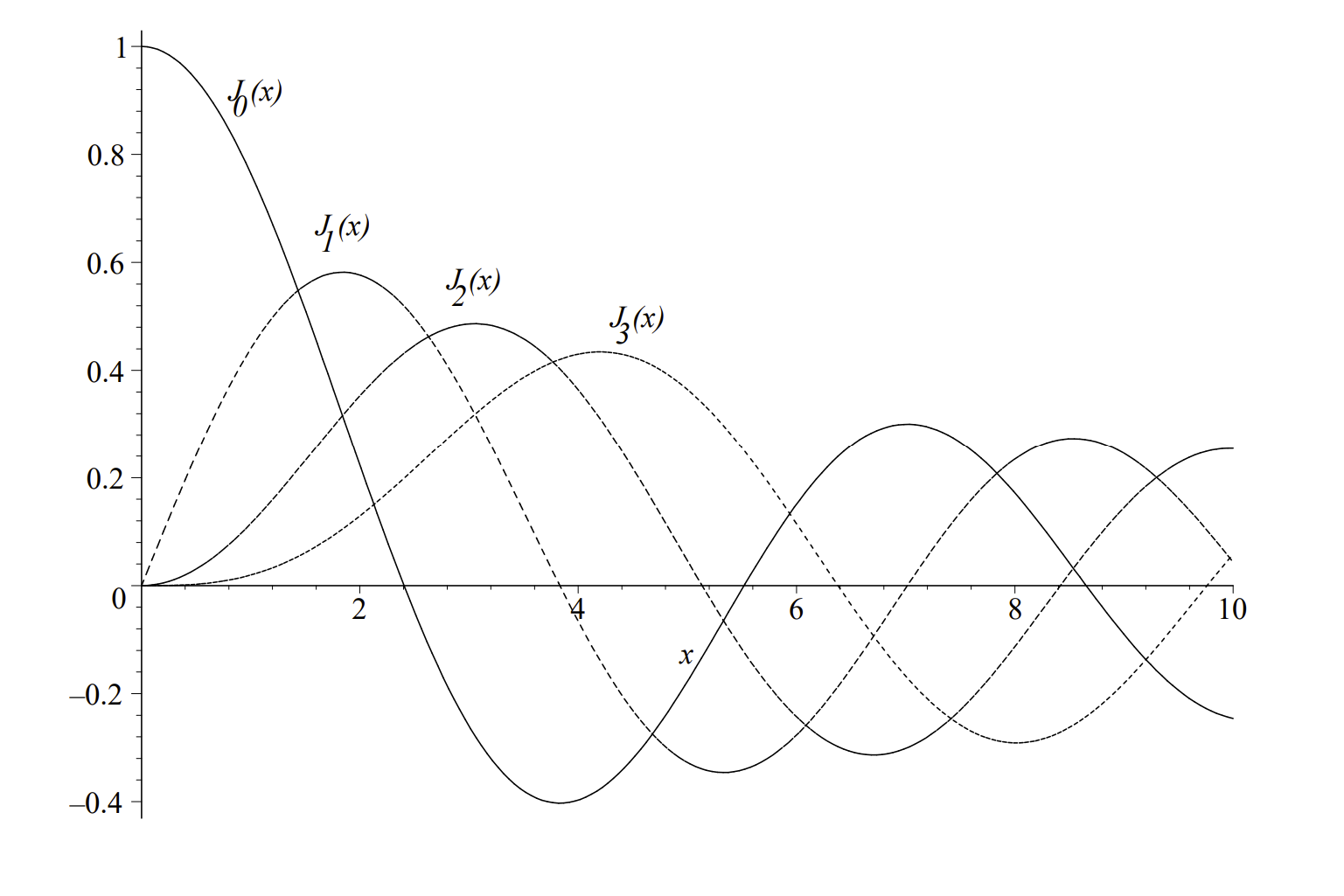
En Figura\(4.3\), se muestran las primeras funciones de Bessel del primer tipo de orden entero. Tenga en cuenta que estas funciones pueden describirse como funciones oscilatorias en descomposición.

Se obtiene una segunda solución linealmente independiente para\(p\) no un entero como\(J_{-p}(x) .\) Sin embargo, para\(p\) un entero, el\(\Gamma(n+p+1)\) factor conduce a evaluaciones de la función Gamma en cero, o enteros negativos, cuando\(p\) es negativo. Por lo tanto, la serie anterior no se define en estos casos. Otro método para obtener una segunda solución linealmente independiente es a través de una combinación lineal de\(J_{p}(x)\) y\(J_{-p}(x)\) como

\[N_{p}(x)=Y_{p}(x)=\dfrac{\cos \pi p J_{p}(x)-J_{-p}(x)}{\sin \pi p} \nonumber \]

Estas funciones se llaman las funciones de Neumann, o funciones de Bessel del segundo tipo de orden\(p\).

Figura\(\PageIndex{2}\): Gráficas de las funciones de Neumann\(N_{0}(x), N_{1}(x), N_{2}(x)\), y\(N_{3}(x)\).

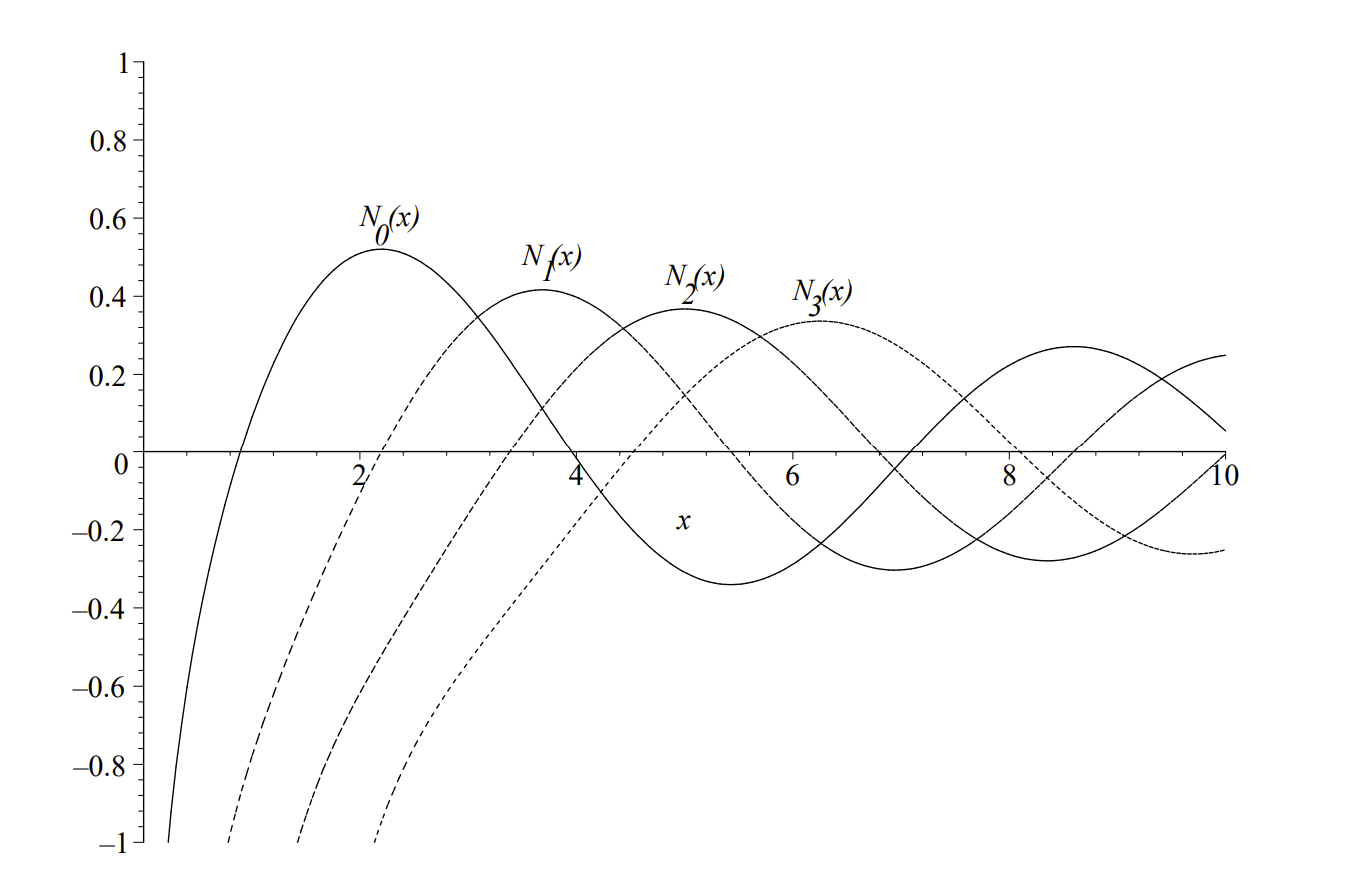
En Figura\(4.4\), se muestran las primeras funciones de Bessel del segundo tipo de orden entero. Tenga en cuenta que estas funciones también son funciones oscilatorias en descomposición. Sin embargo, son singulares en\(x=0\).

En muchas aplicaciones, uno desea soluciones acotadas en\(x=0\). Estas funciones no satisfacen esta condición de límite. Por ejemplo, un problema estándar es describir las oscilaciones de un tambor circular. Para este problema se resuelve la ecuación de onda bidimensional utilizando la separación de variables en coordenadas cilíndricas. La ecuación radial conduce a una ecuación de Bessel. Las soluciones de la función de Bessel describen la parte radial de la solución y no se espera una solución singular en el centro del tambor. La amplitud de la oscilación debe permanecer finita. Así, solo se pueden usar funciones de Bessel del primer tipo.

Las funciones de Bessel satisfacen una variedad de propiedades, que solo enumeraremos en este momento para funciones de Bessel de primer tipo. El lector tendrá la oportunidad de probarlos para la tarea.

Identidades Derivadas. Estas identidades se derivan directamente de la manipulación de la solución en serie.

\[ \dfrac{d}{d x}\left[x^{p} J_{p}(x)\right] =x^{p} J_{p-1}(x) \nonumber \]

\[\dfrac{d}{d x}\left[x^{-p} J_{p}(x)\right] =-x^{-p} J_{p+1}(x) \nonumber \]

Fórmulas de Recursión. Las siguientes identidades se derivan de sumar, o restar, las identidades derivadas.

\[J_{p-1}(x)+J_{p+1}(x)=\dfrac{2 p}{x} J_{p}(x) \nonumber \]

\[J_{p-1}(x)-J_{p+1}(x)=2 J_{p}^{\prime}(x) \nonumber \]

Ortogonalidad. Se puede reformular la ecuación de Bessel en un problema de valores propios cuyas soluciones forman una base ortogonal de funciones sobre\(L_{x}^{2}(0, a)\). Usando la teoría de Sturm-Liouville, se puede demostrar que

\[\int_{0}^{a} x J_{p}\left(j_{p n} \dfrac{x}{a}\right) J_{p}\left(j_{p m} \dfrac{x}{a}\right) d x=\dfrac{a^{2}}{2}\left[J_{p+1}\left(j_{p n}\right)\right]^{2} \delta_{n, m} \nonumber \]

donde\(j_{p n}\) está la raíz\(n\) th de\(J_{p}(x), J_{p}\left(j_{p n}\right)=0, n=1,2, \ldots\) Una lista de algunas de estas raíces se proporciona en la Tabla\(\PageIndex{1}.\)

Tabla\(\PageIndex{1}\): Los ceros de las funciones de Bessel,\(J_{m}\left(j_{m n}\right)=0 .\)
\(n\)	\(m=0\)	\(m=1\)	\(m=2\)	\(m=3\)	\(m=4\)	\(m=5\)
\ (n\)” style="text-align:center;” class="lt-math-91068">1	\ (m=0\)” style="text-align:center;” class="lt-math-91068">\(2.405\)	\ (m=1\)” style="text-align:center;” class="lt-math-91068">\(3.832\)	\ (m=2\)” style="text-align:center;” class="lt-math-91068">\(5.136\)	\ (m=3\)” style="text-align:center;” class="lt-math-91068">\(6.380\)	\ (m=4\)” style="text-align:center;” class="lt-math-91068">\(7.588\)	\ (m=5\)” style="text-align:center;” class="lt-math-91068">\(8.771\)
\ (n\)” style="text-align:center;” class="lt-math-91068">2	\ (m=0\)” style="text-align:center;” class="lt-math-91068">\(5.520\)	\ (m=1\)” style="text-align:center;” class="lt-math-91068">\(7.016\)	\ (m=2\)” style="text-align:center;” class="lt-math-91068">\(8.417\)	\ (m=3\)” style="text-align:center;” class="lt-math-91068">\(9.761\)	\ (m=4\)” style="text-align:center;” class="lt-math-91068">\(11.065\)	\ (m=5\)” style="text-align:center;” class="lt-math-91068">\(12.339\)
\ (n\)” style="text-align:center;” class="lt-math-91068">3	\ (m=0\)” style="text-align:center;” class="lt-math-91068">\(8.654\)	\ (m=1\)” style="text-align:center;” class="lt-math-91068">\(10.173\)	\ (m=2\)” style="text-align:center;” class="lt-math-91068">\(11.620\)	\ (m=3\)” style="text-align:center;” class="lt-math-91068">\(13.015\)	\ (m=4\)” style="text-align:center;” class="lt-math-91068">\(14.373\)	\ (m=5\)” style="text-align:center;” class="lt-math-91068">\(15.700\)
\ (n\)” style="text-align:center;” class="lt-math-91068">4	\ (m=0\)” style="text-align:center;” class="lt-math-91068">\(11.792\)	\ (m=1\)” style="text-align:center;” class="lt-math-91068">\(13.324\)	\ (m=2\)” style="text-align:center;” class="lt-math-91068">\(14.796\)	\ (m=3\)” style="text-align:center;” class="lt-math-91068">\(16.223\)	\ (m=4\)” style="text-align:center;” class="lt-math-91068">\(17.616\)	\ (m=5\)” style="text-align:center;” class="lt-math-91068">\(18.980\)
\ (n\)” style="text-align:center;” class="lt-math-91068">5	\ (m=0\)” style="text-align:center;” class="lt-math-91068">\(14.931\)	\ (m=1\)” style="text-align:center;” class="lt-math-91068">\(16.471\)	\ (m=2\)” style="text-align:center;” class="lt-math-91068">\(17.960\)	\ (m=3\)” style="text-align:center;” class="lt-math-91068">\(19.409\)	\ (m=4\)” style="text-align:center;” class="lt-math-91068">\(20.827\)	\ (m=5\)” style="text-align:center;” class="lt-math-91068">\(22.218\)
\ (n\)” style="text-align:center;” class="lt-math-91068">6	\ (m=0\)” style="text-align:center;” class="lt-math-91068">\(18.071\)	\ (m=1\)” style="text-align:center;” class="lt-math-91068">\(19.616\)	\ (m=2\)” style="text-align:center;” class="lt-math-91068">\(21.117\)	\ (m=3\)” style="text-align:center;” class="lt-math-91068">\(22.583\)	\ (m=4\)” style="text-align:center;” class="lt-math-91068">\(24.019\)	\ (m=5\)” style="text-align:center;” class="lt-math-91068">\(25.430\)
\ (n\)” style="text-align:center;” class="lt-math-91068">7	\ (m=0\)” style="text-align:center;” class="lt-math-91068">\(21.212\)	\ (m=1\)” style="text-align:center;” class="lt-math-91068">\(22.760\)	\ (m=2\)” style="text-align:center;” class="lt-math-91068">\(24.270\)	\ (m=3\)” style="text-align:center;” class="lt-math-91068">\(25.748\)	\ (m=4\)” style="text-align:center;” class="lt-math-91068">\(27.199\)	\ (m=5\)” style="text-align:center;” class="lt-math-91068">\(28.627\)
\ (n\)” style="text-align:center;” class="lt-math-91068">8	\ (m=0\)” style="text-align:center;” class="lt-math-91068">\(24.352\)	\ (m=1\)” style="text-align:center;” class="lt-math-91068">\(25.904\)	\ (m=2\)” style="text-align:center;” class="lt-math-91068">\(27.421\)	\ (m=3\)” style="text-align:center;” class="lt-math-91068">\(28.908\)	\ (m=4\)” style="text-align:center;” class="lt-math-91068">\(30.371\)	\ (m=5\)” style="text-align:center;” class="lt-math-91068">\(31.812\)
\ (n\)” style="text-align:center;” class="lt-math-91068">9	\ (m=0\)” style="text-align:center;” class="lt-math-91068">\(27.493\)	\ (m=1\)” style="text-align:center;” class="lt-math-91068">\(29.047\)	\ (m=2\)” style="text-align:center;” class="lt-math-91068">\(30.569\)	\ (m=3\)” style="text-align:center;” class="lt-math-91068">\(32.065\)	\ (m=4\)” style="text-align:center;” class="lt-math-91068">\(33.537\)	\ (m=5\)” style="text-align:center;” class="lt-math-91068">\(34.989\)

Función generadora.

\[e^{x\left(t-\dfrac{1}{t}\right) / 2}=\sum_{n=-\infty}^{\infty} J_{n}(x) t^{n}, \quad x>0, t \neq 0 \nonumber \]

Representación Integral.

\[J_{n}(x)=\dfrac{1}{\pi} \int_{0}^{\pi} \cos (x \sin \theta-n \theta) d \theta, \quad x>0, n \in Z \nonumber \]