5.3: Solución de ODEs usando Transformadas de Laplace
- Page ID
- 119718
UNA DE LAS APLICACIONES TÍPICAS DE LAS TRANSFORMAS DE LAPLACE es la solución de ecuaciones diferenciales lineales no homogéneas En los siguientes ejemplos vamos a mostrar cómo funciona esto.
La idea general es que se transforma la ecuación para una función desconocida\(y(t)\) en una ecuación algebraica para su transformación,\(Y(t)\). Por lo general, la ecuación algebraica es fácil de\(Y(s)\) resolver en función de\(s\). Luego, uno se transforma de nuevo en\(t\) -espacio usando tablas de transformación de Laplace y las propiedades de Laplace transforma. El esquema se muestra en la Figura\(5 \cdot 2 .\)
Resolver el problema de valor inicial\(y^{\prime}+3 y=e^{2 t}, y(0)=1\).
El primer paso es realizar una transformación de Laplace del problema de valor inicial. La transformación del lado izquierdo de la ecuación es
\[\mathcal{L}\left[y^{\prime}+3 y\right]=s Y-y(0)+3 Y=(s+3) Y-1 \nonumber \]
Transformando el lado derecho, tenemos
\[\mathcal{L}\left[e^{2 t}\right]=\dfrac{1}{s-2} \nonumber \]
Combinando estos dos resultados, obtenemos
\[(s+3) Y-1=\dfrac{1}{s-2}\nonumber \]
El siguiente paso es resolver para\(Y(s)\):
\[Y(s)=\dfrac{1}{s+3}+\dfrac{1}{(s-2)(s+3)}\nonumber \]
Ahora necesitamos encontrar la transformada inversa de Laplace. Es decir, necesitamos averiguar qué función tiene una transformación de Laplace de la forma anterior. Utilizaremos las tablas de Laplace transform pairs. Posteriormente mostraremos que existen otros métodos para llevar a cabo la inversión de la transformación de Laplace.
La transformación inversa del primer término es\(e^{-3 t}\). Sin embargo, no hemos visto nada que se parezca a la segunda forma en la tabla de transformaciones que hemos compilado, pero podemos reescribir el segundo término usando una descomposición parcial de fracciones. Recordemos cómo hacer esto.
El objetivo es encontrar constantes\(A\) y\(B\) tales que
\[\dfrac{1}{(s-2)(s+3)}=\dfrac{A}{s-2}+\dfrac{B}{s+3} \nonumber \]
Elegimos esta forma porque sabemos que recombinar los dos términos en un término tendrá el mismo denominador. Solo tenemos que asegurarnos de que los numeradores estén de acuerdo después. Entonces, sumando los dos términos, tenemos
\[\dfrac{1}{(s-2)(s+3)}=\dfrac{A(s+3)+B(s-2)}{(s-2)(s+3)} \nonumber \]
Ecuación de numeradores,
\[1=A(s+3)+B(s-2)\nonumber \]
Hay varias formas de proceder en este punto.
a. Método 1.
Podemos reescribir la ecuación reuniendo términos con poderes comunes de\(s\), tenemos
\[(A+B) s+3 A-2 B=1 \nonumber \]
La única manera de que esto pueda ser cierto para todos\(s\) es que los coeficientes de las distintas potencias de\(s\) acuerdo en ambas partes. Esto lleva a dos ecuaciones para\(A\) y\(B\):
\[ \begin{array}{r} A+B=0 \\ 3 A-2 B=1 \end{array}\label{5.15} \]
La primera ecuación da\(A=-B\), por lo que la segunda ecuación se convierte\(-5 B=1 .\) La solución es entonces\(A=-B=\dfrac{1}{5} .\)
b. Método 2.
Dado que la ecuación\(\dfrac{1}{(s-2)(s+3)}=\dfrac{A}{s-2}+\dfrac{B}{s+3}\) es cierta para todos\(s\), podemos escoger valores específicos. Para\(s=2\), encontramos\(1=5 A\), o\(A=\dfrac{1}{5} .\) Para\(s=-3\), encontramos, o\(B=-\dfrac{1}{5} .\) Así\(1=-5 B\), obtenemos el mismo resultado que el Método 1, pero mucho más rápido.
Este es un ejemplo de llevar a cabo una descomposición parcial de la fracción.
c. Método 3.
Podríamos simplemente inspeccionar el problema original de la fracción parcial. Como el numerador no tiene\(s\) términos, podríamos adivinar la forma
\[\dfrac{1}{(s-2)(s+3)}=\dfrac{1}{s-2}-\dfrac{1}{s+3} \nonumber \]
Pero, recombinando los términos en el lado derecho, vemos que
\[\dfrac{1}{s-2}-\dfrac{1}{s+3}=\dfrac{5}{(s-2)(s+3)}\nonumber \]
Como estuvimos apagados por 5, dividimos las fracciones parciales por 5 para obtener
\[\dfrac{1}{(s-2)(s+3)}=\dfrac{1}{5}\left[\dfrac{1}{s-2}-\dfrac{1}{s+3}\right]\nonumber \]
que una vez más da la forma deseada.
Volviendo al problema, hemos encontrado que
\[Y(s)=\dfrac{1}{s+3}+\dfrac{1}{5}\left(\dfrac{1}{s-2}-\dfrac{1}{s+3}\right)\nonumber \]
Ahora podemos ver que la función con esta transformación de Laplace viene dada por
\(y(t)=\mathcal{L}^{-1}\left[\dfrac{1}{s+3}+\dfrac{1}{5}\left(\dfrac{1}{s-2}-\dfrac{1}{s+3}\right)\right]=e^{-3 t}+\dfrac{1}{5}\left(e^{2 t}-e^{-3 t}\right)\)
obras. Simplificando, tenemos la solución del problema de valor inicial
\[y(t)=\dfrac{1}{5} e^{2 t}+\dfrac{4}{5} e^{-3 t}\nonumber \]
Podemos verificar que hemos resuelto el problema de valor inicial.
\[y^{\prime}+3 y=\dfrac{2}{5} e^{2 t}-\dfrac{12}{5} e^{-3 t}+3\left(\dfrac{1}{5} e^{2 t}+\dfrac{4}{5} e^{-3 t}\right)=e^{2 t}\nonumber \]
y\(y(0)=\dfrac{1}{5}+\dfrac{4}{5}=1\).
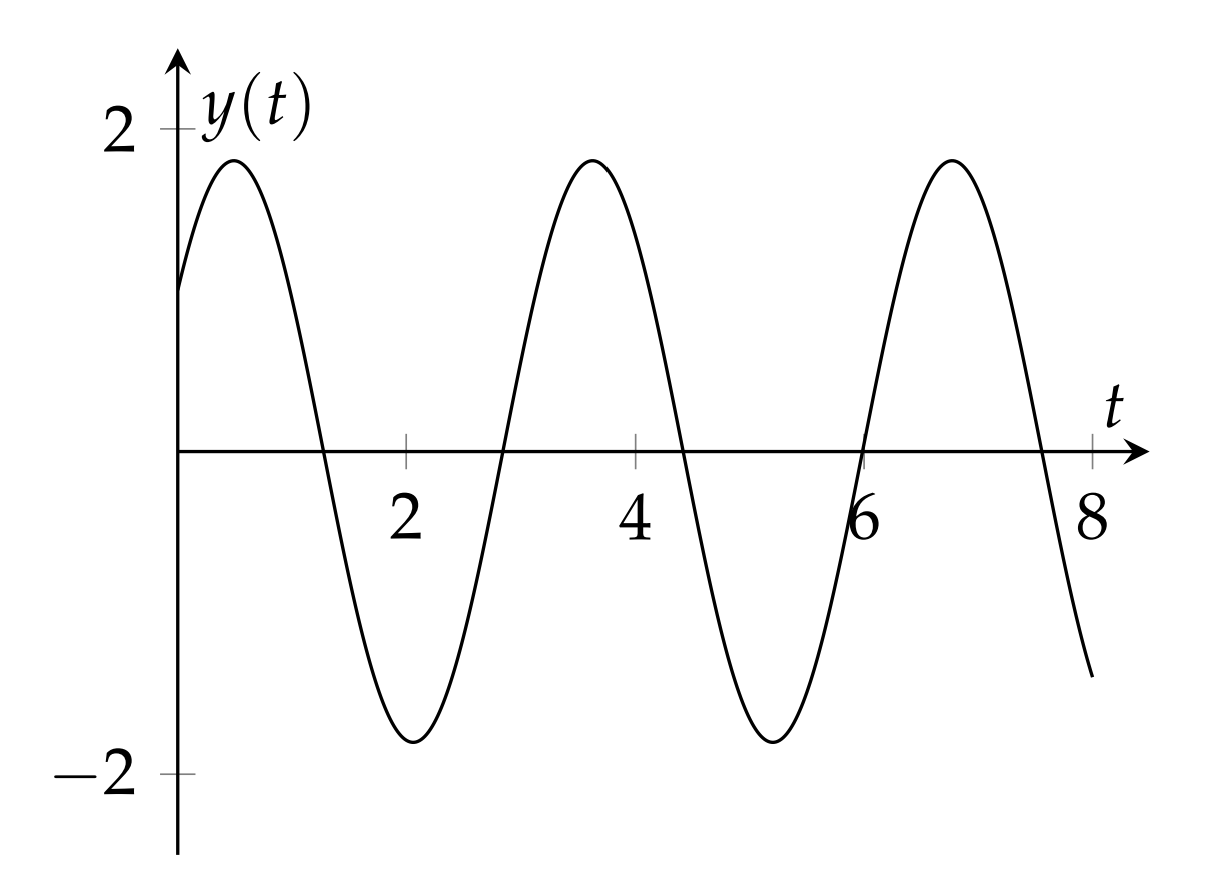
Resolver el problema de valor inicial\(y^{\prime \prime}+4 y=0, y(0)=1\),\(y^{\prime}(0)=3 .\)
Probablemente podamos resolver esto sin que Laplace se transforme, pero es un ejercicio sencillo. Transformando la ecuación, tenemos
\[\begin{aligned} 0 &=s^{2} Y-s y(0)-y^{\prime}(0)+4 Y \\ &=\left(s^{2}+4\right) Y-s-3 \end{aligned}\label{5.16} \]
Resolviendo para\(Y\), tenemos
\[Y(s)=\dfrac{s+3}{s^{2}+4}\nonumber \]
Ahora nos preguntamos si reconocemos el par de transformación necesario. El denominador parece el tipo necesario para la transformación de un seno o coseno. Sólo tenemos que jugar con el numerador. Dividiendo la expresión en dos términos, tenemos
\[Y(s)=\dfrac{s}{s^{2}+4}+\dfrac{3}{s^{2}+4}\nonumber \]
El primer término es ahora reconocible como la transformación de\(\cos 2 t\). El segundo término no es la transformación de\(\sin 2 t\). Sería si el numerador fuera un 2. Esto se puede corregir multiplicando y dividiendo por 2:
\[\dfrac{3}{s^{2}+4}=\dfrac{3}{2}\left(\dfrac{2}{s^{2}+4}\right)\nonumber \]
La solución se encuentra entonces como
\[y(t)=\mathcal{L}^{-1}\left[\dfrac{s}{s^{2}+4}+\dfrac{3}{2}\left(\dfrac{2}{s^{2}+4}\right)\right]=\cos 2 t+\dfrac{3}{2} \sin 2 t \nonumber \]
El lector puede verificar que esta es la solución del problema del valor inicial y se muestra en la Figura\(\PageIndex{2}\).