5.4: Funciones de Paso e Impulso
- Page ID
- 119740
Función de paso Heaviside
A MENUDOS, LOS PROBLEMAS DE VALOR INICIAL QUE SE ENFRENTE EN CURSOS DE ECUACIONES DIFERENCIALES SE PUEDEN RESOLVER UTILIZANDO EL MÉTODO Sin embargo, el uso de este último puede ser complicado e implica cierta habilidad con la integración. Muchos diseños de circuitos se pueden modelar con sistemas de ecuaciones diferenciales usando las Reglas de Kirchoff. Dichos sistemas pueden complicarse bastante. Sin embargo, las transformaciones de Laplace se pueden usar para resolver tales sistemas, y los ingenieros eléctricos han utilizado durante mucho tiempo dichos métodos en el análisis de circuitos.
En esta sección agregamos un par más de pares de transformación y propiedades de transformación que son útiles para dar cuenta de cosas como encender una fuerza impulsora, usar funciones periódicas como una onda cuadrada, o introducir fuerzas de impulso.
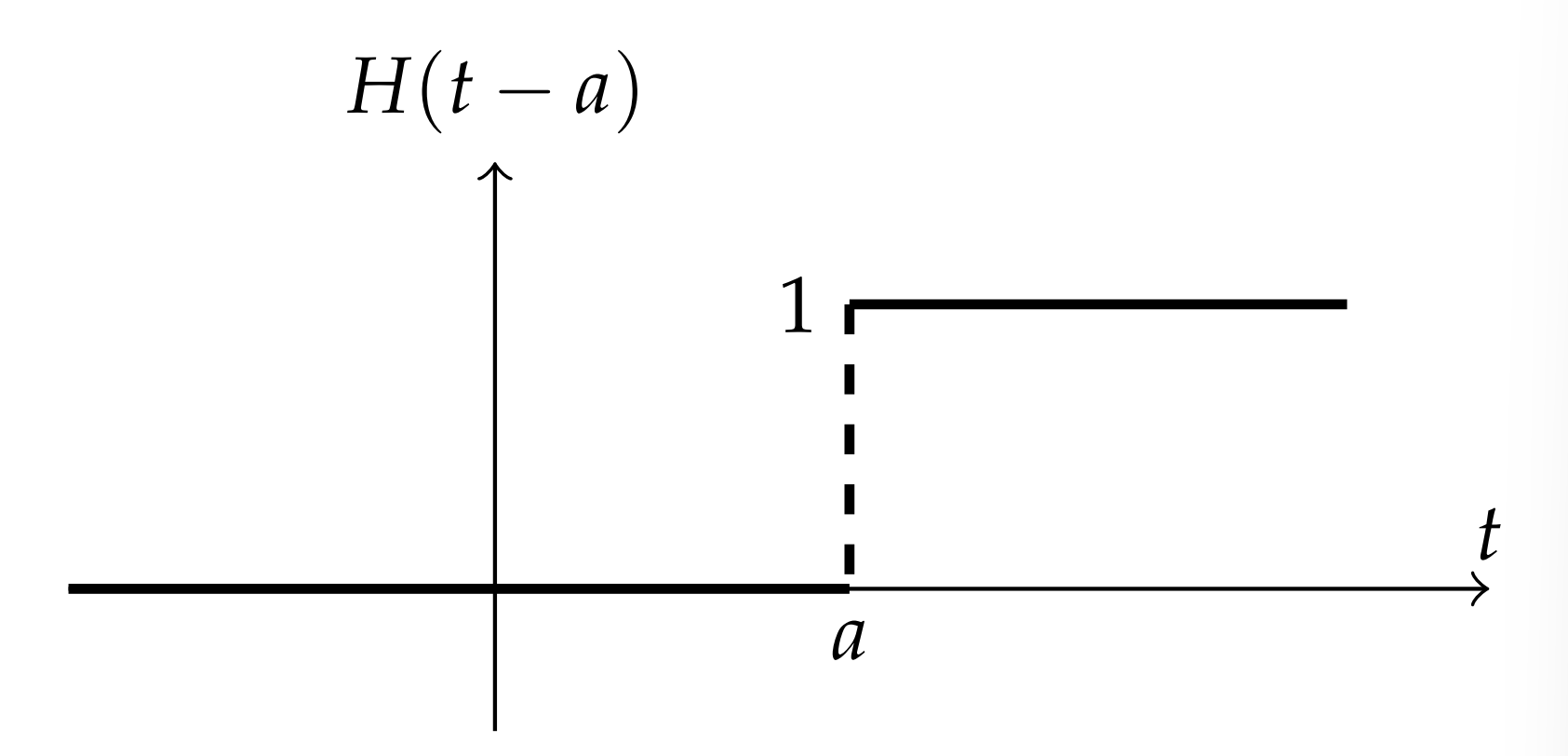
Primero recordamos la función de paso Heaviside, dada por
\[H(t)= \begin{cases}0, & t<0 \\ 1, & t>0\end{cases} \nonumber \]
. Una versión más general de la función de paso es la función de paso desplazada horizontalmente,\(H(t-a)\). Esta función se muestra en la Figura\(5 \cdot 5\). La transformación de Laplace de esta función se encuentra para\(a>0\) como
\ [\ begin {alineado}
\ mathcal {L} [H (t-a)] &=\ int_ {0} ^ {\ infty} H (t-a) e^ {-s t} d t\\
&=\ int_ {a} ^ {\ infty} e^ {-s t} d t\\
&=\ izquierda. \ dfrac {e^ {-s t}} {s}\ derecha|_ {a} ^ {\ infty} =\ dfrac {e^ {-a s}} {s}
\ final {alineado}\ etiqueta {5.18}\]
La transformación de Laplace tiene dos Teoremas de Cambio que implican la multiplicación de la función\(f(t)\), o su transformación\(F(s)\), por exponenciales. Los teoremas de las propiedades del primer y segundo turno son dados por
\[\mathcal{L}\left[e^{a t} f(t)\right]=F(s-a) \nonumber \]
\[\mathcal{L}[f(t-a) H(t-a)]=e^{-a s} F(s). \nonumber \]
(Los teoremas del Turno). Demostramos el Teorema del Primer Turno y dejamos la otra prueba como ejercicio para el lector. A saber,
\[ \begin{aligned} \mathcal{L}\left[e^{a t} f(t)\right] &=\int_{0}^{\infty} e^{a t} f(t) e^{-s t} d t \\ &=\int_{0}^{\infty} f(t) e^{-(s-a) t} d t=F(s-a) \end{aligned} \label{5.21} \]
Calcular la transformación de Laplace de\(e^{-a t} \sin \omega t\).
Esta función surge como la solución del oscilador armónico subamortiguado. Primero observamos que lo exponencial multiplica una función sinusoidal. El Teorema del Primer Turno nos dice que primero necesitamos la transformación de la función sinusoidal. Entonces, para\(f(t)=\sin \omega t\), tenemos
\[F(s)=\dfrac{\omega}{s^{2}+\omega^{2}}\nonumber \]
Usando esta transformación, podemos obtener la solución a este problema como
\[\mathcal{L}\left[e^{-a t} \sin \omega t\right]=F(s+a)=\dfrac{\omega}{(s+a)^{2}+\omega^{2}}\nonumber \]
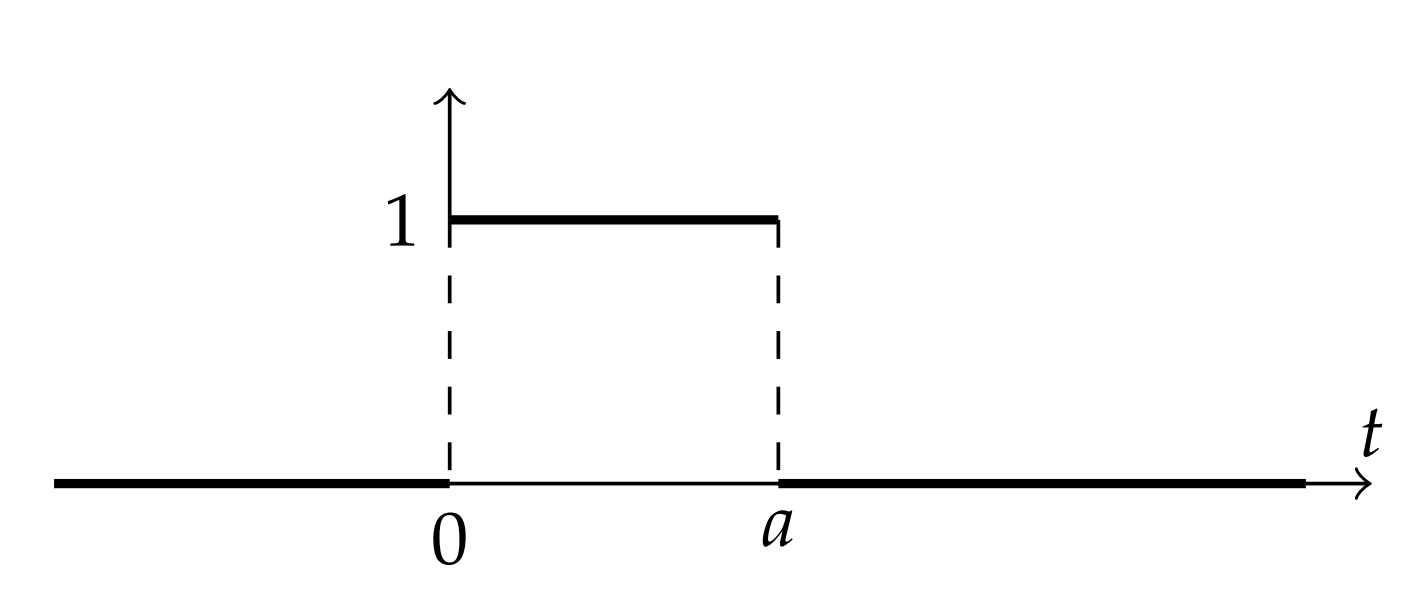
Se pueden encontrar ejemplos más interesantes usando funciones definidas por partes. Primero consideramos la función\(H(t)-H(t-a) .\) For\(t<0\), ambos términos son cero. En el intervalo\([0, a]\), la función\(H(t)=1\) y\(H(t-a)=0 .\) Por lo tanto,\(H(t)-H(t-a)=1\) para\(t \in[0, a]\). Por último, para\(t>a\), ambas funciones son una y por lo tanto la diferencia es cero. La gráfica de\(H(t)-H(t-a)\) se muestra en la Figura\(\PageIndex{2}.\)
Ahora consideramos la función definida por partes:
\ [g (t) =\ left\ {\ begin {array} {cc}
f (t), & 0\ leq t\ leq a\\
0, & ta<0, t>\
end {array}\ right. \ nonumber\]
Esta función se puede reescribir en términos de funciones de paso. Solo necesitamos multiplicar\(f(t)\) por la función de cuadro anterior,
\[g(t) = f(t)[H(t) − H(t − a)].\nonumber \]
Se representa esto en la Figura\(\PageIndex{3}.\)
Se pueden escribir funciones aún más complicadas en términos de funciones escalonadas. Solo necesitamos mirar sumas de funciones del formulario\(f(t)[H(t-a)-H(t-b)]\) para\(b>a\). Esto es similar a una función de caja. Es distinto de cero entre\(a\) y\(b\) y tiene altura\(f(t)\). Mostramos como ejemplo la función de onda cuadrada en la Figura\(\PageIndex{4}\). Se puede representar como una suma de un número infinito de cajas,
\[f(t)=\sum_{n=-\infty}^{\infty}[H(t-2 n a)-H(t-(2 n+1) a)]\nonumber \]
para\(a>0\)
Encuentra la Transformación de Laplace de una onda cuadrada “girada\(\mathrm{on}^{\prime \prime}\) en\(t=0 .\)
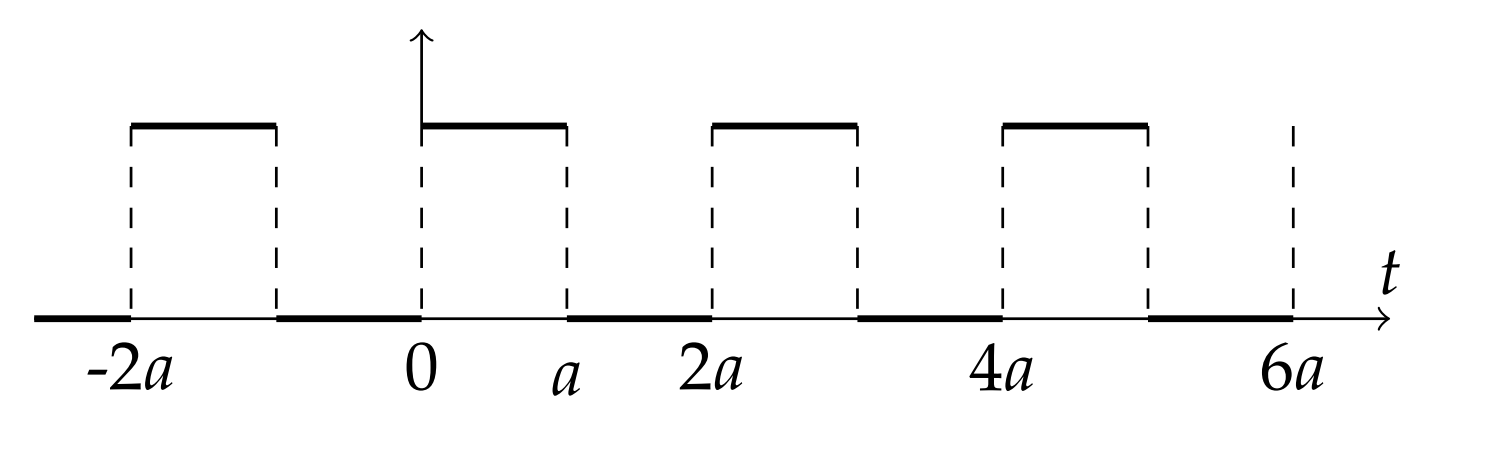
Dejamos
\[f(t)=\sum_{n=0}^{\infty}[H(t-2 n a)-H(t-(2 n+1) a)], \quad a>0 \nonumber \]
Usando las propiedades de la función Heaviside, tenemos
\[ \begin{aligned} \mathcal{L}[f(t)] &=\sum_{n=0}^{\infty}[\mathcal{L}[H(t-2 n a)]-\mathcal{L}[H(t-(2n+1)a)]]\\ &=\sum_{n=0}^{\infty}\left[\dfrac{e^{-2 n a s}}{s}-\dfrac{e^{-(2 n+1) a s}}{s}\right] \\ &=\dfrac{1-e^{-a s}}{s} \sum_{n=0}^{\infty}\left(e^{-2 a s}\right)^{n} \\ &=\dfrac{1-e^{-a s}}{s}\left(\dfrac{1}{1-e^{-2 a s}}\right) \\ &=\dfrac{1-e^{-a s}}{s\left(1-e^{-2 a s}\right)} \\ &=\dfrac{1}{s\left(1+e^{-a s}\right)} \end{aligned}\label{5.22} \]
Obsérvese que la tercera línea en la derivación es una serie geométrica. Resumimos esta serie para obtener la respuesta en una forma compacta desde\(e^{-2 a s}<\)\(1 .\)
Funciones Periódicas\(^{*}\)
El ejemplo anterior nos proporciona una función causal\((f(t)=0\) para la\(t<0 .)\) cual es periódica con periodo\(a\). Tales funciones periódicas pueden ser teadas de una manera más simple. Ahora vamos a demostrar que
(Transformación de Laplace de funciones periódicas).
Si\(f(t)\) es periódico con punto\(T\) y continuo por partes encendido\([0, T]\), entonces
\[F(s)=\dfrac{1}{1-e^{-s T}} \int_{0}^{T} f(t) e^{-s t} d t \nonumber \]
- Comprobante.
-
\[ \begin{aligned} F(s) &=\int_{0}^{\infty} f(t) e^{-s t} d t \\ &=\int_{0}^{T} f(t) e^{-s t} d t+\int_{T}^{\infty} f(t) e^{-s t} d t \\ &=\int_{0}^{T} f(t) e^{-s t} d t+\int_{T}^{\infty} f(t-T) e^{-s t} d t \\ &=\int_{0}^{T} f(t) e^{-s t} d t+e^{-s T} \int_{0}^{\infty} f(\tau) e^{-s \tau} d \tau \\ &=\int_{0}^{T} f(t) e^{-s t} d t+e^{-s T} F(s) \end{aligned} \label{5.23} \]
Resolviendo para\(F(s)\), se obtiene el resultado deseado.
Utilizar la periodicidad de
\[f(t)=\sum_{n=0}^{\infty}[H(t-2 n a)-H(t-(2 n+1) a) \nonumber], \quad a>0 \nonumber \]
para obtener la transformación de Laplace.
Observamos que\(f(t)\) tiene periodo\(T=2 a\). Por Teorema 5.1, tenemos
\[\begin{aligned} F(s) &=\int_{0}^{\infty} f(t) e^{-s t} d t \\ &=\dfrac{1}{1-e^{-2 a s}} \int_{0}^{2 a}[H(t)-H(t-a)] e^{-s t} d t \\ &=\dfrac{1}{1-e^{-2 a s}}\left[\int_{0}^{2 a} e^{-s t} d t-\int_{a}^{2 a} e^{-s t} d t\right] \\ &=\dfrac{1}{1-e^{-2 a s}}\left[\left.\dfrac{e^{-s t}}{-s}\right|_{0} ^{2 a}-\left.\dfrac{e^{-s t}}{-s}\right|_{a} ^{2 a}\right] \\ &=\dfrac{1}{s\left(1-e^{-2 a s}\right)}\left[1-e^{-2 a s}+e^{-2 a s}-e^{-a s}\right] \\ &=\dfrac{1-e^{-a s}}{s\left(1-e^{-2 a s}\right)} \\ &=\dfrac{1}{s\left(1+e^{-a s}\right)} \end{aligned}\label{5.24} \]
Este es el mismo resultado que se obtuvo en el ejemplo anterior.
P. A. M. Dirac\((1902-1984)\) introdujo la\(\delta\) función en su libro, Los principios de la mecánica cuántica, 4ª Ed.,\(\mathrm{Ox}-\) ford University Press, 1958, publicado originalmente en 1930, como parte de su declaración de ortogonalidad para una base de funciones en un espacio Hilbert ,\(\left\langle\xi^{\prime} \mid \xi^{\prime \prime}\right\rangle=\)\(c \delta\left(\xi^{\prime}-\zeta^{\prime \prime}\right)\) de la misma manera introdujimos la ortogonalidad discreta utilizando el delta de Kronecker. Históricamente, varios matemáticos buscaron comprender la función delta Diract, culminando en la teoría de las distribuciones de Laurent Schwartz (1915-2002) en 1945.
Función Dirac Delta
OTRO CONCEPTO ÚTIL ES LA FUNCIÓN DE IMPULSO. Si queremos aplicar una función de impulso, podemos usar la función delta de Dirac\(\delta(x)\). Este es un ejemplo de lo que se conoce como una función generalizada, o una distribución. Dirac había introducido esta función en los años 1930 en su estudio de la mecánica cuántica como herramienta útil. Posteriormente se estudió en una teoría general de las distribuciones y se encontró que era más que una simple herramienta utilizada por los físicos. La función delta de Dirac, como cualquier distribución, solo tiene sentido bajo una integral. Aquí se introducirá la función delta de Dirac a través de sus principales propiedades. La función delta satisface dos propiedades principales:
- \(\delta(x)=0\)para\(x \neq 0\).
- \(\int_{-\infty}^{\infty} \delta(x) d x=1\).
La integración en intervalos más generales da
\[ \int_{a}^{b} \delta(x) d x= \begin{cases}1, & 0 \in[a, b] \\ 0, & 0 \notin[a, b]\end{cases} \label{5.25} \]
Otra propiedad importante es la propiedad de tamizado:
\[\int_{-\infty}^{\infty} \delta(x-a) f(x) d x=f(a) \nonumber \]
Esto se puede ver al señalar que la función delta es cero en todas partes excepto en\(x=a\). Por lo tanto, el integrando es cero en todas partes y la única contribución de\(f(x)\) será de\(x=a\). Entonces, podemos sustituir por\(f(x)\)\(f(a)\) debajo de la integral. Ya que\(f(a)\) es una constante, tenemos que
\[ \begin{aligned} \int_{-\infty}^{\infty} \delta(x-a) f(x) d x &=\int_{-\infty}^{\infty} \delta(x-a) f(a) d x \\ &=f(a) \int_{-\infty}^{\infty} \delta(x-a) d x=f(a) \end{aligned} \label{5.26} \]
Evaluar:\(\int_{-\infty}^{\infty} \delta(x+3) x^{3} d x\)
Este es un uso simple de la propiedad de tamizado:
\[\int_{-\infty}^{\infty} \delta(x+3) x^{3} d x=(-3)^{3}=-27 \nonumber \]
Otra propiedad resulta del uso de un argumento escalado,\(ax\). En este caso, demostramos que
\[\delta(a x)=|a|^{-1} \delta(x) \nonumber \]
habitual, esto sólo tiene sentido bajo un signo integral. Entonces, colocamos\(\delta(a x)\) dentro de una integral y hacemos una sustitución\(y=a x\):
\[ \begin{aligned} \int_{-\infty}^{\infty} \delta(a x) d x &=\lim _{L \rightarrow \infty} \int_{-L}^{L} \delta(a x) d x \\ &=\lim _{L \rightarrow \infty} \dfrac{1}{a} \int_{-a L}^{a L} \delta(y) d y \end{aligned}\label{5.28} \]
Si\(a>0\) entonces
\[\int_{-\infty}^{\infty} \delta(a x) d x=\dfrac{1}{a} \int_{-\infty}^{\infty} \delta(y) d y \nonumber \]
Sin embargo, si\(a<0\) entonces
\[\int_{-\infty}^{\infty} \delta(a x) d x=\dfrac{1}{a} \int_{\infty}^{-\infty} \delta(y) d y=-\dfrac{1}{a} \int_{-\infty}^{\infty} \delta(y) d y \nonumber \]
La diferencia general en un signo menos multiplicativo puede ser absorbida en una expresión cambiando el factor\(1 / a\) a\(1 /|a| .\) Así,
\[\int_{-\infty}^{\infty} \delta(a x) d x=\dfrac{1}{|a|} \int_{-\infty}^{\infty} \delta(y) d y \nonumber \]
Propiedades de la función delta de Dirac:
\[\begin{aligned} & \begin{gathered}\int_{-\infty}^{\infty} \delta(x-a) f(x) d x=f(a) . \\\int_{-\infty}^{\infty} \delta(a x) d x=\dfrac{1}{|a|} \int_{-\infty}^{\infty} \delta(y) d y .\end{gathered} \end{aligned} \nonumber \]
Evaluar\(\int_{-\infty}^{\infty}(5 x+1) \delta(4(x-2)) d x\)
Esta es una integración sencilla:
\[\int_{-\infty}^{\infty}(5 x+1) \delta(4(x-2)) d x=\dfrac{1}{4} \int_{-\infty}^{\infty}(5 x+1) \delta(x-2) d x=\dfrac{11}{4} \nonumber \]
El primer paso es escribir\(\delta(4(x-2))=\dfrac{1}{4} \delta(x-2) .\) Entonces, la evaluación final viene dada por
\[\dfrac{1}{4} \int_{-\infty}^{\infty}(5 x+1) \delta(x-2) d x=\dfrac{1}{4}(5(2)+1)=\dfrac{11}{4} \nonumber \]
La función delta Dirac se puede utilizar para representar un impulso unitario. Sumando varios impulsos, o fuentes puntuales, podemos describir una función general como se muestra en la Figura 5.9. La suma de impulsos ubicados en puntos\(a_{i}\),\(i=1, \ldots, n\), con fortalezas\(f\left(a_{i}\right)\) estaría dada por
\[f(x)=\sum_{i=1}^{n} f\left(a_{i}\right) \delta\left(x-a_{i}\right)\nonumber \]
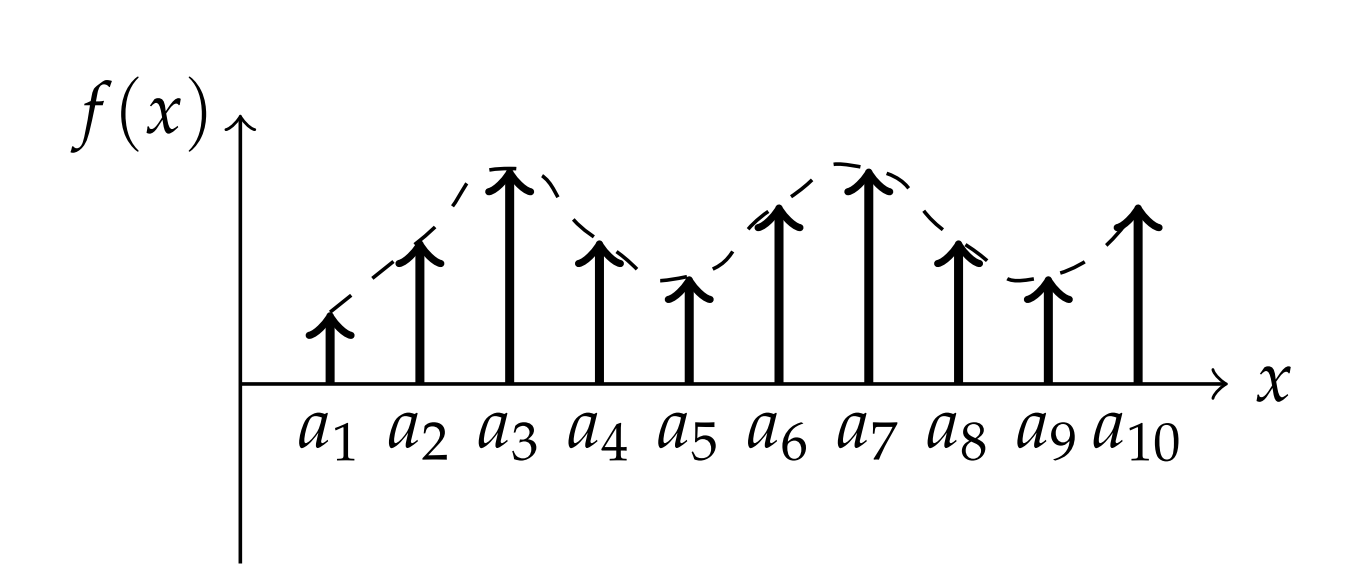
Una suma continua podría escribirse como
\[f(x)=\int_{-\infty}^{\infty} f(\xi) \delta(x-\xi) d \xi \nonumber \]
Esto es simplemente una aplicación de la propiedad de tamizado de la función delta.
Investigaremos un caso en el que se usaría un solo impulso. Mientras que una masa en un resorte está experimentando un simple movimiento armónico, la golpeamos por un instante a la vez\(t = a\). En tal caso, podríamos representar la fuerza como un múltiplo de\(\delta(t − a) \\).
Entonces se necesitaría la transformación Laplace de la función delta para resolver el problema de valor inicial asociado. Insertando la función delta en la transformada de Laplace, encontramos que para\(a>0\),
\[ \begin{aligned} \mathcal{L}[\delta(t-a)] &=\int_{0}^{\infty} \delta(t-a) e^{-s t} d t \\ &=\int_{-\infty}^{\infty} \delta(t-a) e^{-s t} d t \\ &=e^{-a s} \end{aligned} \label{5.30} \]
Resolver el problema de valor inicial\(y^{\prime \prime}+4 \pi^{2} y=\delta(t-2)\),
Este problema de valor inicial modela una oscilación de resorte con una fuerza de impulso. Sin el término forzoso, dado por la función delta, esta primavera está inicialmente en reposo y no estirada. La función delta modela un impulso unitario en\(t=2\). Por supuesto, anticipamos que en este momento la primavera comenzará a oscilar. Vamos a resolver este problema usando Laplace\(y(0)=y^{\prime}(0)=0\). transforma. Primero, transformamos la ecuación diferencial:
\[s^{2} Y-s y(0)-y^{\prime}(0)+4 \pi^{2} Y=e^{-2 s}\nonumber \]
Insertando las condiciones iniciales, tenemos
\[\left(s^{2}+4 \pi^{2}\right) Y=e^{-2 s}\nonumber \]
Resolviendo para\(Y(s)\), obtenemos
\[Y(s)=\dfrac{e^{-2 s}}{s^{2}+4 \pi^{2}}\nonumber \]
Buscamos ahora la función para la que esta es la transformación de Laplace. La forma de esta función es un exponencial veces que algunos Laplace transforman,\(F(s)\). Así, necesitamos el Teorema del Segundo Turno ya que la solución es de la forma\(Y(s)=e^{-2 s} F(s)\) para
\[F(s)=\dfrac{1}{s^{2}+4 \pi^{2}}.\nonumber \]
Necesitamos encontrar el correspondiente del par\(f(t)\) de transformaciones de Laplace. El denominador en\(F(s)\) sugiere un seno o coseno. Como el numerador es constante, elegimos seno. De las mesas de transformaciones, tenemos
\[\mathcal{L}[\sin 2 \pi t]=\dfrac{2 \pi}{s^{2}+4 \pi^{2}}\nonumber \]
Entonces, escribimos
\[F(s)=\dfrac{1}{2 \pi} \dfrac{2 \pi}{s^{2}+4 \pi^{2}}\nonumber \]
Esto da\(f(t)=(2 \pi)^{-1} \sin 2 \pi t\).
Ahora aplicamos el Teorema del Segundo Turno\(\mathcal{L}[f(t-a) H(t-a)]=\)\(e^{-a s} F(s)\), o
\[ \begin{aligned} y(t) &=\mathcal{L}^{-1}\left[e^{-2 s} F(s)\right] \\ &=H(t-2) f(t-2) \\ &=\dfrac{1}{2 \pi} H(t-2) \sin 2 \pi(t-2) \end{aligned}\label{5.31} \]
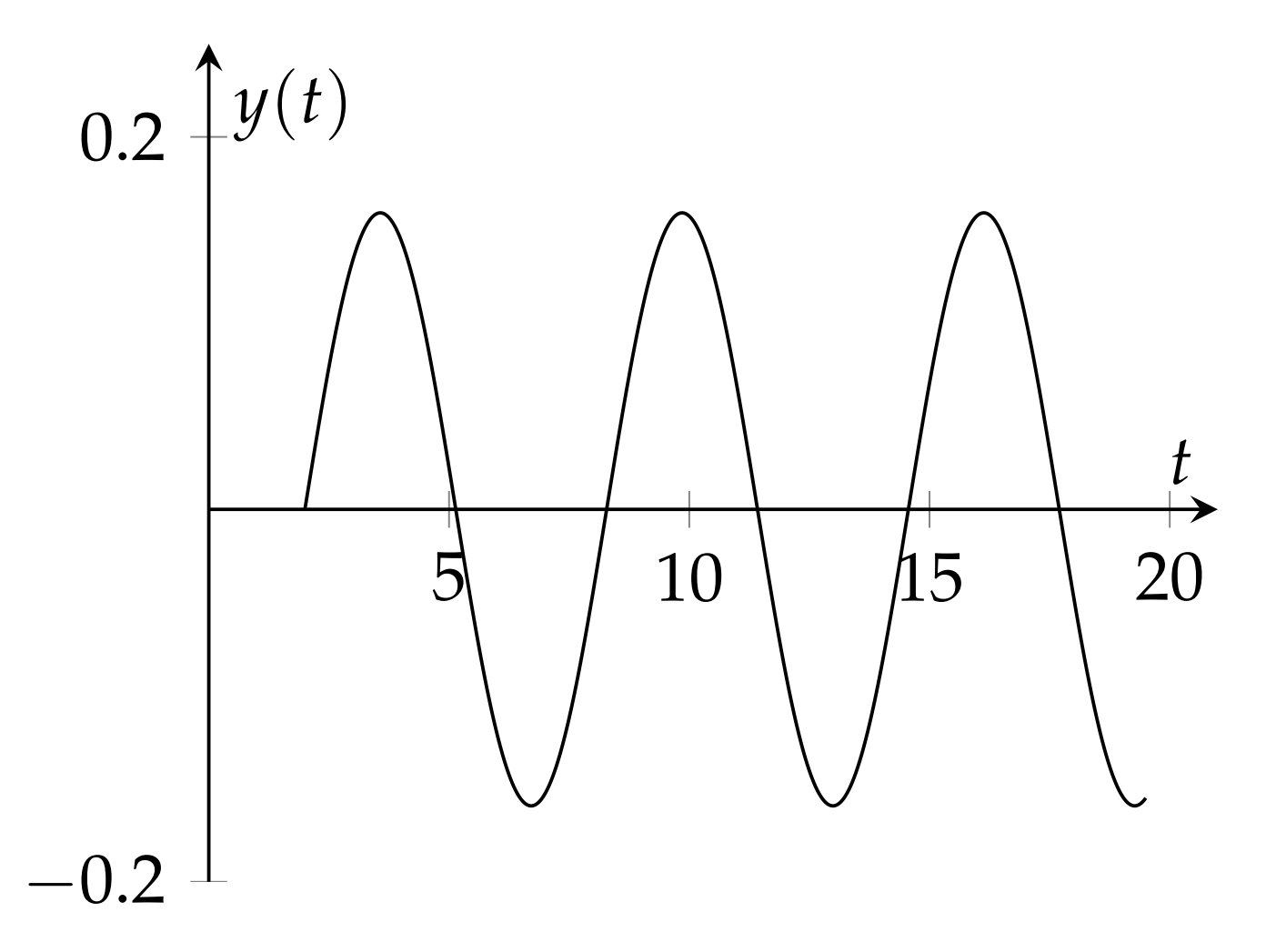
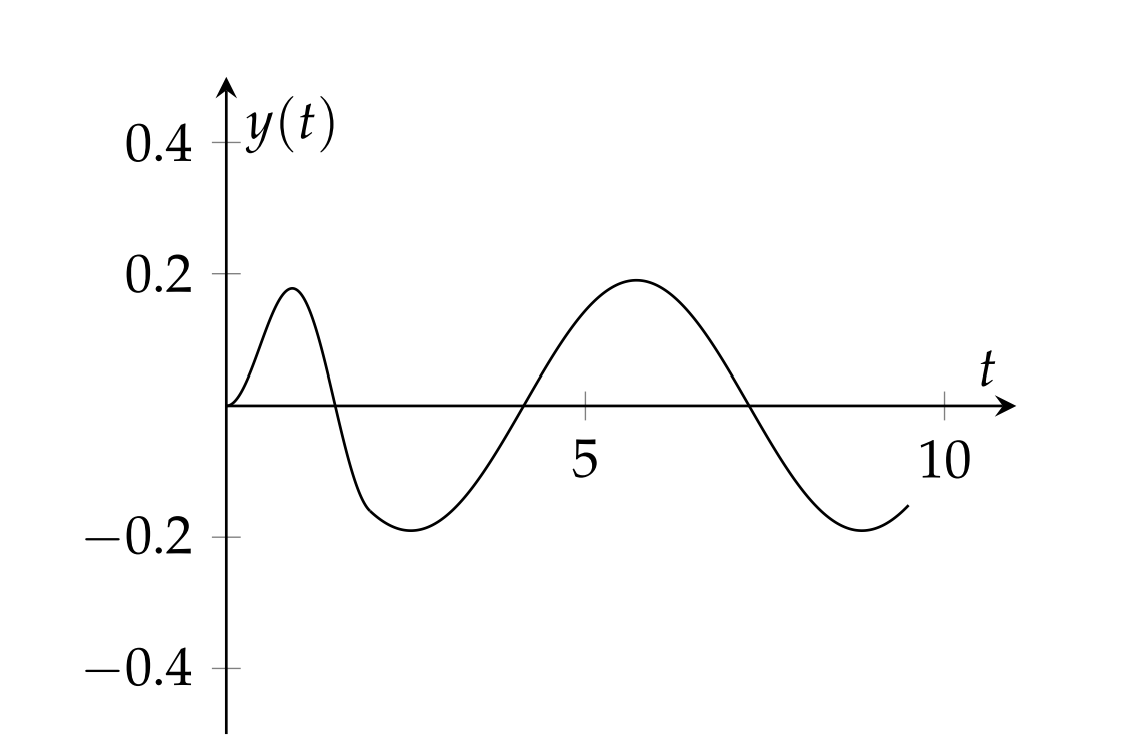
Esta solución nos dice que la masa está en reposo hasta\(t=2\) y después amplia\(5.14\) en la que un resorte en reposo excomienza a oscilar a su frecuencia natural. Una gráfica de esta solución es periencias una fuerza de impulso a\(t=2\). mostrado en la Figura\(\PageIndex{6}\)
Resolver el problema de valor inicial
\[y^{\prime \prime}+y=f(t), \quad y(0)=0, y^{\prime}(0)=0 \nonumber \]
donde
\[f(t)=\left\{\begin{array}{cl} \cos \pi t, & 0 \leq t \leq 2 \\ 0, & \text { otherwise } \end{array}\right. \nonumber \]
Necesitamos la transformación de Laplace de f (t). Esta función se puede escribir en términos de una función Heaviside,\(f(t) = cos \pi tH(t − 2)\). Para aplicar el Teorema del Segundo Turno, necesitamos una versión desplazada de la función coseno. Encontramos la versión desplazada al señalar que\(\cos \pi(t-2)=\cos \pi t\). Por lo tanto, tenemos
\[ \begin{aligned} f(t) &=\cos \pi t[H(t)-H(t-2)] \\ &=\cos \pi t-\cos \pi(t-2) H(t-2), \quad t \geq 0 \end{aligned} \label{5.32} \]
La transformación de Laplace de este término impulsor es
\[F(s)=\left(1-e^{-2 s}\right) \mathcal{L}[\cos \pi t]=\left(1-e^{-2 s}\right) \dfrac{s}{s^{2}+\pi^{2}} \nonumber \]
Ahora podemos proceder a resolver el problema de valor inicial. La transformación de Laplace del problema de valor inicial rinde
\[\left(s^{2}+1\right) Y(s)=\left(1-e^{-2 s}\right) \dfrac{s}{s^{2}+\pi^{2}}\nonumber \]
Por lo tanto,
\[Y(s)=\left(1-e^{-2 s}\right) \dfrac{s}{\left(s^{2}+\pi^{2}\right)\left(s^{2}+1\right)}\nonumber \]
Podemos recuperar la solución al problema del valor inicial usando el Teorema del Segundo Turno. La solución es de la forma\(Y(s)=(1-\)\(\left.e^{-2 s}\right) G(s)\) para
\[G(s)=\dfrac{s}{\left(s^{2}+\pi^{2}\right)\left(s^{2}+1\right)}\nonumber \]
Entonces, la solución final toma la forma
\[y(t)=g(t)-g(t-2) H(t-2)\nonumber \]
Sólo nos falta encontrar\(g(t)\) para poder acabar con el problema. Esto se hace fácilmente usando la descomposición parcial de la fracción
\[G(s)=\dfrac{s}{\left(s^{2}+\pi^{2}\right)\left(s^{2}+1\right)}=\dfrac{1}{\pi^{2}-1}\left[\dfrac{s}{s^{2}+1}-\dfrac{s}{s^{2}+\pi^{2}}\right]\nonumber \]
Entonces,
\[g(t)=\mathcal{L}^{-1}\left[\frac{s}{\left(s^{2}+\pi^{2}\right)\left(s^{2}+1\right)}\right]=\frac{1}{\pi^{2}-1}(\cos t-\cos \pi t)\nonumber \]
La solución final es dada entonces por
\[y(t)=\dfrac{1}{\pi^{2}-1}[\cos t-\cos \pi t-H(t-2)(\cos (t-2)-\cos \pi t)]\nonumber \]
Una gráfica de esta solución se muestra en la Figura\(\PageIndex{7}\).