5.6: Sistemas de ODEs

LAPACE TRANSFORMAS TAMBIÉN SON ÚTILES para resolver sistemas Estudiaremos sistemas lineales de ecuación diferencial en el Capítulo 6. Por ahora, solo veremos ejemplos sencillos de la aplicación de las transformaciones de Laplace.

Un ejemplo de un sistema de dos ecuaciones diferenciales para dos funciones desconocidas,\(x(t)\) y\(y(t)\), viene dado por el par de ecuaciones diferenciales acopladas

\[ \begin{aligned}&x^{\prime}=3 x+4 y \\ &y^{\prime}=2 x+y \end{aligned} \label{5.39} \]

Ninguna ecuación puede resolverse por sí sola sin el conocimiento de la otra función desconocida. Es por ello que se les llama pareja. También necesitaremos valores iniciales para el sistema. Nosotros elegiremos\(x(0)=1\) y\(y(0)=0\).

Ahora bien, ¿qué pasaría si tomáramos la transformación de Laplace de cada ecuación? Podemos aplicar las reglas como antes. Dejar que Laplace se transforme de\(x(t)\)\(X(t)\) y\(y(t)\) sea y\(Y(t)\), respectivamente, tenemos

\[ \begin{aligned}s X-1 &=3 X+4 Y, \\ s Y &=2 X+Y . \end{aligned} \label{5.40} \]

Hemos obtenido un sistema de ecuaciones algebraicas para\(X\) y\(Y\). Usando métodos estándar, como el Método de Cramer, podemos resolver este sistema de dos ecuaciones y dos incógnitas. Primero, reescribimos las ecuaciones como

\[ \begin{aligned}(s-3) X-4 Y &=1 \\ -2 X+(s-1) Y &=0 \end{aligned} \label{5.41} \]

Usando la regla (determinante) de Cramer para resolver tales sistemas, tenemos

\[X=\dfrac{\left|\begin{array}{cc} 1 & -4 \\ 0 & s-1 \end{array}\right|}{\left|\begin{array}{cc} s-3 & -4 \\ -2 & s-1 \end{array}\right|}, \quad Y=\dfrac{\left|\begin{array}{cc} s-3 & 1 \\ -2 & 0 \end{array}\right|}{\left|\begin{array}{cc} s-3 & -4 \\ -2 & s-1 \end{array}\right|} \nonumber \]

Obsérvese que el denominador en cada solución es un\(2 \times 2\) determinante que consiste en los coeficientes de\(X\) y\(Y\) en el orden apropiado. Los numeradores son el mismo determinante pero con el lado derecho de la ecuación reemplazando las columnas respectivas.

Computación de los determinantes, utilizando

\[\left|\begin{array}{ll} a & b \\ c & d \end{array}\right|=a d-b c \nonumber \]

tenemos

\[X=\dfrac{1}{(s-3)(s-1)-8}, \quad Y=\dfrac{2}{(s-3)(s-1)-8} \nonumber \]

o

\[X=\dfrac{s-1}{s^{2}-4 s-5}, \quad Y=\dfrac{2}{s^{2}-4 s-5}\nonumber \]

Ahora conocemos las transformaciones de Laplace de las soluciones, por lo que una simple transformación inversa de Laplace está en orden. Los denominadores son los mismos,

\[s^{2}-4 s-5=(s-5)(s+1)\nonumber \]

Podemos aplicar una descomposición parcial de la fracción a cada función para obtener

\[\begin{aligned}X &=\dfrac{s-1}{(s-5)(s+1)} \\ &=\dfrac{s-5+4}{(s-5)(s+1)} \\ &=\dfrac{1}{s+1}+\dfrac{4}{(s-5)(s+1)} \\ &=\dfrac{1}{s+1}+\dfrac{2}{3}\left[\dfrac{1}{s-5}-\dfrac{1}{s+1}\right] \\ &=\dfrac{2}{3} \dfrac{1}{s-5}+\dfrac{1}{3} \dfrac{1}{s+1} \\ Y &=\dfrac{2}{(s-5)(s+1)} \\ &=\dfrac{1}{3}\left[\dfrac{1}{s-5}-\dfrac{1}{s+1}\right] \end{aligned} \nonumber \]

Entonces, las soluciones al sistema de ecuaciones diferenciales viene dada por

\[ \begin{aligned}&x(t)=\dfrac{2}{3} e^{5} t+\dfrac{1}{3} e^{-t} \\ &y(t)=\dfrac{1}{3}\left(e^{5 t}-e^{-t}\right) \end{aligned} \nonumber \]

Podemos verificar eso\(x(0)=1\) y\(y(0)=0\).

\[ \begin{aligned}x^{\prime} &=\dfrac{10}{3} e^{5 t}-\dfrac{1}{3} e^{-t} \\ 3 x+4 y &=\left(2 e^{5 t}+e^{-t}\right)+\dfrac{4}{3}\left(e^{5 t}-e^{-t}\right) \\ &=\dfrac{10}{3} e^{5 t}-\dfrac{1}{3} e^{-t} \\ y^{\prime} &=\dfrac{5}{3} e^{5 t}+\dfrac{1}{3} e^{-t} \\ 2 x+y &=\left(\dfrac{4}{3} e^{5 t}+\dfrac{2}{3} e^{-t}\right)+\dfrac{1}{3}\left(e^{5 t}-e^{-t}\right) \\ &=\dfrac{5}{3} e^{5 t}+\dfrac{1}{3} e^{-t} \end{aligned} \label{5.43} \]

Ejemplo\(\PageIndex{1}\)

Determine la corriente en la Figura\(\PageIndex{1}\) para los siguientes valores:\(i_1(0) = i_2(0) = i_3(0) = 0\) y

\[v(t)=\left\{\begin{array}{cl} v_{0}, & 0 \leq t \leq 3.0 \\ 0, & \text { otherwise } \end{array}\right. \nonumber \]

El problema puede ser modelado por un sistema de ecuaciones diferenciales. En la Figura\(\PageIndex{1}\) se indican tres corrientes. La Regla Point (Junction) de Kirchoff lo indica\(i_{1}=i_{2}+i_{3}\).

Figura\(\PageIndex{1}\): Un circuito con dos bucles que contiene dos resistencias y dos inductores en paralelo.

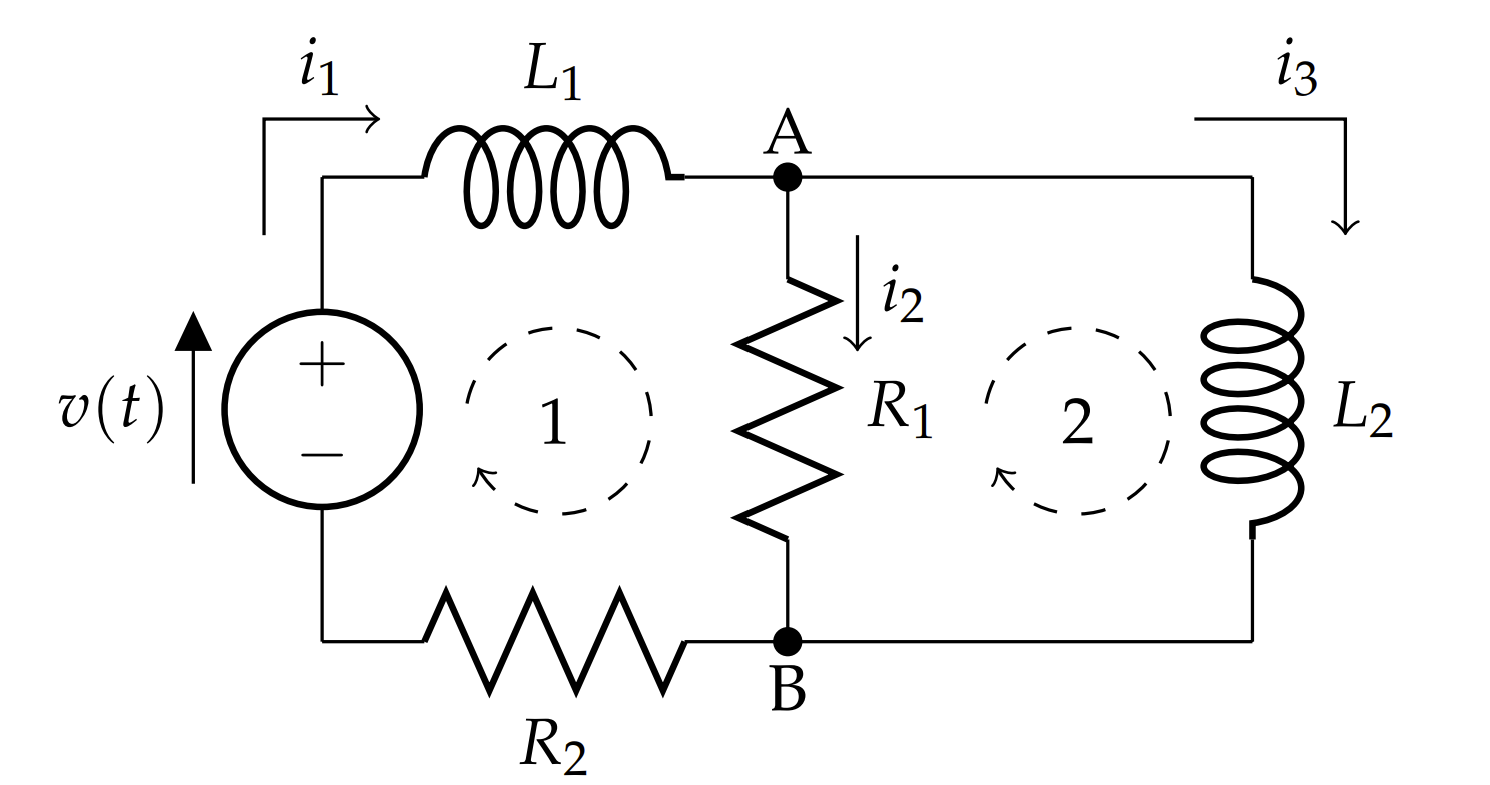
Para aplicar la Regla Loop de Kirchoff, necesitamos totalmente las caídas y subidas potenciales. Para las resistencias, estas provienen de la Ley de Ohm\(v=i R\),, y para los inductores, esta viene de la Ley de Faraday,\(v=L \dfrac{d i}{d t} .\) Para el bucle izquierdo (2), tenemos

\[L_{2} i_{3}^{\prime}=R_{1} i_{2} \nonumber \]

donde el primo denota la derivada del tiempo. Para el bucle correcto (1), tenemos

\[L_{1} i_{1}^{\prime}+R_{1} i_{2}+R_{2} i_{1}=v(t) \nonumber \]

Podemos usar la Regla de Puntos para eliminar una de las corrientes\(i_{2}=i_{1}-i_{3}\), dejando el modelo como dos ecuaciones diferenciales de primer orden,

\[ \begin{aligned}L_{2} i_{3}^{\prime}-R_{1}\left(i_{1}-i_{3}\right) &=0 \\ L_{1} i_{1}^{\prime}+R_{1}\left(i_{1}-i_{3}\right)+R_{2} i_{1} &=v(t) \end{aligned} \nonumber \]

O

\[ \begin{aligned}L_{2} i_{3}^{\prime}-R_{1} i_{1}+R_{1} i_{3} &=0 \\ L_{1} i_{1}^{\prime}+\left(R_{1}+R_{2}\right) i_{1}-R_{1} i_{3} &=v_{0}(1-H(t-3)) \end{aligned} \nonumber \]

donde\(H(t)\) está la función Heaviside.

Tomando la transformación de Laplace, asumiendo que\(i_{1}(0)=i_{2}(0)=0\), obtenemos el sistema algebraico de ecuaciones

\[ \begin{aligned}-R_{1} I_{1}+\left(s L_{2}+R_{1}\right) I_{3} &=0 \\ \left(s L_{1}+R_{1}+R_{2}\right) I_{1}-R_{1} I_{3} &=\dfrac{v_{0}}{s}\left(1-e^{-3 s}\right) \end{aligned} \nonumber \]

Aquí\(I_{1}(s)\) y\(I_{3}(s)\) están las transformaciones de Laplace de\(i_{1}(t)\) y\(i_{3}(t)\), respectivamente.

Como antes, utilizamos la Regla de Cramer para encontrar las soluciones.

\ [\ begin {aligned}
&I_ {1} =\ dfrac {\ izquierda|\ begin {array} {cc}
0 & s L_ {2} +R_ {1}\
\ dfrac {v_ {0}} {s}\ left (1-e^ {-3 s}\ right) & -R_ {1}
\ end {array}\ derecha|} {\ izquierda |\ begin {array} {cc}
-R_ {1} & s L_ {2} +R_ {1}\\
s L_ {1} +R_ {1 } +R_ {2} & -R_ {1}
\ end {array}\ derecha|}\\
&=\ dfrac {-v_ {0}\ izquierda (s L_ {2} +R_ {1}\ derecha)\ izquierda (1-e^ {-3 s}\ derecha)} {s\ izquierda [R_ {1} ^ {2} -\ izquierda (s L_ {2} +R_ {1}\ derecha)\ izquierda (s L_ {1} +R_ {1} +R_ {2}\ derecha)\ derecha]}\\
&=\ dfrac {v_ {0}\ izquierda (s L_ {2} +R_ {1}\ derecha)\ izquierda (1-e^ {-3 s}\ derecha)} {s \ izquierda [\ izquierda (L_ {1} L_ {2}\ derecha) s^ {2} +\ izquierda (R_ {1} L_ {1} +L_ {2}\ izquierda (R_ {1} +R_ {2}\ derecha)\ derecha) S+R_ {1} R_ {2}\ derecha]}. \\
&I_ {3} =\ dfrac {\ izquierda|\ begin {array} {cc}
-R_ {1} & 0\\
s L_ {1} +R_ {1} +R_ {2} &\ dfrac {v_ {0}} {s}\ izquierda (1-e^ {-3 s}\ derecha)
\ end {array}\ derecha| {} ft|\ begin {array} {cc}
-R_ {1} & s L_ {2} +R_ {1}\\
s L_ {1} +R_ {1} +R _ {2} & -R_ {1}
\ end {array}\ derecha|}\\
&=\ dfrac {v_ {0} R_ {1}\ izquierda (1-e^ {-3 s}\ derecha)} {s\ izquierda [R_ {1} ^ {2} -\ izquierda (s L_ {2} +R_ {1}\ derecha)\ izquierda (s L_ {1}} +R_ {1} +R_ {2}\ derecha)\ derecha]}\\
&=\ dfrac {-v_ {0} R_ {1}\ izquierda (1-e^ {-3 s}\ derecha)} {s\ izquierda [\ izquierda (L_ {1} L_ {2}\ derecha) s^ {2} +\ izquierda (R_ {1} L_ {1} +L_ {2}\ izquierda (R_ {1} +R_ {2}\ derecha)\ derecha) S+R_ {1} R_ {2}\ derecha]}.
\ end {alineado}\ etiqueta {5.44}\]

El denominador en estas expresiones no puede ser factorizado. Entonces, para avanzar más, se necesitan valores específicos para las constantes. Vamos\(R_{1}=2.00 \Omega, R_{2}=18.0 \Omega, L_{1}=48.0 \mathrm{H}, L_{2}=6.00 \mathrm{H}\). y\(v_{0}=18\) V. Entonces,

\[ \begin{aligned}&I_{1}=\dfrac{3 s+1}{s(2 s+1)(4 s+1)}\left(1-e^{-3 s}\right) \\ &I_{3}=-\dfrac{1}{s(2 s+1)(4 s+1)}\left(1-e^{-3 s}\right) \end{aligned} \nonumber \]

Usando fracciones parciales en el coeficiente de\(\left(1-e^{-3 s}\right)\), encontramos que

\[ \begin{aligned}&\dfrac{3 s+1}{s(2 s+1)(4 s+1)}=\dfrac{1}{s}-\dfrac{2}{4 s+1}-\dfrac{1}{2 s+1} \\ &\dfrac{1}{s(2 s+1)(4 s+1)}=\dfrac{1}{s}-\dfrac{8}{4 s+1}+\dfrac{2}{2 s+1} \end{aligned} \nonumber \]

Esto da

\[ \begin{aligned}&I_{1}=\left(\dfrac{1}{s}-\dfrac{1}{2} \dfrac{1}{s+\dfrac{1}{4}}-\dfrac{1}{2} \dfrac{1}{s+\dfrac{1}{2}}\right)\left(1-e^{-3 s}\right) \\ &I_{3}=\left(-\dfrac{1}{s}+\dfrac{2}{s+\dfrac{1}{4}}-\dfrac{1}{s+\dfrac{1}{2}}\right)\left(1-e^{-3 s}\right) \end{aligned} \nonumber \]

Tomando la transformación inversa de Laplace, encontramos las soluciones

\[i_{1}=1-\dfrac{1}{2} e^{-\dfrac{t}{4}}-\dfrac{1}{2} e^{-\dfrac{t}{2}}+\left(-1+\dfrac{1}{2} e^{-\dfrac{t-3}{4}}+\dfrac{1}{2} e^{-\dfrac{t-3}{2}}\right) H(t-3) \nonumber \]

\ [=\ left\ {\ begin {array} {cc}
1-\ dfrac {1} {2} e^ {-\ dfrac {t} {4}} -\ dfrac {1} {2} e^ {-\ dfrac {t} {2}}, & t\ leq 3,\\
-\ dfrac {1} {2}\ left (1-eq ^ {\ dfrac {3} {4}}\ derecha) e^ {-\ dfrac {t} {4}} -\ dfrac {1} {2}\ izquierda (1-e^ {\ dfrac {3} {2}}\ derecha) e^ {-\ dfrac {t} {2}}, & t\ geq 3.
\ end {array}\ derecho. \ nonumber\]

Figura\(\PageIndex{2}\): Una gráfica de las corrientes vs tiempo para Ejemplo\(\PageIndex{1}\) con la tensión\(v(t)=v_{0}(1-H(t-3))\). La curva más alta representa\(i_{1}\) y la otra curva es\(-i_{3}\).

\ [\ begin {alineado}
i_ {3} &=-1+2 e^ {-\ dfrac {t} {4}} -e^ {-\ dfrac {t} {2}} +\ izquierda (1-2 e^ {-\ dfrac {t-3} {4}} +e^ {-\ dfrac {t-3} {2}}\ derecha) H (t-3). \\
&=\ izquierda\ {\ begin {array} {cc}
-1+2 e^ {-\ dfrac {t} {4}} -e^ {-\ dfrac {t} {2}}, & t\ leq 3\\
2\ izquierda (1-e^ {\ dfrac {3} {4}}\ derecha) e^ {-\ dfrac {t} {4}} -\ izquierda (1-e^ {\ dfrac {3} {2}}\ derecha) e^ {-\ dfrac {t} {2}}, & t\ geq 3
\ end {array}\ derecha.
\ end {alineado}\ nonumber\]

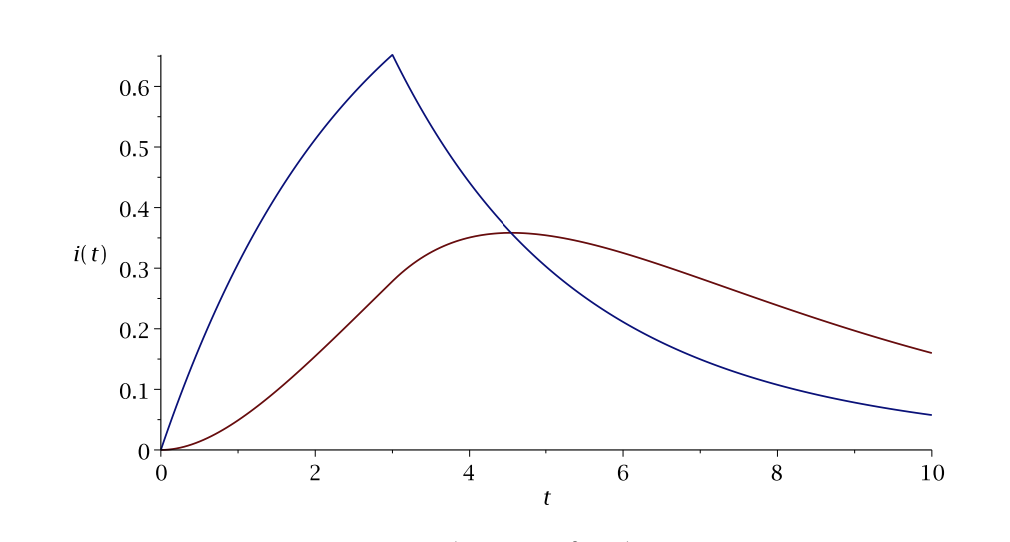
En la Figura\(\PageIndex{2}\), trazamos los currnts\(i_{1}\) y la otra curva\(-i\) es negativa, indicando un flujo a la inversa de la dirección en la Figura\(\PageIndex{1}\). No el cambio repentino\(i[1]\) en las\(t=3\), el momento en que se enciende el voltaje.

Se puede cambiar fácilmente el tiempo en que se aplica el voltaje. A saber, si

\ [v (t) =\ left\ {\ begin {array} {cc}
v_ {0}, & 0\ leq t\ leq t_ {0}\\
0, &\ text {de lo contrario}
\ end {array}\ derecha. \ nonumber\]

entonces las soluciones son dadas por

\[ \begin{aligned}&i_{1}=1-\dfrac{1}{2} e^{-\dfrac{t}{4}}-\dfrac{1}{2} e^{-\dfrac{t}{2}}+\left(-1+\dfrac{1}{2} e^{-\dfrac{t-t_{0}}{4}}+\dfrac{1}{2} e^{-\dfrac{t-t_{0}}{2}}\right) H\left(t-t_{0}\right) \\ &i_{3}=-1+2 e^{-\dfrac{t}{4}}-e^{-\dfrac{t}{2}}+\left(1-2 e^{-\dfrac{t-t_{0}}{4}}+e^{-\dfrac{t-t_{0}}{2}}\right) H\left(t-t_{0}\right) \end{aligned} \nonumber \]

Figura\(\PageIndex{3}\): Una gráfica de las corrientes vs tiempo para Ejemplo\(\PageIndex{1}\) para el voltaje dado por\(v(t)=v_{0}(1-H(t-10))\). La curva más alta representa\(i_{1}\) y la otra curva es\(-i_3\)

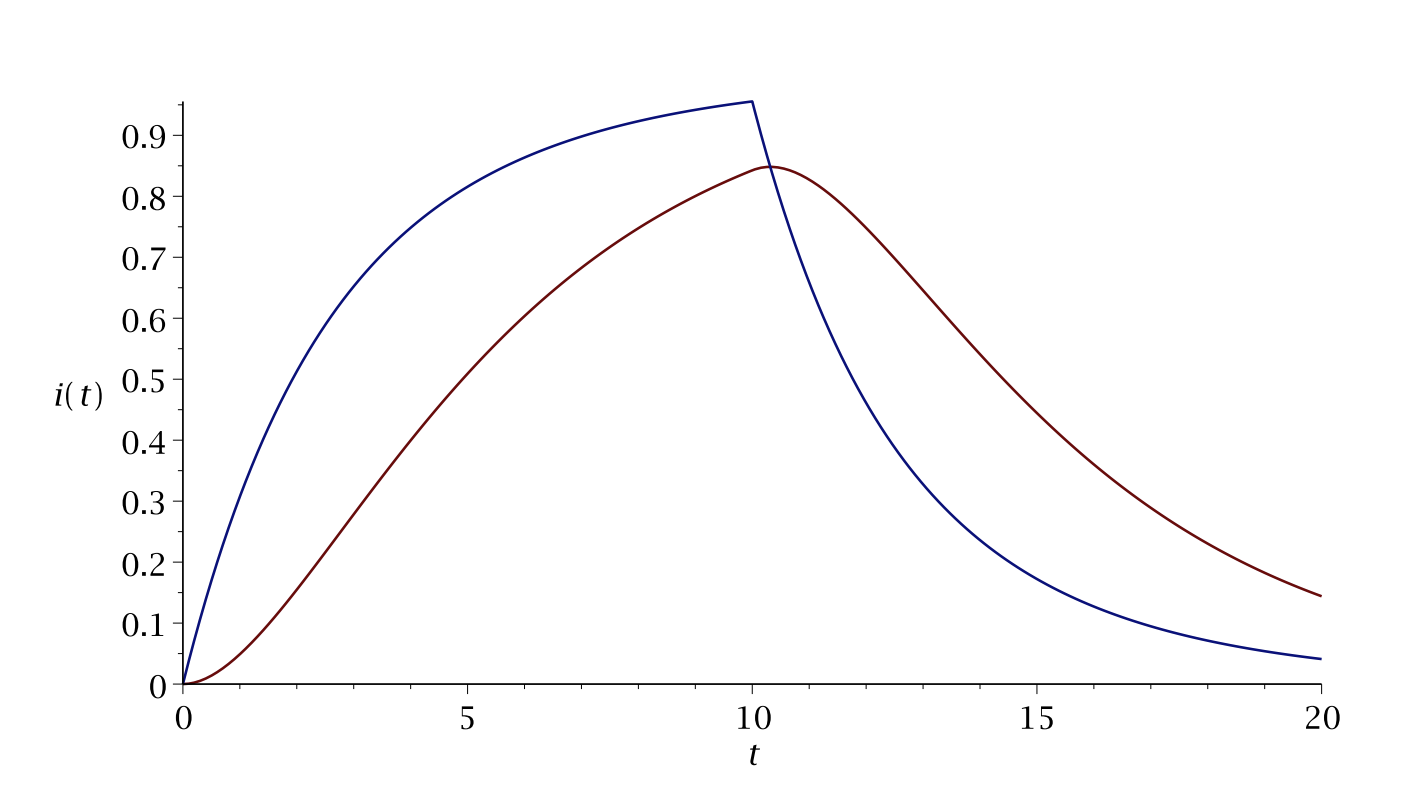
Una gráfica de las corrientes para\(t_{0}=10\) se muestran en la Figura\(\PageIndex{3}\).