6.9: Problemas

1. Considerar el sistema

\[\begin{gathered} x^{\prime}=-4 x-y \\ y^{\prime}=x-2 y \end{gathered} \nonumber \]

1. Determinar la ecuación diferencial de segundo orden satisfecha por\(x(t)\).
2. Resolver la ecuación diferencial para\(x(t)\).
3. Usando esta solución, encuentra\(y(t)\).
4. Verifique sus soluciones para\(x(t)\) y\(y(t)\).
5. Encontrar una solución particular al sistema dadas las condiciones iniciales\(x(0)=1\) y\(y(0)=0\).

2. Considera los siguientes sistemas. Determinar las familias de órbitas para cada sistema y esbozar varias órbitas en el plano de fase y clasificarlas por su tipo (nodo estable, etc.)
   1. \[\begin{aligned} &x^{\prime}=3 x \\ &y^{\prime}=-2 y . \end{aligned} \nonumber \]

   2. \[\begin{aligned} &x^{\prime}=-y \\ &y^{\prime}=-5 x \end{aligned} \nonumber \]

   3. \[\begin{aligned} &x^{\prime}=2 y \\ &y^{\prime}=-3 x \end{aligned} \nonumber \]

   4. \[\begin{aligned} &x^{\prime}=x-y \\ &y^{\prime}=y . \end{aligned} \nonumber \]

   5. \[\begin{aligned} x^{\prime} &=2 x+3 y \\ y^{\prime} &=-3 x+2 y \end{aligned} \nonumber \]

3. Utilizar las transformaciones que relacionan las coordenadas polares y cartesianas para demostrar que

\[\dfrac{d \theta}{d t}=\dfrac{1}{r^{2}}\left[x \dfrac{d y}{d t}-y \dfrac{d x}{d t}\right]\nonumber \]

4. Consideremos el sistema de ecuaciones en el Ejemplo 6.1.13.
   1. Derivar la forma polar del sistema.
   2. Resolver la ecuación radial\(r^{\prime}=r\left(1-r^{2}\right)\),, para los valores iniciales\(r(0)=0,0.5,1.0,2.0 .\)
   3. Con base en estas soluciones, graficar y describir el comportamiento de todas las soluciones al sistema original en coordenadas cartesianas.
5. Considera los siguientes sistemas. Para cada sistema determinar la matriz de coeficientes. Cuando sea posible, resolver el problema del valor propio para cada matriz y utilizar los valores propios y las funciones propias para proporcionar soluciones a los sistemas dados. Por último, en los casos comunes que investigaste en el Problema 2, haz comparaciones con tus respuestas anteriores, como qué tipo de valores propios corresponden a nodos estables.
   1. \[\begin{aligned} &x^{\prime}=3 x-y \\ &y^{\prime}=2 x-2 y \end{aligned} \nonumber \]

   2. \[\begin{aligned} &x^{\prime}=-y \\ &y^{\prime}=-5 x \end{aligned} \nonumber \]

   3. \[\begin{aligned} x^{\prime} &=x-y \\ y^{\prime} &=y . \end{aligned} \nonumber \]

   4. \[\begin{aligned} &x^{\prime}=2 x+3 y \\ &y^{\prime}=-3 x+2 y . \end{aligned} \nonumber \]

   5. \[\begin{aligned} &x^{\prime}=-4 x-y \\ &y^{\prime}=x-2 y \end{aligned} \nonumber \]

   6. \[\begin{aligned} &x^{\prime}=x-y \\ &y^{\prime}=x+y \end{aligned} \nonumber \]

6. Para la matriz dada, evaluar\(e^{t A}\), utilizando la definición

\[e^{t A}=\sum_{n=0}^{\infty} \dfrac{t^{n}}{n !} A^{n}=I+t A+\dfrac{t^{2}}{2} A^{2}+\dfrac{t^{3}}{3 !} A^{3}+\ldots\nonumber \]

y simplificando.

1. \(A=\left(\begin{array}{ll}1 & 0 \\ 0 & 2\end{array}\right)\)
2. \(A=\left(\begin{array}{cc}1 & 0 \\ -2 & 2\end{array}\right)\).
3. \(A=\left(\begin{array}{cc}0 & -1 \\ 0 & 1\end{array}\right)\).
4. \(A=\left(\begin{array}{ll}0 & 1 \\ 1 & 0\end{array}\right)\)
5. \(A=\left(\begin{array}{cc}0 & -i \\ i & 0\end{array}\right)\).
6. \(A=\left(\begin{array}{lll}0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0\end{array}\right)\)

7. Encuentre la solución de matriz fundamental para el sistema\(\mathbf{x}^{\prime}=A \mathbf{x}\) donde\(A\) se da la matriz. Si se proporciona una condición inicial, encuentre la solución del problema del valor inicial utilizando la matriz principal.
   1. \(A=\left(\begin{array}{cc}1 & 0 \\ -2 & 2\end{array}\right)\)
   2. \(A=\left(\begin{array}{cc}12 & -15 \\ 4 & -4\end{array}\right), \mathbf{x}(0)=\left(\begin{array}{l}1 \\ 0\end{array}\right)\)
   3. \(A=\left(\begin{array}{rr}2 & -1 \\ 5 & -2\end{array}\right)\).
   4. \(A=\left(\begin{array}{cc}4 & -13 \\ 2 & -6\end{array}\right), \mathbf{x}(0)=\left(\begin{array}{l}2 \\ 0\end{array}\right)\)
   5. \(A=\left(\begin{array}{ll}4 & 2 \\ 3 & 3\end{array}\right)\)
   6. \(A=\left(\begin{array}{cc}3 & 5 \\ -1 & 1\end{array}\right)\)
   7. \(A=\left(\begin{array}{cc}8 & -5 \\ 16 & 8\end{array}\right), \mathbf{x}(0)=\left(\begin{array}{c}1 \\ -1\end{array}\right)\)
   8. \(A=\left(\begin{array}{ll}1 & -2 \\ 2 & -3\end{array}\right)\).
   9. \(A=\left(\begin{array}{lll}5 & 4 & 2 \\ 4 & 5 & 2 \\ 2 & 2 & 2\end{array}\right)\)
8. Resolver los siguientes problemas de valor inicial utilizando la Ecuación 6.8.6, la solución de un sistema no homogéneo utilizando la solución de matriz principal.
   1. \[\mathbf{x}^{\prime}=\left(\begin{array}{cc} 2 & -1 \\ 3 & -2 \end{array}\right) \mathbf{x}+\left(\begin{array}{c} e^{t} \\ t \end{array}\right), \mathbf{x}(0)=\left(\begin{array}{l} 1 \\ 2 \end{array}\right) \nonumber \]

   2. \[\mathbf{x}^{\prime}=\left(\begin{array}{cc} 5 & 3 \\ -6 & -4 \end{array}\right) \mathbf{x}+\left(\begin{array}{c} 1 \\ e^{t} \end{array}\right), \mathbf{x}(0)=\left(\begin{array}{l} 1 \\ 0 \end{array}\right) \nonumber \]

   3. \[\mathbf{x}^{\prime}=\left(\begin{array}{cc} 2 & -1 \\ 5 & -2 \end{array}\right) \mathbf{x}+\left(\begin{array}{c} \cos t \\ \sin t \end{array}\right), \mathbf{x}(0)=\left(\begin{array}{l} 0 \\ 1 \end{array}\right) \nonumber \]

9. Agregar un tercer resorte conectado a la masa dos en el sistema acoplado que se muestra en la Figura 6.1.2 a una pared en el extremo derecho. Supongamos que las masas son iguales y los resortes son los mismos.
   1. Modele este sistema con un conjunto de ecuaciones diferenciales de primer orden.
   2. Si las masas son todas\(2.0 \mathrm{~kg}\) y las constantes de resorte son todas\(10.0\)\(\mathrm{N} / \mathrm{m}\), entonces encuentre la solución general para el sistema.
   3. Mover la masa uno a la izquierda (de equilibrio)\(10.0 \mathrm{~cm}\) y la masa dos a la derecha\(5.0 \mathrm{~cm}\). Déjalos ir. encontrar la solución y trazarla en función del tiempo. ¿Dónde está cada masa a los\(5.0\) segundos?
   4. Modele este problema de valor inicial con un conjunto de dos ecuaciones diferenciales de segundo orden. Configure el sistema en el formulario\(M \ddot{\mathbf{x}}=-K \mathbf{x}\) y resuelva usando los valores en parte\(b\).
10. En el Ejemplo 6.1.14 investigamos un sistema masa-resorte de pareja como un par de ecuaciones diferenciales de segundo orden.
    1. En ese problema usamos\(\sqrt{\dfrac{3 \pm \sqrt{5}}{2}}=\dfrac{\sqrt{5} \pm 1}{2}\). Demostrar este resultado.
    2. Reescribir el sistema como un sistema de cuatro ecuaciones de primer orden.
    3. Encuentre los valores propios y las funciones propias para el sistema de ecuaciones en la parte b para llegar a la solución que se encuentra en el Ejemplo 6.1.14.
    4. Dejar\(k=5.00 \mathrm{~N} / \mathrm{m}\) y\(m=0.250 \mathrm{~kg}\). Supongamos que las masas están inicialmente en reposo y graficar las posiciones en función del tiempo si inicialmente i)\(x_{1}(0)=x_{2}(0)=10.0 \mathrm{~cm}\) e i)\(x_{1}(0)=-x_{2}(0)=10.0\)\(\mathrm{cm}\). Describir el movimiento resultante.
11. Considere el circuito en serie de la Figura\(2.4\) con\(L=1.00 \mathrm{H}, R=1.00 \times 10^{2}\)\(\Omega, C=1.00 \times 10^{-4} \mathrm{~F}\), y\(V_{0}=1.00 \times 10^{3} \mathrm{~V}\)
    1. Configurar el problema como un sistema de dos ecuaciones diferenciales de primer orden para la carga y la corriente.
    2. Supongamos que no hay carga presente y no fluye corriente en el\(t=0\) momento en que\(V_{0}\) se aplica. Encuentra la corriente y la carga en el condensador como funciones del tiempo.
    3. Trace sus soluciones y describa cómo se comporta el sistema a lo largo del tiempo.
12. Considere el circuito en serie en la Figura 6.2.2.1 con\(L=1.00 \mathrm{H}, R_{1}=R_{2}=\)\(1.00 \times 10^{2} \Omega, C=1.00 \times 10^{-4} \mathrm{~F}\), y\(V_{0}=1.00 \times 10^{3} \mathrm{~V}\).
    1. Establecer el problema como un sistema de ecuaciones diferenciales de primer orden para las cargas y las corrientes en cada bucle.
    2. Supongamos que no hay carga presente y no fluye corriente en el\(t=0\) momento en que\(V_{0}\) se aplica. Encuentra la corriente y la carga en el condensador como funciones del tiempo.
    3. Trace sus soluciones y describa cómo se comporta el sistema a lo largo del tiempo.
13. Inicialmente se llena un tanque de 100 galones con agua pura. A la vez se agrega\(t=0\) agua con media libra de sal por cada dos galones al recipiente a razón de 3 galones por minuto, y la mezcla bien agitada se drena del recipiente a la misma velocidad.
    1. Encuentra el número de libras de sal en el recipiente en función del tiempo.
    2. ¿Cuántos minutos tarda la concentración en llegar a 2 libras por galón?
    3. ¿A qué se aproxima la concentración en el contenedor para grandes valores de tiempo? ¿Esto concuerda con tu intuición?
14. Se hacen dos cuartos de salsa para una fiesta. La receta requiere cinco cucharaditas de jugo de lima por cuarto de galón, pero accidentalmente habías puesto cinco cucharadas por cuarto de galón. De todas formas decides alimentar a tus invitados con la salsa. Asumir que los invitados toman un cuarto de taza de salsa por minuto y que reemplace lo que se tomó con tomates picados y cebollas sin ningún jugo de lima. [\(=4\)tazas de 1 cuarto de galón y\(1 \mathrm{~Tb}=3 \mathrm{tsp} .]\)
    1. Anote la ecuación diferencial y la condición inicial para la cantidad de jugo de lima en función del tiempo en este problema de tipo mezcla.
    2. Resolver este problema de valor inicial.
    3. ¿Cuánto tiempo tardará en que la salsa vuelva a la concentración sugerida por la receta?
15. Considera la reacción química que conduce al sistema en las Ecuaciones 6.2.4.3. Que las constantes de tasa sean\(k_{1}=0.20 \mathrm{~ms}^{-1}, k_{2}=0.05 \mathrm{~ms}^{-1}\), y\(k_{3}=0.10 \mathrm{~ms}^{-1}\). ¿Qué dicen los valores propios de la matriz de coeficientes sobre el comportamiento del sistema? Encuentre la solución del sistema asumiendo\([A](0)=A_{0}=1.0\)\(\mu \mathrm{mol},[B](0)=0\), y\([C](0)=0 .\) Trazar las soluciones para\(50.0 \mathrm{~ms}\) y describa lo que está sucediendo\(t=0.0\) a lo largo de este tiempo.
16. Encuentra y clasifica cualquier punto de equilibrio en el problema de Romeo y Julieta para los siguientes casos. Resolver los sistemas y describir sus afectos en función del tiempo.
    1. \(a=0, b=2, c=-1, d=0, R(0)=1, J(0)=1\).
    2. \(a=0, b=2, c=1, d=0, R(0)=1, J(0)=1\).
    3. \(a=-1, b=2, c=-1, d=0, R(0)=1, J(0)=1\).

Figura\(\PageIndex{1}\): Figura para el Problema 17.

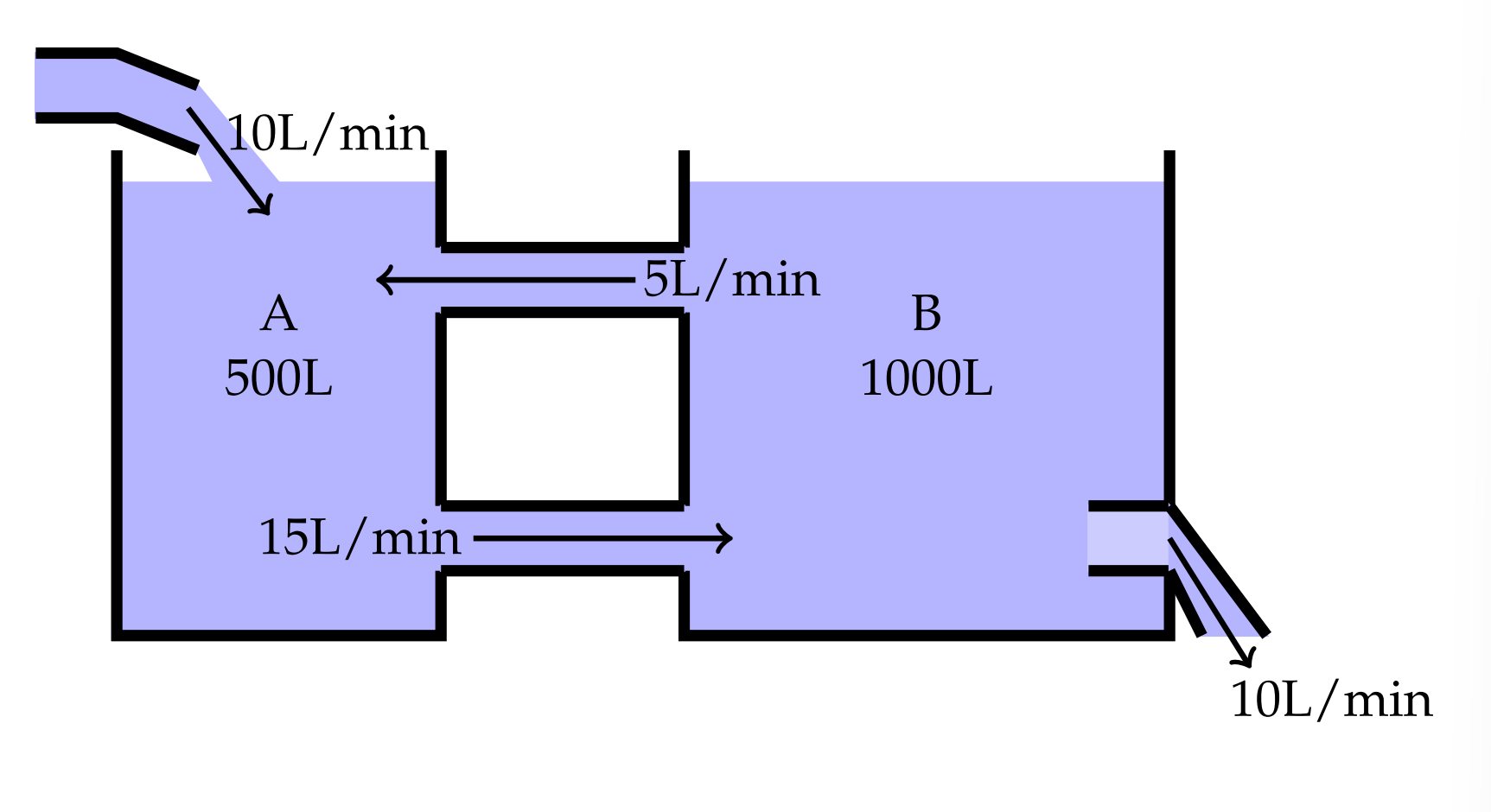
17. Dos tanques contienen una mezcla de agua y alcohol con tanque A que contiene\(500 \mathrm{~L}\) y tanque\(\mathrm{B}\) 1000 L. Inicialmente, la concentración de alcohol en Tanque\(\mathrm{A}\) es\(\mathrm{o} \%\) y la de\(\operatorname{tank} \mathrm{B}\) es\(8 \mathrm{o} \%\). La solución sale\(\operatorname{tank} \mathrm{A}\)\(\mathrm{B}\) a una velocidad de 15 litros/min y la solución en el tanque B vuelve a A a una velocidad de\(5 \mathrm{~L} / \mathrm{min}\) mientras que la solución bien mezclada también sale del sistema a 10 litros/min a través de una salida. Una mezcla de agua y alcohol entra\(\operatorname{tank} A\) a razón de 10 litros/min con la concentración de\(10 \%\) a través de una entrada. ¿Cuál será la concentración del alcohol de la solución en cada tanque después de 10 min?
18. Considera el sistema de tanques en el Problema 17. Agrega un tercio\(\operatorname{tank}(C)\) a\(\tan \mathrm{k} B\) con un volumen de\(300 \mathrm{~L}\). Conéctese\(C\) con\(8 \mathrm{~L} / \mathrm{min}\) desde\(\operatorname{tank} \mathrm{B}\) y\(2 \mathrm{~L} / \mathrm{min}\) fluya hacia atrás. Deja que io\(\mathrm{L} / \mathrm{min}\) fluya fuera del sistema. Si la concentración inicial está\(10 \%\) en cada tanque y una mezcla de agua y alcohol ingresa\(A\) al tanque a razón de 10 litros/min con la concentración de\(20 \%\) a través de una entrada, cuál será la concentración del alcohol en cada uno de los tanques después ¿una hora?
19. Consideremos el modelo epidémico que conduce al sistema en la Ecuación 6.2.7.1. Elija las constantes como\(a=2.0\) días\(^{-1}, d=3.0\) días\(^{-1}\) y\(r=1.0\) días\(^{-1}\). ¿Cuáles son los valores propios de la matriz de coeficientes? Encontrar la solución del sistema asumiendo una población inicial de 1,000 y un individuo infectado. Trazar las soluciones por\(5.0\) días y describir lo que está sucediendo\(t=0.0\) a lo largo de este tiempo. ¿Este modelo es realista?