8.1: Introducción

Última actualización
Guardar como PDF

Page ID: 119756

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

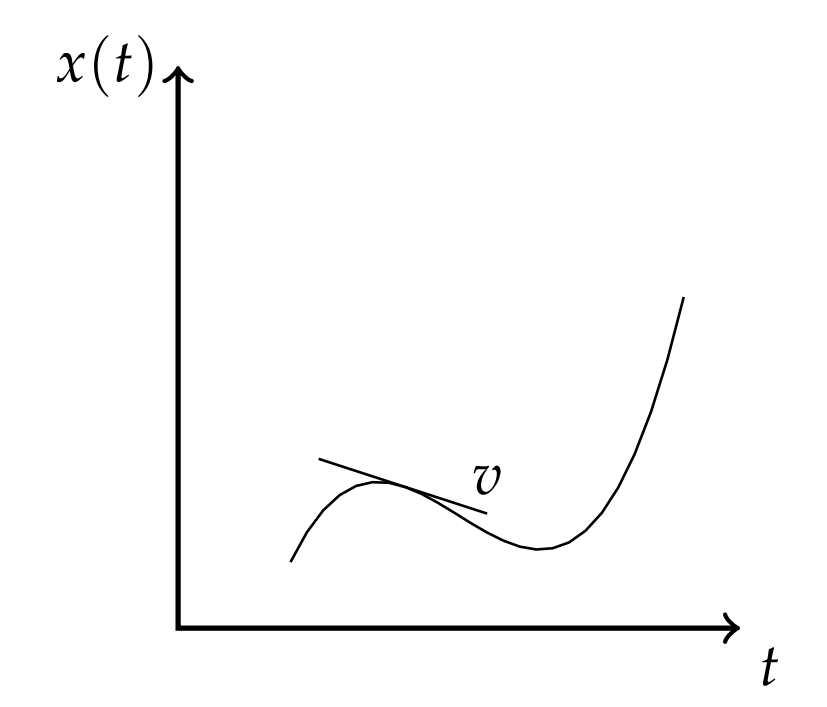
HAY DOS TEMAS PRINCIPALES EN EL CALCULO: derivados e integrales. Aprendió que los derivados son útiles para proporcionar tasas de cambio ya sea en el tiempo o en el espacio. Las integrales proporcionan áreas bajo curvas, pero también son útiles para proporcionar otros tipos de sumas sobre cuerpos continuos, como longitudes, áreas, volúmenes, momentos de inercia o integrales de flujo. En física, se pueden observar gráficas de posición versus tiempo y la pendiente (derivada) de tal función da la velocidad. (Ver Figura\(\PageIndex{1}\).) Al trazar velocidad versus tiempo puedes mirar la derivada para obtener aceleración, o podrías mirar el área bajo la curva y obtener el desplazamiento:

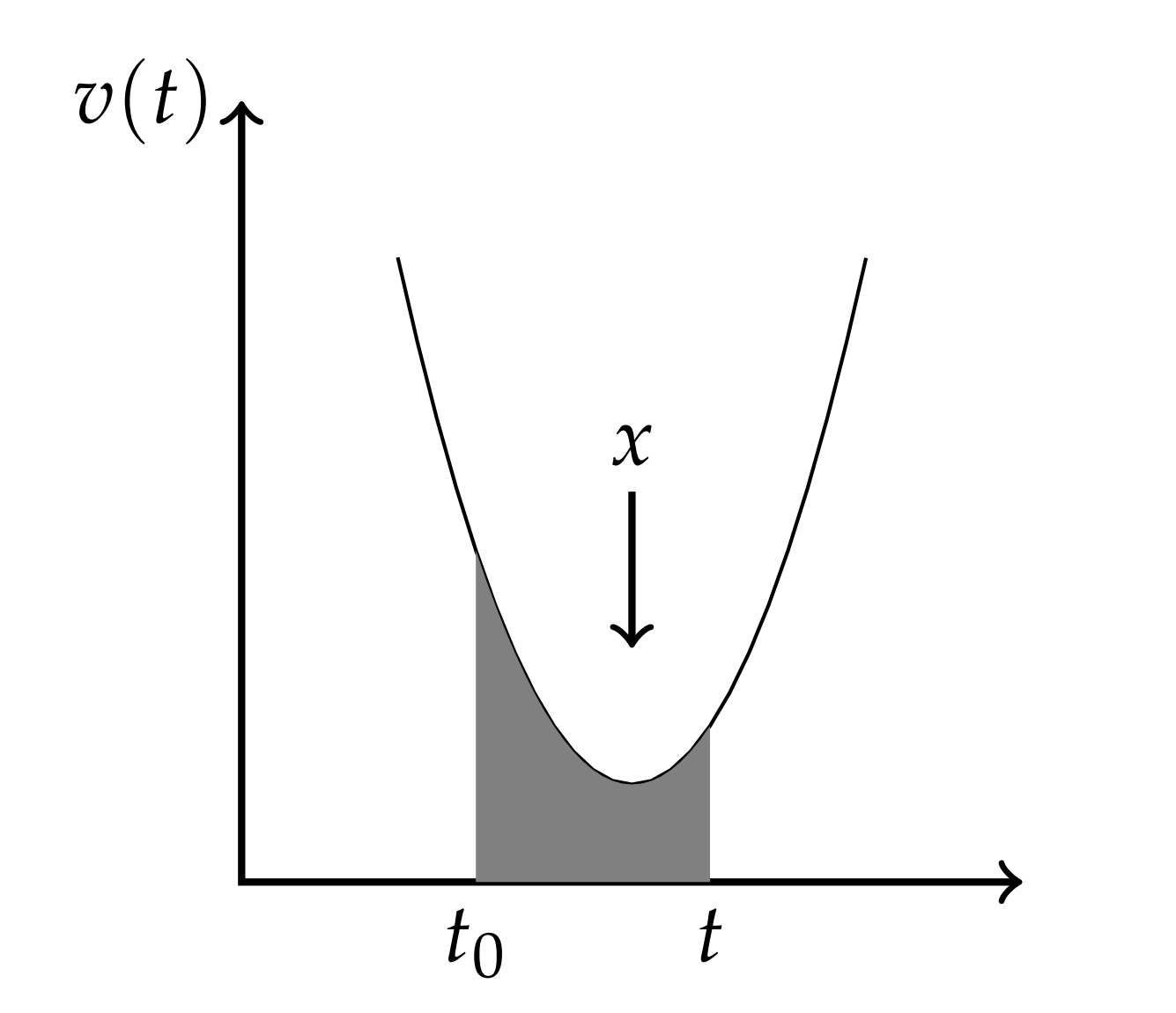
\[x=\int_{t_{0}}^{t} v d t \nonumber \]

Esto se muestra en la Figura\(\PageIndex{2}\).

Figura\(\PageIndex{1}\): Gráfica de posición vs tiempo.

Figura\(\PageIndex{2}\): Gráfica de velocidad vs tiempo.

Propiedades logarítmicas.

Por supuesto, necesitas saber diferenciar e integrar funciones dadas. Incluso antes de entrar en la diferenciación y la integración, es necesario tener una bolsa de funciones útiles en física. Las funciones comunes son las funciones polinómicas y racionales. Deberías estar bastante familiarizado con estos. Las funciones polinómicas toman la forma general

\[f(x)=a_{n} x^{n}+a_{n-1} x^{n-1}+\cdots+a_{1} x+a_{0} \nonumber \]

donde\(a_{n} \neq 0\). Esta es la forma de un polinomio de grado\(n\). Las funciones racionales\(f(x)=\dfrac{g(x)}{h(x)}\),, consisten en proporciones de polinomios. Sus gráficas pueden exhibir asíntotas verticales y horizontales.

A continuación se presentan las funciones exponenciales y logarítmicas. Los más comunes son el exponencial natural y el logaritmo natural. El exponencial natural viene dado por\(f(x)=e^{x}\), donde\(e \approx 2.718281828 \ldots\). El logaritmo natural es el inverso al exponencial, denotado por\(\ln x\). (Hay que tener cuidado, porque algunos libros de matemáticas y física utilizan log para significar exponencial natural, mientras que muchos de nosotros fuimos entrenados primero a\(\overline{\text { use }}\) esta notación para significar el logaritmo común, que es la 'base logarítmica 10'. Aquí vamos a utilizar\(\ln x\) para el logaritmo natural.)

(Propiedades Exponenciales). Las propiedades de la función exponencial se derivan de las propiedades básicas para los exponentes. A saber, tenemos:

\[e^{0} =1 \nonumber \]

\[e^{-a} =\dfrac{1}{e^{a}} \nonumber \]

\[e^{a} e^{b} =e^{a+b} \nonumber \]

\[ \left(e^{a}\right)^{b} =e^{a b} \nonumber \]

La relación entre el logaritmo natural y el exponencial natural viene dada por

\[y=e^{x} \Leftrightarrow x=\ln y \nonumber \]

(Propiedades logarítmicas). Algunas propiedades logarítmicas comunes son

\[\ln 1 =0 \nonumber \]

\[ \ln \dfrac{1}{a} =-\ln a \nonumber \]

\[ \ln (a b) =\ln a+\ln b \nonumber \]

\[ \ln \dfrac{a}{b} =\ln a-\ln b \nonumber \]

\[ \ln \dfrac{1}{b} =-\ln b \nonumber \]

Veremos aplicaciones de estas relaciones a medida que avancemos en el curso.