8.2: Funciones trigonométricas
- Page ID
- 119766
Otro conjunto de funciones útiles son las funciones trigonométricas. Estas funciones probablemente te han plagado desde la secundaria. Tienen sus orígenes ya en la construcción de las pirámides. Las aplicaciones típicas en tus clases introductorias de matemáticas probablemente hayan incluido encontrar las alturas de árboles, postes de bandera o edificios. Se reconoció hace mucho tiempo que triángulos rectos similares tienen relaciones fijas de cualquier par de lados de los dos triángulos similares. Estas relaciones solo cambian cuando cambian los ángulos no rectos.
Así, la relación de dos lados de un triángulo rectángulo solo depende del ángulo. Ya que hay seis posibles proporciones (¡piénsalo!) , entonces hay seis funciones posibles. Estos se designan como seno, coseno, tangente y sus recíprocos (cosecante, secante y cotangente). En tu clase introductoria de física, realmente solo necesitabas los tres primeros. También aprendiste que se representan como las proporciones de lo contrario a hipotenusa, adyacentes a hipotenusa, etc. ojalá ya tengas esto abajo.
También debes conocer los valores exactos de estas funciones trigonométricas básicas para los ángulos especiales\(\theta=0, \dfrac{\pi}{6}, \dfrac{\pi}{3}, \dfrac{\pi}{4}, \dfrac{\pi}{2}\), y sus ángulos correspondientes en el segundo, tercer y cuarto cuadrantes. Esto se interioriza después de mucho uso, pero proporcionamos estos valores en Table\(\PageIndex{1}\) solo en caso de que necesites un recordatorio.
| \(\theta\) | \(\cos \theta\) | \(\sin \theta\) | \(\tan \theta\) |
|---|---|---|---|
| \ (\ theta\)” style="text-align:center;” class="lt-math-91099">\(\mathrm{O}\) | \ (\ cos\ theta\)” style="text-align:center;” class="lt-math-91099">\(1\) | \ (\ sin\ theta\)” style="text-align:center;” class="lt-math-91099">\(\mathrm{O}\) | \ (\ tan\ theta\)” style="text-align:center;” class="lt-math-91099">\(\mathrm{O}\) |
| \ (\ theta\)” style="text-align:center;” class="lt-math-91099">\(\dfrac{\pi}{6}\) | \ (\ cos\ theta\)” style="text-align:center;” class="lt-math-91099">\(\dfrac{\sqrt{3}}{2}\) | \ (\ sin\ theta\)” style="text-align:center;” class="lt-math-91099">\(\dfrac{1}{2}\) | \ (\ tan\ theta\)” style="text-align:center;” class="lt-math-91099">\(\dfrac{\sqrt{3}}{3}\) |
| \ (\ theta\)” style="text-align:center;” class="lt-math-91099">\(\dfrac{\pi}{3}\) | \ (\ cos\ theta\)” style="text-align:center;” class="lt-math-91099">\(\dfrac{1}{2}\) | \ (\ sin\ theta\)” style="text-align:center;” class="lt-math-91099">\(\dfrac{\sqrt{3}}{2}\) | \ (\ tan\ theta\)” style="text-align:center;” class="lt-math-91099">\(\sqrt{3}\) |
| \ (\ theta\)” style="text-align:center;” class="lt-math-91099">\(\dfrac{\pi}{4}\) | \ (\ cos\ theta\)” style="text-align:center;” class="lt-math-91099">\(\dfrac{\sqrt{2}}{2}\) | \ (\ sin\ theta\)” style="text-align:center;” class="lt-math-91099">\(\dfrac{\sqrt{2}}{2}\) | \ (\ tan\ theta\)” style="text-align:center;” class="lt-math-91099">1 |
| \ (\ theta\)” style="text-align:center;” class="lt-math-91099">\(\dfrac{\pi}{2}\) | \ (\ cos\ theta\)” style="text-align:center;” class="lt-math-91099">\(\mathrm{0}\) | \ (\ sin\ theta\)” style="text-align:center;” class="lt-math-91099">1 | \ (\ tan\ theta\)” style="text-align:center;” class="lt-math-91099">undefined |
Los problemas que suelen tener los estudiantes al usar funciones trigonométricas en cursos posteriores provienen del uso o la recuperación de identidades. Tendremos muchas ocasiones para hacerlo en esta clase también. ¿Qué es una identidad? Es una relación que se mantiene cierta todo el tiempo. Por ejemplo, la identidad más común para las funciones trigonométricas es la identidad pitagórica
\[\sin ^{2} \theta+\cos ^{2} \theta=1 \nonumber \]
Esto es cierto para todos los ángulos\(\theta !\) Una identidad aún más simple es
\[\tan \theta=\dfrac{\sin \theta}{\cos \theta} \nonumber \]
Otras identidades simples pueden derivarse de la identidad pitagórica. Dividir la identidad por\(\cos ^{2} \theta\), o\(\sin ^{2} \theta\), rendimientos
\[\tan ^{2} \theta+1 =\sec ^{2} \theta \nonumber \]
\[1+\cot ^{2} \theta =\csc ^{2} \theta \nonumber \]
Varias otras identidades útiles provienen del uso del seno y el coseno de la suma y diferencia de dos ángulos. A saber, tenemos que
\[\sin (A \pm B)=\sin A \cos B \pm \sin B \cos A \nonumber \]
\[ \cos (A \pm B)=\cos A \cos B \mp \sin A \sin B \nonumber \]
Tenga en cuenta que los signos superiores (inferiores) se toman juntos.
Evaluar\(\sin \dfrac{\pi}{12}\).
Solución
\[ \begin{aligned} \sin \dfrac{\pi}{12} &=\sin \left(\dfrac{\pi}{3}-\dfrac{\pi}{4}\right) \\ &=\sin \dfrac{\pi}{3} \cos \dfrac{\pi}{4}-\sin \dfrac{\pi}{4} \cos \dfrac{\pi}{3} \\ &=\dfrac{\sqrt{3}}{2} \dfrac{\sqrt{2}}{2}-\dfrac{\sqrt{2}}{2} \dfrac{1}{2} \\ &=\dfrac{\sqrt{2}}{4}(\sqrt{3}-1) \end{aligned} \label{A.19} \]
(Fórmulas de ángulo doble). Las fórmulas de doble ángulo se encuentran configurando\(A=B:\)
\[\sin (2 A) =2 \sin A \cos B \nonumber \]
\[ \cos (2 A) =\cos ^{2} A-\sin ^{2} A \nonumber \]
Usando la ecuación\(\PageIndex{1}\), podemos reescribir la ecuación\(\PageIndex{9}\) como
\[\cos (2 A) =2 \cos ^{2} A-1 \nonumber \]
\[ =1-2 \sin ^{2} A \nonumber \]
(Fórmulas de medio ángulo). Estos, a su vez, conducen a las fórmulas de medio ángulo. Resolviendo para\(\cos ^{2} A\) y\(\sin ^{2} A\), encontramos que
\[\sin ^{2} A=\dfrac{1-\cos 2 A}{2} \nonumber \]
\[\cos ^{2} A=\dfrac{1+\cos 2 A}{2} \nonumber \]
Evaluar\(\cos \dfrac{\pi}{12}\).
Solución
En el último ejemplo, se utilizaron las identidades suma/diferencia para evaluar una expresión similar. También podríamos haber usado una identidad de medio ángulo. En este ejemplo, tenemos
\[ \begin{aligned} \cos ^{2} \dfrac{\pi}{12} &=\dfrac{1}{2}\left(1+\cos \dfrac{\pi}{6}\right) \\ &=\dfrac{1}{2}\left(1+\dfrac{\sqrt{3}}{2}\right) \\ &=\dfrac{1}{4}(2+\sqrt{3}) \end{aligned} \label{A.26} \]
Entonces,\(\cos \dfrac{\pi}{12}=\dfrac{1}{2} \sqrt{2+\sqrt{3}}\). Esta no es la forma más simple y se llama radical anidado. De hecho, si procediéramos a usar la identidad de diferencia para los cosenos, entonces obtendríamos
\[\cos \dfrac{\pi}{12}=\dfrac{\sqrt{2}}{4}(1+\sqrt{3}) \nonumber \]
Entonces, ¿cómo se demuestra que estas respuestas son las mismas?
Es útil a veces saber cuándo se pueden reducir las raíces cuadradas de tales radicales, llamadas denestores. De manera más general, se busca escribir\(\sqrt{a+b \sqrt{q}}=c+d \sqrt{q}\). Siguiendo el procedimiento de este ejemplo, se tiene\(d=\dfrac{b}{2 c}\) y
\[c^{2}=\dfrac{1}{2}\left(a \pm \sqrt{a^{2}-q b^{2}}\right) \text {. } \nonumber \]
Mientras\(a^{2}-q b^{2}\) sea un cuadrado perfecto, existe la posibilidad de reducir la expresión a una forma más simple.
Centrémonos en el factor\(\sqrt{2+\sqrt{3}}\). Buscamos escribir esto en la forma\(c+d \sqrt{3}\). Equiparando las dos expresiones y la cuadratura, tenemos
\[ \begin{aligned} 2+\sqrt{3} &=(c+d \sqrt{3})^{2} \\ &=c^{2}+3 d^{2}+2 c d \sqrt{3} \end{aligned} \label{A.27} \]
Con el fin de resolver por\(c\) y\(d\), parecería natural equiparar el
coeficientes de\(\sqrt{3}\) y los términos restantes. Obtenemos un sistema de dos ecuaciones algebraicas no lineales,
\[ c^{2}+3 d^{2} =2 \nonumber \]
\[2 c d =1 \nonumber \]
Resolviendo la segunda ecuación para\(d=1 / 2 c\), y sustituyendo el resultado en la primera ecuación, encontramos resultado en la primera ecuación, encontramos
\[4 c^{4}-8 c^{2}+3=0 \nonumber \]
Esta ecuación de cuarto orden tiene cuatro soluciones,
\[c=\pm \dfrac{\sqrt{2}}{2}, \pm \dfrac{\sqrt{6}}{2} \nonumber \]
y
\[b=\pm \dfrac{\sqrt{2}}{2}, \pm \dfrac{\sqrt{6}}{6} \nonumber \]
Por lo tanto,
\[ \begin{aligned} \cos \dfrac{\pi}{12} &=\dfrac{1}{2} \sqrt{2+\sqrt{3}} \\ &=\pm \dfrac{1}{2}\left(\dfrac{\sqrt{2}}{2}+\dfrac{\sqrt{2}}{2} \sqrt{3}\right) \\ &=\pm \dfrac{\sqrt{2}}{4}(1+\sqrt{3}) \end{aligned} \label{A.30} \]
y
\[ \begin{aligned} \cos \dfrac{\pi}{12} &=\dfrac{1}{2} \sqrt{2+\sqrt{3}} \\ &=\pm \dfrac{1}{2}\left(\dfrac{\sqrt{6}}{2}+\dfrac{\sqrt{6}}{6} \sqrt{3}\right) \\ &=\pm \dfrac{\sqrt{6}}{12}(3+\sqrt{3}) . \end{aligned} \label{A.31} \]
De las cuatro soluciones, dos son negativas y sabemos que el valor del coseno para este ángulo tiene que ser positivo. ¡Las dos soluciones restantes son realmente iguales! Un cálculo rápido verificará esto:
\[ \begin{aligned} \dfrac{\sqrt{6}}{12}(3+\sqrt{3}) &=\dfrac{\sqrt{3} \sqrt{2}}{12}(3+\sqrt{3}) \\ &=\dfrac{\sqrt{2}}{12}(3 \sqrt{3}+3) \\ &=\dfrac{\sqrt{2}}{4}(\sqrt{3}+1) \end{aligned} \label{A.32} \]
Podríamos haber pasado por alto esta situación requiriendo que las soluciones para\(b\) y no\(c\) fueran simplemente proporcionales a\(\sqrt{3}\) como son en el segundo caso.
Identidades de producto
Por último, otro conjunto útil de identidades son las identidades del producto. Por ejemplo, si agregamos las identidades para\(\sin (A+B)\) y\(\sin (A-B)\), los segundos términos cancelan y tenemos
\[\sin (A+B)+\sin (A-B)=2 \sin A \cos B \nonumber \]
Así, tenemos que
\[\sin A \cos B=\dfrac{1}{2}(\sin (A+B)+\sin (A-B)) \nonumber \]
Del mismo modo, tenemos
\[\cos A \cos B=\dfrac{1}{2}(\cos (A+B)+\cos (A-B)) \nonumber \]
y
\[\sin A \sin B=\dfrac{1}{2}(\cos (A-B)-\cos (A+B)) \nonumber \]
(¡Conoce las identidades en caja anteriores!) Estas ecuaciones en caja son las identidades trigonométricas más comunes. Aparecen a menudo y solo deberían rodar fuera de tu lengua.
También necesitaremos comprender los comportamientos de las funciones trigonométricas. En particular, sabemos que las funciones seno y coseno son periódicas. No son las únicas funciones periódicas, como veremos. [Simplemente visualice los dientes en una sierra de carpintero.] Sin embargo, son las funciones periódicas más comunes.
Una función periódica\(f(x)\) satisface la relación
\[f(x+p)=f(x), \quad \text { for all } x \nonumber \]
para alguna constante\(p\). Si\(p\) es el menor tal número, entonces\(p\) se llama el período. Tanto la función senoidal como la coseno tienen periodo\(2 \pi\). Esto significa que la gráfica repite su forma cada\(2 \pi\) unidad. De igual manera,\(\sin b x\) y\(\cos b x\) tienen el periodo común\(p=\dfrac{2 \pi}{b}\). Haremos uso de este hecho en capítulos posteriores.
En Feynman's ¡Seguramente estás bromeando señor Feynman! , Richard Feynman (1918-1988) habla sobre su invención de su propia notación tanto para funciones trigonométricas como trigonométricas inversas ya que la notación estándar no tenía sentido para él.
Relacionadas con estas son las funciones trigonométricas inversas. Por ejemplo,\(f(x)=\sin ^{-1} x\), o funciones\(f(x)=\arcsin x .\) inversas devuelven ángulos, así que deberías pensar
\[\theta=\sin ^{-1} x \quad \Leftrightarrow \quad x=\sin \theta \nonumber \]
Además, debe recordar que\(y=\sin ^{-1} x=\arcsin x\) es solo una función si existen relaciones\(-\dfrac{\pi}{2} \leq\)\(x \leq \dfrac{\pi}{2} .\) similares para\(y=\cos ^{-1} x=\arccos x\) y\(\tan ^{-1} x=\)\(\arctan x .\)
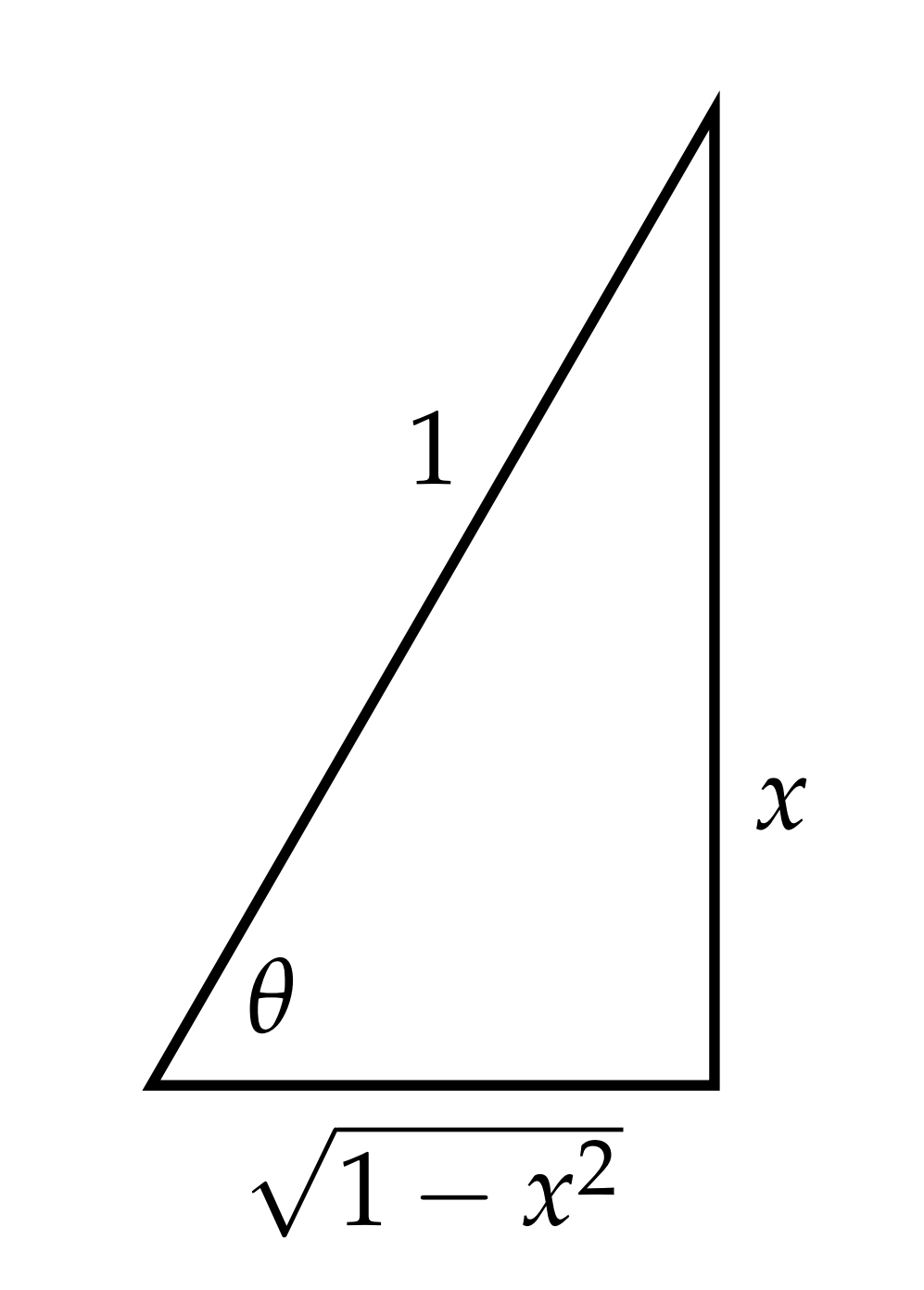
Una vez que piensas en estas funciones como proporcionar ángulos, entonces puedes tener sentido a partir de expresiones de aspecto más complicadas, como\(\tan \left(\sin ^{-1} x\right)\). Tales expresiones suelen aparecer en evaluaciones de integrales. Podemos desenredar esto para producir una forma más simple haciendo referencia a la expresión Ecuación\(\PageIndex{24}\). \(\theta=\sin ^{-1} x\)es simple un ángulo cuyo seno es\(x\). Conociendo el seno es el lado opuesto de un triángulo rectángulo dividido por su hipotenusa, entonces uno simplemente dibuja un triángulo en esta proporción como se muestra en la Figura\(\PageIndex{1}\). A saber, el lado opuesto al ángulo tiene longitud\(x\) y la hipotenusa tiene longitud 1. Usando el Teorema de Pitágoras, el lado faltante (adyacente al ángulo) es simplemente\(\sqrt{1-x^{2}}\). Habiendo obtenido las longitudes para los tres lados, ahora podemos producir la tangente del ángulo como
\[\tan \left(\sin ^{-1} x\right)=\dfrac{x}{\sqrt{1-x^{2}}} \nonumber \]


