1.1:1.1 Revisión del Primer Curso
- Page ID
- 118922
En esta sección revisamos algunas de las técnicas de solución encontradas en un primer curso en ecuaciones diferenciales. No vamos a revisar la teoría básica salvo en posibles referencias como recordatorios de lo que estamos haciendo.
Primero recordamos que una ecuación diferencial ordinaria de orden\(n\) -ésimo es una ecuación para una función desconocida\(y(x)\) que expresa una relación entre la función desconocida y sus primeras\(n\) derivadas. Uno podría escribir esto generalmente como
\[F(y^{(n)}(x),y^{(n-1)}(x),...,y'(x),y(x),x) = 0 \label{1.1} \]
Aquí\(y^{(n)}(x)\) representa el\(n\) th derivado de\(y(x)\).
Un problema de valor inicial consiste en la ecuación diferencial más los valores de las primeras\(n-1\) derivadas a un valor particular de la variable independiente, digamos\(x_0\):
\[y^{(n-1)}(x_0) = y_{n-1}, y^{(n-2)}(x_0) = y_{n-2}, ..., y(x_0) = y_0 \label{1.2} \]
Una ecuación diferencial lineal de orden\(n\) th toma la forma
\[a_n(x)y^{(n)}(x)+a_{n-1}(x)y^{(n-1)}(x)+...+a_1(x)y'(x)+a_0(x)y(x)) = f(x) \label{1.3} \]
Si\(f(x) \equiv 0\), entonces se dice que la ecuación es homogénea, de lo contrario no es homogénea.
1.1.1 Ecuaciones diferenciales de primer orden
Normalmente, las primeras ecuaciones diferenciales encontradas son ecuaciones de primer orden. Una ecuación diferencial de primer orden toma la forma
\[F(y',y,x) = 0 \label{1.4} \]
Existen dos formas generales para las cuales se puede obtener formalmente una solución. El primero es el caso separable y el segundo es una ecuación de primer orden. Indicamos que podemos obtener soluciones formalmente, ya que se puede mostrar la integración necesaria que conduce a una solución. Sin embargo, las integrales resultantes no siempre son reducibles a funciones elementales ni se obtienen soluciones explícitas cuando las integrales son factibles.
Una ecuación de primer orden es separable si se puede escribir la forma
\[\dfrac{dy}{dx} = f(x)g(y) \label{1.5} \]
Los casos especiales resultan cuando cualquiera\(f(x) = 1\) o\(g(y) = 1\). En el primer caso se dice que la ecuación es autónoma.
La solución general a la ecuación (1.5) se obtiene en términos de dos integrales:
\[\int \dfrac{d y}{g(y)}=\int f(x) d x+C \label{1.6} \]
donde C es una constante de integración. Esto produce una familia de soluciones de 1 parámetro a la ecuación diferencial correspondiente a diferentes valores de\(C\). Si uno puede resolver (1.6) para\(y(x)\), entonces se obtiene una solución explícita. De lo contrario, se tiene una familia de soluciones implícitas. Si también se da una condición inicial, entonces uno podría ser capaz de encontrar un miembro de la familia que satisfaga esta condición, que a menudo se llama una solución particular.
Aplicando (1.6), uno tiene
\[\int \dfrac{dy}{y} = \int 2x dx + C. \nonumber \]
Integración de rendimientos
\[\ln |y| = x^2 + C. \nonumber \]
Exponenciando, se obtiene la solución general,
\[y(x)=\pm e^{x^{2}+C}=A e^{x^{2}} \nonumber \]
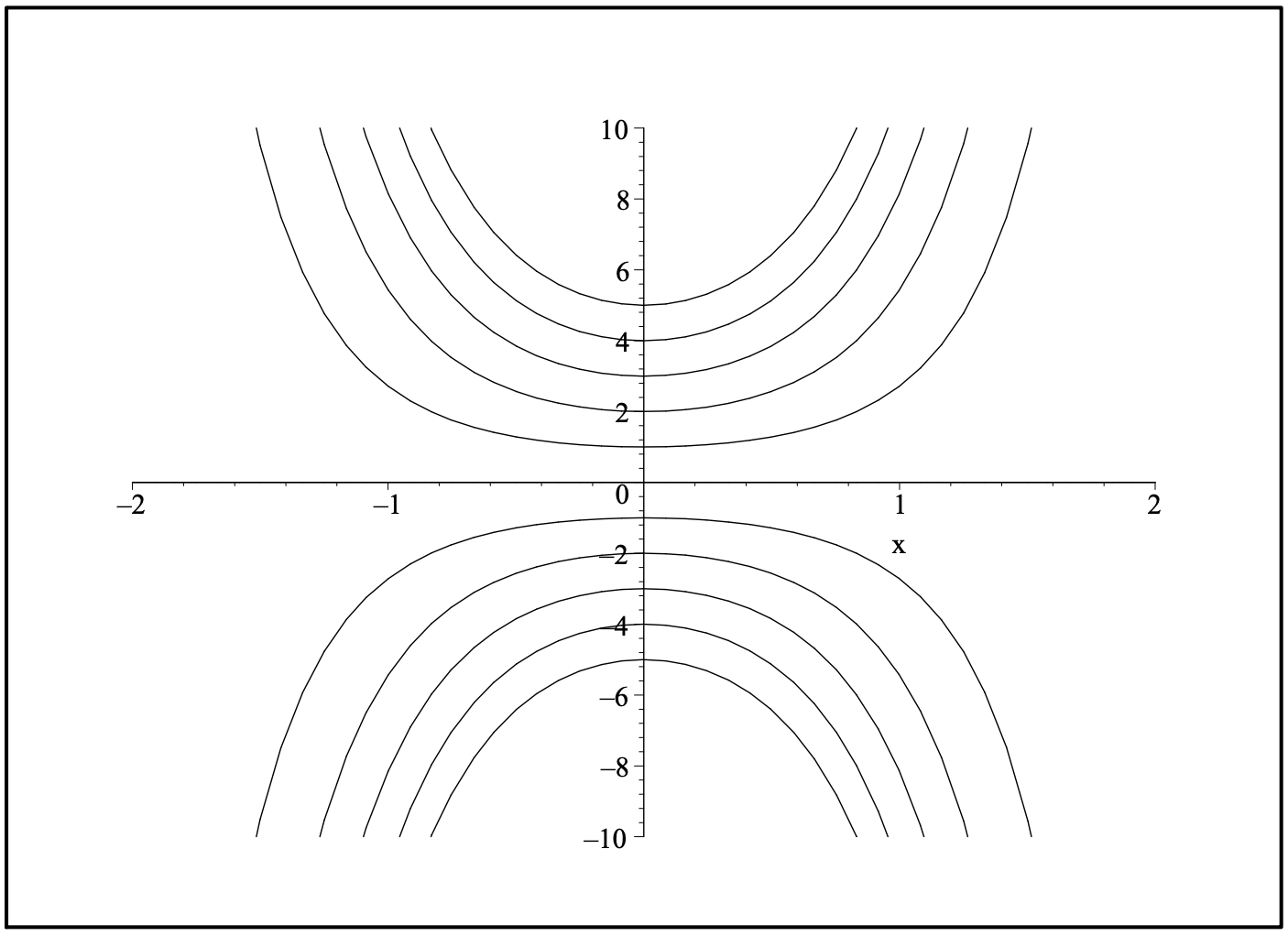
Aquí hemos definido\(A=\pm e^{C}\). Dado que\(C\) es una constante arbitraria,\(A\) es una constante arbitraria. Varias soluciones en esta familia de 1 parámetro se muestran en la Figura 1.1.
A continuación, se busca una solución particular que satisfaga la condición inicial. Porque\(y(0)=2\), uno encuentra eso\(A=2\). Entonces, la solución particular que satisface las condiciones iniciales es\(y(x)=2 e^{x^{2}}\).
Siguiendo el mismo procedimiento que en el último ejemplo, se obtiene:
\[\int y d y=-\int x d x+C \Rightarrow y^{2}=-x^{2}+A, \quad \text { where } \quad A=2 C \nonumber \]
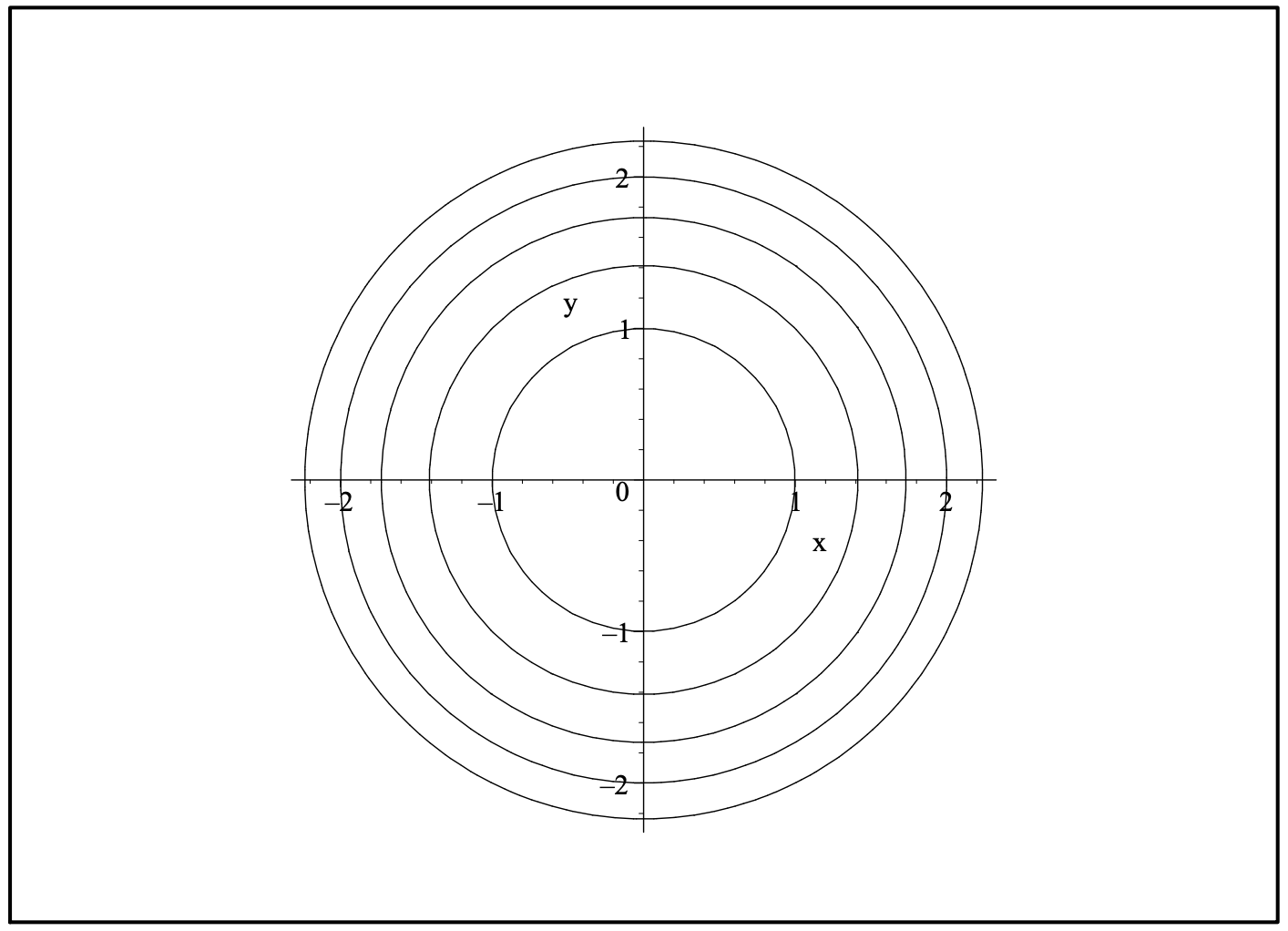
Así, obtenemos una solución implícita. Escribiendo la solución como\(x^2+y^2=A\), vemos que esta es una familia de círculos para\(A > 0\) y el origen para\(A = 0\). Las parcelas de algunas soluciones de esta familia se muestran en la Figura 1.2.
El segundo tipo de ecuación de primer orden encontrado es la ecuación diferencial lineal de primer orden en la forma
\[y'(x) + p(x)y(x) = q(x). \label{1.7} \]
En este caso se busca un factor integrador\(µ(x)\), que es una función que se puede multiplicar a través de la ecuación haciendo del lado izquierdo una derivada perfecta. Así, obtener,
\[\dfrac{d}{dx}[\mu(x)y(x)] = \mu(x)q(x). \label{1.8} \]
El factor integrador que funciona es\(\mu(x)=\exp \left(\int^{x} p(\xi) d \xi\right)\). Se puede mostrar esto expandiendo la derivada en la Ecuación (1.8),
\[\mu(x) y^{\prime}(x)+\mu^{\prime}(x) y(x)=\mu(x) q(x), \label{1.9} \]
y comparando esta ecuación con la obtenida al multiplicar (1.7) por\(\mu(x)\):
\[\mu(x) y^{\prime}(x)+\mu(x) p(x) y(x)=\mu(x) q(x). \label{1.10} \]
Tenga en cuenta que estas dos últimas ecuaciones serían las mismas si
\[\dfrac{d\mu(x)}{dx} = \mu(x)p(x). \nonumber \]
Se trata de una ecuación separable de primer orden cuya solución es la forma dada anteriormente para el factor integrador,
\[\mu(x)=\exp \left(\int^{x} p(\xi) d \xi\right). \label{1.11} \]
La ecuación (1.8) se integra fácilmente para obtener
\[y(x)=\dfrac{1}{\mu(x)}\left[\int^{x} \mu(\xi) q(\xi) d \xi+C\right]. \label{1.12} \]
Uno primero señala que se trata de una ecuación diferencial lineal de primer orden. Resolviendo por $y^ {\ prime} $, se puede ver que la ecuación original no es separable. Sin embargo, no está en la forma estándar. Entonces, primero reescribimos la ecuación como
\[\dfrac{d y}{d x}+\dfrac{1}{x} y=1. \label{1.13} \]
Señalando que\(p(x)=\dfrac{1}{x}\), determinamos el factor integrador
\[\mu(x)=\exp \left[\int^{x} \dfrac{d \xi}{\xi}\right]=e^{\ln x}=x \nonumber \]
Multiplicando la ecuación (1.13) por\(\mu(x) = x\), ¡en realidad recuperamos la ecuación original! En este caso hemos encontrado que\(xy′+y\) debió haber sido el derivado de algo para comenzar. De hecho,\((xy)′ = xy′ + x\). Por tanto, la ecuación (1.8) se convierte en
\[(xy)' = x. \nonumber \]
Integrando uno obtiene
\(xy = \dfrac{1}{2}x^2 + C\),
o
\[y(x) = \dfrac{1}{2}x + \dfrac{C}{x}. \nonumber \]
Insertando la condición inicial en esta solución, tenemos\(0 = \dfrac{1}{2} + C\). Por lo tanto,\(C = -\dfrac{1}{2}\). Así, la solución del problema de valor inicial es\(y(x) = \dfrac{1}{2}(x - \dfrac{1}{x})\).
En realidad, este problema es fácil si te das cuenta de que
\[\dfrac{d}{dx}((\text{sin } x)y) = (\text{sin } x)y' + (\text{cos }x)y. \nonumber \]
Pero, pasaremos por el proceso de encontrar el factor integrador para la práctica.
Primero, reescribe la ecuación diferencial original en forma estándar:
\[y' + (\cot x)y = x^2. \nonumber \]
Luego, compute el factor de integración como
\[\mu(x)=\exp \left(\int^{x} \cot \xi d \xi\right)=e^{-\ln (\sin x)}=\dfrac{1}{\sin x}. \nonumber \]
Usando el factor integrador, la ecuación original se convierte
\[\dfrac{d}{d x}((\sin x) y)=x^{2}. \nonumber \]
Integrando, tenemos
\[y \sin x=\dfrac{1}{3} x^{3}+C. \nonumber \]
Entonces, la solución es
\[y=\left(\dfrac{1}{3} x^{3}+C\right) \csc x. \nonumber \]
Hay otras ecuaciones de primer orden que se pueden resolver para soluciones de forma cerrada. Sin embargo, muchas ecuaciones no son solucionables, o una simplemente está interesada en el comportamiento de las soluciones. En tales casos se gira a campos de dirección. Volveremos a una discusión sobre el comportamiento cualitativo de las ecuaciones diferenciales más adelante en el curso.
1.1.2 Ecuaciones diferenciales lineales de segundo orden
Las ecuaciones diferenciales de segundo orden suelen ser más duras que las de primer orden. En la mayoría de los casos los estudiantes solo están expuestos a ecuaciones diferenciales lineales de segundo orden. Una forma general para una ecuación diferencial lineal de segundo orden viene dada por
\[a(x)y''(x)+b(x)y'(x)+c(x)y(x) = f(x). \label{1.14} \]
Se puede reescribir esta ecuación usando la terminología del operador. A saber, uno primero define el operador diferencial\(L = a(x)D^2 + b(x)D + c(x)\), donde\(D = \dfrac{d}{dx}\). Entonces la ecuación (1.14) se convierte en
\[Ly = f \label{1.15} \]
Las soluciones de ecuaciones diferenciales lineales se encuentran haciendo uso de la linealidad de\(L\). A saber, consideramos el espacio vectorial que consiste en funciones de valor real sobre algún dominio. Dejar\(f\) y\(g\) ser vectores en este espacio de funciones. \(L\)es un operador lineal si para dos vectores\(f\)\(g\) y y escalar\(a\), tenemos que
a.\(L(f+g) = Lf + Lg\)
b.\(L(af) = aLf\)
Normalmente se resuelve (1.14) encontrando la solución general del problema homogéneo,
\[Ly_h = 0 \nonumber \]
y una solución particular del problema no homogéneo,
\[Ly_p = f. \nonumber \]
Entonces la solución general de (1.14) simplemente se da como\(y = y_h + y_p\). Esto es cierto por la linealidad de\(L\). A saber,
\ [\ begin {alineado}
L_y &= L (y_h + y_p)\\
&= Ly_h + Ly_p\\
&= 0 + f = f
\ end {alineado}\ label {1.16}\]
Existen métodos para encontrar una solución particular de una ecuación diferencial. Estos van desde la pura adivinación hasta el Método de Coeficientes Indeterminados, o haciendo uso del Método de Variación de Parámetros. Repasaremos algunos de estos métodos más adelante.
Determinar soluciones al problema homogéneo,\(Ly_h = 0\), no siempre es fácil. Sin embargo, otros han estudiado una variedad de ecuaciones lineales de segundo orden y nos han ahorrado el problema para algunas de las ecuaciones diferenciales que suelen aparecer en aplicaciones.
Nuevamente, la linealidad es útil para producir la solución general de una ecuación diferencial lineal homogénea. Si\(y_1\) y\(y_2\) son soluciones de la ecuación homogénea, entonces la combinación lineal\(y = c_1y_1 + c_2y_2\) es también una solución de la ecuación homogénea. De hecho, si\(y_1\) y\(y_2\) son linealmente independientes, entonces\(y = c_1y_1 + c_2y_2\) es la solución general del problema homogéneo. Como recordarás, la independencia lineal se establece si el Wronskian de las soluciones no es cero. En este caso, tenemos
\[W(y_1,y_2) = y_1(x)y'_2(x) - y'_1(x)y_2(x) \neq 0. \label{1.17} \]
1.1.3 Ecuaciones de Coeficientes Constantes
Las ecuaciones diferenciales de segundo orden más simples y vistas son aquellas con coeficientes constantes. La forma general para una ecuación diferencial lineal de segundo orden de coeficiente constante homogéneo se da como
\[ay''(x) + by'(x) + cy(x) = 0 \label{1.18} \]
donde\(a,b\), y\(c\) son constantes.
Las soluciones a (1.18) se obtienen haciendo una suposición de\(y(x) = e^{rx}\). Insertar esta suposición en (1.18) conduce a la ecuación característica
\[ar^2 + br + c = 0 \label{1.19} \]
Las raíces de esta ecuación a su vez conducen a tres tipos de solución dependiendo de la naturaleza de las raíces como se muestra a continuación.
La ecuación característica para este problema es\(r^2 - r - 6 = 0\). Las raíces de esta ecuación se encuentran como\(r = −2, 3\). Por lo tanto, la solución general se puede anotar rápidamente:
\[y(x) = c_1e^{-2x} + c_2e^{3x}. \nonumber \]
Obsérvese que hay dos constantes arbitrarias en la solución general. Por lo tanto, se necesitan dos piezas de información para encontrar una solución particular. Por supuesto, tenemos la información necesaria en la forma de las condiciones iniciales.
También se necesita evaluar la primera derivada
\[y'(x) = -2c_1e^{-2x} + 3c_2e^{3x} \nonumber \]
a fin de intentar satisfacer las condiciones iniciales. Evaluando\(y\) y\(y′\) en\(x = 0\) rendimientos
\ [\ begin {aligned}
2 &= c_1 + c_2\\
0 &= -2c_1 + 3c_2
\ end {alineado}\ label {1.20}\]
Estas dos ecuaciones en dos incógnitas se pueden resolver fácilmente para dar\(c_1 = 6/5\) y\(c_2 = 4/5\). Por lo tanto, la solución del problema de valor inicial se obtiene como\(y(x) = \dfrac{6}{5}e^{-2x} + \dfrac{4}{5}e^{3x}\).
- Raíces reales y distintas\(r_1, r_2\). En este caso las soluciones correspondientes a cada raíz son linealmente independientes. Por lo tanto, la solución general es simplemente\(y(x) = c_1e^{r_1x} + c_2e^{r_2x}\).
- Raíces reales e iguales\(r_1 = r_2 = r\). En este caso las soluciones correspondientes a cada raíz son linealmente dependientes. Para encontrar una segunda solución linealmente independiente, se utiliza el Método de Reducción del Orden. Esto da la segunda solución como\(xe^{rx}\). Por lo tanto, la solución general se encuentra como\(y(x) = (c_1 + c_2 x)e^{rx}\). [Esto se trata en el apéndice de este capítulo].
- Raíces conjugadas complejas\(r_1, r_2 = \alpha \pm i \beta\). En este caso las soluciones correspondientes a cada raíz son linealmente independientes. Haciendo uso de la identidad de Euler\(e^{i \theta} = \cos(\theta) + i \sin(\theta)\), estos exponenciales complejos pueden ser reescritos en términos de funciones trigonométricas. A saber, uno tiene eso\(e^{\alpha x} \cos(\beta x)\) y\(e^{\alpha x} \sin(\beta x)\) son dos soluciones linealmente independientes. Por lo tanto, la solución general se convierte\(y(x) = e^{\alpha x}(c_1 \cos(\beta x) + c_2 \sin(\beta x))\). [Esto se trata en el apéndice de este capítulo.]
En este ejemplo tenemos\(r^2 + 6r + 9 = 0\). Sólo hay una raíz,\(r=-3\). Nuevamente, la solución se obtiene fácilmente como\(y(x) = (c_1 + c_2 x)e^{-3x}\).
La ecuación característica en este caso es\(r^2 + 4 = 0\). Las raíces son raíces imaginarias puras,\(r \pm 2i\) y la solución general consiste puramente en funciones sinusoidales:\(y(x) = c_1 \cos(2x) + c_2 \sin(2x)\).
La ecuación característica en este caso es\(r^2 + 2r + 4 = 0\). Las raíces son complejas,\(r = -1 \pm \sqrt{3}i \) y la solución general se puede escribir como\(y(x) = [c_1 \cos(\sqrt{3}x) + c_2 \sin(\sqrt{3}x)] e^{-x}\).
Una de las aplicaciones más importantes de las ecuaciones en los dos últimos ejemplos es en el estudio de las oscilaciones. Los sistemas típicos son una masa en un resorte, o un simple péndulo. Para una masa\(m\) en un resorte con constante de resorte\(k > 0\), se tiene de la ley de Hooke que la posición en función del tiempo\(x(t)\),, satisface la ecuación
\[mx'' + kx = 0. \nonumber \]
Esta ecuación de coeficiente constante tiene raíces imaginarias puras (\(\alpha = 0\)) y las soluciones son senos y cosenos puros. Tal movimiento se llama movimiento armónico simple.
Agregar un término de amortiguación y forzamiento periódico complica la dinámica, pero no obstante es solucionable. El siguiente ejemplo muestra un oscilador armónico forzado.
Este es un ejemplo de un problema no homogéneo. El problema homogéneo se resolvió realmente en el Ejemplo 1.7. Según la teoría, solo necesitamos buscar una solución particular al problema no homogéneo y agregarlo a la solución del último ejemplo para obtener la solución general.
La solución particular se puede obtener simplemente adivinando, haciendo una suposición educada o usando el Método de Variación de Parámetros. No vamos a revisar todas estas técnicas en este momento. Debido a la forma simple del término de manejo, haremos una suposición inteligente\(y_p(x) = A \sin x\) y determinaremos lo que\(A\) debe ser. Recordemos, este es el Método de Coeficientes Indeterminados que revisamos en la siguiente sección. Insertar nuestra conjetura en la ecuación da\((−A + 4A) \sin x = \sin x\). Entonces, vemos que\(A = 1/3\) funciona. Por lo tanto, la solución general del problema no homogéneo es\(y(x) = c_1 \cos(2x) + c_2 \sin(2x) + \dfrac{1}{3} \sin x\).
1.1.4 Método de Coeficientes Indeterminados
A la fecha, sólo sabemos resolver coeficientes constantes, ecuaciones homogéneas. ¿Cómo se resuelve una ecuación no homogénea como esa en la Ecuación (1.14)?
\[a(x)y''(x) + b(x)y'(x) + c(x)y(x) = f(x) \label{1.21} \]
Recordemos, que se resuelve esta ecuación encontrando la solución general del problema homogéneo,
\[Ly_h = 0 \nonumber \]
y una solución particular del problema no homogéneo,
\[Ly_p = f. \nonumber \]
Entonces la solución general de (1.14) simplemente se da como\(y = y_h + y_p\). Entonces, ¿cómo encontramos la solución particular?
Se podría adivinar una solución, pero eso no suele ser posible sin un poco de experiencia. Entonces necesitamos algunos otros métodos. Hay dos métodos principales. En el primer caso, el Método de Coeficientes Indeterminados, se hace una suposición inteligente basada en la forma de\(f(x)\). En el segundo método, uno puede desarrollar sistemáticamente la solución particular. Volveremos a este método el Método de Variación de Parámetros, más adelante en el libro.
Resolvamos una ecuación diferencial simple destacando cómo podemos manejar ecuaciones no homogéneas.
\[y'' + 2y' - 3y = 4 \label{1.22} \]
El primer paso es determinar la solución de la ecuación homogénea.
Así, resolvemos
\[y_h^{''} + 2y_h^{'} - 3y_h = 0 \label{1.23} \]
La ecuación característica es\(r^2 + 2r - 3 = 0\). Las raíces son\(r = 1, -3\). Entonces, podemos escribir inmediatamente la solución
\[y_h(x) = c_1e^x + c_2e^{-3x}. \nonumber \]
El segundo paso es encontrar una solución particular de (1.22). ¿Qué función posible podemos insertar en esta ecuación de tal manera que solo quede un 4? Si intentamos algo proporcional a\(x\), entonces nos quedamos con una función lineal después de insertar\(x\) y sus derivadas. Quizás una función constante se podría pensar. \(y = 4\)no funciona. Pero, podríamos intentar una constante arbitraria,\(y = A\).
A ver. \(y = A\)Insertando en (1.22), obtenemos
\[-3A = 4. \nonumber \]
¡Ah, ja! Vemos que podemos elegir\(A = -\dfrac{4}{3}\) y esto funciona. Entonces, tenemos una solución particular\(y_p(x) = -\dfrac{4}{3}\). Este paso está hecho.
Combinando nuestras dos soluciones, tenemos la solución general a la ecuación original no homogénea (1.22). A saber,
\[y(x) = y_h(x) + y_p(x) = c_1e^x + c_2e^{-3x} - \dfrac{4}{3}. \nonumber \]
Inserte esta solución en la ecuación y verifique que efectivamente sea una solución. Si se nos hubieran dado condiciones iniciales, ahora podríamos utilizarlas para determinar nuestras constantes arbitrarias.
¿Y si tuviéramos un término fuente diferente? Considera la ecuación
\[y'' +2y' - 3y = 4x \label{1.24} \]
Lo único que cambiaría es nuestra solución particular. Entonces, necesitamos una conjetura.
Sabemos que una función constante no funciona por el último ejemplo. Entonces, intentemos\(y_p = Ax\). Insertando esta función en la ecuación (?? ), obtenemos
\[2A - 3Ax = 4x. \nonumber \]
Picking\(A = -4/3\) se desharía de los\(x\) términos, pero no lo cancelará todo. Todavía tenemos una izquierda constante. Entonces, necesitamos algo más general.
Probemos una función lineal,\(y_p(x) = Ax + B\). Luego obtenemos después de la sustitución en (1.24)
\[2A - 3(Ax + B) = 4x. \nonumber \]
Igualando los coeficientes de las diferentes potencias de ambos\(x\) lados, encontramos un sistema de ecuaciones para los coeficientes indeterminados:
\ [\ begin {alineado}
2A - 3B &= 0\\
-3A &= 4
\ end {alineado}\ etiqueta {1.25}\]
Estos se resuelven fácilmente para obtener
\ [\ begin {alineado}
A &= -\ dfrac {4} {3}\\
B &=\ dfrac {2} {3} A = -\ dfrac {8} {9}.
\ end {alineado}\ etiqueta {1.26}\]
Entonces, nuestra solución particular es
\[y_p(x) = -\dfrac{4}{3}x - \dfrac{8}{9}. \nonumber \]
Esto da la solución general al problema no homogéneo como
\[y(x) = y_h(x) + y_p(x) = c_1e^x + c_2e^{-3x} - \dfrac{4}{3}x - \dfrac{8}{9}. \nonumber \]
Hay formas generales que puedes adivinar con base en la forma del término de conducción,\(f(x)\). Algunos ejemplos se dan en el Cuadro 1.1.4. Aplicaciones más generales están cubiertas en un texto estándar sobre ecuaciones diferenciales. No obstante, el procedimiento es sencillo. Dado\(f(x)\) en una forma particular, haces una conjetura apropiada hasta algunos parámetros desconocidos, o coeficientes. Insertar la conjetura conduce a un sistema de ecuaciones para los coeficientes desconocidos. Resuelve el sistema y tienes tu solución. Esta solución se agrega luego a la solución general de la ecuación diferencial homogénea.
| \(f(x)\) | Adivina |
|---|---|
| \ (f (x)\) ">
\(a_nx^n + a_{n-1}x^{n-1} + \cdots + a_1x + a_0\) \(ae^{bx}\) \(a \cos wx = b \sin wx\) |
\(A_nx^n + A_{n-1}x^{n-1} + \cdots + A_1x + A_0\) \(Ae^{bx}\) \(A \cos wx + B \sin wx\) |
\[y'' + 2y' - 3y = 2e^{-3x}. \label{1.27} \]
De acuerdo con lo anterior, adivinaríamos una solución de la forma\(y_p = Ae^{-3x}\).
Insertando nuestra suposición, encontramos
\[0 = 2e^{-3x}. \nonumber \]
¡Uy! ¡El coeficiente,\(A\), desapareció! No podemos resolverlo. ¿Qué salió mal?
La respuesta está en la solución general del problema homogéneo. Tenga en cuenta que\(e^x\) y\(e^{-3x}\) son soluciones al problema homogéneo. Entonces, un múltiplo de no nos\(e^{-3x}\) llevará a ningún lado. Resulta que hay una modificación más del método. Si nuestro término de conducción contiene términos que son soluciones del problema homogéneo, entonces necesitamos hacer una conjetura consistente en la menor potencia posible de\(x\) veces la función que ya no es una solución del problema homogéneo. A saber, adivinamos\(y_p(x) = Axe^{-3x}\). Calculamos la derivada de nuestra conjetura,\(y'_p = A(1-3x)e^{-3x}\) y\(y_p^{''} = A(9x - 6)e^{-3x}\). Insertando estos en la ecuación, obtenemos
\([(9x - 6) + 2(1 - 3x) - 3x]Ae^{-3x} = 2e^{-3x}\),
o
\[-4A = 2. \nonumber \]
Entonces,\(A = -1/2\) y\(y_p(x) = -\dfrac{1}{2}xe^{-3x}\).
En general, si algún término en la conjetura\(y_p(x)\) es una solución de la ecuación homogénea, entonces multiplique la conjetura por\(x^k\), donde\(k\) está el entero positivo más pequeño tal que ningún término in\(x^ky_p(x)\) es una solución del problema homogéneo.
1.1.5 Ecuaciones de Cauchy-Euler
Otra clase de ecuaciones diferenciales lineales solucionables que es de interés son las ecuaciones de tipo Cauchy-Euler. Estos son dados por
\[ax^2y''(x) + bxy'(x) + cy(x) = 0. \label{1.28} \]
Obsérvese que en tales ecuaciones la potencia de\(x\) en cada uno de los coeficientes coincide con el orden de la derivada en ese término. Estas ecuaciones se resuelven de manera similar a las ecuaciones de coeficiente constante.
Uno comienza por hacer la conjetura\(y(x) = x^r\). Insertando esta función y sus derivadas,
\(y'(x) = rx^{r-1}, \quad y''(x) = r(r-1)x^{r-2}\),
en la Ecuación (1.28), tenemos
\[[ar(r-1) + br + c]x^r = 0. \nonumber \]
Como esto tiene que ser cierto para todos\(x\) en el dominio del problema, obtenemos la ecuación característica
\[ar(r-1) + br + c = 0. \label{1.29} \]
Al igual que la ecuación diferencial de coeficiente constante, tenemos una ecuación cuadrática y la naturaleza de las raíces vuelve a conducir a tres clases de soluciones. Estos se muestran a continuación. Algunos de los detalles se proporcionan en la siguiente sección.
- Raíces reales y distintas\(r_1, r_2\). En este caso las soluciones correspondientes a cada raíz son linealmente independientes. Por lo tanto, la solución general es simplemente\(y(x) = c_1x^{r_1} + c_2x^{r_2}\).
- Raíces reales e iguales\(r_1 = r_2 = r\). En este caso las soluciones correspondientes a cada raíz son linealmente dependientes. Para encontrar una segunda solución linealmente independiente, se utiliza el Método de Reducción del Orden. Esto da la segunda solución como\(x^r \ln|x|\). Por lo tanto, la solución general se encuentra como\(y(x) = (c_1 + c_2 \ln|x|)x^r\).
- Raíces conjugadas complejas\(r_1,r_2 = \alpha \pm i \beta\). En este caso las soluciones correspondientes a cada raíz son linealmente independientes. Estos exponenciales complejos pueden ser reescritos en términos de funciones trigonométricas. A saber, uno tiene eso\(x^{\alpha} \cos(\beta \ln|x|)\) y\(x^{\alpha} \sin(\beta \ln|x|)\) son dos soluciones linealmente independientes. Por lo tanto, la solución general se convierte\(y(x) = x^{\alpha}(c_1 \cos(\beta \ln|x|) + c_2 \sin(\beta \ln|x|))\).
Al igual que con las ecuaciones de coeficiente constante, comenzamos por anotar la ecuación carcaterística. Haciendo un simple cálculo,
\ [\ begin {alineado}
0 &= r (r-1) + 5r + 12\\
&= r^2 + 4r + 12\\
&= (r+2) ^2 + 8,\\
-8 &= (r+2) ^2,\ end {alineado}\ etiqueta {1.30}\]
uno determina que las raíces son\(r = -2 \pm 2 \sqrt{2}i\). Por lo tanto, la solución general es\(y(x) = [c_1 \cos(2 \sqrt{2} \ln|x|) + c_2 \sin(2\sqrt{2} \ln|x|)]x^{-2}\)
Para este ejemplo la ecuación característica toma la forma
\(r(r-1)+3 r+1=0\),
o
\[r^{2}+2 r+1=0. \nonumber \]
Sólo hay una raíz real,\(r=-1\). Por lo tanto, la solución general es
\[y(t)=\left(c_{1}+c_{2} \ln |t|\right) t^{-1} \nonumber \]
Sin embargo, este problema es un problema de valor inicial. En\(t=1\) conocemos los valores de\(y\) y\(y^{\prime}\). Usando la solución general, primero tenemos eso
\[0=y(1)=c_{1} \nonumber \]
Así, tenemos hasta el momento eso\(y(t)=c_{2} \ln |t| t^{-1}\). Ahora, usando la segunda condición y
\[y^{\prime}(t)=c_{2}(1-\ln |t|) t^{-2} \nonumber \]
tenemos
\[1=y(1)=c_{2}. \nonumber \]
Por lo tanto, la solución del problema de valor inicial es\(y(t)=\ln |t| t^{-1}\).
Ecuaciones de Cauchy-Euler no homogéneas
También podemos resolver algunas ecuaciones no homogéneas de Cauchy-Euler utilizando el Método de Coeficientes Indeterminados. Demostraremos esto con un par de ejemplos.
Primero encontramos la solución de la ecuación homogénea. La ecuación característica es\(r^{2}-2 r-3=0\). Entonces, las raíces son\(r=-1,3\) y la solución es\(y_{h}(x)=c_{1} x^{-1}+c_{2} x^{3}\).
A continuación necesitamos una solución particular. Vamos a adivinar\(y_{p}(x)=A x^{2}\). Insertando la conjetura en la ecuación diferencial no homogénea, tenemos
\ [\ begin {alineado}
2 x^ {2} &=x^ {2} y^ {\ prime\ prime} -x y^ {\ prime} -3 y=2 x^ {2}\\
&=2 A x^ {2} -2 A x^ {2} -3 A x^ {2}\
&=-3 A x^ {2}
\ end {alineado}\ etiqueta {1.31}\]
Entonces,\(A=-2 / 3\). Por lo tanto, la solución general del problema es
\[y(x)=c_{1} x^{-1}+c_{2} x^{3}-\dfrac{2}{3} x^{2}. \nonumber \]
En este caso el término no homogéneo es una solución del problema homogéneo, que resolvimos en el último ejemplo. Entonces, necesitaremos una modificación del método. Tenemos un problema de la forma
\[a x^{2} y^{\prime \prime}+b x y^{\prime}+c y=d x^{r} \nonumber \]
donde\(r\) es una solución de\(a r(r-1)+b r+c=0\). Adivina una solución de la forma\(y=A x^{r} \ln x\). Entonces uno encuentra que la ecuación diferencial se reduce a\(A x^{r}(2 a r-a+b)=d x^{r}\). [Debes verificar esto por ti mismo.]
Con esto en mente, ahora podemos resolver el problema que nos ocupa. Vamos\(y_{p}= A x^{3} \ln x\). Insertando en la ecuación, obtenemos\(4 A x^{3}=2 x^{3}\), o\(A=1 / 2\). La solución general del problema ahora puede escribirse como
\[y(x)=c_{1} x^{-1}+c_{2} x^{3}+\dfrac{1}{2} x^{3} \ln x \nonumber \]


