2.2: Soluciones de equilibrio y comportamientos cercanos
- Page ID
- 118907
Al estudiar sistemas de ecuaciones diferenciales, suele ser útil estudiar el comportamiento de las soluciones sin obtener una forma algebraica para la solución. Esto se hace explorando soluciones de equilibrio y soluciones cercanas a soluciones de equilibrio. Dichas técnicas se verán útiles posteriormente en el estudio de sistemas no lineales.
Comenzamos esta sección estudiando soluciones de equilibrio de sistema (2.4). Para soluciones de equilibrio el sistema no cambia en el tiempo. Por lo tanto, las soluciones de equilibrio satisfacen las ecuaciones\(x^{\prime}=0\) y\(y^{\prime}=0\). Por supuesto, esto sólo puede suceder para soluciones constantes. Dejar\(x_{0}\) y\(y_{0}\) ser las soluciones de equilibrio (constante). Entonces,\(x_{0}\) y\(y_{0}\) debe satisfacer el sistema
\ [\ begin {alineado}
&0=a x_ {0} +b y_ {0} +e,\\
&0=c x_ {0} +d y_ {0} +f.
\ final {alineado}\ etiqueta {2.15}\]
Este es un sistema lineal de ecuaciones algebraicas no homogéneas. Uno solo tiene una solución única cuando el determinante del sistema no es cero, es decir,\(a d-b c \neq 0\). Usando la regla (determinante) de Cramer para resolver tales sistemas, tenemos
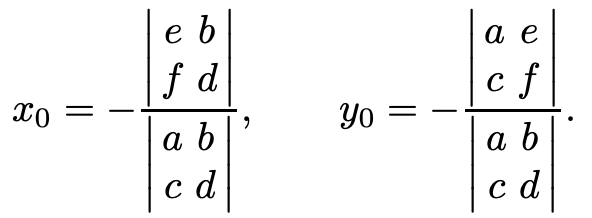
Si el sistema es homogéneo\(e=f=0\), entonces tenemos que el origen es la solución de equilibrio; es decir,\(\left(x_{0}, y_{0}\right)=(0,0)\). Muchas veces tendremos este caso ya que siempre se puede hacer un cambio de coordenadas de\((x, y)\) a\((u, v)\) por\(u=x-x_{0}\) y\(v=y-y_{0}\). Entonces,\(u_{0}=v_{0}=0\).
A continuación nos interesa el comportamiento de las soluciones cercanas a las soluciones de equilibrio. Posteriormente este comportamiento será útil para analizar sistemas no lineales más complicados. Veremos algunos sistemas simples que se resuelven fácilmente.
Considerar el sistema
\ [\ begin {array} {r}
x^ {\ prime} =-2 x\\
y^ {\ prime} =-y.
\ end {array}\ label {2.17}\]
Se trata de un sencillo sistema desacoplado. Cada ecuación se resuelve simplemente para dar
\[x(t)=c_{1} e^{-2 t} \text { and } y(t)=c_{2} e^{-t} \nonumber \]
En este caso vemos que todas las soluciones tienden hacia el punto de equilibrio,\((0,0)\).
Esto se llamará nodo estable, o sumidero.
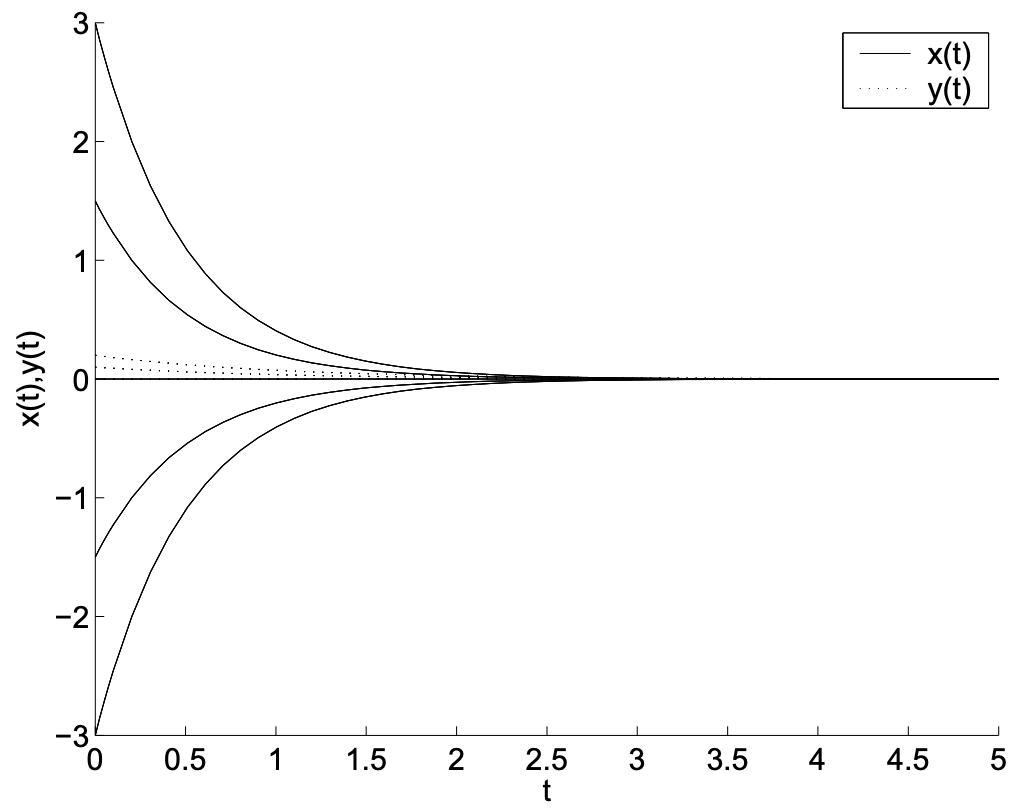
Antes de mirar otro tipo de soluciones, exploraremos el nodo estable en el ejemplo anterior. Existen varios métodos para observar el comportamiento de las soluciones. Podemos observar las gráficas de solución de las variables dependientes versus las independientes, o podemos mirar en el\(x y\) plano -las curvas paramétricas\((x(t), y(t))\).
Gráficas de solución: Se puede trazar cada solución en función de un conjunto\(t\) dado de condiciones iniciales. En la Figura 2.1 se muestran ejemplos para varias condiciones iniciales. Tenga en cuenta que las soluciones decaen para grandes\(t\). Resultados de casos especiales para diversas condiciones iniciales. Tenga en cuenta que para\(t=0, x(0)=c_{1}\) y\(y(0)=c_{2}\). (Por supuesto, uno puede proporcionar condiciones iniciales en cualquier\(t=t_{0}\). Por lo general, es más fácil elegir\(t=0\) nuestras explicaciones generales). Si elegimos una condición inicial con\(c_{1}=0\), entonces\(x(t)=0\) para todos\(t\). Se obtienen resultados similares al configurar\(y(0)=0\).
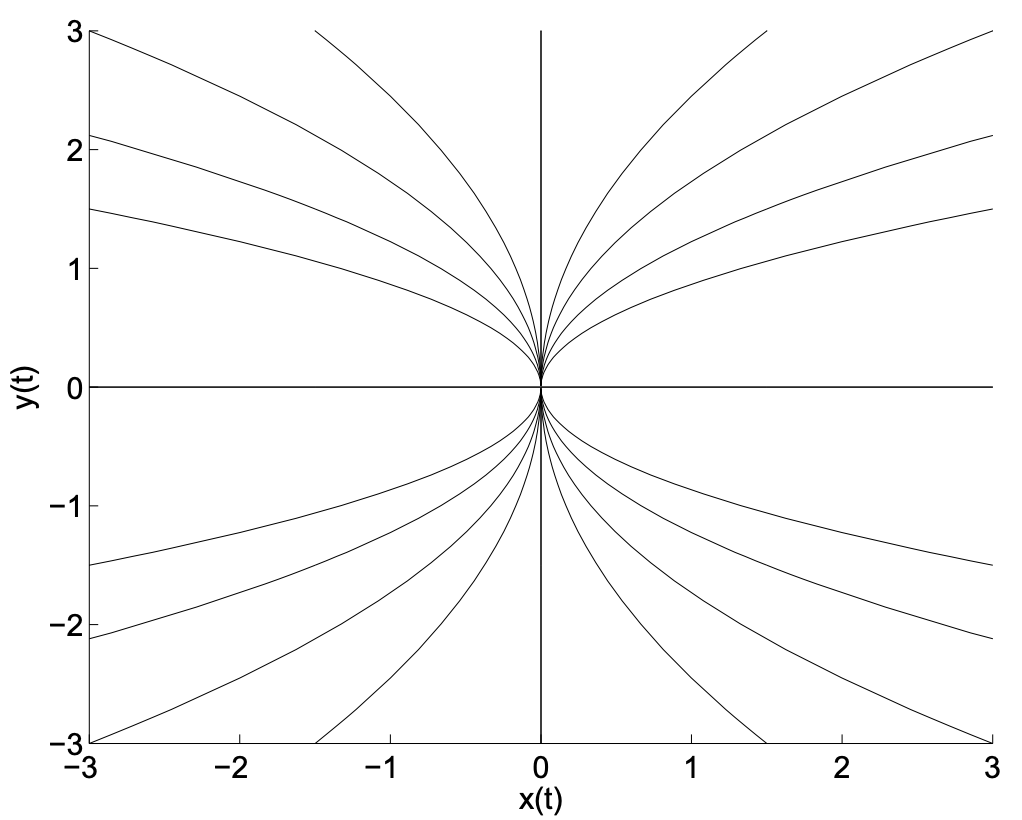
Retrato de fase: Hay otros tipos de parcelas que pueden proporcionar información adicional sobre nuestras soluciones incluso si no podemos encontrar las soluciones exactas como podemos para estos simples ejemplos. En particular, se pueden considerar las soluciones\(x(t)\) y\(y(t)\) como las coordenadas a lo largo de una trayectoria parametrizada, o curva, en el plano:\(\mathbf{r}=(x(t), y(t))\) Tales curvas se denominan trayectorias u órbitas. El\(x y\) -plano se llama plano de fase y una colección de tales órbitas da un retrato de fase para la familia de soluciones del sistema dado.
Un método para determinar las ecuaciones de las órbitas en el plano de fase es eliminar el parámetro\(t\) entre las soluciones conocidas para obtener una relación entre\(x\) y\(y\). En el ejemplo anterior podemos hacer esto, ya que se conocen las soluciones. En particular, tenemos
\[x=c_{1} e^{-2 t}=c_{1}\left(\dfrac{y}{c_{2}}\right)^{2} \equiv A y^{2} \nonumber \]
Otra forma de obtener información sobre las órbitas proviene de señalar que las pendientes de las órbitas en el\(x y\) plano están dadas por\(dy / dx\). Para sistemas autónomos, podemos escribir esta pendiente solo en términos de\(x\) y\(y\). Esto conduce a una ecuación diferencial de primer orden, que posiblemente podría resolverse analíticamente, resolverse numéricamente o simplemente usarse para producir un campo de dirección. Veremos que los campos de dirección son útiles para determinar comportamientos cualitativos de las soluciones sin encontrar soluciones explícitas.
Primero obtendremos las órbitas para el Ejemplo 2.3 resolviendo la ecuación de pendiente correspondiente. Primero, recordemos que para trayectorias definidas paramétricamente por\(x=x(t)\) y\(y=y(t)\), tenemos de la Regla de Cadena para\(y=y(x(t))\) eso
\[\dfrac{dy}{dt} = \dfrac{dy}{dx} \dfrac{dx}{dt}. \nonumber \]
Por lo tanto,
\[\dfrac{dy}{dx} = \dfrac{\dfrac{dy}{dt}}{\dfrac{dx}{dt}} \label{2.18} \]
Para el sistema en (2.17) utilizamos la Ecuación (2.18) para obtener la ecuación para la pendiente en un punto de la órbita:
\[\dfrac{dy}{dx} = \dfrac{y}{2x} \nonumber \]
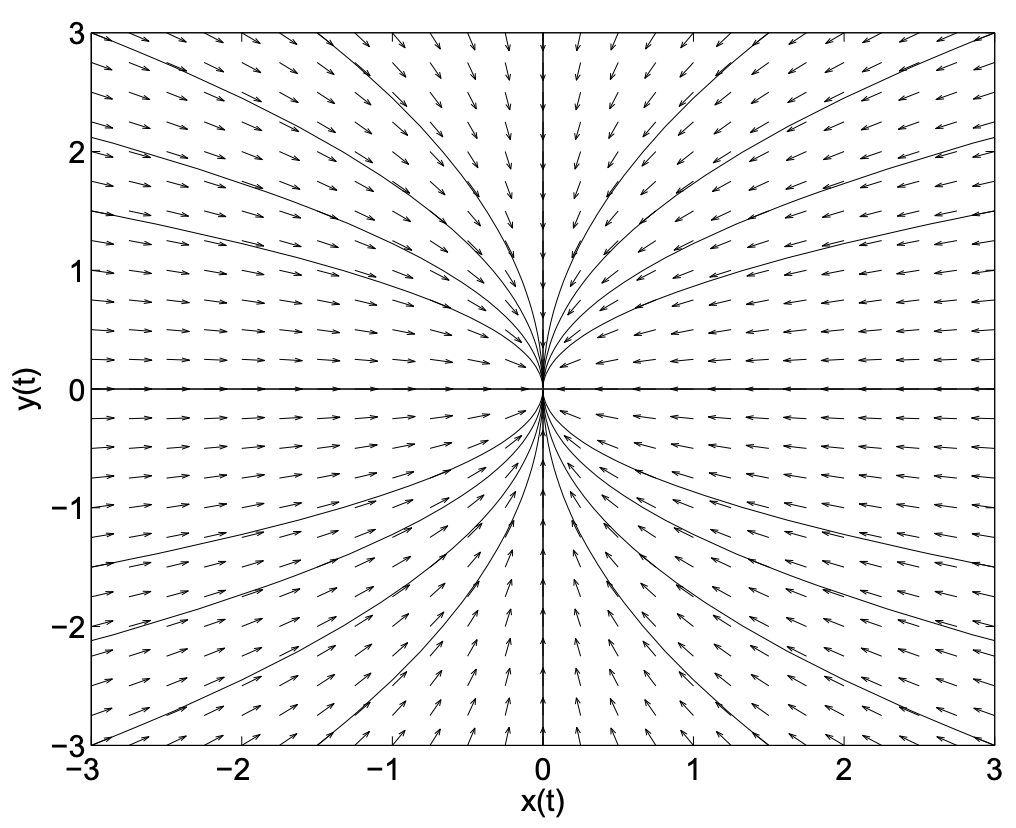
La solución general de esta ecuación diferencial de primer orden se encuentra utilizando la separación de variables como\(x = Ay^2\) para\(A\) una constante arbitraria. Las gráficas de estas soluciones en el plano de fase se dan en la Figura 2.2. [Tenga en cuenta que esta es la misma forma para las órbitas que habíamos obtenido anteriormente al eliminar\(t\) de la solución del sistema. \
Una vez que se tienen soluciones a las ecuaciones diferenciales, a menudo nos interesa el comportamiento a largo plazo de las soluciones. Dada una condición inicial particular\((x_0, y_0)\), ¿cómo se comporta la solución a medida que aumenta el tiempo? Para órbitas cercanas a una solución de equilibrio, ¿las soluciones tienden hacia, o alejándose de, el punto de equilibrio? La respuesta es obvia cuando uno tiene las soluciones exactas\(x(t)\) y\(y(t)\). No obstante, no siempre es así.
Consideremos el ejemplo anterior para las condiciones iniciales en el primer cuadrante del plano de fase. Por un punto en el primer cuadrante tenemos que
\(d x / d t=-2 x<0\),
lo que significa que como\(t \rightarrow \infty, x(t)\) obtener más negativo. Del mismo modo,
\[d y / d t=-y<0 \nonumber \]
indica que también\(y(t)\) se está haciendo más pequeño para este problema. Así, estas órbitas tienden hacia el origen como\(t \rightarrow \infty\). Esta información cualitativa se obtuvo sin depender de las soluciones conocidas al problema.
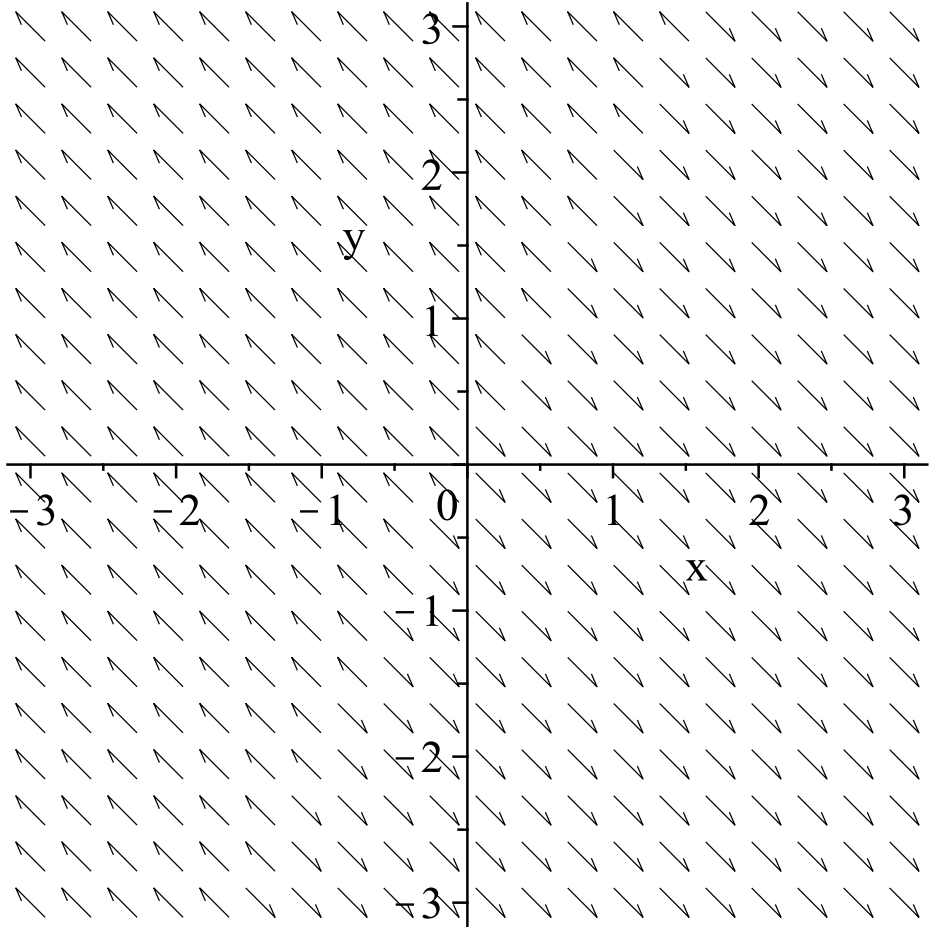
Campos de dirección: Otra forma de determinar el comportamiento de nuestro sistema es dibujar el campo de dirección. Recordemos que un campo de dirección es un campo vectorial en el que se trazan flechas en la dirección de tangentes a las órbitas. Esto se hace porque las pendientes de las líneas tangentes están dadas por\(d y / d x\). Para nuestro sistema (2.5), la pendiente es
\[\dfrac{d y}{d x}=\dfrac{a x+b y}{c x+d y} \nonumber \]
En general, para sistemas no autónomos, obtenemos una ecuación diferencial de primer orden de la forma
\[\dfrac{d y}{d x}=F(x, y) \nonumber \]
Esta ecuación particular puede ser resuelta por el lector. Ver problema de tareas 2.2.
Podemos usar software para dibujar campos de dirección. Sin embargo, uno puede bosquejar estos campos a mano. Tenemos que la pendiente de la tangente en este punto viene dada por
\[\dfrac{d y}{d x}=\dfrac{-y}{-2 x}=\dfrac{y}{2 x} \nonumber \]
Por cada punto del plano se dibuja un trozo de línea tangente con esta pendiente. En la Figura 2.3 mostramos algunos de estos. Para\((x, y)=(1,1)\) la pendiente es\(d y / d x=1 / 2\). Entonces, dibujamos una flecha con pendiente\(1 / 2\) en este punto. Del sistema (2.17), tenemos eso\(x^{\prime}\) y ambos\(y^{\prime}\) son negativos en este punto. Por lo tanto, el vector apunta hacia abajo y hacia la izquierda.
Podemos hacer esto por varios puntos, como se muestra en la Figura 2.3. En ocasiones se pueden esbozar rápidamente vectores con la misma pendiente. Para este ejemplo, cuando\(y=0\), la pendiente es cero y cuando\(x=0\) la pendiente es infinita. Entonces, se pueden proporcionar varios vectores. Dichos vectores son tangentes a curvas conocidas como isoclinas en las que son\(\dfrac{d y}{d x}=\) constantes.
A menudo es difícil proporcionar un boceto preciso de un campo de dirección. El software de computadora se puede utilizar para proporcionar una mejor interpretación. Para el Ejemplo 2.3 se muestra el campo de dirección en la Figura 2.4. Mirando este campo de dirección, se puede comenzar a “ver” las órbitas siguiendo los vectores tangentes.
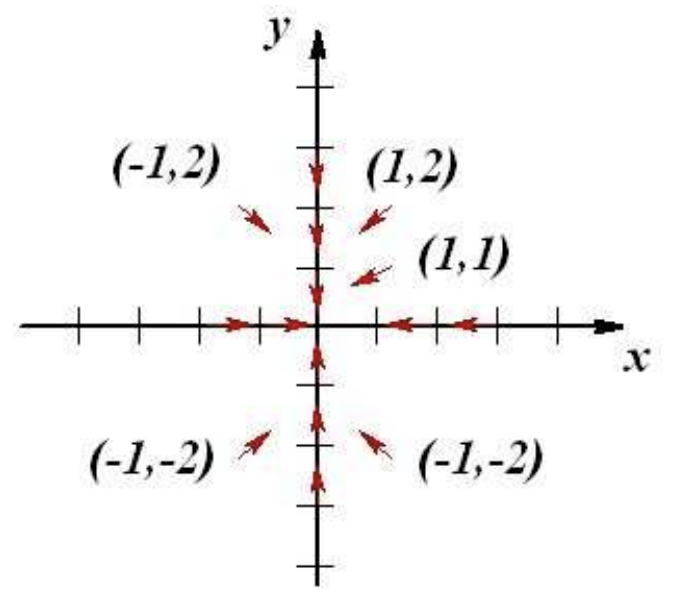
Figura 2.3. Un boceto de varios vectores tangentes para el Ejemplo 2.3.
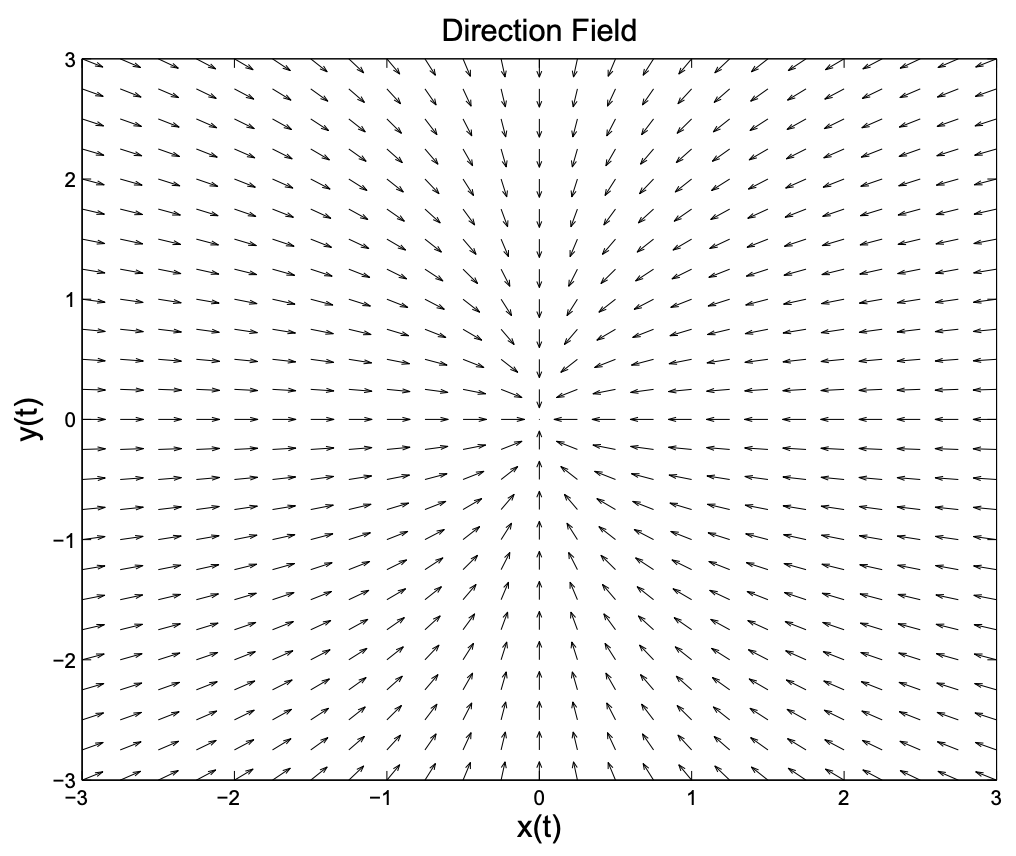
Por supuesto, se pueden superponer las órbitas en el campo de dirección. Esto se muestra en la Figura 2.5. ¿Son estos los patrones que viste en la Figura 2.4?
En este ejemplo vemos que todas las órbitas “fluyen” hacia el origen, o punto de equilibrio. Nuevamente, este es un ejemplo de lo que se llama un nodo estable o un sumidero. (Imagínese lo que le sucede al agua en un fregadero cuando el desagüe está desenchufado).
Considerar el sistema
\[x' = -x \nonumber \]
\[y'=y \label{2.19} \]
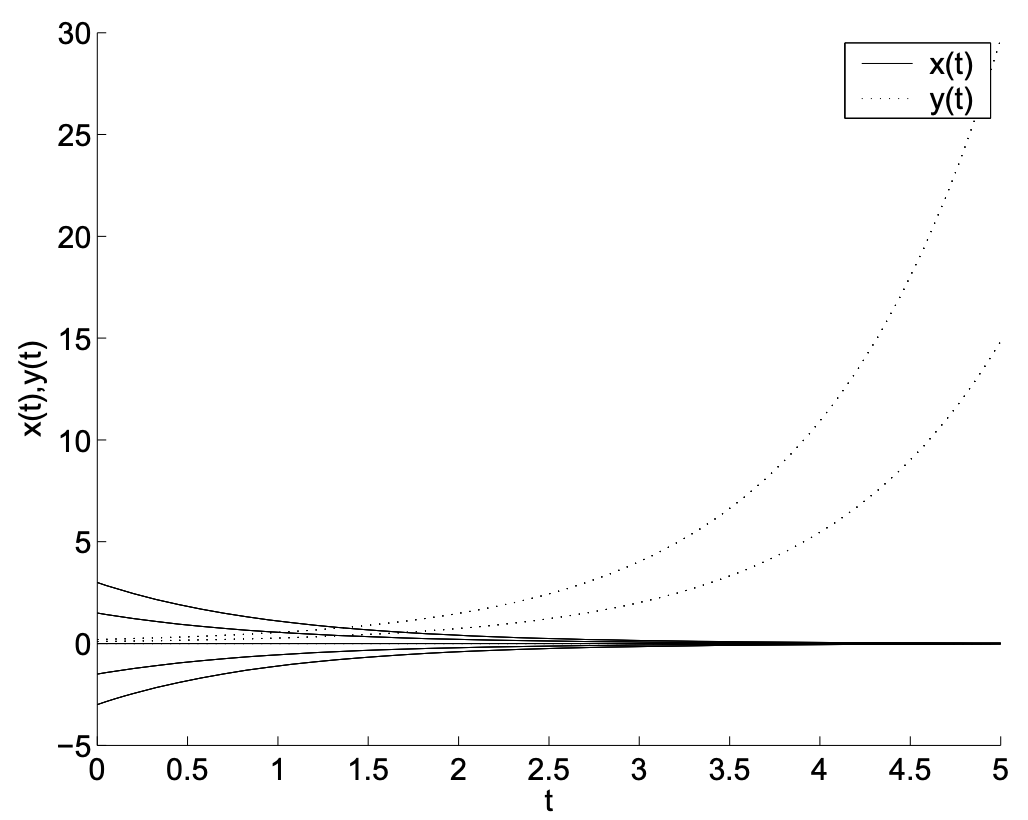
Este es otro sistema desacoplado. Las soluciones se obtienen de nuevo simplemente por integración. Tenemos eso\(x(t)=c_{1} e^{-t}\) y\(y(t)=c_{2} e^{t}\). Aquí tenemos que\(x\) decae a medida que\(t\) se hace grande y\(y\) aumenta a medida que\(t\) se agranda. En particular, si uno recoge las condiciones iniciales con\(c_{2}=0\), entonces las órbitas siguen el\(x\) eje -hacia el origen. Para los puntos iniciales con\(c_{1}=0\), las órbitas que se originan en el\(y\) eje -fluirán alejándose del origen. Por supuesto, en estos casos el origen es un punto de equilibrio y una vez en equilibrio, uno permanece ahí.
De hecho, sólo hay una línea sobre la que escoger las condiciones iniciales de tal manera que la órbita conduzca hacia el punto de equilibrio. No importa lo pequeño\(c_{2}\) que sea, tarde o temprano, el término de crecimiento exponencial dominará la solución. Se puede ver este comportamiento en la Figura 2.6.
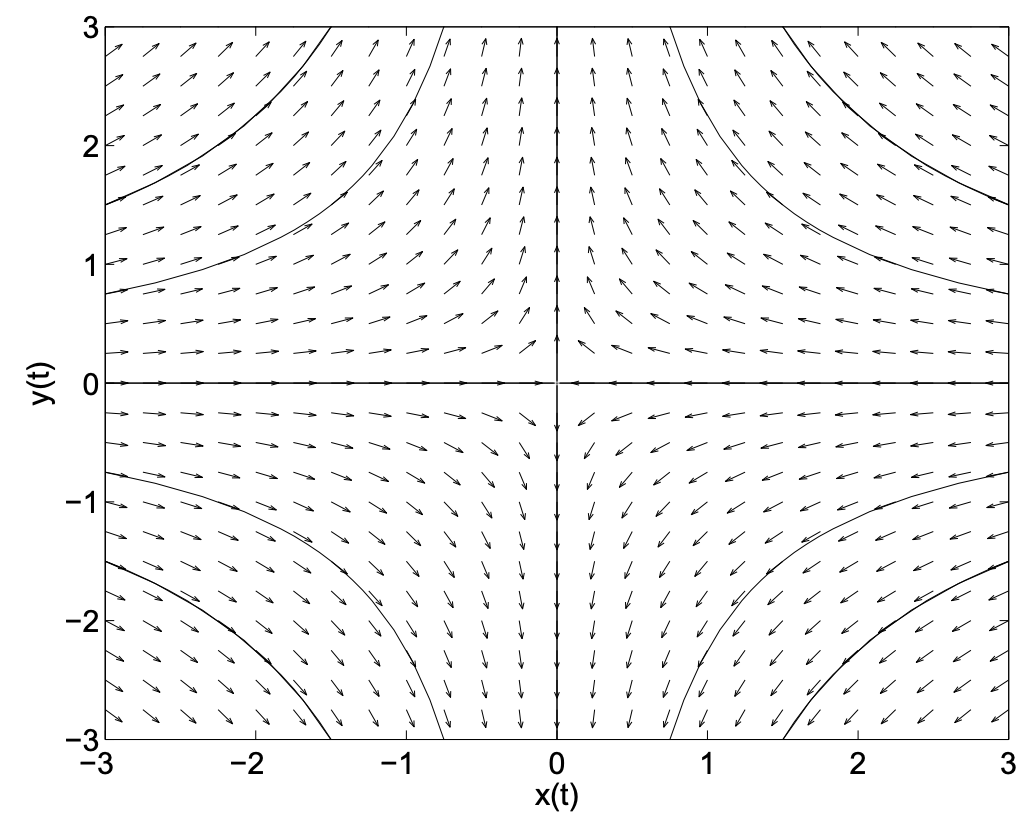
Similar al primer ejemplo, podemos observar una variedad de parcelas. Estos están dados por las Figuras 2.6-2.7. Las órbitas se pueden obtener del sistema como
\[\dfrac{d y}{d x}=\dfrac{d y / d t}{d x / d t}=-\dfrac{y}{x} \nonumber \]
La solución es\(y=\dfrac{A}{x}\). Para diferentes valores de\(A \neq 0\) obtenemos una familia de hipérbolas. Estas son las mismas curvas que se podrían obtener para las curvas de nivel de una superficie conocida como superficie de sillín,\(z=x y\). Así, este tipo de punto de equilibrio se clasifica como un punto de sillín. A partir del retrato de fase podemos verificar que hay muchas órbitas que alejan del origen (punto de equilibrio), pero hay una línea de condiciones iniciales que conduce al origen y que es el\(x\) eje -eje. En este caso, la línea de condiciones iniciales viene dada por el\(x\) eje -.
\ [\ begin {alineado}
x' &= 2x\\
y' &= y
\ end {alineado}\ etiqueta {2.20}\]
Este ejemplo es similar al Ejemplo 2.3. Las soluciones se obtienen reemplazando\(t\) con\(−t\). Las soluciones, órbitas y campos de dirección se pueden ver en las Figuras 2.8-2.9. Esto vuelve a ser un nodo, pero todas las órbitas se alejan del punto de equilibrio. Se llama nodo inestable o fuente.
Centro
\ [\ begin {alineado}
x' &= y\\
y' &= -x
\ end {alineado}\ etiqueta {2.21}\]
Este sistema es un sistema simple, acoplado. Ninguna ecuación puede resolverse sin alguna información sobre la otra función desconocida. Sin embargo, podemos diferenciar la primera ecuación y usar la segunda ecuación para obtener
\[x'' + x = 0. \nonumber \]
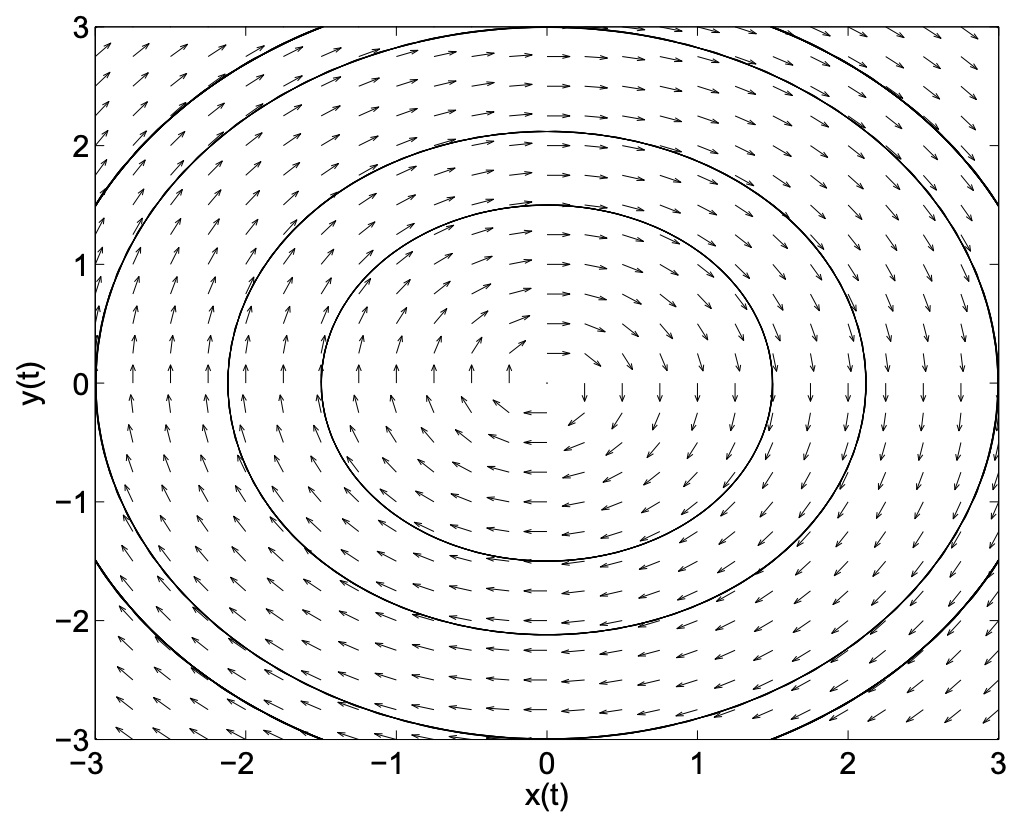
Reconocemos esta ecuación del último capítulo como aquella que aparece en el estudio del movimiento armónico simple. Las soluciones son oscilaciones sinusoidales puras:
\[x(t) = c_1 \cos t + c_2 \sin t, \quad y(t) = -c_1 \sin t + c_2 \cos t. \nonumber \]
En el plano de fase, las trayectorias se pueden determinar mirando el campo de dirección o resolviendo la ecuación de primer orden
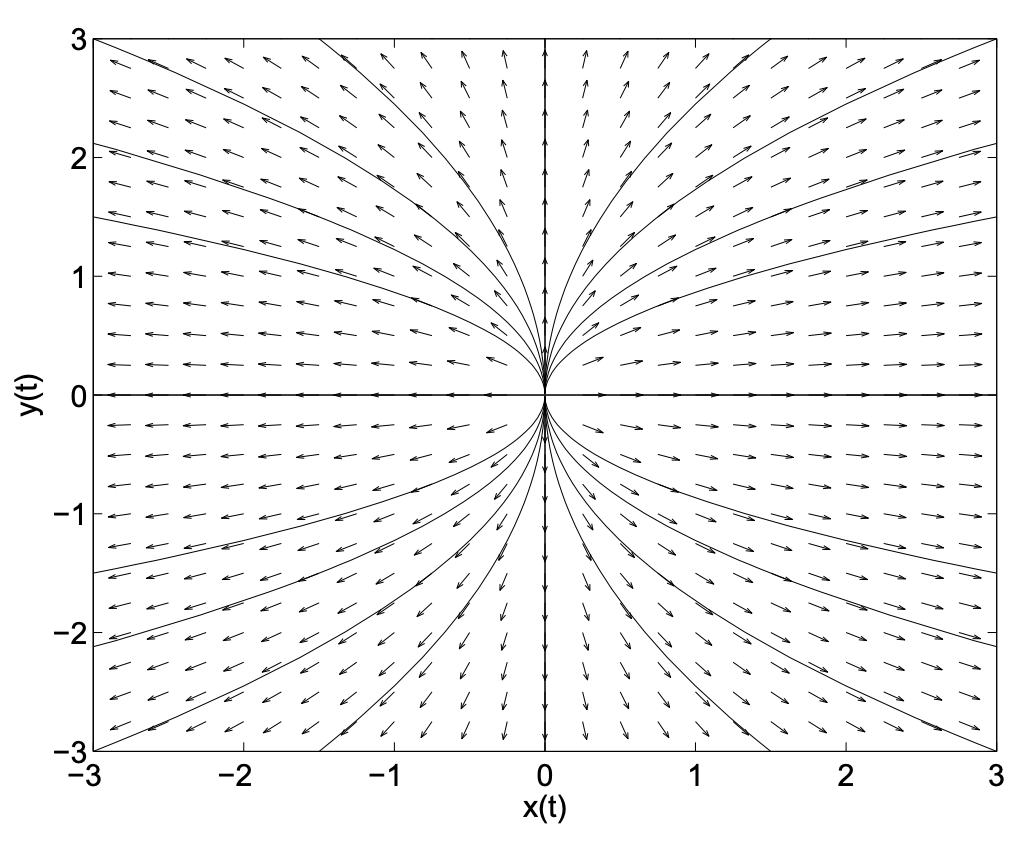
\[\dfrac{d y}{d x}=-\dfrac{x}{y} \nonumber \]
Realizando una separación de variables e integrando, encontramos que
\[x^{2}+y^{2}=C \nonumber \]
Así, tenemos una familia de círculos para\(C>0\). (¿Puedes probarlo usando la solución general?) Al observar los resultados gráficamente en las Figuras 2.10-2.11, se confirma este resultado. Este tipo de punto se llama centro.
\ [\ begin {aligned}
&x^ {\ prime} =\ alpha x+y\\
&y^ {\ prime} =-x
\ end {alineado}\ label {2.22}\]
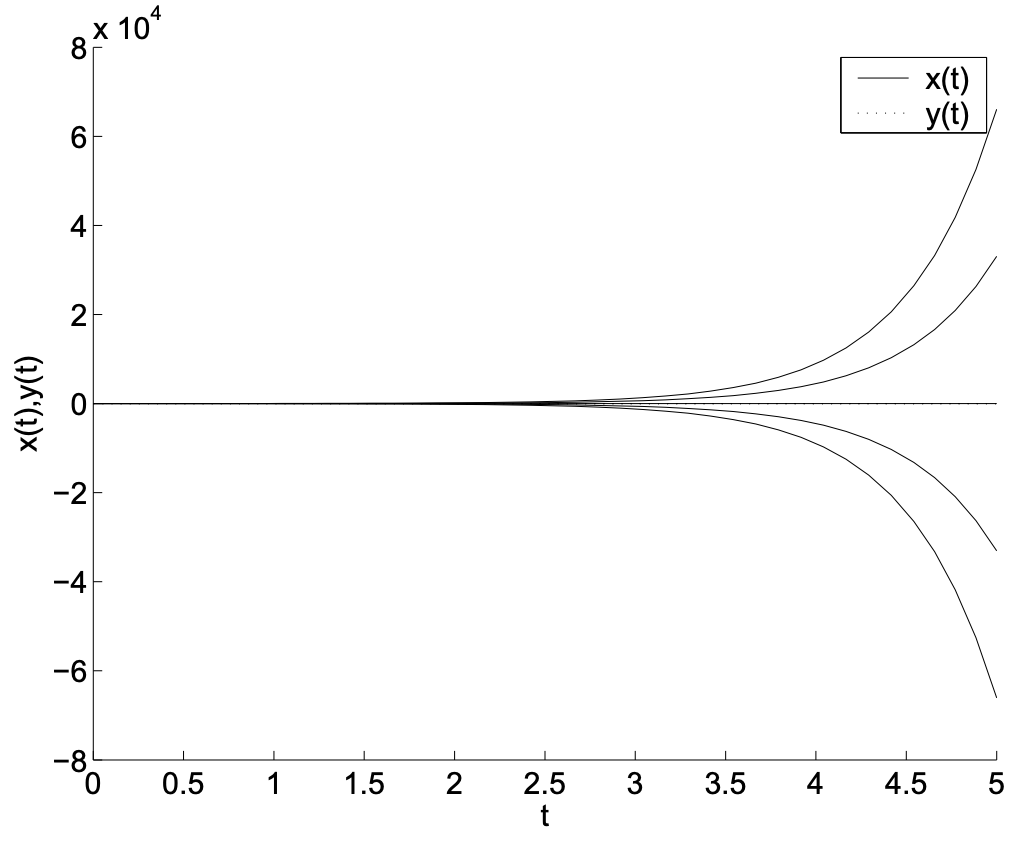
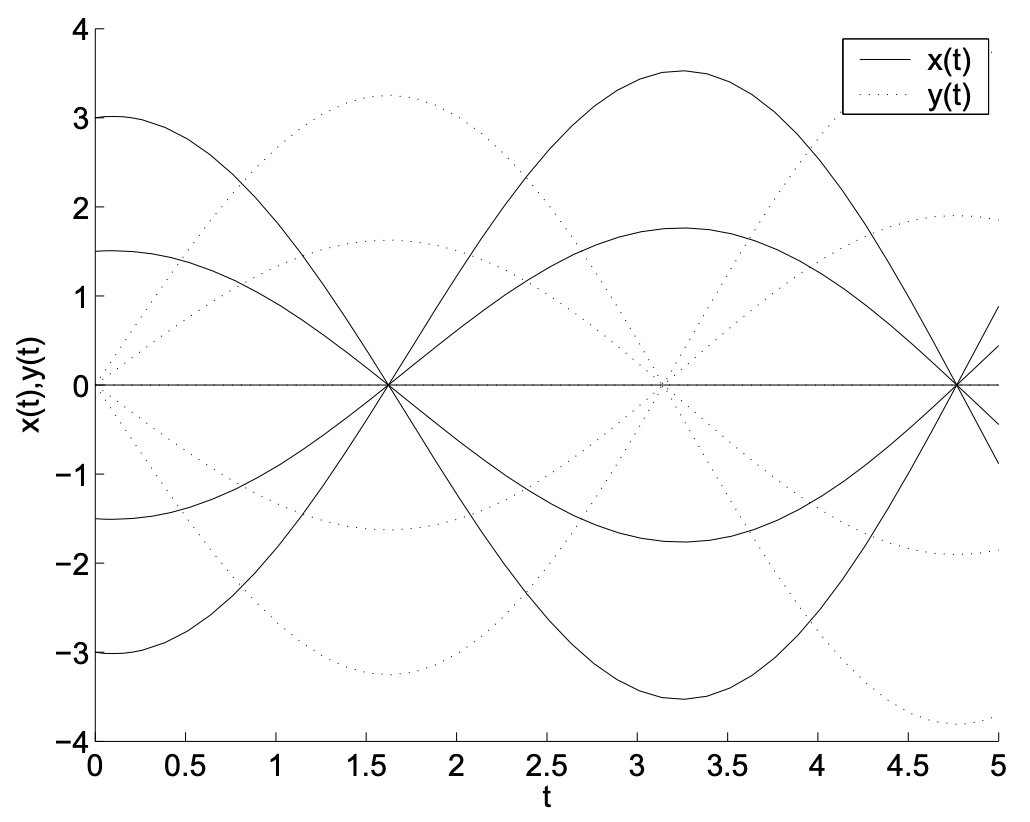
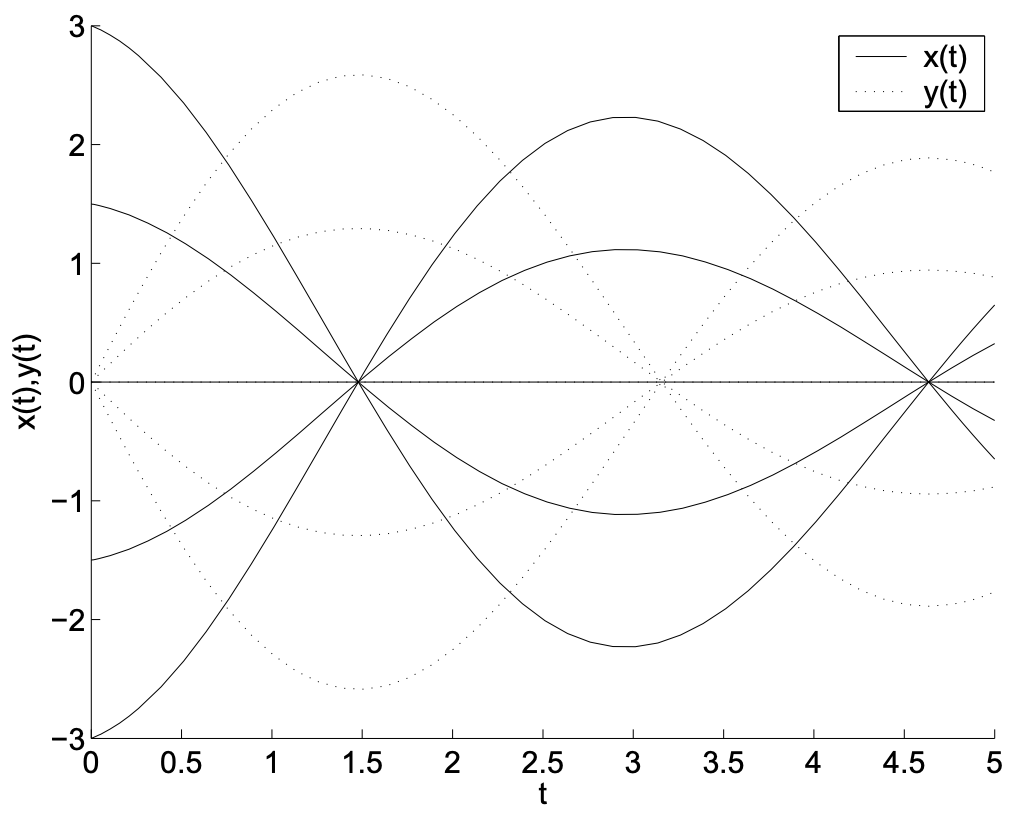
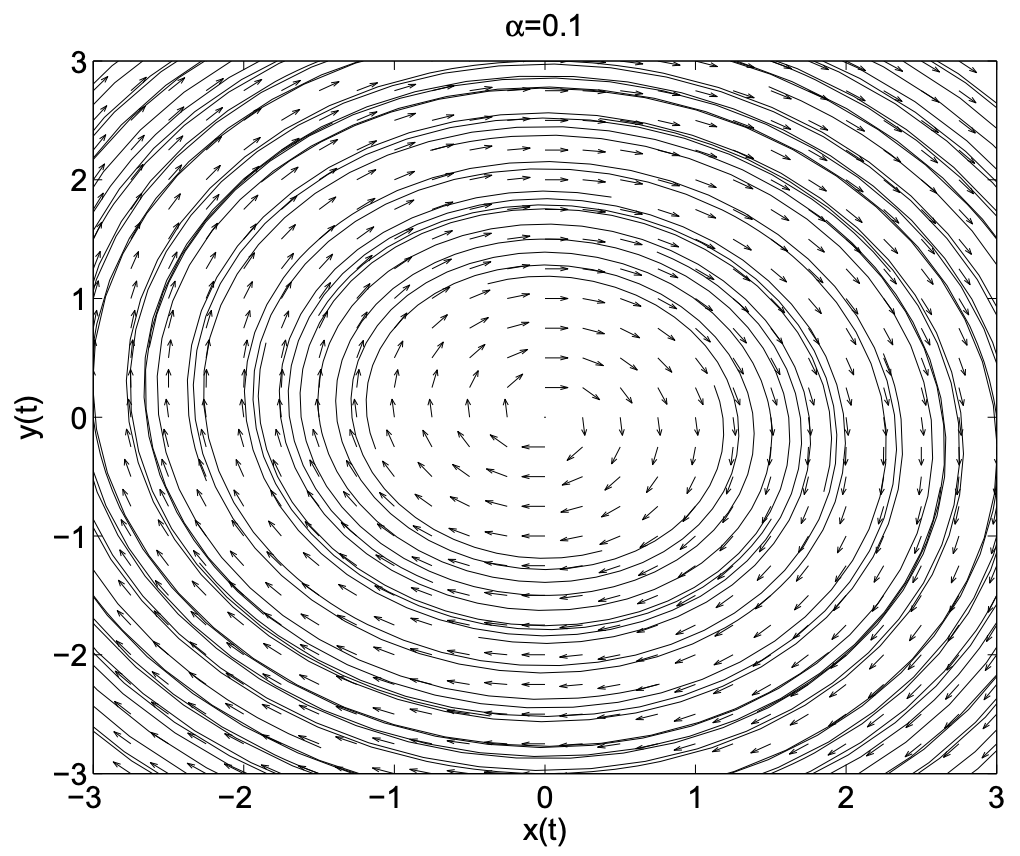
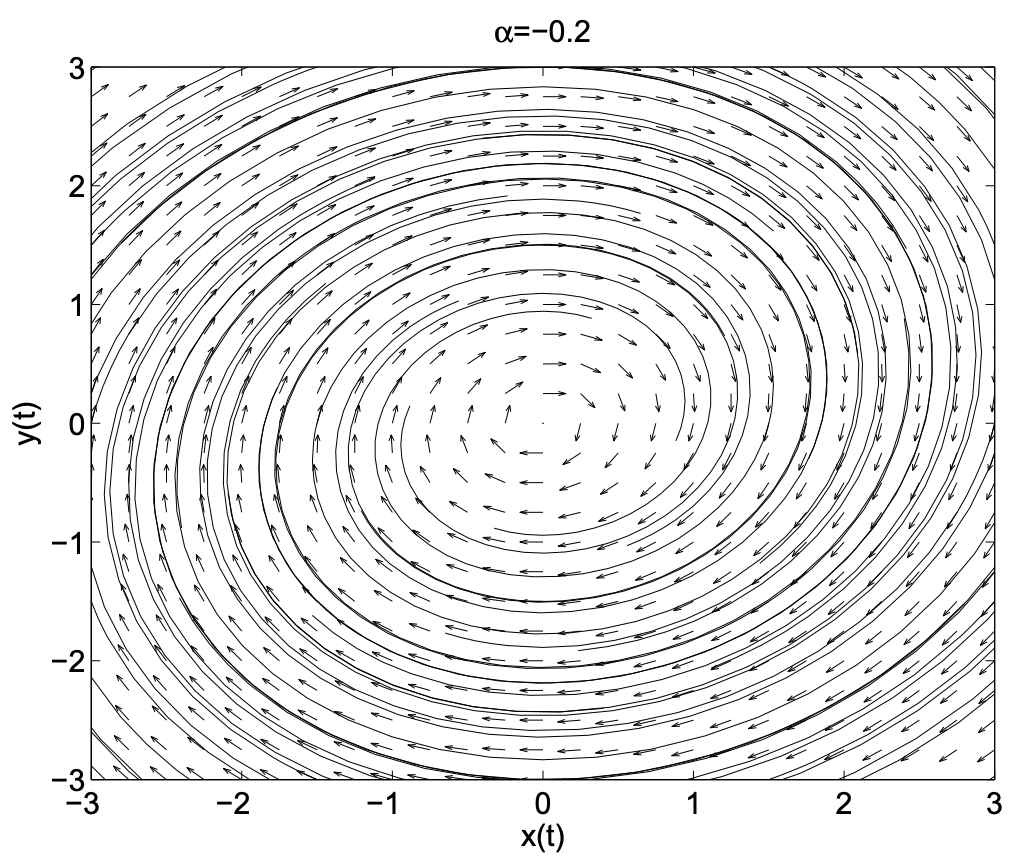
En este ejemplo, veremos un conjunto adicional de comportamientos de puntos de equilibrio en sistemas planos. Hemos agregado un término,\(\alpha x\), al sistema en el Ejemplo 2.7. Consideraremos los efectos para dos valores específicos del parámetro:\(\alpha=0.1,-0.2\). Los comportamientos resultantes se muestran en las gráficas restantes. Vemos órbitas que parecen espirales. Estas órbitas son espirales estables e inestables (o focos, el plural de foco).
Podemos entender estos comportamientos relacionando una vez más el sistema de ecuaciones diferenciales de primer orden con una ecuación diferencial de segundo orden. Usando nuestro método habitual para obtener una ecuación de segundo orden de un sistema, encontramos que\(x(t)\) satisface la ecuación diferencial
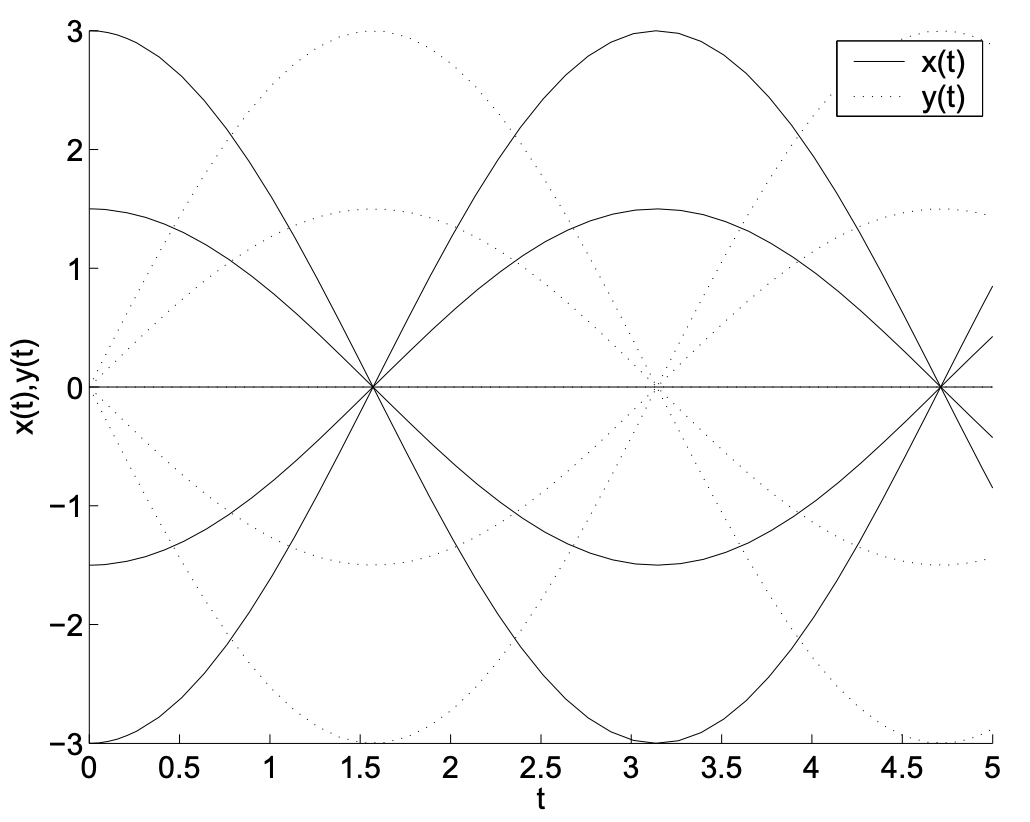
\[x'' - \alpha x' + x = 0. \nonumber \]
Recordamos de nuestro primer curso que esta es una forma de movimiento armónico simple amortiguado. Exploraremos los diferentes tipos de soluciones que resultarán para\(\alpha\) varios's.
La ecuación característica es\(r^2 - \alpha r + 1 = 0\). La solución de esta ecuación cuadrática es
\[r = \dfrac{\alpha \pm \sqrt{\alpha^2 - 4}{2}. \nonumber \]
Hay cinco casos especiales a considerar como se muestra a continuación.
- \(\alpha=-2\). Hay una solución real. A este caso se le llama amortiguación crítica ya que la solución\(r=-1\) conduce a un decaimiento exponencial. La solución es\(x(t)=\left(c_{1}+c_{2} t\right) e^{-t}\).
- \(\alpha<-2\). Hay dos soluciones reales, negativas,\(r=-\mu,-\nu\),\(\mu, \nu>0\). La solución es\(x(t)=c_{1} e^{-\mu t}+c_{2} e^{-\nu t}\). En este caso tenemos lo que se llama movimiento sobreamortiguado. No hay oscilaciones
- \(-2<\alpha<0\). Hay dos soluciones conjugadas complejas\(r= \alpha / 2 \pm i \beta\) con parte real menor a cero y\(\beta=\dfrac{\sqrt{4-\alpha^{2}}}{2}\). La solución es\(x(t)=\left(c_{1} \cos \beta t+c_{2} \sin \beta t\right) e^{\alpha t / 2}\). Ya que\(\alpha<0\), esto consiste en unas oscilaciones de tiempos exponenciales en descomposición. Esto a menudo se llama una oscilación subamortiguada.
- \(\alpha=0\). Esto conduce a un simple movimiento armónico.
- \(0<\alpha<2\). Esto es similar al caso subamortiguado, excepto\(\alpha>0\). Las soluciones son oscilaciones crecientes.
- \(\alpha=2\). Hay una solución real. La solución es\(x(t)=\left(c_{1}+\right.\)\(\left.c_{2} t\right) e^{t}\). Conduce a un crecimiento sin límites en el tiempo.
- Para\(\alpha>2\). Hay dos soluciones reales y positivas\(r=\mu, \nu>0\). La solución es\(x(t)=c_{1} e^{\mu t}+c_{2} e^{\nu t}\), que crece en el tiempo.
Para\(\alpha<0\) las soluciones están perdiendo energía, por lo que las soluciones pueden oscilar con una amplitud decreciente. Porque\(\alpha>0\), hay un crecimiento en la amplitud, lo cual no es típico. Por supuesto, puede haber un movimiento sobreamortiguado si la magnitud de\(\alpha\) es demasiado grande.
\ [\ begin {aligned}
&x^ {\ prime} =-x\\
&y^ {\ prime} =-2 x-y
\ end {alineado}\ etiqueta {2.23}\]
Para este ejemplo, escribimos las soluciones. Si bien es un sistema acoplado, solo se acopla la segunda ecuación. Hay dos enfoques posibles.
a. Podríamos resolver la primera ecuación a encontrar\(x(t)=c_{1} e^{-t}\). Insertando esta solución en la segunda ecuación, tenemos
\(y^{\prime}+y=-2 c_{1} e^{-t}\)
Esta es una ecuación lineal de primer orden relativamente simple para\(y=y(t)\). El factor integrador es\(\mu=e^{t}\). La solución se encuentra como\(y(t)=\left(c_{2}-2 c_{1} t\right) e^{-t}\).
b. Otro método sería proceder a reescribir esto como una ecuación de segundo orden. \(x^{\prime \prime}\)La computación no nos lleva muy lejos. Entonces, miramos
\ [\ begin {alineado}
y^ {\ prime\ prime} &=-2 x^ {\ prime} -y^ {\ prime}\\
&=2 x-y^ {\ prime}\\
&=-2 y^ {\ prime} -y
\ end {alineado}\ etiqueta {2.24}\]
Por lo tanto,\(y\) satisface
\[y^{\prime \prime}+2 y^{\prime}+y=0 \nonumber \]
La ecuación característica tiene una raíz real,\(r=-1\). Entonces, escribimos
\[y(t)=\left(k_{1}+k_{2} t\right) e^{-t} \nonumber \]
Este es un nodo degenerado estable. Combinando esto con la solución\(x(t)= c_{1} e^{-t}\), podemos demostrarlo\(y(t)=\left(c_{2}-2 c_{1} t\right) e^{-t}\) como antes.
En la Figura 2.16 vemos varias órbitas en este sistema. Se diferencia del nodo estable que se muestra en la Figura 2.2 en que solo hay una dirección a lo largo de la cual las órbitas se acercan al origen en lugar de dos. Si uno elige\(c_{1}=0\), entonces\(x(t)=0\) y\(y(t)=c_{2} e^{-t}\). Esto conduce a órbitas que discurren a lo largo del\(y\) eje como se ve en la figura.
\ [\ begin {aligned}
&x^ {\ prime} =2 x-y\\
&y^ {\ prime} =-2 x+y
\ end {alineado}\ label {2.25}\]
En este último ejemplo, tenemos un conjunto acoplado de ecuaciones. Lo reescribimos como una ecuación diferencial de segundo orden:
\ [\ begin {alineado}
x^ {\ prime\ prime} &=2 x^ {\ prime} -y^ {\ prime}\\
&=2 x^ {\ prime} - (-2 x+y)\\
&=2 x^ {\ prime} +2 x+\ izquierda (x^ {\ prime} -2 x\ derecha) =3 x^ {\ prime}
\ end {alineado}\ etiqueta {26}\]
Entonces, la ecuación de segundo orden es
\[x^{\prime \prime}-3 x^{\prime}=0 \nonumber \]
y la ecuación característica es\(0=r(r-3)\). Esto da la solución general como
\[x(t)=c_{1}+c_{2} e^{3} t \nonumber \]
y por lo tanto
\[y=2 x-x^{\prime}=2\left(c_{1}+c_{2}^{3} t\right)-\left(3 c_{2} e^{3 t}\right)=2 c_{1}-c_{2} e^{3 t} \nonumber \]
En la Figura 2.17 mostramos el campo de dirección. El campo de pendiente constante que se ve en este ejemplo se confirma mediante un simple cálculo:
\[\dfrac{d y}{d x}=\dfrac{-2 x+y}{2 x-y}=-1 \nonumber \]
Además, mirando las condiciones iniciales con\(y=2 x\), tenemos en\(t=0\),
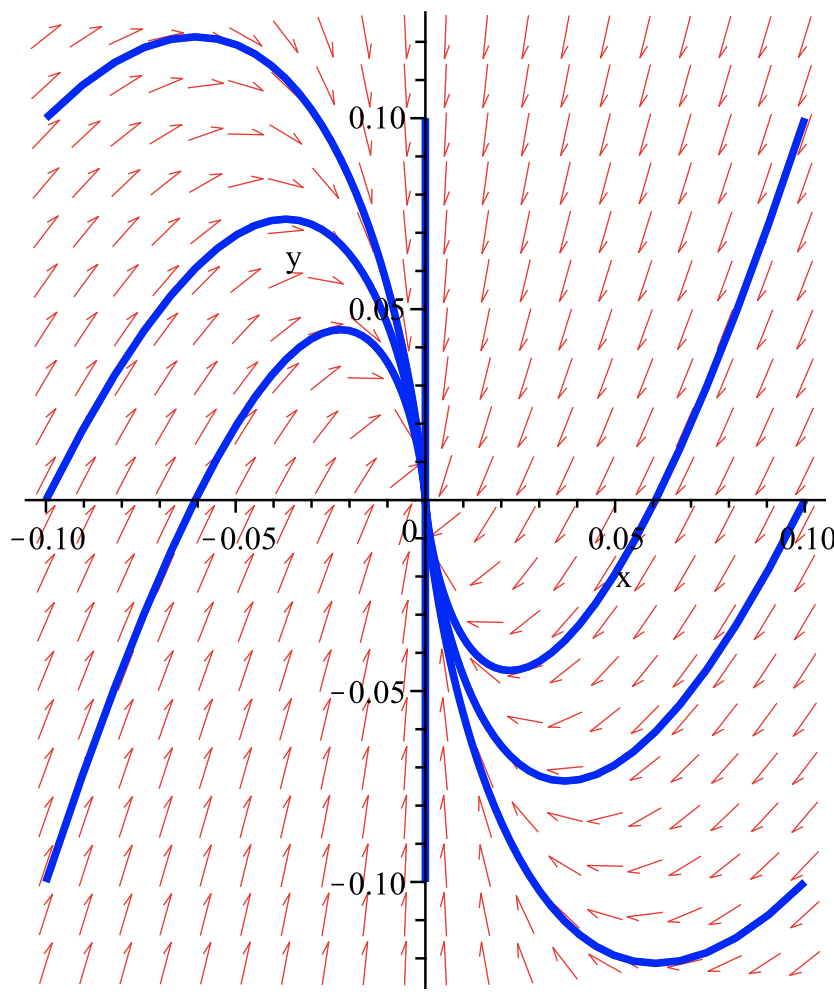
\[2 c_{1}-c_{2}=2\left(c_{1}+c_{2}\right) \quad \Rightarrow \quad c_{2}=0 \nonumber \]
Por lo tanto, los puntos en esta línea permanecen en esta línea para siempre,\((x, y)=\left(c_{1}, 2 c_{1}\right)\). Esta línea de puntos fijos se denomina línea de equilibrios.
2.2.1 Representación Polar de Espirales
En los ejemplos con un centro o una espiral, uno podría ser capaz de escribir las soluciones en coordenadas polares. Recordemos que un punto en el plano puede ser descrito por\((r, \theta)\) coordenadas cartesianas\((x, y)\) o polares. Dada la forma polar, se pueden encontrar los componentes cartesianos usando
\[x=r \cos \theta \text { and } y=r \sin \theta \nonumber \]
Dadas las coordenadas cartesianas, se pueden encontrar las coordenadas polares usando
\[r^{2}=x^{2}+y^{2} \text { and } \tan \theta=\dfrac{y}{x} \label{2.27} \]
Ya que\(x\) y\(y\) son funciones de\(t\), entonces naturalmente podemos pensar en\(r\) y\(\theta\) como funciones de\(t\). Las ecuaciones que satisfacen se obtienen diferenciando las relaciones anteriores con respecto a\(t\).
Diferenciar la primera ecuación en (2.27) da
\[r r^{\prime}=x x^{\prime}+y y^{\prime}. \nonumber \]
Insertando las expresiones para\(x^{\prime}\) y\(y^{\prime}\) desde el sistema 2.5, tenemos
\[r r^{\prime}=x(a x+b y)+y(c x+d y) \nonumber \]
En algunos casos esto puede estar escrito enteramente en términos de\(r\)'s. Del mismo modo, tenemos que
\[\theta^{\prime}=\dfrac{x y^{\prime}-y x^{\prime}}{r^{2}} \nonumber \]
que el lector puede probar para la tarea.
En resumen, al convertir ecuaciones de primer orden de forma rectangular a polar, se necesitan las siguientes relaciones.
\ [\ begin {alineado}
r^ {\ prime} &=\ dfrac {x x^ {\ prime} +y y^ {\ prime}} {r}\\
\ theta^ {\ prime} &=\ dfrac {x y^ {\ prime} -y x^ {\ prime}} {r^ {2}}
\ end {alineado}\ etiqueta {2.28}\]
\ [\ begin {alineado}
&x^ {\ prime} =a x+b y\\
&y^ {\ prime} =-b x+a y
\ end {alineado}\ etiqueta {2.29}\]
Primero calculamos\(r^{\prime}\) y\(\theta^{\prime}\):
\ begin {alineado}
r r^ {\ prime} &=x x^ {\ prime} +y y^ {\ prime} =x (a x+b y) +y (-b x+a y) =a r^ {2}\\
r^ {2}\ theta^ {\ prime} &=x y^ {\ prime} -y x^ {\ prime} =x (-b +a y) -y (a x+b y) =-b r^ {2}
\ final {alineado}
Esto lleva a un sistema más simple
\ [\ begin {aligned}
&r^ {\ prime} =a r\\
&\ theta^ {\ prime} =-b
\ end {alineado}\ label {2.30}\]
Este sistema está desacoplado. La segunda ecuación en este sistema indica que atravesamos la órbita a una velocidad constante en el sentido de las agujas del reloj. Resolviendo estas ecuaciones, tenemos eso\(r(t)=r_{0} e^{a t}, \quad \theta(t)=\theta_{0}-b t\). Eliminando\(t\) entre estas soluciones, finalmente encontramos la ecuación polar de las órbitas:
\[r=r_{0} e^{-a\left(\theta-\theta_{0}\right) t / b} \nonumber \]
Si graficas esto para\(a \neq 0\), obtendrás espirales estables o inestables.
\ [\ begin {aligned}
&x^ {\ prime} =-y+x\\
&y^ {\ prime} =x+y
\ end {alineado}\ label {2.31}\]
Para convertir este sistema en forma polar, calculamos
\ begin {reunió}
r r^ {\ prime} =x x^ {\ prime} +y y^ {\ prime} =x (-y+x) +y (x+y) =r^ {2}\
r^ {2}\ theta^ {\ prime} =x y^ {\ prime} -y x^ {\ prime} =x (x+y) -y (-y+x) =r^ {2}
\ fin {reunidos}
Esto lleva a un sistema más simple
\ [\ begin {aligned}
&r^ {\ prime} =r\\
&\ theta^ {\ prime} =1
\ end {alineado}\ label {2.32}\]
Resolver estas ecuaciones rinde
\[r(t)=r_{0} e^{t}, \quad \theta(t)=t+\theta_{0} \nonumber \]
La eliminación\(t\) de esta solución da las órbitas en el plano de fase,\(r(\theta)=\)\(r_{0} e^{\theta-\theta_{0}}\)
Un ejemplo más complicado surge para un sistema no lineal de ecuaciones diferenciales. Considera el siguiente ejemplo.
\ [\ begin {aligned}
&x^ {\ prime} =-y+x\ izquierda (1-x^ {2} -y^ {2}\ derecha)\\
&y^ {\ prime} =x+y\ izquierda (1-x^ {2} -y^ {2}\ derecha)
\ end {alineado}\ label {2.33}\]
Transformándose a coordenadas polares, se puede demostrar que Para convertir este sistema en forma polar, calculamos
\[r^{\prime}=r\left(1-r^{2}\right), \quad \theta^{\prime}=1 \nonumber \]
Este sistema desacoplado se puede resolver y dichos sistemas no lineales se estudiarán en el siguiente capítulo.


