5.3: Serie de Fourier a lo largo de otros intervalos
- Page ID
- 118976
En muchas aplicaciones estamos interesados en determinar representaciones en series de Fourier de funciones definidas en intervalos distintos a\([0,2 \pi]\). En esta sección determinaremos la forma de la expansión en serie y los coeficientes de Fourier en estos casos.
El tipo de intervalo más general se da como\([a, b]\). Sin embargo, esto a menudo es demasiado general. Los intervalos más comunes son de la forma\([-\pi, \pi],[0, L]\), o\([-L / 2, L / 2]\). La generalización más simple es al intervalo\([0, L]\). Tales intervalos surgen a menudo en aplicaciones. Por ejemplo, se pueden estudiar las vibraciones de una cuerda unidimensional de longitud\(L\) y configurar los ejes con el extremo izquierdo en\(x=0\) y el extremo derecho en\(x=L\). Otro problema sería estudiar la distribución de temperatura a lo largo de una varilla unidimensional de longitud\(L\). Tales problemas conducen a los estudios originales de las series de Fourier. Como veremos más adelante, los intervalos simétricos,\([-a, a]\), también son útiles.
Dado un intervalo\([0, L]\), podríamos aplicar una transformación a un intervalo de longitud\(2 \pi\) simplemente reescalando nuestro intervalo. Entonces podríamos aplicar esta transformación a nuestra representación en serie de Fourier para obtener una equivalente útil para las funciones definidas en\([0, L]\).
Definimos\(x \in[0,2 \pi]\) y\(t \in[0, L]\). Una transformación lineal que relaciona estos intervalos es simplemente\(x=\dfrac{2 \pi t}{L}\) como se muestra en la Figura 5.5. Entonces,\(t=0\) mapas a\(x=0\) y\(t=L\) mapas a\(x=2 \pi\). Además, esta transformación se mapea\(f(x)\) a una nueva función\(g(t)=f(x(t))\), que se define en\([0, L]\). Determinaremos la representación en serie de Fourier de esta función usando la representación para\(f(x)\).
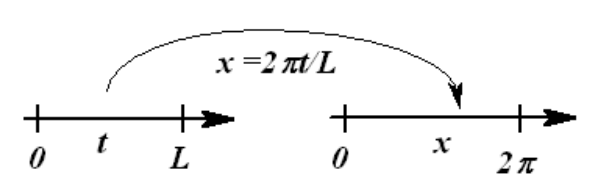
Recordemos la forma de la representación de Fourier para\(f(x)\) en la Ecuación (5.1):
\[f(x) \sim \dfrac{a_{0}}{2}+\sum_{n=1}^{\infty}\left[a_{n} \cos n x+b_{n} \sin n x\right] . \label{5.23} \]
Insertando la transformación relativa\(x\) y\(t\), tenemos
\[g(t) \sim \dfrac{a_{0}}{2}+\sum_{n=1}^{\infty}\left[a_{n} \cos \dfrac{2 n \pi t}{L}+b_{n} \sin \dfrac{2 n \pi t}{L}\right] . \label{5.24} \]
Esto da la forma de la expansión en serie para\(g(t)\) con\(t \in[0, L]\). Pero, aún necesitamos determinar los coeficientes de Fourier.
Recordemos, que
\[a_{n}=\dfrac{1}{\pi} \int_{0}^{2 \pi} f(x) \cos n x d x \nonumber \]
Tenemos que hacer una sustitución en la integral de\(x=\dfrac{2 \pi t}{L}\). También habrá que transformar el diferencial,\(d x=\dfrac{2 \pi}{L} d t\). Así, la forma resultante para nuestro coeficiente es
\[a_{n}=\dfrac{2}{L} \int_{0}^{L} g(t) \cos \dfrac{2 n \pi t}{L} d t \label{5.25} \]
Del mismo modo, encontramos que
\[b_{n}=\dfrac{2}{L} \int_{0}^{L} g(t) \sin \dfrac{2 n \pi t}{L} d t \label{5.26} \]
Notamos primero que cuando\(L=2 \pi\) volvemos la representación de la serie que estudiamos por primera vez. También, el periodo de\(\cos \dfrac{2 n \pi t}{L}\) es\(L / n\), lo que significa que la representación para\(g(t)\) tiene un periodo de\(L\).
Al final de esta sección se presenta la derivación de la representación de la serie de Fourier para un intervalo general para el lector interesado. En el Cuadro 5.1 resumimos algunas representaciones de series de Fourier de uso común.
Terminaremos nuestra discusión por ahora con algunos casos especiales y un ejemplo para una función definida en\([-\pi, \pi]\).
Ejemplo 5.7. \(f(x)=|x|\)Vamos\([-\pi, \pi]\) Calculamos los coeficientes, comenzando como de costumbre con\(a_{0}\). Tenemos
\ [\ begin {alineado}
a_ {0} &=\ dfrac {1} {\ pi}\ int_ {-\ pi} ^ {\ pi} |x| d x\\
&=\ dfrac {2} {\ pi}\ int_ {0} ^ {\ pi} |x| d x=\ pi
\ final {alineado}\ etiqueta {5.33}\]
En este punto hay que recordar al lector sobre la integración de funciones pares e impares.
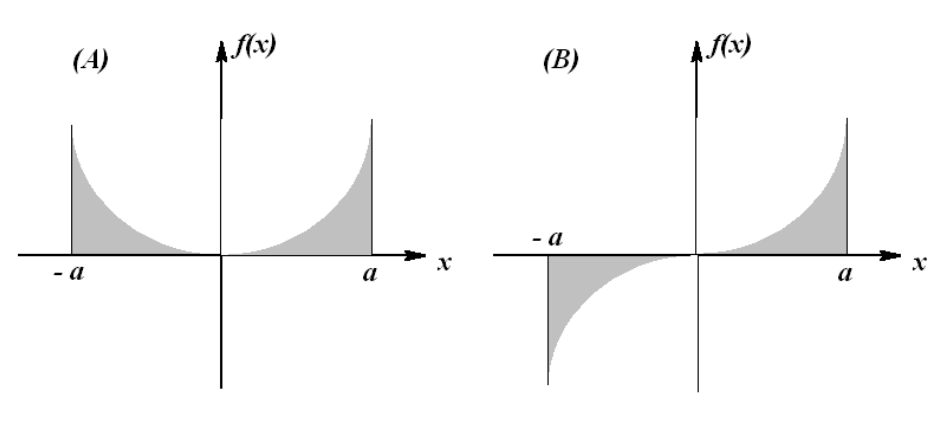
1. Incluso Funciones: En esta evaluación hicimos uso del hecho de que el integrando es una función par. Recordemos que\(f(x)\) es una función par si es\(f(-x)=f(x)\) para todos\(x\). Se pueden reconocer funciones pares ya que son simétricas con respecto al\(y\) eje -como se muestra en la Figura 5.6 (A). Si uno integra una función par a lo largo de un intervalo simétrico, entonces uno tiene esa
\[\int_{-a}^{a} f(x) d x=2 \int_{0}^{a} f(x) d x \label{5.34} \]
Se puede probar esto dividiendo la integración sobre valores negativos de\(x\), usando la sustitución\(x=-y\), y empleando la uniformidad de\(f(x)\). Por lo tanto,
|
Serie de Fourier en\([0, L]\) \[f(x) \sim \dfrac{a_{0}}{2}+\sum_{n=1}^{\infty}\left[a_{n} \cos \dfrac{2 n \pi x}{L}+b_{n} \sin \dfrac{2 n \pi x}{L}\right] \label{5.27} \] \ [\ begin {alineado} |
|
Serie de Fourier en\(\left[-\dfrac{L}{2}, \dfrac{L}{2}\right]\) \[f(x) \sim \dfrac{a_{0}}{2}+\sum_{n=1}^{\infty}\left[a_{n} \cos \dfrac{2 n \pi x}{L}+b_{n} \sin \dfrac{2 n \pi x}{L}\right] \label{5.29} \] \ [\ begin {alineado} |
|
Serie de Fourier en\([-\pi, \pi]\) \[f(x) \sim \dfrac{a_{0}}{2}+\sum_{n=1}^{\infty}\left[a_{n} \cos n x+b_{n} \sin n x\right] \label{5.31} \] \ [\ comenzar {reunido} |
Cuadro 5.1. Representaciones especiales de series de Fourier en diferentes intervalos
\ [\ begin {alineado}
\ int_ {-a} ^ {a} f (x) d x &=\ int_ {-a} ^ {0} f (x) d x+\ int_ {0} ^ {a} f (x) d x\\
&=-\ int_ {a} ^ {0} f (-y) d y+\ int_ {0} ^ {a} f (x) d x\\
&=\ int_ {0} ^ {a} f (y) d y+\ int_ {0} ^ {a} f (x) d x\\
&=2\ int_ {0} ^ {a} f (x) d x
\ end { alineado}\ etiqueta {5.35}\]
Esto se puede verificar visualmente mirando Figura\(5.6(\mathrm{~A})\).
2. Funciones impares: Se podría hacer un cálculo similar para funciones impares. \(f(x)\)es una función impar si es\(f(-x)=-f(x)\) para todos\(x\). Las gráficas de tales funciones son simétricas con respecto al origen como se muestra en la Figura\(5.6(\mathrm{~B})\). Si uno integra una función impar sobre un intervalo simétrico, entonces uno tiene esa
\[\int_{-a}^{a} f(x) d x=0 \label{5.36} \]
Ahora continuamos con nuestro cálculo de los coeficientes de Fourier para\(f(x)=|x|\) on\([-\pi, \pi]\). Tenemos
\[a_{n}=\dfrac{1}{\pi} \int_{-\pi}^{\pi}|x| \cos n x d x=\dfrac{2}{\pi} \int_{0}^{\pi} x \cos n x d x \label{5.37} \]
Aquí hemos hecho uso del hecho de que\(|x| \cos n x\) es una función par. Para poder calcular la integral resultante, necesitamos utilizar la integración por partes,
\[\int_{a}^{b} u d v=\left.u v\right|_{a} ^{b}-\int_{a}^{b} v d u \nonumber \]
por dejar\(u=x\) y\(d v=\cos n x d x\). Así,\(d u=d x\) y\(v=\int d v=\dfrac{1}{n} \sin n x\).
Continuando con el cómputo, tenemos
\ [\ begin {alineado}
a_ {n} &=\ dfrac {2} {\ pi}\ int_ {0} ^ {\ pi} x\ cos n x d x\\
&=\ dfrac {2} {\ pi}\ left [\ left. \ dfrac {1} {n} x\ sin n x\ derecha|_ {0} ^ {\ pi} -\ dfrac {1} {n}\ int_ {0} ^ {\ pi}\ sin n x d x\ derecha]\\
&=-\ dfrac {2} {n\ pi}\ izquierda [-\ dfrac {1} {n}\ cos x\ derecha] _ {0} ^ {\ pi}\\
&=-\ dfrac {2} {\ pi n^ {2}}\ izquierda (1- (-1) ^ {n}\ derecha)
\ final {alineado}\ etiqueta {5.38}\]
Aquí hemos utilizado el hecho de que\(\cos n \pi=(-1)^{n}\) para cualquier entero\(n\). Esto lleva a un factor\(\left(1-(-1)^{n}\right)\). Este factor puede simplificarse como
\ [1- (-1) ^ {n} =\ left\ {\ begin {array} {l}
2, n\ text {impar}\\
0, n\ text {par}
\ end {array}. \ derecho. \ label {5.39}\]
Entonces,\(a_{n}=0\) para\(n\) par y\(a_{n}=-\dfrac{4}{\pi n^{2}}\) para\(n\) impar.
Computar los\(b_{n}\)'s es más sencillo. Observamos que tenemos que integrarnos\(|x| \sin n x\) de\(x=-\pi\) a\(\pi\). El integrando es una función impar y este es un intervalo simétrico. Entonces, el resultado es eso\(b_{n}=0\) para todos\(n\).
Armando todo esto, la representación de la serie de Fourier de\(f(x)=|x|\) on\([-\pi, \pi]\) se da como
\[f(x) \sim \dfrac{\pi}{2}-\dfrac{4}{\pi} \sum_{n=1, \text { odd }}^{\infty} \dfrac{\cos n x}{n^{2}} \label{5.40} \]
Si bien esto es correcto, podemos reescribir la suma sobre solo impar\(n\) reindexando. Dejamos\(n=2 k-1\) para\(k=1,2,3, \ldots\). Entonces sólo obtenemos los enteros impares. La serie se puede escribir como
\[f(x) \sim \dfrac{\pi}{2}-\dfrac{4}{\pi} \sum_{k=1}^{\infty} \dfrac{\cos (2 k-1) x}{(2 k-1)^{2}}. \label{5.41} \]
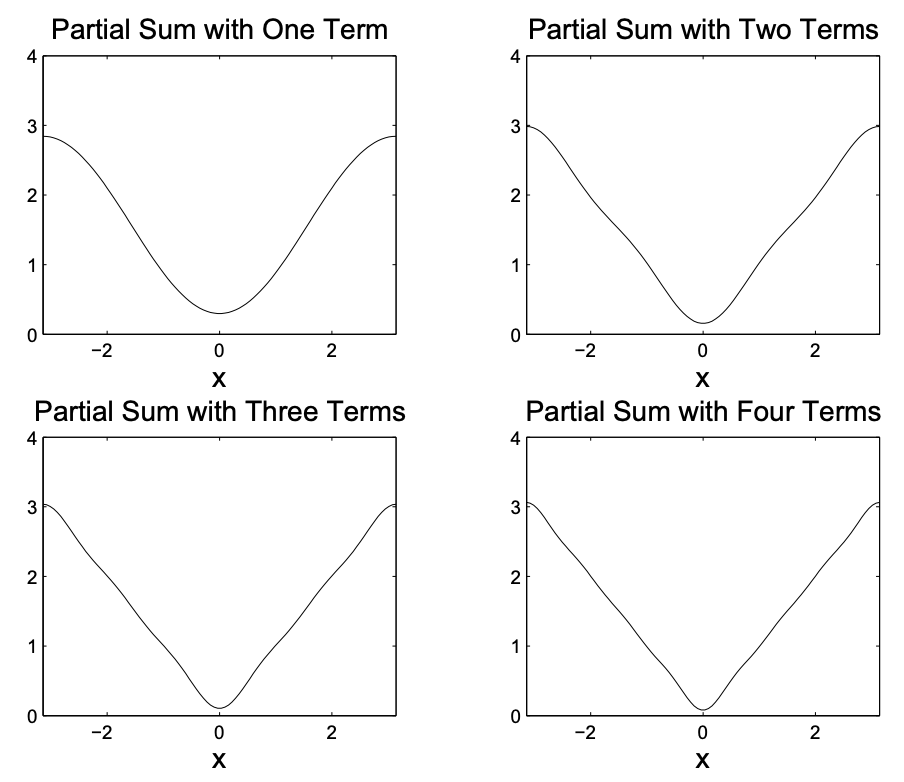
A lo largo de nuestra discusión nos hemos referido a tales resultados como representaciones de Fourier. No hemos mirado la convergencia de estas series. He aquí un ejemplo de una serie infinita de funciones. ¿A qué suma esta serie? Se muestran en la Figura 5.7 las primeras sumas parciales. Parecen estar convergiendo con\(f(x)=|x|\) bastante rapidez.
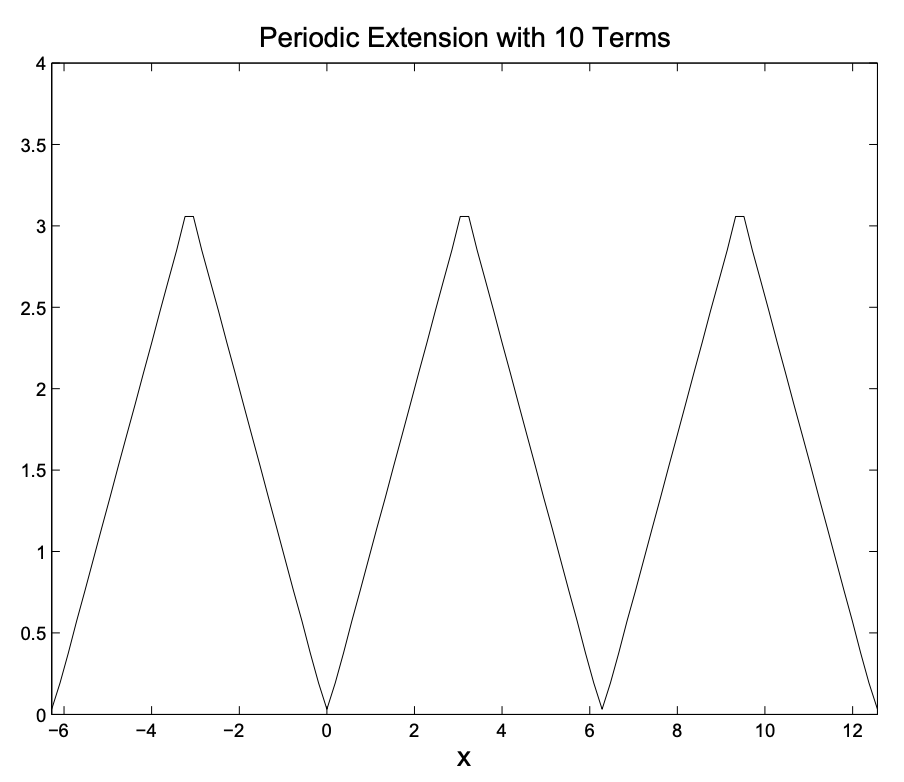
A pesar de que se\(f(x)\) definió en todavía\([-\pi, \pi]\) podemos evaluar la serie de Fourier a valores\(x\) fuera de este intervalo. En la Figura 5.8, vemos que la representación concuerda con\(f(x)\) el intervalo\([-\pi, \pi]\). Fuera de este intervalo tenemos una extensión periódica de\(f(x)\) con periodo\(2 \pi\).
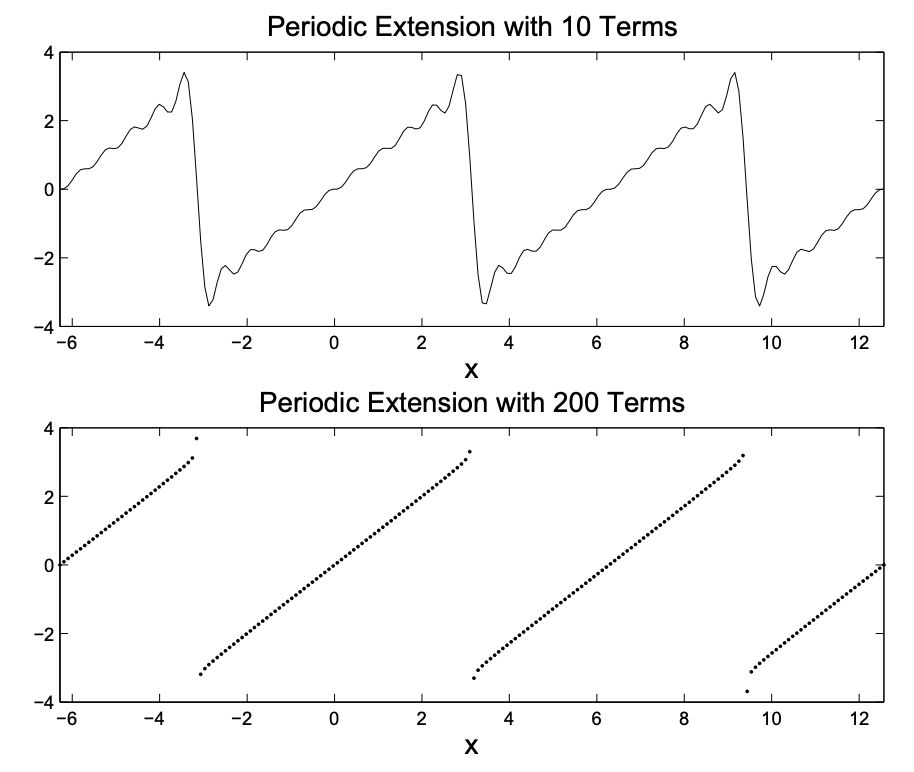
Otro ejemplo es la representación de la serie de Fourier de\(f(x)=x\) on\([-\pi, \pi]\) como izquierda para Problema 5.1. Esto se determina que
\[f(x) \sim 2 \sum_{n=1}^{\infty} \dfrac{(-1)^{n+1}}{n} \sin n x . \label{5.42} \]
Como se ve en la Figura 5.9 obtenemos nuevamente la extensión periódica de nuestra función. En este caso necesitábamos muchos más términos. Además, las partes verticales de la primera parcela son inexistentes. En la segunda gráfica solo trazamos los puntos y no los típicos puntos conectados que la mayoría de los paquetes de software trazan como estilo predeterminado.
Ejemplo 5.8. Es interesante observar que se pueden utilizar series de Fourier para obtener sumas de algunas series infinitas. Por ejemplo, en el último ejemplo encontramos que
\[x \sim 2 \sum_{n=1}^{\infty} \dfrac{(-1)^{n+1}}{n} \sin n x. \nonumber \]
Ahora bien, ¿y si elegimos\(x=\dfrac{\pi}{2}\)? Entonces, tenemos
\[\dfrac{\pi}{2}=2 \sum_{n=1}^{\infty} \dfrac{(-1)^{n+1}}{n} \sin \dfrac{n \pi}{2}=2\left[1-\dfrac{1}{3}+\dfrac{1}{5}-\dfrac{1}{7}+\ldots\right] \nonumber \]
Esto da una expresión bien conocida para\(\pi\):
\[\pi=4\left[1-\dfrac{1}{3}+\dfrac{1}{5}-\dfrac{1}{7}+\ldots\right] \nonumber \]
5.3.1 Serie de Fourier en\([a, b]\)
También es posible una representación en serie de Fourier para un intervalo general,\(t \in[a, b]\). Como antes, solo necesitamos transformar este intervalo en\([0,2 \pi]\). Let
\[x=2 \pi \dfrac{t-a}{b-a}. \nonumber \]
Insertando esto en la representación de la serie de Fourier (5.1)\(f(x)\) para obtener
\[g(t) \sim \dfrac{a_{0}}{2}+\sum_{n=1}^{\infty}\left[a_{n} \cos \dfrac{2 n \pi(t-a)}{b-a}+b_{n} \sin \dfrac{2 n \pi(t-a)}{b-a}\right] \label{5.43} \]
Bueno, esta expansión es fea. No es como el último ejemplo, donde la transformación fue sencilla. Si uno fuera a aplicar la teoría a las aplicaciones, podría parecer que tiene sentido simplemente cambiar los datos para que\(a=0\) y se haga con cualquier expresión complicada. Sin embargo, los estudiantes de matemáticas disfrutan del desafío de desarrollar tales expresiones generalizadas. Entonces, veamos en qué consiste.
Primero, aplicamos las identidades de adición para funciones trigonométricas y reordenamos los términos.
\ [\ begin {alineado}
g (t)\ sim &\ dfrac {a_ {0}} {2} +\ sum_ {n=1} ^ {\ infty}\ left [a_ {n}\ cos\ dfrac {2 n\ pi (t-a)} {b-a} +b_ {n}\ sin\ dfrac {2 n\ pi (t-a)} b-{ a}\ derecha]\\
=&\ dfrac {a_ {0}} {2} +\ sum_ {n=1} ^ {\ infty}\ izquierda [a_ {n}\ izquierda (\ cos\ dfrac {2 n\ pi t} {b-a}\ cos\ dfrac {2 n\ pi a} {b-a} +\ sin\ dfrac {2 n\ pi t} {b-a}\ sin\ dfrac {2 n\ pi a} {b-a}\ derecho)\ derecho. \\
&\ izquierda. +b_ {n}\ izquierda (\ sin\ dfrac {2 n\ pi t} {b-a}\ cos\ dfrac {2 n\ pi a} {b-a} -\ cos\ dfrac {2 n\ pi t} {b-a} {b-a}\ sin\ dfrac {2 n\ pi a} {b-a}\ derecha)\ derecha]\\
=&\ dfrac {_ {0}} {2} +\ suma_ {n=1} ^ {\ infty}\ izquierda [\ cos\ dfrac {2 n\ pi t} {b-a}\ izquierda (a_ {n}\ cos\ dfrac {2 n\ pi a} {b-a} -b_ {n}\ sin\ dfrac {2 n\ pi a} {b-a}\ derecha)\ a la derecha. \\
&\ izquierda. +\ sin\ dfrac {2 n\ pi t} {b-a}\ izquierda (a_ {n}\ sin\ dfrac {2 n\ pi a} {b-a} +b_ {n}\ cos\ dfrac {2 n\ pi a} {b-a}\ derecha)\ derecha].
\ end {alineado}\ etiqueta {5.44}\]
Definir\(A_{0}=a_{0}\) y
\ [\ begin {array} {r}
A_ {n}\ equiv a_ {n}\ cos\ dfrac {2 n\ pi a} {b-a} -b_ {n}\ sin\ dfrac {2 n\ pi a} {b-a}\\
b_ {n}\ equiv a_ {n}\ sin\ dfrac {2 n\ pi a} {b-a} +b_ {n}\ cos\ dfrac {2 n\ pi a} {b-a}
\ fin {array}\ etiqueta {5.45}\]
llegamos a la forma más deseable para la representación en serie de Fourier de una función definida en el intervalo\([a, b]\).
\[g(t) \sim \dfrac{A_{0}}{2}+\sum_{n=1}^{\infty}\left[A_{n} \cos \dfrac{2 n \pi t}{b-a}+B_{n} \sin \dfrac{2 n \pi t}{b-a}\right] . \label{5.46} \]
A continuación necesitamos encontrar expresiones para los coeficientes de Fourier. Insertamos las expresiones conocidas para\(a_{n}\) y\(b_{n}\) y reorganizamos. Primero, observamos que bajo la transformación\(x=2 \pi \dfrac{t-a}{b-a}\) tenemos
\ [\ begin {alineado}
a_ {n} &=\ dfrac {1} {\ pi}\ int_ {0} ^ {2\ pi} f (x)\ cos n x d x\\
&=\ dfrac {2} {b-a}\ int_ {a} ^ {b} g (t)\ cos\ dfrac {2 n\ pi (t-a)} b-{ a} d t
\ final {alineado}\ etiqueta {5.47}\]
y
\ [\ begin {alineado}
b_ {n} &=\ dfrac {1} {\ pi}\ int_ {0} ^ {2\ pi} f (x)\ cos n x d x\\
&=\ dfrac {2} {b-a}\ int_ {a} ^ {b} g (t)\ sin\ dfrac {2 n\ pi (t-a)} b-{ a} d t
\ final {alineado}\ etiqueta {5.48}\]
Luego, insertando estas integrales\(A_{n}\), combinando integrales y haciendo uso de la fórmula de adición para el coseno de la suma de dos ángulos, obtenemos
\ [\ begin {alineado}
A_ {n} &\ equiv a_ {n}\ cos\ dfrac {2 n\ pi a} {b-a} -b_ {n}\ sin\ dfrac {2 n\ pi a} {b-a}\\
&=\ dfrac {2} {b-a}\ int_ {a} ^ {b} g (t)\ izquierda [\ cos\ dfrac {2 n\ pi (t-a)} {b-a}\ cos\ dfrac {2 n\ pi a} {b-a} -\ sin\ dfrac {2 n\ pi (t-a)} {b-a}\ sin\ dfrac {2 n\ pi a} {b-a}\ derecha] d t\
&=\ dfrac {2} {b-a}\ int_ {a} ^ {b} g (t)\ cos\ dfrac {2 n\ pi t} {b-a} d t.
\ end {alineado}\ etiqueta {5.49}\]
Un cómputo similar da
\[B_{n}=\dfrac{2}{b-a} \int_{a}^{b} g(t) \sin \dfrac{2 n \pi t}{b-a} d t . \label{5.50} \]
Resumiendo, hemos demostrado que:
La representación de la serie de Fourier de\(f(x)\) definido en\([a, b]\) cuando existe, viene dada por
\[f(x) \sim \dfrac{a_{0}}{2}+\sum_{n=1}^{\infty}\left[a_{n} \cos \dfrac{2 n \pi x}{b-a}+b_{n} \sin \dfrac{2 n \pi x}{b-a}\right]. \label{5.51} \]
con coeficientes de Fourier
\ [\ begin {array} {ll}
a_ {n} =\ dfrac {2} {b-a}\ int_ {a} ^ {b} f (x)\ cos\ dfrac {2 n\ pi x} {b-a} d x. & n=0,1,2,\ lpuntos,\\
b_ {n} =\ dfrac {2} {b-a}\ int_ {a} ^ {b} f (x)\ sin\ dfrac {2 n\ pi x} {b-a} d x. & n=1,2,\ lpuntos.
\ end {array}\ label {5.52}\]


