5.4: Serie Seno y Coseno
- Page ID
- 118962
En los dos últimos ejemplos (\(f(x) = |x|\)y\(f(x) = x\) en adelante\([−\pi, \pi]\)) hemos visto representaciones de series de Fourier que contienen solo términos sinusoidales o coseno. Como sabemos, las funciones sinusoidales son funciones impares y, por lo tanto, suman a funciones impares. Del mismo modo, las funciones coseno suman a funciones pares. Tales ocurrencias ocurren a menudo en la práctica. Las representaciones de Fourier que involucran solo senos se llaman series sinusoidales y las que involucran solo cosenos (y el término constante) se llaman series coseno.
Otro resultado interesante, basado en estos ejemplos, es que las funciones originales,\(|x|\) y\(x\) coinciden en el intervalo\([0, \pi]\). Obsérvese de las Figuras 5.7-5.9 que sus representaciones en serie de Fourier también lo hacen. Así, se pueden utilizar más de una serie para representar funciones definidas en intervalos finitos. Todo lo que necesitan hacer es estar de acuerdo con la función a lo largo de ese intervalo en particular. A veces una de estas series es más útil porque tiene propiedades adicionales necesarias en la aplicación dada.
Hemos hecho las siguientes observaciones a partir de los ejemplos anteriores:
- Hay varias representaciones trigonométricas de series para una función definida en un intervalo finito.
- Las funciones impares en un intervalo simétrico están representadas por series sinusoidales y las funciones pares en un intervalo simétrico están representadas por series coseno.
Estas dos observaciones están relacionadas y son objeto de esta sección. Comenzamos definiendo una función\(f(x)\) en el intervalo\([0, L]\). Hemos visto que la representación en serie de Fourier de esta función parece converger a una extensión periódica de la función.
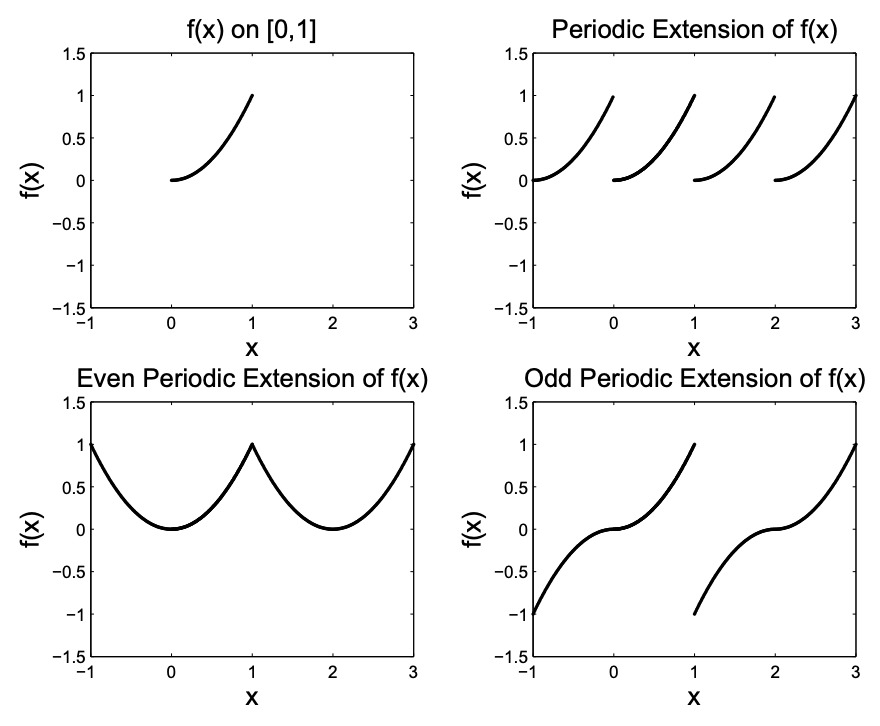
En la Figura 5.10 mostramos una función definida en\([0, 1]\). A la derecha está su extensión periódica a todo el eje real. Esta representación tiene un periodo de\(L = 1\). La gráfica inferior izquierda se obtiene reflejando primero\(f\) alrededor del\(y\) eje -para convertirlo en una función par y luego graficando la extensión periódica de esta nueva función. Su periodo será\(2L = 2\). Finalmente, en la última gráfica volteamos la función alrededor de cada eje y graficamos la extensión periódica de la nueva función impar. También tendrá un periodo de\(2L = 2\).
En general, obtenemos tres representaciones periódicas diferentes. Para distinguirlos nos referiremos simplemente como las extensiones periódicas, pares e impares. Ahora, comenzando por\(f(x)\) definido en\([0, L]\), nos gustaría determinar las representaciones de la serie de Fourier que conducen a estas extensiones. [Para una fácil referencia, los resultados se resumen en la Tabla 5.2] Ya hemos visto que la extensión periódica de\(f(x)\) se obtiene a través de la representación de la serie de Fourier en la Ecuación (5.53).
|
Serie de Fourier en\([0, L]\) \[f(x) \sim \dfrac{a_{0}}{2}+\sum_{n=1}^{\infty}\left[a_{n} \cos \dfrac{2 n \pi x}{L}+b_{n} \sin \dfrac{2 n \pi x}{L}\right] \label{5.53} \] \ [\ comenzar {reunido} |
|
Serie coseno de Fourier en\([0, L]\) \[f(x) \sim a_{0} / 2+\sum_{n=1}^{\infty} a_{n} \cos \dfrac{n \pi x}{L} \label{5.55} \] donde \[a_{n}=\dfrac{2}{L} \int_{0}^{L} f(x) \cos \dfrac{n \pi x}{L} d x . \quad n=0,1,2, \ldots \label{5.56} \] |
|
Serie sinusoidal de Fourier encendida\([0, L]\) \[f(x) \sim \sum_{n=1}^{\infty} b_{n} \sin \dfrac{n \pi x}{L} \label{5.57} \] donde \[b_{n}=\dfrac{2}{L} \int_{0}^{L} f(x) \sin \dfrac{n \pi x}{L} d x . \quad n=1,2, \ldots \label{5.58} \] |
Cuadro 5.2. Representaciones en serie de coseno y coseno de Fourier en\([0, L]\)
Dado\(f(x)\) definido en\([0, L]\), la extensión periódica par se obtiene simplemente calculando la representación de la serie de Fourier para la función par
\ [f_ {e} (x)\ equiv\ left\ {\ begin {array} {c}
f (x),\ quad 0<x<L\\
f (-x) -l<x<0
\ end {array}\ right. \ label {5.59}\]
Dado que\(f_{e}(x)\) es una función par en un intervalo simétrico\([-L, L]\), esperamos que la serie resultante de Fourier no contenga términos sinusoidales. Por lo tanto, la expansión en serie estará dada por [Usar el caso general en (5.51) con\(a=-L\) y\(b=L\).]
\[f_{e}(x) \sim \dfrac{a_{0}}{2}+\sum_{n=1}^{\infty} a_{n} \cos \dfrac{n \pi x}{L} \label{5.60} \]
con coeficientes de Fourier
\[a_{n}=\dfrac{1}{L} \int_{-L}^{L} f_{e}(x) \cos \dfrac{n \pi x}{L} d x . \quad n=0,1,2, \ldots \label{5.61} \]
Sin embargo, podemos simplificar esto señalando que el integrando es parejo y el intervalo de integración puede ser reemplazado por\([0, L]\). En este intervalo\(f_{e}(x)=f(x)\). Entonces, tenemos la Serie Cosine Representación de\(f(x)\) for\(x \in[0, L]\) se da como
\[f(x) \sim \dfrac{a_{0}}{2}+\sum_{n=1}^{\infty} a_{n} \cos \dfrac{n \pi x}{L} \label{5.62} \]
donde
\[a_{n}=\dfrac{2}{L} \int_{0}^{L} f(x) \cos \dfrac{n \pi x}{L} d x . \quad n=0,1,2, \ldots \label{5.63} \]
Del mismo modo, dado\(f(x)\) definido en\([0, L]\), la extensión periódica impar se obtiene simplemente calculando la representación de la serie de Fourier para la función impar
\ [f_ {o} (x)\ equiv\ left\ {\ begin {array} {c}
f (x),\ quad 0<x<l\\
-f (-x) -l<x<0
\ end {array}\ right. \ label {5.64}\]
La expansión de la serie resultante conduce a definir la representación de la serie sinusoidal de\(f(x)\) for\(x \in[0, L]\) as
\[f(x) \sim \sum_{n=1}^{\infty} b_{n} \sin \dfrac{n \pi x}{L} \label{5.65} \]
donde
\[b_{n}=\dfrac{2}{L} \int_{0}^{L} f(x) \sin \dfrac{n \pi x}{L} d x . \quad n=1,2, \ldots \label{5.66} \]
En la Figura 5.10 de hecho proporcionamos gráficas de las diversas extensiones de la función\(f(x)=x^{2}\) para\(x \in[0,1]\). Determinemos las representaciones de las extensiones periódicas, pares e impares de esta función.
Para variar, usaremos un paquete CAS (Computer Algebra System) para hacer las integrales. En este caso podemos usar Maple. Un código general para hacer esto para la extensión periódica se muestra en la Tabla 5.3
> restart:
> L:=1:
> f:=x^2:
> assume(n,integer):
> a0:=2/L*int(f,x=0..L);
a0 := 2/3
> an:=2/L*int(f*cos(2*n*Pi*x/L),x=0..L);
1
an := -------
2 2
n~ Pi
> bn:=2/L*int(f*sin(2*n*Pi*x/L),x=0..L);
1
bn := - -----
n~ Pi
> F:=a0/2+sum((1/(k*Pi)^2)*cos(2*k*Pi*x/L) -1/(k*Pi)*sin(2*k*Pi*x/L),k=1..50):
> plot(F,x=-1..3,title=‘Periodic Extension‘, titlefont=[TIMES,ROMAN,14],font=[TIMES,ROMAN,14]);
Cuadro 5.3. Código de arce para calcular coeficientes de Fourier y trazar sumas parciales de la serie de Fourier.
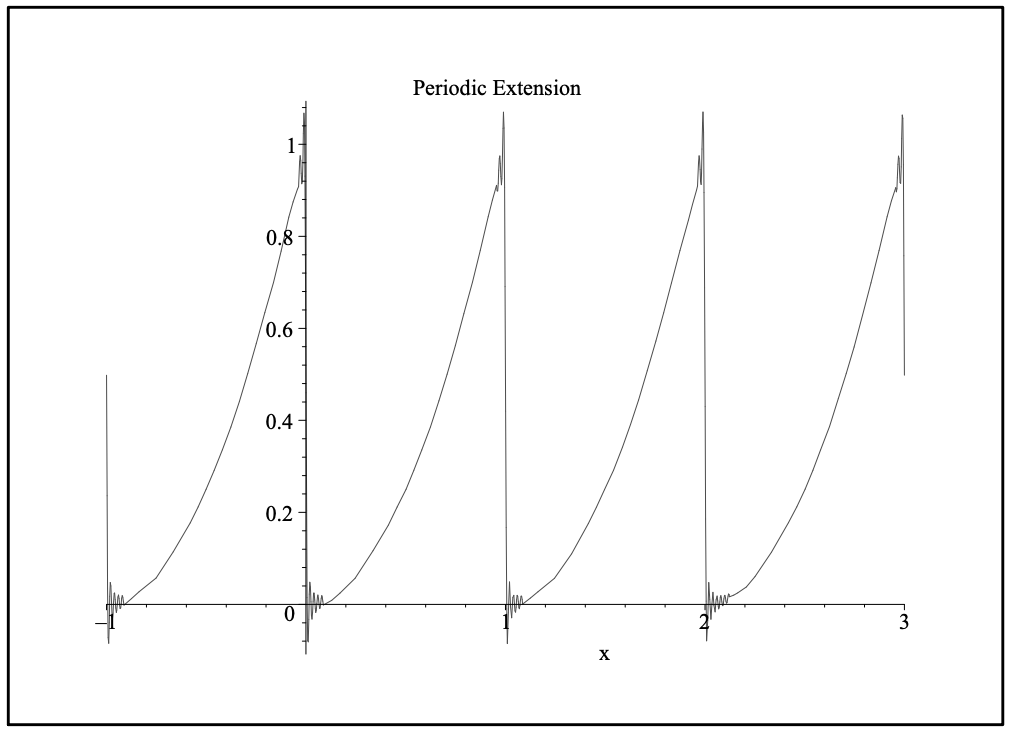
Usando el código anterior, tenemos eso\(a_{0}=\dfrac{2}{3} \quad a_{n}=\dfrac{1}{n^{2} \pi^{2}}\) y\(b_{n}=-\dfrac{1}{n \pi}\). Así, la serie resultante se da como
\[f(x) \sim \dfrac{1}{3}+\sum_{n=1}^{\infty}\left[\dfrac{1}{n^{2} \pi^{2}} \cos 2 n \pi x-\dfrac{1}{n \pi} \sin 2 n \pi x\right]. \nonumber \]
En la Figura 5.11 vemos la suma de los primeros 50 términos de esta serie. Generalmente, vemos que la serie parece estar convergiendo a la extensión periódica de\(f\). Parece haber algunos problemas con la convergencia alrededor de los valores enteros de\(x\). Más adelante veremos que esto se debe a las discontinuidades en la extensión periódica y el sobreimpulso resultante es referido como el fenómeno de Gibbs que se discute en el apéndice.
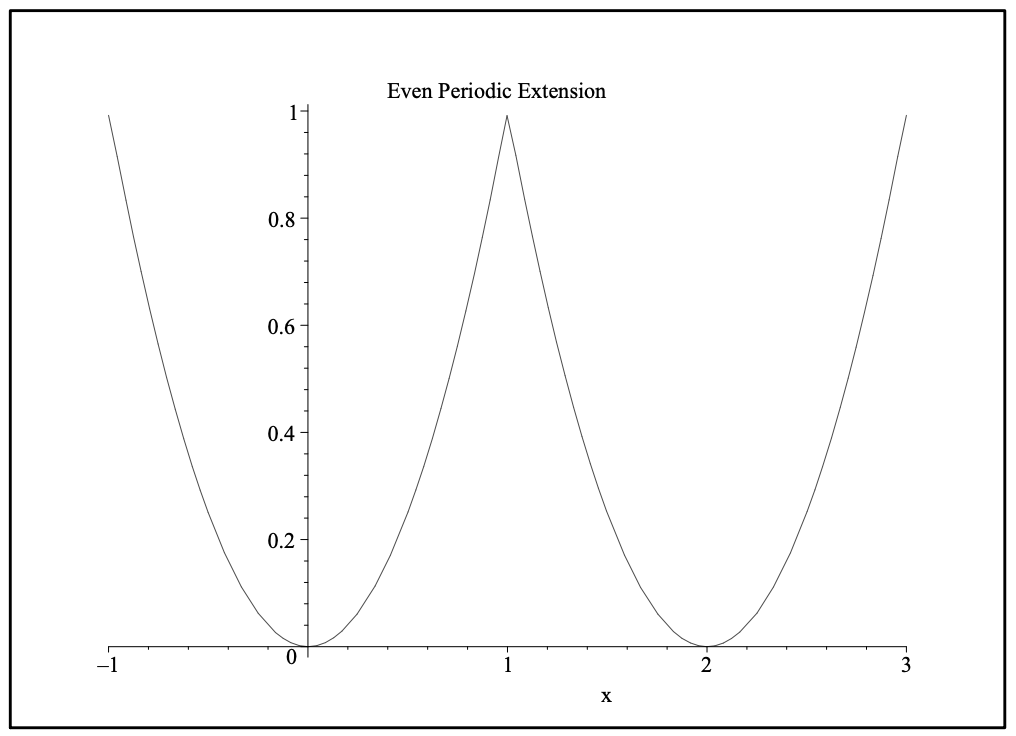
En este caso calculamos\(a_{0}=\dfrac{2}{3}\) y\(a_{n}=\dfrac{4(-1)^{n}}{n^{2} \pi^{2}}\). Por lo tanto, tenemos
\[f(x) \sim \dfrac{1}{3}+\dfrac{4}{\pi^{2}} \sum_{n=1}^{\infty} \dfrac{(-1)^{n}}{n^{2}} \cos n \pi x \nonumber \]
En la Figura 5.12 vemos la suma de los primeros 50 términos de esta serie. En este caso la convergencia parece ser mucho mejor que en el caso de extensión periódica. También vemos que está convergiendo a la extensión par.
Por último, nos fijamos en la serie sinusoidal para esta función. Nos encontramos con eso\(b_{n}= -\dfrac{2}{n^{3} \pi^{3}}\left(n^{2} \pi^{2}(-1)^{n}-2(-1)^{n}+2\right)\). Por lo tanto,
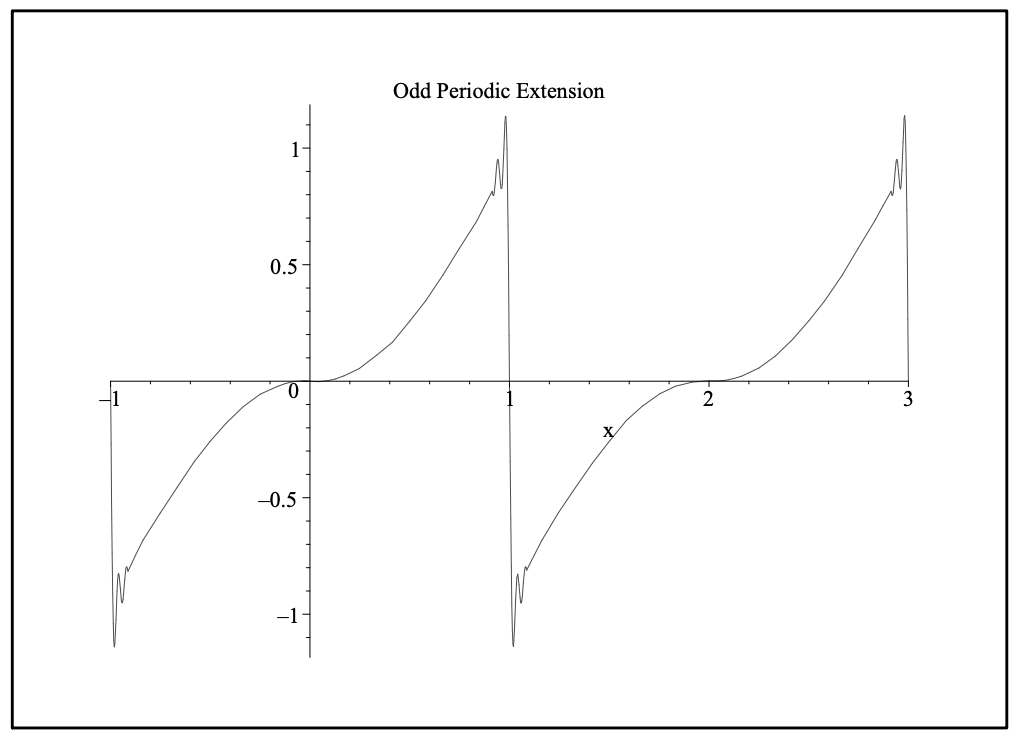
\[f(x) \sim-\dfrac{2}{\pi^{3}} \sum_{n=1}^{\infty} \dfrac{1}{n^{3}}\left(n^{2} \pi^{2}(-1)^{n}-2(-1)^{n}+2\right) \sin n \pi x. \nonumber \]
Una vez más vemos discontinuidades en la extensión como se ve en la Figura 5.13. Sin embargo, hemos verificado que nuestra serie sinusoidal parece estar convergiendo a la extensión impar como esbozamos por primera vez en la Figura 5.10.