5.5: Apéndice- El Fenómeno Gibbs

Hemos visto que cuando hay una discontinuidad de salto en la extensión periódica de nuestras funciones, si la función originalmente tenía una discontinuidad o desarrolló una debido a un desajuste en los valores de los puntos finales. Esto se puede apreciar en las Figuras 5.9, 5.11 y 5.13. La serie de Fourier tiene dificultades para converger en el punto de discontinuidad y estas gráficas de la serie de Fourier muestran un sobreimpulso distinto que no desaparece. A esto se le llama el fenómeno Gibbs y se puede calcular la cantidad de sobreimpulso.

En uno de nuestros primeros ejemplos, Ejemplo 5.6, encontramos la representación en serie de Fourier de la función definida por partes

\ (f (x) =\ left\ {\ begin {array} {c}
1,\ quad 0<x<\ pi\\
-1,\ pi<x<2\ pi
\ end {array}\ right.\)

ser

\[f(x) \sim \dfrac{4}{\pi} \sum_{k=1}^{\infty} \dfrac{\sin (2 k-1) x}{2 k-1} . \nonumber \]

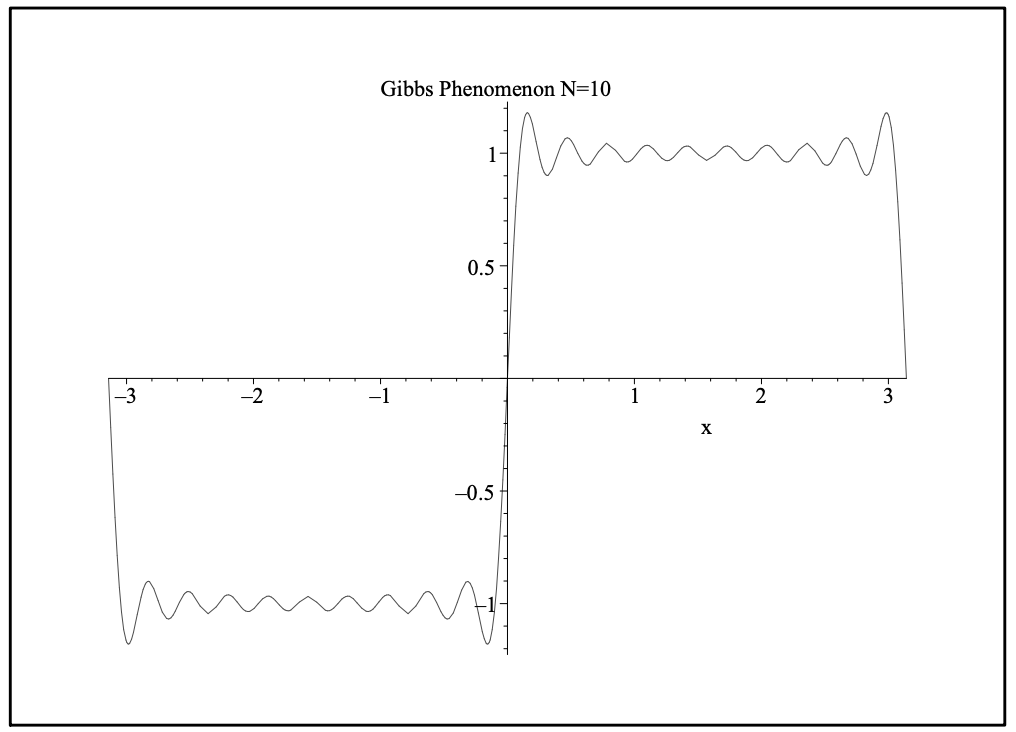
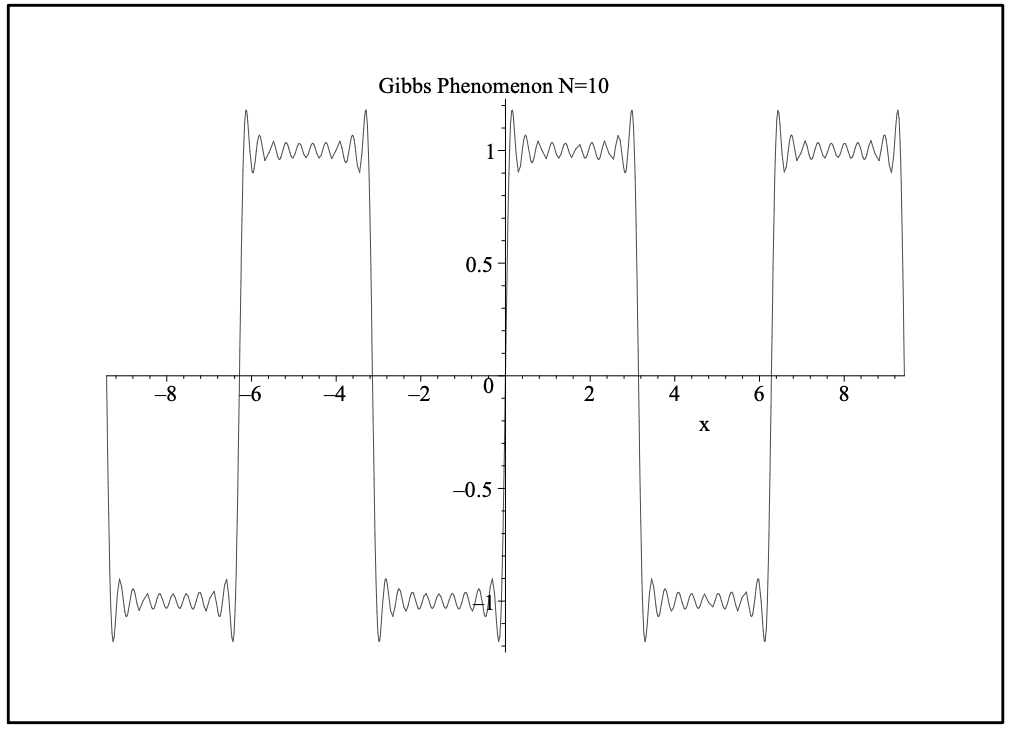
En la Figura 5.14 mostramos la suma de los diez primeros términos. Tenga en cuenta los meneamientos, rebasamientos y debajo de los brotes cerca\(x=0, \pm \pi\). Estos se ven más cuando trazamos la representación para\(x \in[-3 \pi, 3 \pi]\), como se muestra en la Figura 5.15. Observamos que los rebasamientos y subbrotes ocurren a discontinuidades en la extensión periódica de\(f(x)\). Estos ocurren siempre que\(f(x)\) tenga una discontinuidad o si los valores de\(f(x)\) en los puntos finales del dominio no coinciden.

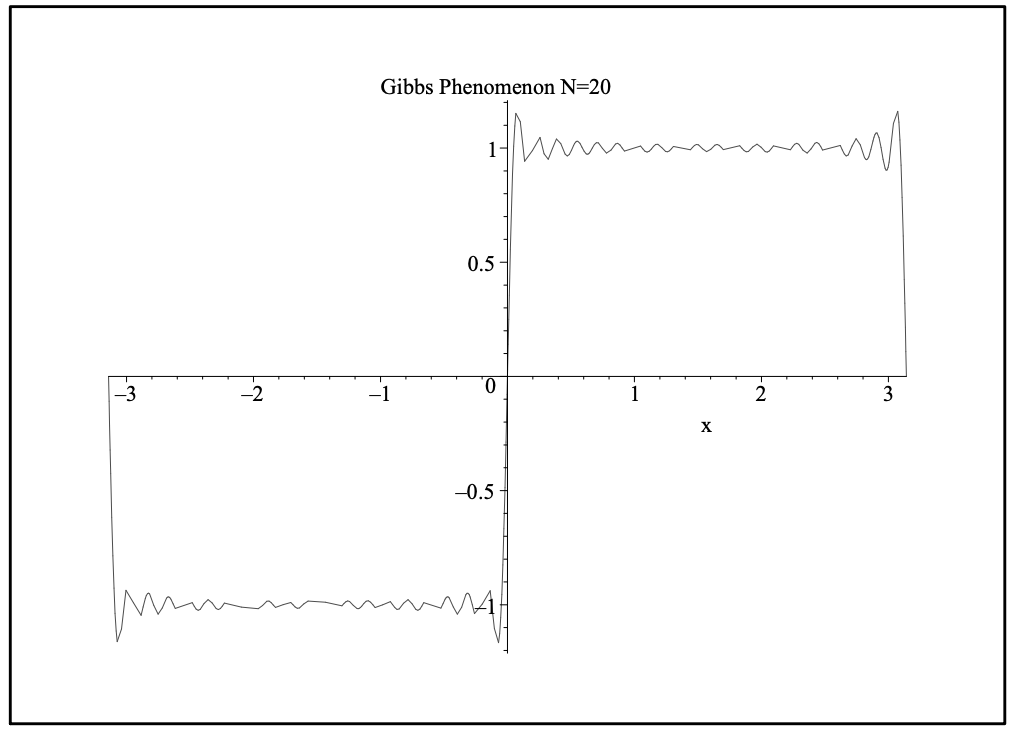
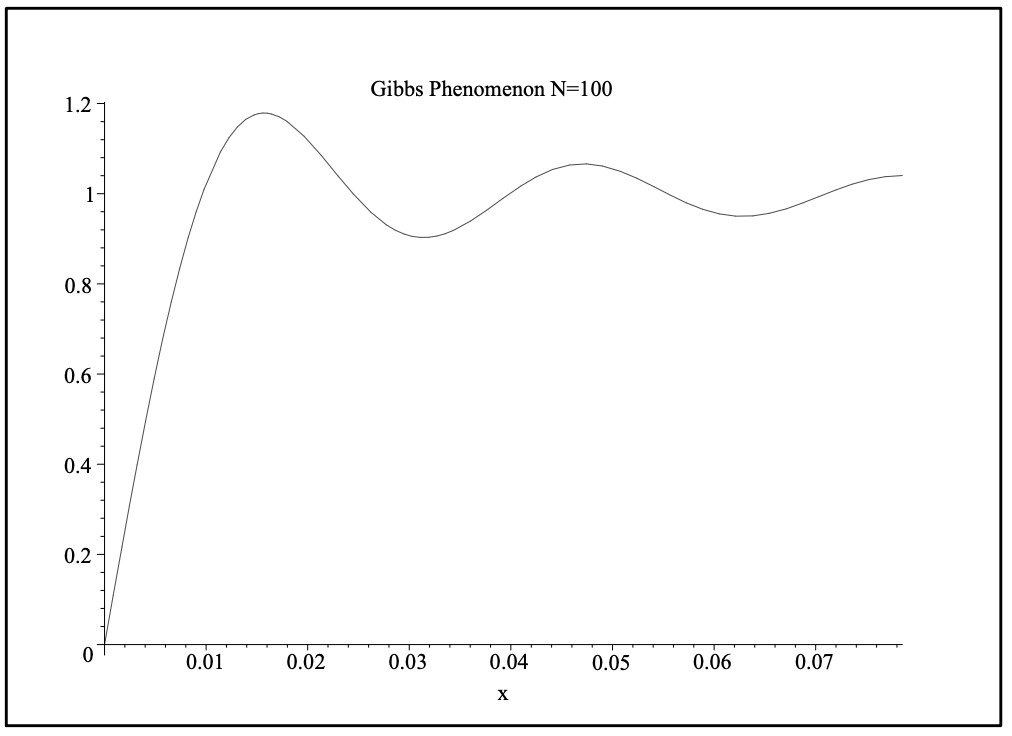
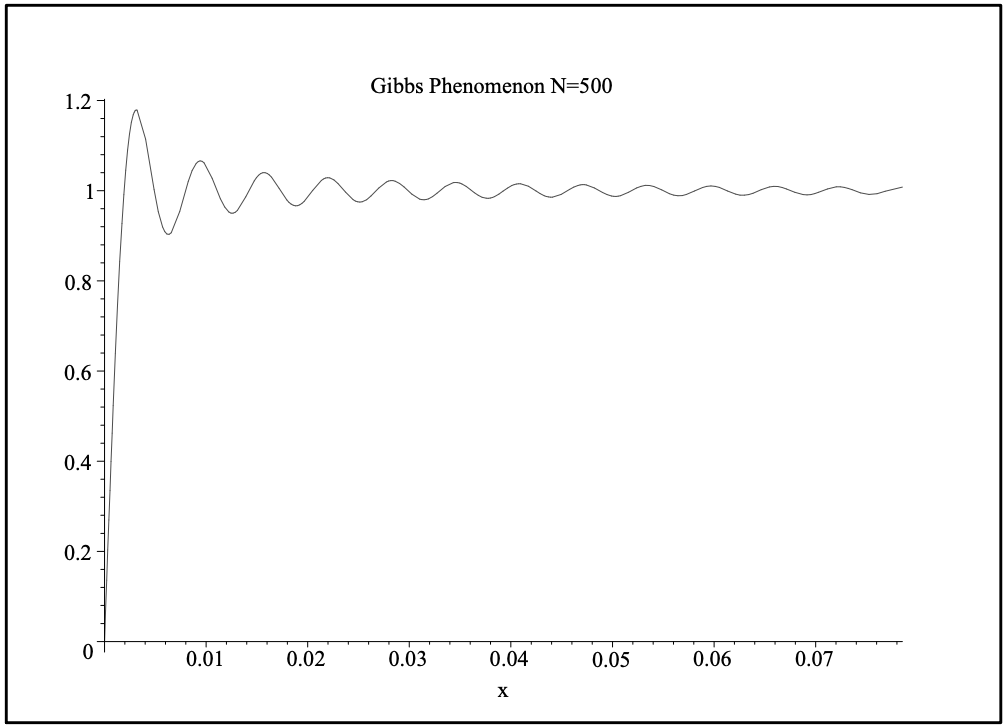
Uno podría esperar que solo necesitamos agregar más términos. En la Figura 5.16 se muestra la suma de veinte términos. Obsérvese que la suma parece converger mejor para puntos alejados de las discontinuidades. Pero, los rebasamientos y subbrotes siguen presentes. En las Figuras 5.17 y 5.18 se muestran gráficas ampliadas del sobreimpulso a\(x=0\) para\(N=100\) y\(N=500\), respectivamente. Vemos que el sobreimpulso persiste. El pico se encuentra aproximadamente a la misma altura, pero su ubicación parece estar cada vez más cerca del origen. Mostraremos cómo se puede estimar el tamaño del sobreimpulso.

Figura 5.14. La representación en serie de Fourier de una función de paso en\([−\pi, \pi]\) for\(N = 10\).

Podemos estudiar el fenómeno de Gibbs observando las sumas parciales de series trigonométricas generales de Fourier para funciones\(f(x)\) definidas en el intervalo\([−L, L]\). Escribiendo las sumas parciales, insertando los coeficientes de Fourier y reordenando, tenemos

Figura 5.15. La representación en serie de Fourier de una función de paso en\([−\pi, \pi]\) para\(N = 10\) graficada\([−3\pi, 3\pi]\) al mostrar la periodicidad.

\(S_{N}(x)=a_{0}+\sum_{n=1}^{N}\left[a_{n} \cos \dfrac{n \pi x}{L}+b_{n} \sin \dfrac{n \pi x}{L}\right]\)

Figura 5.16. La representación en serie de Fourier de una función de paso en\([-\pi, \pi]\) for\(N=20\).

Figura 5.17. La representación en serie de Fourier de una función de paso en\([−\pi, \pi]\) for\(N = 100\).

\ [\ begin {alineado}
=&\ dfrac {1} {2 L}\ int_ {-L} ^ {L} f (y) d y+\ sum_ {n=1} ^ {N}\ left [\ left (\ dfrac {1} {L}\ int_ {-L} ^ {L} f (y)\ cos\ dfrac {n\ pi y} {L}} d y\ derecha)\ cos\ dfrac {n\ pi x} {L}\ derecha. \\
&\ izquierda. +\ izquierda (\ dfrac {1} {L}\ int_ {-L} ^ {L} f (y)\ sin\ dfrac {n\ pi y} {L} d y\ derecha)\ sin\ dfrac {n\ pi x} {L}\ derecha]\\
=&\ dfrac {1} {L}\ int_ {-L} ^ {L} izquierda\\ {\ dfrac {1} {2} +\ sum_ {n=1} ^ {N}\ izquierda (\ cos\ dfrac {n\ pi y} {L}\ cos\ dfrac {n\ pi x} {L} +\ sin\ dfrac {n\ pi y} {L}\ sin\ dfrac {n\ pi x} {L}\ derecha)\ derecha\} f (y) d y\\
=&\ dfrac {1} {L}\ int_ {-L} ^ {L}\ izquierda\ {\ dfrac {1} {2} +\ sum_ {n=1} ^ {N}\ cos\ dfrac {n\ pi (y-x)} {L}\ derecha\} f (y) d y\
\ equiv &\ dfrac {1} L}\ int_ {-L} ^ {L} D_ {N} (y-x) f (y) d y.
\ end {alineado}\ etiqueta {5.67}\]

Hemos definido

\[D_{N}(x)=\dfrac{1}{2}+\sum_{n=1}^{N} \cos \dfrac{n \pi x}{L}, \nonumber \]

que se llama el\(N\) -ésimo Kernel de Dirichlet. Ahora probamos

Figura 5.18. La representación en serie de Fourier de una función de paso en\([−\pi, \pi]\) for\(N = 500\).

Proposición:

\[D_{n}(x)= \begin{cases}\dfrac{\sin \left(\left(n+\dfrac{1}{2}\right) \dfrac{\pi x}{L}\right)}{2 \sin \dfrac{\pi x}{2 L}}, & \sin \dfrac{\pi x}{2 L} \neq 0 \\ n+\dfrac{1}{2}, & \sin \dfrac{\pi x}{2 L}=0\end{cases} \nonumber \]

Prueba: Dejar\(\theta=\dfrac{\pi x}{L}\) y multiplicar\(D_{n}(x)\) por\(2 \sin \dfrac{\theta}{2}\) para obtener:

\ [\ begin {alineado}
2\ sin\ dfrac {\ theta} {2} D_ {n} (x) =& 2\ sin\ dfrac {\ theta} {2}\ izquierda [\ dfrac {1} {2} +\ cos\ theta+\ cdots+\ cos n\ theta\ derecha]\\\
=&\ sin\ dfrac {theta\ theta} {2} +2\ cos\ theta\ sin\ dfrac {\ theta} {2} +2\ cos 2\ theta\ sin\ dfrac {\ theta} {2} +\ cdots+2\ cos n\ theta\ sin\ dfrac {\ theta} {2}\\
=&\ sin\ dfrac {\ theta} {2} +\ izquierda (\ sin\ dfrac {3\ theta} {2} -\ sin\ dfrac {\ theta} {2}\ derecha) +\ izquierda (\ sin\ dfrac {5\ theta} {2} -\ sin\ dfrac {3\ theta} {2}\ derecha) +\ cdots\\
&+\ izquierda [\ sin\ izquierda (n+\ dfrac {1} {2}\ derecha)\ theta-\ sin\ izquierda (n-\ dfrac {1} {2}\ derecha)\ theta\ derecha]\\
=&\ sin\ izquierda (n+\ dfrac {1} {2}\ derecha)\ theta
\ final {alineado}\ etiqueta {5.68}\]

Por lo tanto,

\[2 \sin \dfrac{\theta}{2} D_{n}(x)=\sin \left(n+\dfrac{1}{2}\right) \theta \nonumber \]

o si\(\sin \dfrac{\theta}{2} \neq 0\)

\[D_{n}(x)=\dfrac{\sin \left(n+\dfrac{1}{2}\right) \theta}{2 \sin \dfrac{\theta}{2}}, \quad \theta=\dfrac{\pi x}{L} \nonumber \]

Si\(\sin \dfrac{\theta}{2}=0\), entonces se necesita aplicar la Regla de L'Hospital:

\ [\ comenzar {alineado}
\ lim _ {\ theta\ fila derecha 2 m\ pi}\ dfrac {\ sin\ izquierda (n+\ dfrac {1} {2}\ derecha)\ theta} {2\ sin\ dfrac {\ theta} {2}} &=\ lim _ {\ theta\ fila derecha 2 m\ pi}\ dfrac {izquierda\ (n+\ dfrac {1} {2}\ derecha)\ cos\ izquierda (n+\ dfrac {1} {2}\ derecha)\ theta} {\ cos\ dfrac {\ theta} {2}}\\
&=\ dfrac { \ izquierda (n+\ dfrac {1} {2}\ derecha)\ cos (2 m n\ pi+m\ pi)} {\ cos m\ pi}\\
&=n+\ dfrac {1} {2}.
\ end {alineado}\ etiqueta {5.69}\]

Observamos además que\(D_{N}(x)\) es periódico con periodo\(2 L\) y es una función par.

Hasta el momento, hemos encontrado que

\[S_{N}(x)=\dfrac{1}{L} \int_{-L}^{L} D_{N}(y-x) f(y) d y \label{5.70} \]

Ahora, haz la sustitución\(\xi=y-x\). Entonces,

\ [\ begin {alineado}
S_ {N} (x) &=\ dfrac {1} {L}\ int_ {-L-x} ^ {L-x} D_ {N} (\ xi) f (\ xi+x) d\ xi\\
&=\ dfrac {1} {L}\ int_ {-L} ^ {L} D_ {N} (\ xi) f (\ xi+x) d\ xi
\ final {alineado}\ etiqueta {5.71}\]

En la segunda integral hemos hecho uso del hecho de que\(f(x)\) y\(D_{N}(x)\) son periódicos con periodo\(2 L\) y desplazado el intervalo de nuevo a\([-L, L]\).

Ahora divide la integración y usa el hecho de que\(D_{N}(x)\) es una función par. Entonces,

\ [\ begin {alineado}
S_ {N} (x) &=\ dfrac {1} {L}\ int_ {-L} ^ {0} D_ {N} (\ xi) f (\ xi+x) d\ xi+\ dfrac {1} {L}\ int_ {0} ^ {L} D_ {N} (\ xi) f (\ xi+x) d\ xi\\
&=\ dfrac {1} {L}\ int_ {0} ^ {L} [f (x-\ xi) +f (\ xi+x)] D_ {N} (\ xi) d\ xi
\ final {alineado}\ etiqueta {5.72}\]

Podemos utilizar este resultado para estudiar el fenómeno de Gibbs siempre que ocurra. En particular, sólo nos concentraremos en nuestro ejemplo anterior. A saber,

\ (f (x) =\ left\ {\ begin {array} {c}
1,\ quad 0<x<\ pi\\
-1,\ pi<x<2\ pi
\ end {array}\ right.\)

Para este caso, tenemos

\[S_{N}(x)=\dfrac{1}{\pi} \int_{0}^{\pi}[f(x-\xi)+f(\xi+x)] D_{N}(\xi) d \xi \label{5.73} \]

para

\[D_{N}(x)=\dfrac{1}{2}+\sum_{n=1}^{N} \cos n x . \nonumber \]

Además, se puede demostrar que

\ (f (x-\ xi) +f (\ xi+x) =\ izquierda\ {\ comenzar {matriz} {c}
2,\ quad 0\ leq\ xi<x\\
0,\ quad x\ leq\ xi<\ pi-x\
-2,\ pi-x\ leq\ xi<\ pi
\ end {array}\ derecha.\)

Por lo tanto, tenemos

\ [\ begin {alineado}
S_ {N} (x) &=\ dfrac {2} {\ pi}\ int_ {0} ^ {x} D_ {N} (\ xi) d\ xi-\ dfrac {2} {\ pi}\ int_ {\ pi-x} ^ {\ pi} D_ {N} (\ xi) d\ xi\
&= d= frac {2} {\ pi}\ int_ {0} ^ {x} D_ {N} (z) d z+\ dfrac {2} {\ int_ {0} ^ {x}} D_ {N} (\ pi-z) d z
\ final {alineado}\ etiqueta {5.74}\]

Aquí hicimos la sustitución\(z=\pi-\xi\) en la segunda integral. El kernel de Dirichlet en la proposición para\(L=\pi\) viene dado por

\[D_{N}(x)=\dfrac{\sin \left(N+\dfrac{1}{2}\right) x}{2 \sin \dfrac{x}{2}} . \nonumber \]

Para\(N\) grandes, tenemos\(N+\dfrac{1}{2} \approx N\), y para pequeños\(x\), tenemos\(\sin \dfrac{x}{2} \approx \dfrac{x}{2}\). Entonces, bajo estos supuestos,

\[D_{N}(x) \approx \dfrac{\sin N x}{x} . \nonumber \]

Por lo tanto,

\[S_{N}(x) \rightarrow \dfrac{2}{\pi} \int_{0}^{x} \dfrac{\sin N \xi}{\xi} d \xi \nonumber \]

Si queremos determinar las ubicaciones de los mínimos y máximos, donde ocurren el subimpulso y el sobreimpulso, entonces aplicamos la primera prueba derivada para extremos a\(S_{N}(x)\). Por lo tanto,

\[\dfrac{d}{d x} S_{N}(x)=\dfrac{2}{\pi} \dfrac{\sin N x}{x}=0 . \nonumber \]

Los extremos ocurren para\(N x=m \pi, m=\pm 1, \pm 2, \ldots\) Uno puede demostrar que hay un máximo en\(x=\pi / N\) y un mínimo para\(x=2 \pi / N\). El valor para el sobreimpulso se puede calcular como

\ [\ begin {alineado}
S_ {N} (\ pi/N) &=\ dfrac {2} {\ pi}\ int_ {0} ^ {\ pi/N}\ dfrac {\ sin N\ xi} {\ xi} d\ xi\\
&=\ dfrac {2} {\ pi}\ int_ {0} ^ {\ pi}\ dfrac\ sin t} {t} d t\\
&=\ dfrac {2} {\ pi}\ nombreoperador {Si} (\ pi)\\
&=1.178979744\ lpuntos
\ end {alineado}\ etiqueta {5.75}\]

Obsérvese que este valor es independiente\(N\) y se da en términos de la integral sinusoidal,

\[\operatorname{Si}(x) \equiv \int_{0}^{x} \dfrac{\sin t}{t} d t \nonumber \]