7.1: Polinomios ortogonales clásicos

Comenzamos por señalar que la secuencia de funciones\(\left\{1, x, x^{2}, \ldots\right\}\) es una base de funciones linealmente independientes. De hecho, por el Teorema de Aproximación Stone-Weierstrass este conjunto es una base de\(L_{\sigma}^{2}(a, b)\), el espacio de las funciones integrables cuadradas sobre el intervalo\([a, b]\) relativo al peso\(\sigma(x)\). Estamos familiarizados con poder ampliar funciones sobre esta base, ya que las expansiones son solo representaciones de series de poder de las funciones,

\[f(x) \sim \sum_{n=0}^{\infty} c_{n} x^{n} . \nonumber \]

Sin embargo, esta base no es un conjunto ortogonal de funciones base. Uno puede ver esto fácilmente integrando el producto de dos funciones base pares, o dos impares, con $\ sigma (x) =1$ y\((a, b)=(-1,1)\). Por ejemplo,

\[\left\langle 1, x^{2}\right\rangle=\int_{-1}^{1} x^{0} x^{2} d x=\dfrac{2}{3} . \nonumber \]

Dado que hemos encontrado que las bases ortogonales han sido útiles para determinar los coeficientes para expansiones de funciones dadas, podríamos preguntar si es posible obtener una base ortogonal que involucre estas potencias de\(x\). ¡Por supuesto, las combinaciones finitas de estos elementos base son solo polinomios!

Bien, vamos a preguntar. “Dado un conjunto de vectores de base linealmente independientes, ¿se puede encontrar una base ortogonal del espacio dado?” La respuesta es sí. Recordamos del álgebra lineal introductoria, que en su mayoría cubre espacios vectoriales de dimensiones finitas, que existe un método para llevar a cabo esto llamado Proceso de Ortogonalización Gram-Schmidt. Recordaremos este proceso para vectores dimensionales finitos y luego generalizaremos a espacios funcionales.

Figura 7.1. El fundamento\(a_1, a_2\), y\(a_3\), de\(R^3\) considerado en el texto.

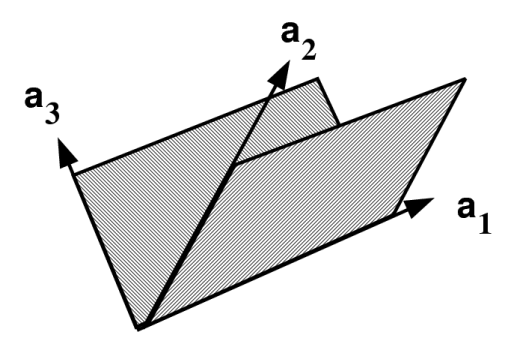
Supongamos que tenemos tres vectores que abarcan\(R^3\), dados por\(a_1, a_2,\) y\(a_3\) y mostrados en la Figura 7.1. Buscamos una base ortogonal\(e_1, e_2\), y\(e_3\), comenzando un vector a la vez.

Primero tomamos uno de los vectores base originales, digamos\(a_1\), y definimos

\[e_1 = a_1. \nonumber \]

Por supuesto, podríamos querer normalizar nuestros nuevos vectores base, por lo que denotaríamos tal vector normalizado con un “sombrero”:

\(\hat{e}_1 = \dfrac{e_1}{e_1}\),

donde\(e_{1}=\sqrt{\mathbf{e}_{1} \cdot \mathbf{e}_{1}}\).

A continuación, queremos determinar un\(\mathbf{e}_{2}\) que es ortogonal a\(\mathbf{e}_{1}\). Tomamos otro elemento de la base original,\(\mathbf{a}_{2}\). En la Figura 7.2 vemos la orientación de los vectores. Tenga en cuenta que el vector ortogonal deseado es\(\mathbf{e}_{2}\). Tenga en cuenta que se\(\mathbf{a}_{2}\) puede escribir como una suma de\(\mathbf{e}_{2}\) y la proyección de\(\mathbf{a}_{2}\) on\(\mathbf{e}_{1}\). Denotando esta proyección por\(\mathbf{p r}_{1} \mathbf{a}_{2}\), entonces tenemos

\[\mathbf{e}_{2}=\mathbf{a}_{2}-\mathbf{p r}_{1} \mathbf{a}_{2} . \label{7.1} \]

Recordamos la proyección de un vector sobre otro de nuestra clase de cálculo vectorial.

\[\mathbf{p r}_{1} \mathbf{a}_{2}=\dfrac{\mathbf{a}_{2} \cdot \mathbf{e}_{1}}{e_{1}^{2}} \mathbf{e}_{1} . \label{7.2} \]

Figura 7.2. Una trama de los vectores\(e_1, a_2\), y\(e_2\) necesaria para encontrar la proyección de\(a_2\), en\(e_1\).

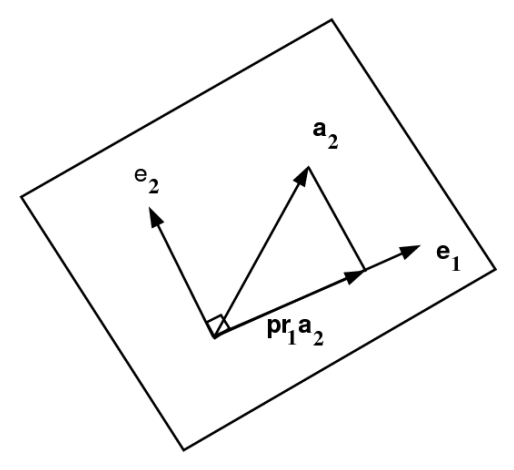
Tenga en cuenta que esto se prueba fácilmente escribiendo la proyección como un vector de longitud\(a_{2} \cos \theta\) en dirección\(\hat{\mathbf{e}}_{1}\), donde\(\theta\) está el ángulo entre\(\mathbf{e}_{1}\) y\(\mathbf{a}_{2}\). Usando la definición del producto punto,\(\mathbf{a} \cdot \mathbf{b}=a b \cos \theta\), sigue la fórmula de proyección.

Combinando Ecuaciones (7.1) - (7.2), encontramos que

\[\mathbf{e}_{2}=\mathbf{a}_{2}-\dfrac{\mathbf{a}_{2} \cdot \mathbf{e}_{1}}{e_{1}^{2}} \mathbf{e}_{1} . \label{7.3} \]

Es un asunto sencillo verificar que\(\mathbf{e}_{2}\) es ortogonal a\(\mathbf{e}_{1}\):

\ [\ begin {alineado}
\ mathbf {e} _ {2}\ cdot\ mathbf {e} _ {1} &=\ mathbf {a} _ {2}\ cdot\ mathbf {e} _ {1} -\ dfrac {\ mathbf {a} _ {2}\ cdot\ mathbf {e} _ {1}} {e_ {1} ^ {2}}}\ mathbf {e} _ {1}\ cdot\ mathbf {e} _ {1}\\
&=\ mathbf {a} _ {2}\ cdot\ mathbf {e} _ {1} -\ mathbf {a} _ {2}\ cdot\ mathbf {e} _ {1} =0
\ end {alineado}\ etiqueta {7.4}\]

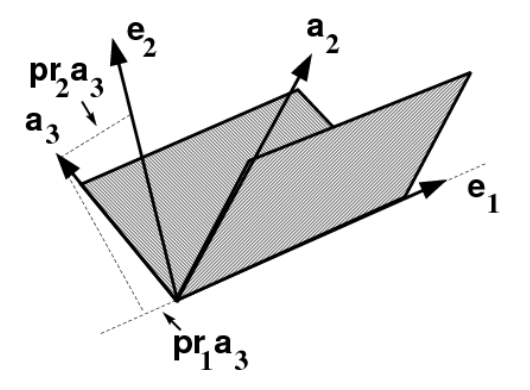
Ahora, buscamos un tercer vector\(\mathbf{e}_{3}\) que sea ortogonal a ambos\(\mathbf{e}_{1}\) y\(\mathbf{e}_{2}\). Pictorialmente, podemos escribir el vector dado\(\mathbf{a}_{3}\) como una combinación de proyecciones vectoriales a lo largo\(\mathbf{e}_{1}\) y\(\mathbf{e}_{2}\) y el nuevo vector. Esto se muestra en la Figura 7.3. Entonces tenemos,

\[\mathbf{e}_{3}=\mathbf{a}_{3}-\dfrac{\mathbf{a}_{3} \cdot \mathbf{e}_{1}}{e_{1}^{2}} \mathbf{e}_{1}-\dfrac{\mathbf{a}_{3} \cdot \mathbf{e}_{2}}{e_{2}^{2}} \mathbf{e}_{2} . \label{7.5} \]

Nuevamente, es una cuestión sencilla calcular los productos escalares con\(\mathbf{e}_{1}\) y\(\mathbf{e}_{2}\) verificar la ortogonalidad.

Podemos generalizar fácilmente el procedimiento al caso\(N\) -dimensional.

Organización Gram-Schmidt en\(N\)-Dimensions

Let\(\mathbf{a}_{n}, n=1, \ldots, N\) Ser un conjunto de vectores linealmente independientes en\(\mathbf{R}^{N}\). Entonces, se puede encontrar una base ortogonal estableciendo\(\mathbf{e}_{1}=\mathbf{a}_{1}\) y para\(n>1\),

\[\mathbf{e}_{n}=\mathbf{a}_{n}-\sum_{j=1}^{n-1} \dfrac{\mathbf{a}_{n} \cdot \mathbf{e}_{j}}{e_{j}^{2}} \mathbf{e}_{j} \label{7.6} \]

Figura 7.3. Una gráfica de los vectores y sus proyecciones para determinar\(e_3\).

Ahora, podemos generalizar esta idea a espacios funcionales (reales).

Ortogonalización Gram-Schmidt para Espacios Funcionales

Let\(f_{n}(x), n \in N_{0}=\{0,1,2, \ldots\}\), ser una secuencia linealmente independiente de funciones continuas definidas para\(x \in[a, b]\). Entonces, una base ortogonal de funciones, se\(\phi_{n}(x), n \in N_{0}\) puede encontrar y es dada por

\[\phi_{0}(x)=f_{0}(x) \nonumber \]

y

\[\phi_{n}(x)=f_{n}(x)-\sum_{j=0}^{n-1} \dfrac{<f_{n}, \phi_{j}>}{\left\|\phi_{j}\right\|^{2}} \phi_{j}(x), \quad n=1,2, \ldots \label{7.7} \]

Aquí estamos utilizando productos internos relativos al peso\(\sigma(x)\),

\[<f, g>=\int_{a}^{b} f(x) g(x) \sigma(x) d x \label{7.8} \]

Observe la similitud entre la base ortogonal en (7.7) y la expresión para el caso dimensional finito en la Ecuación (7.6).

Ejemplo 7.1. Aplicar el proceso de ortogonalización Gram-Schmidt al conjunto\(f_n(x) = x^n, n \in N_0\), when \(x \in (-1, 1)\) and \(\sigma(x) = 1\).

Primero, tenemos\(\phi_{0}(x)=f_{0}(x)=1\). Tenga en cuenta que

\[\int_{-1}^{1} \phi_{0}^{2}(x) d x=\dfrac{1}{2}. \nonumber \]

Podríamos usar este resultado para fijar la normalización de nuestra nueva base, pero vamos a dejar de hacerlo por ahora.

Ahora, calculamos el segundo elemento base:

\ [\ begin {alineado}
\ phi_ {1} (x) &=f_ {1} (x) -\ dfrac {<f_ {1},\ phi_ {0} >} {} {\ izquierda\ |\ phi_ {0}\ derecha\ |^ {2}}\ phi_ {0} (x)\\
&=x-\ dfrac {<x, 1>} {\ |1\ |^ {2}} 1=x
\ end {alineado}\ etiqueta {7.9}\]

ya que\(<x, 1>\) es la integral de una función impar sobre un intervalo simétrico.

Para\(\phi_{2}(x)\), tenemos

\ [\ begin {alineado}
\ phi_ {2} (x) &=f_ {2} (x) -\ dfrac {<f_ {2},\ phi_ {0} >} {\ izquierda\ |\ phi_ {0}\ derecha\ |^ {2}}\ phi_ {0} (x) -\ dfrac {<f_ {2},\ phi_ {1} >} {\ izquierda\ |\ phi_ {1}\ derecha\ |^ {2}}\ phi_ {1}} (x)\\
&=x^ {2} -\ dfrac {<x^ {2}, 1>} {\ |1\ |^ {2}} 1-\ dfrac {\ izquierda\ langle x^ {2}, x>\ derecha.} {\ |x\ |^ {2}} x\\
&=x^ {2} -\ dfrac {\ int_ {-1} ^ {1} x^ {2} d x} {\ int_ {-1} ^ {1} d x}\\
&=x^ {2} -\ dfrac {1} {3}.
\ end {alineado}\ etiqueta {7.10}\]

Hasta el momento, tenemos el conjunto ortogonal\(\left\{1, x, x^{2}-\dfrac{1}{3}\right\}\). Si uno elige normalizar estos forzando\(\phi_{n}(1)=1\), entonces se obtienen los polinomios clásicos de Legendre,\(P_{n}(x)=\phi_{1}(x)\). Así,

\[P_{2}(x)=\dfrac{1}{2}\left(3 x^{2}-1\right) . \nonumber \]

Tenga en cuenta que esta normalización es diferente a la habitual. De hecho, vemos que\(P_{2}(x)\) no tiene norma unitaria,

\[\left\|P_{2}\right\|^{2}=\int_{-1}^{1} P_{2}^{2}(x) d x=\dfrac{2}{5} . \nonumber \]

El conjunto de polinomios de Legendre es solo un conjunto de polinomios ortogonales clásicos que se pueden obtener de esta manera. Muchos habían aparecido originalmente como soluciones de importantes problemas de valor límite en la física. Todos ellos tienen propiedades similares y solo elaboraremos algunas de estas para las funciones de Legendre en la siguiente sección. Otros polinomios ortogonales de este grupo se muestran en la Tabla 7.1.

Como referencia, también observamos las ecuaciones diferenciales satisfechas por estas funciones.