7.2: Polinomios de Legendre
- Page ID
- 118902
En la última sección vimos los polinomios de Legendre en el contexto de bases ortogonales para un conjunto de funciones integrables cuadradas en\(L^{2}(-1,1)\). En tu primer curso en ecuaciones diferenciales, viste estos polinomios como una de las soluciones de la ecuación diferencial
\ (\ begin {array} {c|c|c|c}
\ text {polinomio} &\ text {Símbolo} &\ text {Intervalo} &\ sigma (x)\
\\ hline\ texto {Hermite} & H_ {n} (x) & (-\ infty,\ infty) & e^ {-x^ {2}}\
\ texto {Laguerre} & L_ {n} ^ {\ alpha} (x) & {[0,\ infty)} & e^ { -x}\\
\ texto {Legendre} & P_ {n} (x) & (-1,1) & 1\\
\ texto {Gegenbauer} & C_ {n} ^ {\ lambda} (x) & (-1,1) &\ izquierda (1-x^ {2}\ derecha) ^ {\ lambda-1/2}\
\ texto {Tchebychef de 1er tipo} & Tchebychef de primer tipo} & T_ {n} (x) & (-1,1) & Tchebychef de 1ª clase} & T_ _ {n} (x) & (-1,1) &\ izquierda (1-x^ {2}\ derecha) ^ {-1/2 }\\
\ text {Tchebychef del 2do tipo} & U_ {n} (x) & (-1,1) &\ izquierda (1-x^ {2}\ derecha) ^ {-1/2}\
\ texto {Jacobi} & P_ {n} ^ {(\ nu,\ mu)} (x) & (-1,1) & (1-x) ^ {\ nu} (1-x) ^ {\ mu}
\ end {array}\)
Cuadro 7.1. Polinomios ortogonales clásicos comunes con la función de intervalo y peso utilizada para definirlos.
\ (\ begin {array} {c|c}
\ text {polinomio} &\ text {Ecuación Diferencial}\\ hline
\ text {Hermite} & y^ {\ prime\ prime} -2 x y^ {\ prime} +2 n y=0\\ texto {Laguerre} & x y^ {
\ prime\ prime} + (\ alpha+1-x) y^ {prime\} + (\ alpha+1-x) y^ {prime\} n y=0\
\\ texto {Legendre} &\ izquierda (1-x^ {2}\ derecha) y^ {\ prime\ prime} -2 x y^ {\ prime} +n (n+1) y=0\\
\ texto {Gegenbauer} &\ izquierda (1-x^ {2}\ derecha) y^ {\ prime\ prime} - (2 n+3) x y^ {\ prime} +\ lambda y=0\
& izquierda\ (1-x^ {2}\ derecha) y^ {\ prime\ prime} -x y^ {\ prime} +n^ {2} y=0\\
\ texto {Tchebychef de el 1er tipo} &\ izquierda (1-x^ {2}\ derecha) y^ {\ prime\ prime} + (\ nu-\ mu+ (\ mu+\ nu+2) x) y^ {\ prime} +n (n+1+\ mu+\ nu) y=0\\
\ text {Jacobi} &\ mu+ (n+1+2)
\ end {array}\)
Cuadro 7.2. Ecuaciones diferenciales satisfechas por algunos de los polinomios ortogonales clásicos comunes.
\[\left(1-x^{2}\right) y^{\prime \prime}-2 x y^{\prime}+n(n+1) y=0, \quad n \in N_{0} . \label{7.11} \]
Recordemos que estos se obtuvieron mediante el uso de métodos de expansión en serie de potencia. En esta sección exploraremos algunas de las propiedades de estas funciones.
Para completarlo, recordamos la solución de la Ecuación (7.11) utilizando el método de series de potencia. Suponemos que la solución toma la forma
\[y(x)=\sum_{k=0}^{\infty} a_{k} x^{k} \nonumber \]
El objetivo es determinar los coeficientes,\(a_{k}\). Insertando esta serie en la Ecuación (7.11), tenemos
\[\left(1-x^{2}\right) \sum_{k=0}^{\infty} k(k-1) a_{k} x^{k-2}-\sum_{k=0}^{\infty} 2 a_{k} k x^{k}+\sum_{k=0}^{\infty} n(n+1) a_{k} x^{k}=0 \nonumber \]
o
\[\sum_{k=2}^{\infty} k(k-1) a_{k} x^{k-2}-\sum_{k=2}^{\infty} k(k-1) a_{k} x^{k}+\sum_{k=0}^{\infty}[-2 k+n(n+1)] a_{k} x^{k}=0 \nonumber \]
Podemos combinar algunos de estos términos:
\[\sum_{k=2}^{\infty} k(k-1) a_{k} x^{k-2}+\sum_{k=0}^{\infty}[-k(k-1)-2 k+n(n+1)] a_{k} x^{k}=0. \nonumber \]
Mayores rendimientos de simplificación
\[\sum_{k=2}^{\infty} k(k-1) a_{k} x^{k-2}+\sum_{k=0}^{\infty}[n(n+1)-k(k+1)] a_{k} x^{k}=0 \nonumber \]
Tenemos que recoger como poderes de\(x\). Esto se puede hacer reindexando cada suma. En la primera suma, dejamos\(m=k-2\), o\(k=m+2\). En la segunda suma dejamos de forma independiente\(k=m\). Entonces todos los poderes de\(x\) son de la forma\(x^{m}\). Esto da
\[\sum_{m=0}^{\infty}(m+2)(m+1) a_{m+2} x^{m}+\sum_{m=0}^{\infty}[n(n+1)-m(m+1)] a_{m} x^{m}=0 . \nonumber \]
Combinando estas sumas, tenemos
\[\sum_{m=0}^{\infty}\left[(m+2)(m+1) a_{m+2}+(n(n+1)-m(m+1)) a_{m}\right] x^{m}=0 . \nonumber \]
Esto tiene que aguantar para todos\(x\). Entonces, los coeficientes de\(x^{m}\) deben desaparecer:
\[(m+2)(m+1) a_{m+2}+(n(n+1)-m(m+1)) a_{m} . \nonumber \]
Resolviendo para\(a_{m+2}\), obtenemos la relación de recursión
\[a_{m+2}=\dfrac{n(n+1)-m(m+1)}{(m+2)(m+1)} a_{m}, \quad m \geq 0 . \nonumber \]
Así,\(a_{m+2}\) es proporcional a\(a_{m}\). Podemos iterar y mostrar que cada coeficiente es proporcional a\(a_{0}\) o\(a_{1}\). Sin embargo, para\(n\) un entero, tarde o temprano,\(m=n\) y la serie trunca. \(a_{m}=0\)para\(m>n\). Así, obtenemos soluciones polinomiales. Estas soluciones polinómicas son los polinomios de Legendre, que designamos como\(y(x)=P_{n}(x)\). Además, para\(n\) un entero par,\(P_{n}(x)\) es una función par y para\(n\) un entero impar,\(P_{n}(x)\) es una función impar.
En realidad, esta es una versión recortada del método. Habría que encontrar una segunda solución linealmente independiente. No discutiremos estas soluciones y dejaremos eso para que el lector interesado investigue.
7.2.1 La Fórmula Rodrigues
La primera propiedad que tienen los polinomios de Legendre es la fórmula Rodrigues:
\[P_{n}(x)=\dfrac{1}{2^{n} n !} \dfrac{d^{n}}{d x^{n}}\left(x^{2}-1\right)^{n}, \quad n \in N_{0} . \label{7.12} \]
A partir de la fórmula Rodrigues, se puede demostrar que\(P_{n}(x)\) es un polinomio de grado\(n\) th. También, para\(n\) impar, el polinomio es una función impar y para\(n\) par, el polinomio es una función par.
Como ejemplo, determinamos\(P_{2}(x)\) a partir de la fórmula de Rodrigues:
\ [\ begin {alineado}
P_ {2} (x) &=\ dfrac {1} {2^ {2} 2!} \ dfrac {d^ {2}} {d x^ {2}}\ izquierda (x^ {2} -1\ derecha) ^ {2}\\
&=\ dfrac {1} {8}\ dfrac {d^ {2}} {d x^ {2}}\ izquierda (x^ {4} -2 x^ {2} +1\ derecha)\\
&=\ dfrac {1} {8}\ dfrac {d} {d x}\ izquierda (4 x^ {3} -4 x\ derecha)\\
&=\ dfrac {1} {8}\ izquierda (12 x^ {2} -4\ derecha)\\
&=\ dfrac {1} {2}\ izquierda (3 x^ {2} -1\ derecha).
\ end {alineado}\ etiqueta {7.13}\]
Tenga en cuenta que obtenemos el mismo resultado que encontramos en la última sección usando ortogonalización.
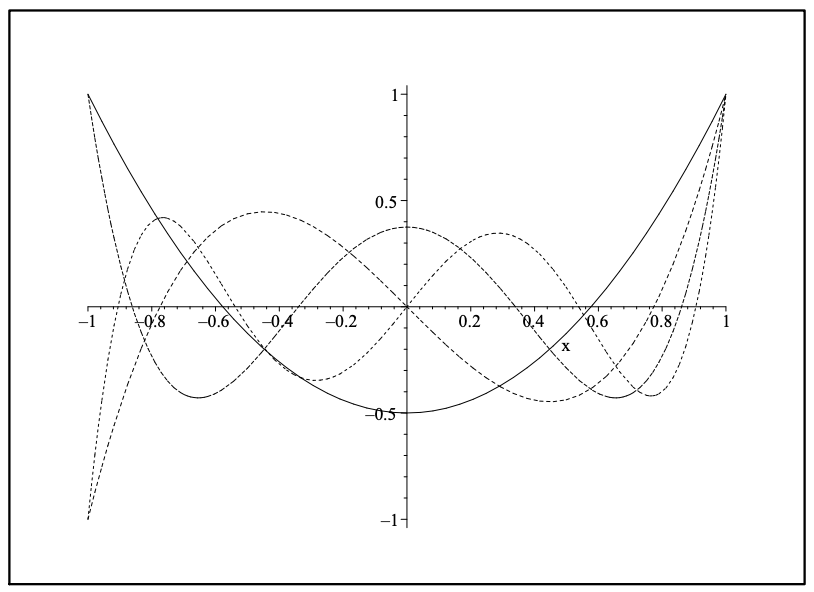
Se pueden generar sistemáticamente los polinomios de Legendre en forma tabular como se muestra en la Tabla 7.2.1. En la Figura 7.4 se muestran algunos polinomios de Legendre.
| \(n\) | \(\left(x^{2}-1\right)^{n}\) | \(\dfrac{d^{n}}{d x^{n}}\left(x^{2}-1\right)^{n}\) | \(\dfrac{1}{2 n_{n !}}\) | \(P_{n}(x)\) |
|---|---|---|---|---|
| \ (n\) ">0 | \ (\ izquierda (x^ {2} -1\ derecha) ^ {n}\) ">1 | \ (\ dfrac {d^ {n}} {d x^ {n}}\ izquierda (x^ {2} -1\ derecha) ^ {n}\) ">1 | \ (\ dfrac {1} {2 n_ {n!}} \) ">1 | \ (P_ {n} (x)\) ">1 |
| \ (n\) ">1 | \ (\ izquierda (x^ {2} -1\ derecha) ^ {n}\) ">\(x^{2}-1\) | \ (\ dfrac {d^ {n}} {d x^ {n}}\ izquierda (x^ {2} -1\ derecha) ^ {n}\) ">\(2x\) | \ (\ dfrac {1} {2 n_ {n!}} \) ">\(\dfrac{1}{2}\) | \ (P_ {n} (x)\) ">\(x\) |
| \ (n\) ">2 | \ (\ izquierda (x^ {2} -1\ derecha) ^ {n}\) ">\(x^{4}-2 x^{2}+1\) | \ (\ dfrac {d^ {n}} {d x^ {n}}\ izquierda (x^ {2} -1\ derecha) ^ {n}\) ">\(12 x^{2}-4\) | \ (\ dfrac {1} {2 n_ {n!}} \) ">\(\dfrac{1}{8}\) | \ (P_ {n} (x)\) ">\(\dfrac{1}{2}\left(3 x^{2}-1\right)\) |
| \ (n\) ">3 | \ (\ izquierda (x^ {2} -1\ derecha) ^ {n}\) ">\(x^{6}-3 x^{4}+3 x^{2}-1\) | \ (\ dfrac {d^ {n}} {d x^ {n}}\ izquierda (x^ {2} -1\ derecha) ^ {n}\) ">\(120 x^{3}-72 x\) | \ (\ dfrac {1} {2 n_ {n!}} \) ">\(\dfrac{1}{48}\) | \ (P_ {n} (x)\) ">\(\dfrac{1}{2}\left(5 x^{3}-3 x\right)\) |
Cuadro 7.3. Cálculo tabular de los polinomios de Legendre utilizando la fórmula Rodrigues.
7.2.2 Fórmula de recursión de tres períodos
Los polinomios ortogonales clásicos también satisfacen tres fórmulas de recurrencia de término. En el caso de los polinomios de Legendre, tenemos
\[(2 n+1) x P_{n}(x)=(n+1) P_{n+1}(x)+n P_{n-1}(x), \quad n=1,2, \ldots \label{7.14} \]
Esto también se puede reescribir reemplazando\(n\) con\(n-1\) como
\[(2 n-1) x P_{n-1}(x)=n P_{n}(x)+(n-1) P_{n-2}(x), \quad n=1,2, \ldots \label{7.15} \]
Demostraremos esta fórmula de recursividad de dos maneras. Primero utilizamos las propiedades de ortogonalidad de los polinomios de Legendre y el siguiente lema.
El coeficiente principal de\(x^{n}\) in\(P_{n}(x)\) es\(\dfrac{1}{2^{n} n !} \dfrac{(2 n) !}{n !}\).
Prueba. Podemos demostrarlo usando la fórmula Rodrigues. primero, nos enfocamos en el coeficiente principal de\(\left(x^{2}-1\right)^{n}\), que es\(x^{2 n}\). La primera derivada de\(x^{2 n}\) es\(2 n x^{2 n-1}\). La segunda derivada es\(2 n(2 n-1) x^{2 n-2}\). El\(j\) th derivado es
\[\dfrac{d^{j} x^{2 n}}{d x^{j}}=[2 n(2 n-1) \ldots(2 n-j+1)] x^{2 n-j} \nonumber \]
Así, la derivada\(n\) th viene dada por
\[\dfrac{d^{n} x^{2 n}}{d x^{n}}=[2 n(2 n-1) \ldots(n+1)] x^{n} \nonumber \]
Esto prueba que\(P_{n}(x)\) tiene grado\(n\). El coeficiente principal de ahora se\(P_{n}(x)\) puede escribir como
\ [\ comenzar {alineado}
\ dfrac {1} {2^ {n} n!} [2 n (2 n-1)\ lpuntos (n+1)] &=\ dfrac {1} {2^ {n} n!} [2 n (2 n-1)\ lpuntos (n+1)]\ dfrac {n (n-1)\ lpuntos 1} {n (n-1)\ lpuntos 1}\\\
&=\ dfrac {1} {2^ {n} n!} \ dfrac {(2 n)!} {n!} .
\ end {alineado}\ etiqueta {7.16}\]
Para probar la fórmula de recursión de tres términos consideramos la expresión\((2 n-1) x P_{n-1}(x)-n P_{n}(x)\). Si bien cada término es un polinomio de grado\(n\), los términos de orden principal cancelan. Solo necesitamos mirar el coeficiente de la primera expresión del término de orden principal. Es
\[(2 n-1) \dfrac{1}{2^{n-1}(n-1) !} \dfrac{(2 n-2) !}{(n-1) !}=\dfrac{1}{2^{n-1}(n-1) !} \dfrac{(2 n-1) !}{(n-1) !}=\dfrac{(2 n-1) !}{2^{n-1}[(n-1) !]^{2}} . \nonumber \]
El coeficiente del término principal para se\(n P_{n}(x)\) puede escribir como
\[n \dfrac{1}{2^{n} n !} \dfrac{(2 n) !}{n !}=n\left(\dfrac{2 n}{2 n^{2}}\right)\left(\dfrac{1}{2^{n-1}(n-1) !}\right) \dfrac{(2 n-1) !}{(n-1) !} \dfrac{(2 n-1) !}{2^{n-1}[(n-1) !]^{2}} . \nonumber \]
Es fácil ver que los términos de pedido líder en\((2 n-1) x P_{n-1}(x)-n P_{n}(x)\) cancelar.
Los siguientes términos serán de grado\(n-2\). Esto se debe a que los\(P_{n}\)'s son funciones pares o impares, por lo tanto, solo contienen pares, o impares, poderes de\(x\). Concluimos que
\[(2 n-1) x P_{n-1}(x)-n P_{n}(x)=\text { polynomial of degree } n-2 . \nonumber \]
Por lo tanto, dado que los polinomios de Legendre forman una base, podemos escribir este polinomio como una combinación lineal de polinomios de Legendre:
\[(2 n-1) x P_{n-1}(x)-n P_{n}(x)=c_{0} P_{0}(x)+c_{1} P_{1}(x)+\ldots+c_{n-2} P_{n-2}(x) . \label{7.17} \]
Multiplicando la Ecuación (7.17) por\(P_{m}(x)\) for\(m=0,1, \ldots, n-3\), integrando de -1 a 1, y usando ortogonalidad, obtenemos
\[0=c_{m}\left\|P_{m}\right\|^{2}, \quad m=0,1, \ldots, n-3 . \nonumber \]
[Nota:\(\int_{-1}^{1} x^{k} P_{n}(x) d x=0\) para\(k \leq n-1\). Así,\(\int_{-1}^{1} x P_{n-1}(x) P_{m}(x) d x=0\) para\(m \leq n-3 .]\)
Así, todos estos\(c_{m}\) son cero, dejando la Ecuación (7.17) como
\[(2 n-1) x P_{n-1}(x)-n P_{n}(x)=c_{n-2} P_{n-2}(x) . \nonumber \]
El coeficiente final se puede encontrar usando la condición de normalización,\(P_{n}(1)=1\). Así,\(c_{n-2}=(2 n-1)-n=n-1\).
7.2.3 La Función Generadora
Se puede obtener una segunda prueba de la fórmula de recursión de tres términos a partir de la función generadora de los polinomios de Legendre. Muchas funciones especiales tienen tales funciones generadoras. En este caso viene dado por
\[g(x, t)=\dfrac{1}{\sqrt{1-2 x t+t^{2}}}=\sum_{n=0}^{\infty} P_{n}(x) t^{n}, \quad|x|<1,|t|<1 \label{7.18} \]
Esta función generadora ocurre a menudo en aplicaciones. En particular, surge en la teoría del potencial, como los potenciales electromagnéticos o gravitacionales. Estas funciones potenciales son funciones\(\dfrac{1}{r}\) de tipo. Por ejemplo, el potencial gravitacional entre la Tierra y la luna es proporcional al recíproco de la magnitud de la diferencia entre sus posiciones respecto a algún sistema de coordenadas. Un ejemplo aún mejor, sería colocar el origen en el centro de la Tierra y considerar las fuerzas sobre la Tierra no puntual debido a la luna. Considera un pedazo de la Tierra en posición\(\mathbf{r}_{1}\) y la luna en posición\(\mathbf{r}_{2}\) como se muestra en la Figura 7.5. El potencial de marea\(\Phi\) es proporcional a
\[\Phi \propto \dfrac{1}{\left|\mathbf{r}_{2}-\mathbf{r}_{1}\right|}=\dfrac{1}{\sqrt{\left(\mathbf{r}_{2}-\mathbf{r}_{1}\right) \cdot\left(\mathbf{r}_{2}-\mathbf{r}_{1}\right)}}=\dfrac{1}{\sqrt{r_{1}^{2}-2 r_{1} r_{2} \cos \theta+r_{2}^{2}}}, \nonumber \]
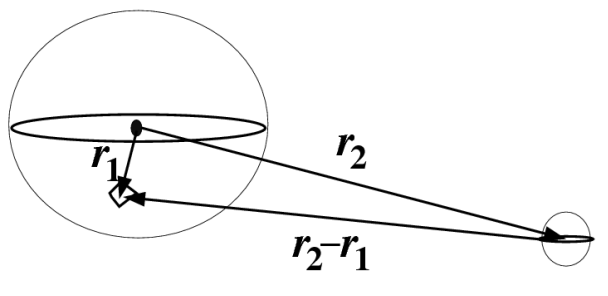
donde\(\theta\) esta el angulo entre\(\mathbf{r}_{1}\) y\(\mathbf{r}_{2}\).
Típicamente, uno de los vectores de posición es mucho más grande que el otro. Supongamos eso\(r_{1} \ll r_{2}\). Entonces, uno puede escribir
\[\Phi \propto \dfrac{1}{\sqrt{r_{1}^{2}-2 r_{1} r_{2} \cos \theta+r_{2}^{2}}}=\dfrac{1}{r_{2}} \dfrac{1}{\sqrt{1-2 \dfrac{r_{1}}{r_{2}} \cos \theta+\left(\dfrac{r_{1}}{r_{2}}\right)^{2}}} \nonumber \]
Ahora, definir\(x=\cos \theta\) y\(t=\dfrac{r_{1}}{r_{2}}\). Entonces tenemos el potencial de marea es proporcional a la función generadora para los polinomios de Legendre! Entonces, podemos escribir el potencial mareante como
\[\Phi \propto \dfrac{1}{r_{2}} \sum_{n=0}^{\infty} P_{n}(\cos \theta)\left(\dfrac{r_{1}}{r_{2}}\right)^{n}. \nonumber \]
El primer término en la expansión es el potencial gravitacional que da la fuerza habitual entre la Tierra y la Luna. [Recordemos que la fuerza es el gradiente del potencial,\(\mathbf{F}=\nabla\left(\dfrac{1}{r}\right)\).] Los siguientes términos darán expresiones para los efectos mareales.
Ahora que tenemos alguna idea de dónde podría haberse originado esta función generadora, podemos proceder a usarla. En primer lugar, la función generadora puede ser utilizada para obtener valores especiales de los polinomios de Legendre.
\[g(0, t)=\dfrac{1}{\sqrt{1+t^{2}}}=\sum_{n=0}^{\infty} P_{n}(0) t^{n} . \label{7.19} \]
Podemos usar la expansión binomial para encontrar nuestra respuesta final. [Ver la última sección de este capítulo para una revisión.] A saber, tenemos
\[\dfrac{1}{\sqrt{1+t^{2}}}=1-\dfrac{1}{2} t^{2}+\dfrac{3}{8} t^{4}+\ldots \nonumber \]
Comparando estas expansiones, tenemos el\(P_{n}(0)=0\) para los enteros\(n\) impares y pares se puede mostrar (ver Problema 7.10) que
\[P_{2 n}(0)=(-1)^{n} \dfrac{(2 n-1) ! !}{(2 n) ! !}, \label{7.20} \]
donde\(n!!\) está el doble factorial,
\ (n! ! =\ left\ {\ begin {array} {cc}
n (n-2)\ ldots (3) 1, & n>0,\ text {impar}\\
n (n-2)\ ldots (4) 2, & n>0,\ text {par}. \\
1 & n=0, -1
\ end {array}\ right.\)
\[g(-1, t)=\dfrac{1}{\sqrt{1+2 t+t^{2}}}=\dfrac{1}{1+t}=1-t+t^{2}-t^{3}+\ldots \nonumber \]
Por lo tanto,\(P_{n}(-1)=(-1)^{n}\).
También podemos usar la función generadora para encontrar relaciones de recursión. Para probar la recursión de tres términos (7.14) que introdujimos anteriormente, entonces sólo necesitamos diferenciar la función generadora con respecto a\(t\) en la Ecuación (7.18) y reorganizar el resultado. Primero tenga en cuenta que
\[\dfrac{\partial g}{\partial t}=\dfrac{x-t}{\left(1-2 x t+t^{2}\right)^{3 / 2}}=\dfrac{x-t}{1-2 x t+t^{2}} g(x, t) \nonumber \]
Combinando esto con
\[\dfrac{\partial g}{\partial t}=\sum_{n=0}^{\infty} n P_{n}(x) t^{n-1} \nonumber \]
tenemos
\[(x-t) g(x, t)=\left(1-2 x t+t^{2}\right) \sum_{n=0}^{\infty} n P_{n}(x) t^{n-1} . \nonumber \]
Insertando la expresión de serie para\(g(x, t)\) y distribuyendo la suma en el lado derecho, obtenemos
\[(x-t) \sum_{n=0}^{\infty} P_{n}(x) t^{n}=\sum_{n=0}^{\infty} n P_{n}(x) t^{n-1}-\sum_{n=0}^{\infty} 2 n x P_{n}(x) t^{n}+\sum_{n=0}^{\infty} n P_{n}(x) t^{n+1} . \nonumber \]
Reorganizar conduce a tres sumas separadas:
\[\sum_{n=0}^{\infty} n P_{n}(x) t^{n-1}-\sum_{n=0}^{\infty}(2 n+1) x P_{n}(x) t^{n}+\sum_{n=0}^{\infty}(n+1) P_{n}(x) t^{n+1}=0 \label{7.21} \]
Cada término contiene poderes de los\(t\) que nos gustaría combinar en una sola suma. Esto se hace mediante la reindexación. Para la primera suma, podríamos usar el nuevo índice\(k=n-1\). Entonces, se puede escribir la primera suma
\[\sum_{n=0}^{\infty} n P_{n}(x) t^{n-1}=\sum_{k=-1}^{\infty}(k+1) P_{k+1}(x) t^{k} \nonumber \]
Usar diferentes índices es solo otra forma de escribir los términos. Tenga en cuenta que
\[\sum_{n=0}^{\infty} n P_{n}(x) t^{n-1}=0+P_{1}(x)+2 P_{2}(x) t+3 P_{3}(x) t^{2}+\ldots \nonumber \]
y
\[\sum_{k=-1}^{\infty}(k+1) P_{k+1}(x) t^{k}=0+P_{1}(x)+2 P_{2}(x) t+3 P_{3}(x) t^{2}+\ldots \nonumber \]
en realidad dan la misma suma. A los índices se les hace referencia a veces como índices ficticio porque no aparecen en la expresión expandida y pueden ser reemplazados por otra letra.
Si queremos hacerlo, ahora podríamos reemplazar todos los's por\(k\)'s Sin embargo, dejaremos los\(n\)\(k\)'s en el primer término y ahora reindexaremos las siguientes sumas en la Ecuación (7.21). La segunda suma solo necesita el reemplazo\(n=k\) y la última suma que reindexamos usando\(k=n+1\). Por lo tanto, la ecuación (7.21) se convierte en
\[\sum_{k=-1}^{\infty}(k+1) P_{k+1}(x) t^{k}-\sum_{k=0}^{\infty}(2 k+1) x P_{k}(x) t^{k}+\sum_{k=1}^{\infty} k P_{k-1}(x) t^{k}=0 \label{7.22} \]
Ahora podemos combinar todos los términos, señalando que el\(k=-1\) término es automáticamente cero y los\(k=0\) términos dan
\[P_{1}(x)-x P_{0}(x)=0 . \label{7.23} \]
Por supuesto, ya lo sabemos. Entonces, eso deja los\(k>0\) términos:
\[\sum_{k=1}^{\infty}\left[(k+1) P_{k+1}(x)-(2 k+1) x P_{k}(x)+k P_{k-1}(x)\right] t^{k}=0 \label{7.24} \]
Como esto es cierto para todos\(t\), los coeficientes de los\(t^{k}\)'s son cero, o
\[(k+1) P_{k+1}(x)-(2 k+1) x P_{k}(x)+k P_{k-1}(x)=0, \quad k=1,2, \ldots \nonumber \]
Hay otras relaciones de recursión. Por ejemplo,
\[P_{n+1}^{\prime}(x)-P_{n-1}^{\prime}(x)=(2 n+1) P_{n}(x) . \label{7.25} \]
Esto se puede probar utilizando la función generadora diferenciando\(g(x, t)\) con respecto\(x\) y reordenando las series infinitas resultantes al igual que en esta última manipulación. Esto quedará como Problema 7.4.
Otro uso de la función generadora es obtener la constante de normalización. A saber,\(\left\|P_{n}\right\|^{2}\). Al cuadrar la función generadora, tenemos
\[\dfrac{1}{1-2 x t+t^{2}}=\left[\sum_{n=0}^{\infty} P_{n}(x) t^{n}\right]^{2}=\sum_{n=0}^{\infty} \sum_{m=0}^{\infty} P_{n}(x) P_{m}(x) t^{n+m} \label{7.26} \]
Integrando de -1 a 1 y usando la ortogonalidad de los polinomios de Legendre, tenemos
\ [\ begin {alineado}
\ int_ {-1} ^ {1}\ dfrac {d x} {1-2 x t+t^ {2}} &=\ sum_ {n=0} ^ {\ infty}\ suma_ {m=0} ^ {\ infty} t^ {n+m}\ int_ {-1} ^ {1} P_ {n} (x) P_ {m} (x) d x\\
&=\ sum_ {n=0} ^ {\ infty} t^ {2 n}\ int_ {-1} ^ {1} P_ {n} ^ {2} (x) d x
\ final {alineado}\ etiqueta {7.27}\]
Sin embargo, se puede demostrar que
\[\int_{-1}^{1} \dfrac{d x}{1-2 x t+t^{2}}=\dfrac{1}{t} \ln \left(\dfrac{1+t}{1-t}\right) . \nonumber \]
Ampliando esta expresión sobre\(t=0\), obtenemos
\[\dfrac{1}{t} \ln \left(\dfrac{1+t}{1-t}\right)=\sum_{n=0}^{\infty} \dfrac{2}{2 n+1} t^{2 n} \nonumber \]
Comparando este resultado con la Ecuación (7.27), encontramos que
\[\left\|P_{n}\right\|^{2}=\int_{-1}^{1} P_{n}(x) P_{m}(x) d x=\dfrac{2}{2 n+1} . \label{7.28} \]
7.2.4 Expansiones de función propia
Finalmente, podemos expandir otras funciones en esta base ortogonal. Esto es solo una serie generalizada de Fourier. Una expansión de la serie Fourier-Legendre para\(f(x)\) on\([-1,1]\) toma la forma
\[f(x) \sim \sum_{n=0}^{\infty} c_{n} P_{n}(x) . \label{7.29} \]
Como antes, podemos determinar los coeficientes multiplicando ambos lados por\(P_{m}(x)\) e integrándolos. La ortogonalidad da la forma habitual para los coeficientes generalizados de Fourier. En este caso, tenemos
\[c_{n}=\dfrac{<f, P_{n}>}{\left\|P_{n}\right\|^{2}}, \nonumber \]
donde
\[<f, P_{n}>=\int_{-1}^{1} f(x) P_{n}(x) d x . \nonumber \]
Acabamos de encontrar\(\left\|P_{n}\right\|^{2}=\dfrac{2}{2 n+1}\). Por lo tanto, los coeficientes de Fourier-Legendre son
\[c_{n}=\dfrac{2 n+1}{2} \int_{-1}^{1} f(x) P_{n}(x) d x . \label{7.30} \]
Simplemente necesitamos calcular
\[c_{n}=\dfrac{2 n+1}{2} \int_{-1}^{1} x^{3} P_{n}(x) d x \label{7.31} \]
Primero notamos que
\[\int_{-1}^{1} x^{m} P_{n}(x) d x=0 \quad \text { for } m<n . \nonumber \]
Esto simplemente se prueba usando la fórmula de Rodrigues. Insertando la ecuación (7.12), tenemos
\[\int_{-1}^{1} x^{m} P_{n}(x) d x=\dfrac{1}{2^{n} n !} \int_{-1}^{1} x^{m} \dfrac{d^{n}}{d x^{n}}\left(x^{2}-1\right)^{n} d x . \nonumber \]
Ya que\(m<n\), podemos integrar por partes $m$-veces para mostrar el resultado, usando\(P_{n}(1)=1\) y\(P_{n}(-1)=(-1)^{n}\). En consecuencia, tendremos para este ejemplo que\(c_{n}=0\) para\(n>3\).
Podríamos simplemente calcular\(\int_{-1}^{1} x^{3} P_{m}(x) d x\)\(m=0,1,2, \ldots\) por completo. Pero, al señalar que\(x^{3}\) es una función extraña, fácilmente confirmamos que\(c_{0}=0\) y\(c_{2}=0\). Esto nos deja con sólo dos coeficientes para calcular. Estos son
\[c_{1}=\dfrac{3}{2} \int_{-1}^{1} x^{4} d x=\dfrac{3}{5} \nonumber \]
y
\[c_{3}=\dfrac{7}{2} \int_{-1}^{1} x^{3}\left[\dfrac{1}{2}\left(5 x^{3}-3 x\right)\right] d x=\dfrac{2}{5} \nonumber \]
Por lo tanto,
\[x^{3}=\dfrac{3}{5} P_{1}(x)+\dfrac{2}{5} P_{3}(x) . \nonumber \]
Por supuesto, esto es sencillo de verificar usando la Tabla 7.2.1:
\[\dfrac{3}{5} P_{1}(x)+\dfrac{2}{5} P_{3}(x)=\dfrac{3}{5} x+\dfrac{2}{5}\left[\dfrac{1}{2}\left(5 x^{3}-3 x\right)\right]=x^{3} . \nonumber \]
Bueno, a lo mejor podríamos haber adivinado esto sin hacer ninguna integración. Vamos a ver,
\ [\ begin {alineado}
x^ {3} &=c_ {1} x+\ dfrac {1} {2} c_ {2}\ izquierda (5 x^ {3} -3 x\ derecha)\\
&=\ izquierda (c_ {1} -\ dfrac {3} {2} c_ {2}\ derecha) x+\ dfrac {5} {2} _ {2} x^ {3}.
\ end {alineado}\ etiqueta {7.32}\]
Equiparando coeficientes de términos similares, tenemos eso\(c_{2}=\dfrac{2}{5}\) y\(c_{1}=\dfrac{3}{2} c_{2}=\dfrac{3}{5}\).
La función Heaviside se define como
\ [H (x) =\ left\ {\ begin {array} {l}
1, x>0\\
0, x<0
\ end {array}\ right. \ label {7.33}\]
En este caso, no podemos encontrar los coeficientes de expansión sin alguna integración. Tenemos que computar
\ [\ begin {alineado}
c_ {n} &=\ dfrac {2 n+1} {2}\ int_ {-1} ^ {1} f (x) P_ {n} (x) d x\
&=\ dfrac {2 n+1} {2}\ int_ {0} ^ {1} P_ {n} (x) d x,\ quad n=0,1,2,\ ldots
\ end {alineado}\ etiqueta {7.34}\]
Para\(n=0\), tenemos
\[c_{0}=\dfrac{1}{2} \int_{0}^{1} d x=\dfrac{1}{2} . \nonumber \]
Para\(n>1\), hacemos uso de la identidad (7.25) para encontrar
\[c_{n}=\dfrac{1}{2} \int_{0}^{1}\left[P_{n+1}^{\prime}(x)-P_{n-1}^{\prime}(x)\right] d x=\dfrac{1}{2}\left[P_{n-1}(0)-P_{n+1}(0)\right] . \nonumber \]
Así, la serie Fourier-Bessel para la función Heaviside es
\[f(x) \sim \dfrac{1}{2}+\dfrac{1}{2} \sum_{n=1}^{\infty}\left[P_{n-1}(0)-P_{n+1}(0)\right] P_{n}(x) . \nonumber \]
Tenemos que evaluar\(P_{n-1}(0)-P_{n+1}(0)\). Ya que\(P_{n}(0)=0\) para\(n\) impar, los\(c_{n}\)'s desaparecen para\(n\) par. Dejando\(n=2 k-1\), tenemos
\[f(x) \sim \dfrac{1}{2}+\dfrac{1}{2} \sum_{k=1}^{\infty}\left[P_{2 k-2}(0)-P_{2 k}(0)\right] P_{2 k-1}(x) . \nonumber \]
Podemos usar la Ecuación (7.20),
\[P_{2 k}(0)=(-1)^{k} \dfrac{(2 k-1) ! !}{(2 k) ! !}, \nonumber \]
para calcular los coeficientes:
\ [\ begin {alineado}
f (x) &\ sim\ dfrac {1} {2} +\ dfrac {1} {2}\ sum_ {k=1} ^ {\ infty}\ izquierda [P_ {2 k-2} (0) -P_ {2 k} (0)\ derecha] P_ {2 k-1} (x)\\
&=\ dfrac {1} {2} +\ dfrac {1} {2}\ sum_ {k=1} ^ {\ infty}\ izquierda [(-1) ^ {k-1}\ dfrac {(2 k-3)! !} {(2 k-2)! !} - (-1) ^ {k}\ dfrac {(2 k-1)! !} {(2 k)! !} \ derecha] P_ {2 k-1} (x)\\
&=\ dfrac {1} {2} -\ dfrac {1} {2}\ sum_ {k=1} ^ {\ infty} (-1) ^ {k}\ dfrac {(2 k-3)! !} {(2 k-2)! !} \ izquierda [1+\ dfrac {2 k-1} {2 k}\ derecha] P_ {2 k-1} (x)\\
&=\ dfrac {1} {2} -\ dfrac {1} {2}\ sum_ {k=1} ^ {\ infty} (-1) ^ {k}\ dfrac {(2 k-3)! !} {(2 k-2)! !} \ dfrac {4 k-1} {2 k} P_ {2 k-1} (x).
\ end {alineado}\ etiqueta {7.35}\]
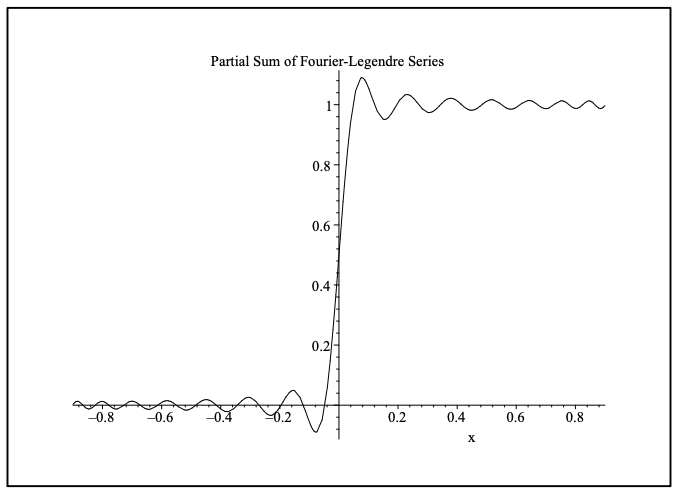
La suma de los primeros 21 términos se muestra en la Figura 7.6. Observamos la lenta convergencia a la función Heaviside. También, vemos que el fenómeno de Gibbs está presente debido a la discontinuidad del salto en\(x = 0\).