2.2: Mejores aproximaciones afín
- Page ID
- 111717
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)En esta sección generalizaremos las ideas básicas del cálculo diferencial de funciones\(f: \mathbb{R} \rightarrow \mathbb{R}\) a funciones\(f: \mathbb{R} \rightarrow \mathbb{R}^{n}\). Recordemos que dada una función\(f: \mathbb{R} \rightarrow \mathbb{R}\), decimos\(f\) es diferenciable en un punto\(c\) si existe una función afín\(A: \mathbb{R} \rightarrow \mathbb{R}\),\(A(x)=m(x-c)+f(c)\), tal que
\[ \lim _{h \rightarrow 0} \frac{f(c+h)-A(c+h)}{h}=0 . \label{2.2.1} \]
Llamamos a\(A\) la mejor aproximación afín a\(f\) at\(c\) y\(m\) la derivada de\(f\) at\(c\), denotada\(f^{\prime}(c)\). Además, llamamos a la gráfica de\(A\), es decir, la línea con ecuación
\[ y=f^{\prime}(c)(x-c)+f(c),\]
la línea tangente a la gráfica de\(f\) at\((c, f(c))\).
La condición (\(\ref{2.2.1}\)) dice que la función\(\varphi(h)=f(c+h)-A(c+h) \text { is } o(h)\). En general, decimos que una función\(\varphi: \mathbb{R} \rightarrow \mathbb{R}\) es\(o(h)\) si
\[ \lim _{h \rightarrow 0} \frac{\varphi(h)}{h}=0 .\]
Mejores aproximaciones afín
Generalizar la idea de la mejor aproximación afín al caso de una función\(f: \mathbb{R} \rightarrow \mathbb{R}^{n}\) requiere sólo una ligera modificación del requisito que\(f(c+h)-A(c+h)\) sea\(o(h)\). Es decir, dado que\(f(c+h)-A(c+h)\) es un vector en\(\mathbb{R}^{n}\), vamos a requerir que\(\|f(c+h)-A(c+h)\|\), en lugar de\(f(c+h)-A(c+h)\), ser\(o(h)\). Si\(n=1\), esto se reducirá a la definición de una variable ya que, en ese caso,\(\|f(c+h)-A(c+h)\|=|f(c+h)-A(c+h)|\) y una función\(\varphi: \mathbb{R} \rightarrow \mathbb{R}\) es\(o(h)\) si y sólo si\(|\varphi(h)|\) es\(o(h)\).
Definición\(\PageIndex{1}\)
Supongamos\(f: \mathbb{R} \rightarrow \mathbb{R}^{n}\) y\(c\) es un punto en el dominio de\(f\). Llamamos a una función afín\(A: \mathbb{R} \rightarrow \mathbb{R}^{n}\) la mejor aproximación afín a\(f\) at\(c\) if (1)\(A(c)=f(c)\) y (2)\(\|R(h)\|\) es\(o(h)\), donde
\[ R(h)=f(c+h)-A(c+h). \]
Supongamos\(f: \mathbb{R} \rightarrow \mathbb{R}^{n}\) y\(A: \mathbb{R} \rightarrow \mathbb{R}^{n}\) es una función afín para la cual\(A(c)=f(c)\). Ya que\(A\) es afín, existe una función lineal\(L: \mathbb{R} \rightarrow \mathbb{R}^{n}\) y un vector\(\mathbf{b}\) en\(\mathbb{R}^n\) tal que\(A(t)=L(t)+\mathbf{b}\) para todos\(t\) en\(\mathbb{R}\). Ya que tenemos
\[ f(c)=A(c)=L(c)+\mathbf{b},\]
de ello se deduce\(\mathbf{b}=f(c)-L(c)\). De ahí para todos\(t\) en\(\mathbb{R}\),
\[A(t)=L(t)+f(c)-L(c)=L(c-t)+f(c).\]
Además, si\(\mathbf{a}=L(1)\), entonces, de nuestros resultados en la Sección 1.5,
\[ A(t)=\mathbf{a}(t-c)+f(c).\]
De ahí
\[ R(h)=f(c+h)-A(c+h)=f(c+h)-f(c)-\mathbf{a} h , \]
de lo que se deduce que
\ [\ begin {align}
\ lim _ {h\ fila derecha 0^ {+}}\ frac {\ |R (h)\ |} {h} &=\ lim _ {h\ fila derecha 0^ {+}}\ frac {\ |f (c+h) -f (c) -\ mathbf {a} h\ |} {h}\ nonumber\
&=\ lim _ {h\ fila derecha 0^ {+}}\ izquierda\ |\ frac {f (c+h) -f (c) -\ mathbf {a} h} {h}\ derecha\ |\ etiqueta {}\\
&=\ lim _ {h\ fila derecha 0^ {+}}\ izquierda\ |\ frac {f (c+h) -f (c)} {h} -\ mathbf {a}\ derecha\ |\ nonumber
\ end {align}\]
Así
\[ \lim _{h \rightarrow 0^{+}} \frac{\|R(h)\|}{h}=0 \nonumber \]
si y solo si
\[ \lim _{h \rightarrow 0^{+}} \frac{f(c+h)-f(c)}{h}=\mathbf{a}. \nonumber \]
Un cálculo similar de la izquierda muestra que
\[\lim _{h \rightarrow 0^{-}} \frac{\|R(h)\|}{h}=0 \nonumber \]
si y solo si
\[ \lim _{h \rightarrow 0^{-}} \frac{f(c+h)-f(c)}{h}=\mathbf{a}.\nonumber \]
De ahí
\[ \lim _{h \rightarrow 0} \frac{\|R(h)\|}{h}=0\]
si y solo si
\[ \lim _{h \rightarrow 0} \frac{f(c+h)-f(c)}{h}=\mathbf{a}.\]
Es decir,\(A\) es la mejor aproximación afín a\(f\) en\(c\) si y sólo si, para todos\(t\) en\(\mathbb{R}\),
\[ A(t)=\mathbf{a}(t-c)+f(c), \]
donde
\[ \mathbf{a}=\lim _{h \rightarrow 0} \frac{f(c+h)-f(c)}{h}.\]
Definición\(\PageIndex{2}\)
Supongamos\(f: \mathbb{R} \rightarrow \mathbb{R}^{n}\). Si
\[ \lim _{h \rightarrow 0} \frac{f(c+h)-f(c)}{h}\]
existe, entonces decimos que\(f\) es diferenciable en\(c\) y llamamos
\[ D f(c)=\lim _{h \rightarrow 0} \frac{f(c+h)-f(c)}{h} \label{2.2.15} \]
la derivada de\(f\) at\(c\).
Tenga en cuenta que (\(\ref{2.2.15}\)) es lo mismo que la fórmula para la derivada en el cálculo de una variable. De hecho, en el caso\(n=1\), (\(\ref{2.2.15}\)) es solo la derivada del cálculo de una variable. No obstante\(n>1\), si, entonces\(D f(c)\) será un vector, no un escalar.
El siguiente teorema resume nuestro trabajo anterior.
Teorema\(\PageIndex{1}\)
Supongamos\(f: \mathbb{R} \rightarrow \mathbb{R}^{n}\) y\(c\) es un punto en el dominio de\(f\). Entonces\(f\) tiene una mejor aproximación afín\(A: \mathbb{R} \rightarrow \mathbb{R}^{n}\) en\(c\) si y solo si\(f\) es diferenciable en\(c\), en cuyo caso
\[ A(t)=D f(c)(t-c)+f(c) .\]
Vimos en la Sección 2.1 que un límite de una función de valor vectorial\(f\) puede calcularse evaluando el límite de cada función de coordenadas por separado. Este resultado tiene una consecuencia importante para los derivados informáticos. Supongamos que\(f: \mathbb{R} \rightarrow \mathbb{R}^{n}\) es diferenciable en\(c\). Si escribimos
\[ f(t)=\left(f_{1}(t), f_{2}(t), \ldots, f_{n}(t)\right. , \nonumber \]
entonces
\ [\ begin {alineado}
D f (c) &=\ lim _ {h\ fila derecha 0}\ frac {f (c+h) -f (c)} {h}\\
&=\ lim _ {h\ fila derecha 0}\ frac {1} {h}\ izquierda (\ izquierda (f_ {1} (c+h), f_ {2} (c+h),\ lpuntos, f_ {n} (c+h) -\ izquierda (f_ {1} (c), f_ {2} (c),\ ldots, f_ {n} (c)\ derecha)\ derecha. \ derecho. \\
&=\ lim _ {h\ fila derecha 0}\ izquierda (\ frac {f_ {1} (c+h) -f_ {1} (c)} {h},\ frac {f_ {2} (c+h) -f_ {2} (c)} {h},\ ldots,\ frac {f_ {n} (c+h) -f_ _ {n} (c)} {h}\ derecha)\\
&=\ izquierda (\ lim _ {h\ fila derecha 0}\ frac {f_ {1} (c+h) -f_ {1} (c)} {h},\ lim _ {h\ fila derecha 0}\ frac {f_ {2} (c+h) -f_ {2} (c)} {h},\ lpuntos,\ lim _ {h\ fila derecha 0}\ frac {f_ {n} (c+h) -f_ {n} (c)} {h}\ derecha)\\
&=\ izquierda (f_ {1} ^ {\ prime} (c), f_ {2} ^ {\ prime} (c),\ ldots, f_ {n} ^ {\ prime} (c)\ derecha).
\ end {alineado}\]
En palabras, la derivada de\(f\) es el vector cuyas coordenadas son las derivadas de las funciones coordinadas de\(f\), reduciendo el problema de diferenciar las funciones valoradas por vector al problema de diferenciación en el cálculo de una sola variable.
Proposición\(\PageIndex{1}\)
Si\(f\) es diferenciable en\(c\) y\(f(t)=\left(f_{1}(t), f_{2}(t), \ldots, f_{n}\left(t_{0}\right)\right)\), entonces cada función de coordenadas\(f_{k}, k=1,2, \ldots, n\), es diferenciable en\(c\) y
\[ D f(c)=\left(f_{1}^{\prime}(c), f_{2}^{\prime}(c), \ldots, f_{n}^{\prime}(c)\right) .\]
Para un punto arbitrario\(t\) en el que\(f\) es diferenciable, escribiremos,
\[ D f(t)=\lim _{h \rightarrow 0} \frac{f(t+h)-f(t)}{h}=\left(f_{1}^{\prime}(t), f_{2}^{\prime}(t), \ldots, f_{n}^{\prime}(t)\right) .\]
Es decir, podemos pensar en ella misma\(Df\) como una función de valor vectorial, siendo dominio el conjunto de puntos en los que\(f\) es diferenciable.
Ahora supongamos\(f: \mathbb{R} \rightarrow \mathbb{R}^{n}\) parametriza una curva\(C\) y es diferenciable en\(c\). Si\(D f(c) \neq \mathbf{0}\), entonces la mejor aproximación afín
\[ A(t)=D f(c)(t-c)+f(c) \nonumber \]
parametriza una línea, una línea que mejor se aproxima a la curva\(C\) para los puntos cercanos\(f(c)\). Por otro lado, si\(D f(c)=\mathbf{0}\), entonces\(A\) es una función constante con rango que consiste en el punto único\(f(c)\). Estas consideraciones motivan, en parte, las siguientes definiciones.
Definición\(\PageIndex{3}\)
Supongamos que\(f: \mathbb{R} \rightarrow \mathbb{R}^{n}\) es diferenciable\((a,b)\) y\(\mathbf{x}=f(t)\) es una parametrización de una curva\(C\) para\(a<t<b\). Si\(D f(t)\) es continuo y\(D f(t) \neq \mathbf{0}\) para todos\(t\) adentro\((a,b)\), entonces llamamos\(f\) una parametrización suave de\(C\).
Definición\(\PageIndex{4}\)
Supongamos\(f: \mathbb{R} \rightarrow \mathbb{R}^{n}\) parametriza una curva\(C\) en\(\mathbb{R}^{n}\) y deja\(A\) ser la mejor aproximación afín a\(f\) at\(c\). Si\(f\) es suave en algún intervalo abierto que contiene\(c\), entonces llamamos a la línea en\(\mathbb{R}^{n}\) parametrizada por\(A\) la línea tangente a\(C\) at\(f(c)\).
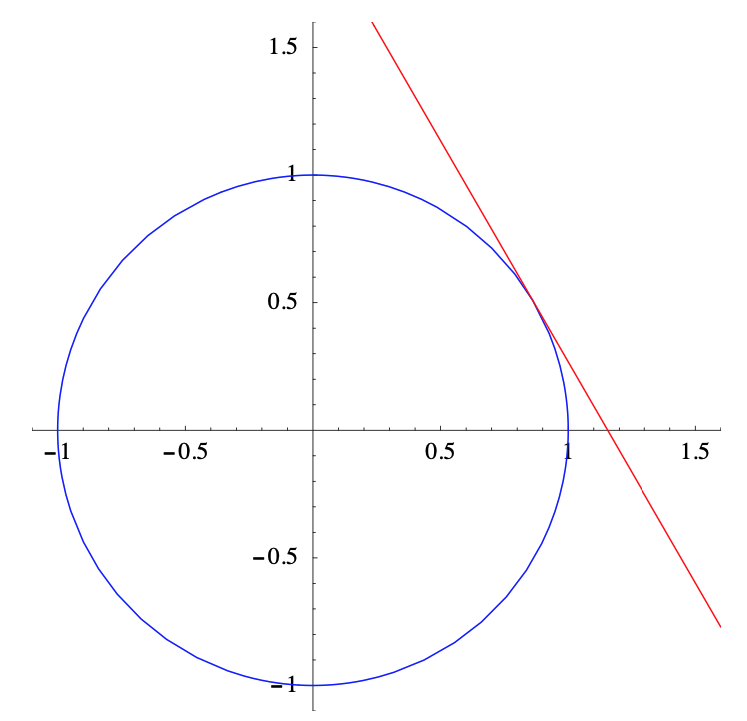
Ejemplo\(\PageIndex{1}\)
Definir\(f: \mathbb{R} \rightarrow \mathbb{R}^{n}\) por\(f(t)=(\cos (t), \sin (t))\) para\(-\infty<t<\infty\). Entonces, como vimos en la Sección 2.1,\(f\) parametriza el círculo unitario\(C\) centrado en el origen. Ahora
\[ D f(t)=(-\sin (t), \cos (t)), \nonumber \]
así\(Df(t)\) es continuo y\(\|D f(t)\|=1\) para todos\(t\). Así\(f\) es una parametrización suave de\(C\). Por ejemplo,
\[ D f\left(\frac{\pi}{6}\right)=\left(-\frac{1}{2}, \frac{\sqrt{3}}{2}\right) \nonumber \]
y
\[ f\left(\frac{\pi}{6}\right)=\left(\frac{\sqrt{3}}{2}, \frac{1}{2}\right) , \nonumber \]
así que la mejor aproximación afín a\(f\) at\(t=\frac{\pi}{6}\) es
\[ A(t)=\left(-\frac{1}{2}, \frac{\sqrt{3}}{2}\right)\left(t-\frac{\pi}{6}\right)+\left(\frac{\sqrt{3}}{2}, \frac{1}{2}\right) . \nonumber \]
La Figura 2.2.1 muestra\(C\) junto con la línea tangente\(C\) a\(t=\frac{\pi}{6}\)
Ejemplo\(\PageIndex{2}\)
Supongamos que definimos\(g: \mathbb{R} \rightarrow \mathbb{R}^{2}\) por\(g(t)=(\sin (2 \pi t), \cos (2 \pi t))\),\(-\infty<t<\infty\). Entonces, como vimos en la Sección 2.1,\(g\) parametriza el\(C\) mismo círculo que\(f\) en el ejemplo anterior. Además,
\[ D g(t)=(2 \pi \cos (2 \pi t),-2 \pi \sin (2 \pi t)) \nonumber \]
y\(\|D g(t)\|=1\) para todos\(t\), también lo\(g\) es una parametrización suave de\(C\). Sin embargo,
\[ g\left(\frac{1}{6}\right)=\left(\frac{\sqrt{3}}{2}, \frac{1}{2}\right)=f\left(\frac{\pi}{6}\right) ; \nonumber \]
es decir,\(g(t)\) es en\(\left(\frac{\sqrt{3}}{2}, \frac{1}{2}\right)\) cuando\(t=\frac{1}{6}\), mientras que\(f(t)\) es en\(\left(\frac{\sqrt{3}}{2}, \frac{1}{2}\right)\) cuando\(t=\frac{\pi}{6}\). Además,
\[ D g\left(\frac{1}{6}\right)=(\pi,-\pi \sqrt{3}), \nonumber \]
así que la mejor aproximación afín a\(g\) at\(t=\frac{1}{6}\) es
\[ B(t)=(\pi,-\pi \sqrt{3})\left(t-\frac{1}{6}\right)+\left(\frac{\sqrt{3}}{2}, \frac{1}{2}\right) . \nonumber \]
Tenga en cuenta que aunque\(A\), la mejor aproximación afín a\(f\) at\(t=\frac{1}{6}\), y\(B\), la mejor aproximación afín a\(g\) at\(t=\frac{1}{6}\), son funciones diferentes, parametrizan la misma línea ya que
\[ (\pi,-\pi \sqrt{3})=-2 \pi\left(-\frac{1}{2}, \frac{\sqrt{3}}{2}\right) .\nonumber \]
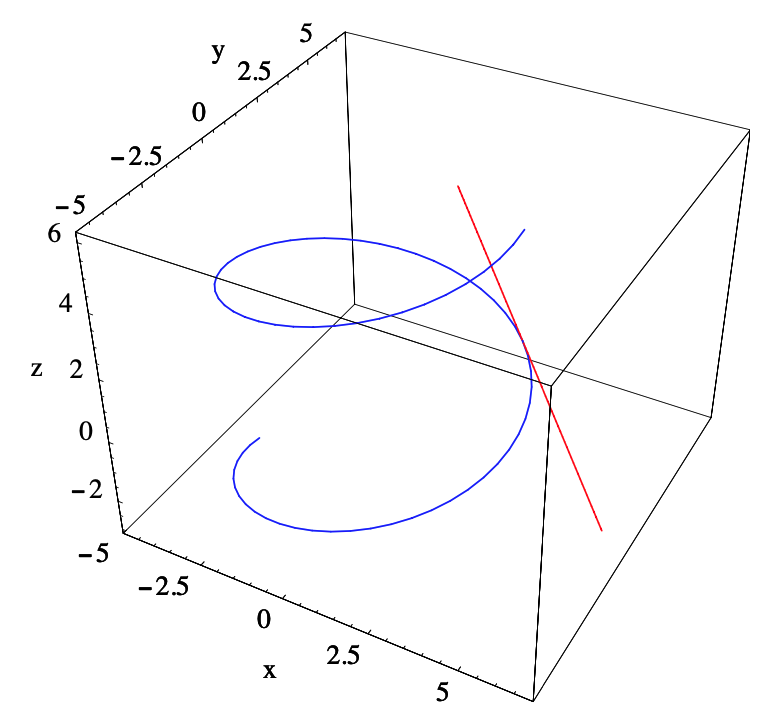
Ejemplo\(\PageIndex{3}\)
Considere la hélice\(C\) parametrizada por\(f: \mathbb{R} \rightarrow \mathbb{R}^{3}\) definida por
\[ f(t)=(4 \cos (t), 4 \sin (t), t) . \nonumber \]
Entonces
\[ D f(t)=(-4 \sin (t), 4 \cos (t), 1) .\nonumber \]
Dado que\(Df\) es continuo y
\[ \|D f(t)\|=\sqrt{16 \sin ^{2}(t)+16 \cos ^{2}(t)+1}=\sqrt{17} \nonumber \]
para todos\(t\),\(f\) es una parametrización suave de\(C\). Ahora, por ejemplo,
\[ D f\left(\frac{\pi}{4}\right)=\left(-\frac{4}{\sqrt{2}}, \frac{4}{\sqrt{2}}, 1\right)=(-2 \sqrt{2}, 2 \sqrt{2}, 1) \nonumber \]
y
\[ f\left(\frac{\pi}{4}\right)=\left(\frac{4}{\sqrt{2}}, \frac{4}{\sqrt{2}}, \frac{\pi}{4}\right)=\left(2 \sqrt{2}, 2 \sqrt{2}, \frac{\pi}{4}\right),\nonumber \]
así que la mejor aproximación afín a\(f\) at\(t=\frac{\pi}{4}\) es
\[ A(t)=(-2 \sqrt{2}, 2 \sqrt{2}, 1)\left(t-\frac{\pi}{4}\right)+\left(2 \sqrt{2}, 2 \sqrt{2}, \frac{\pi}{4}\right) .\nonumber \]
La hélice\(C\) y la línea parametrizada por\(A\), es decir, la línea tangente a\(C\) at\(t=\frac{\pi}{4}\), se muestran en la Figura 2.2.2.
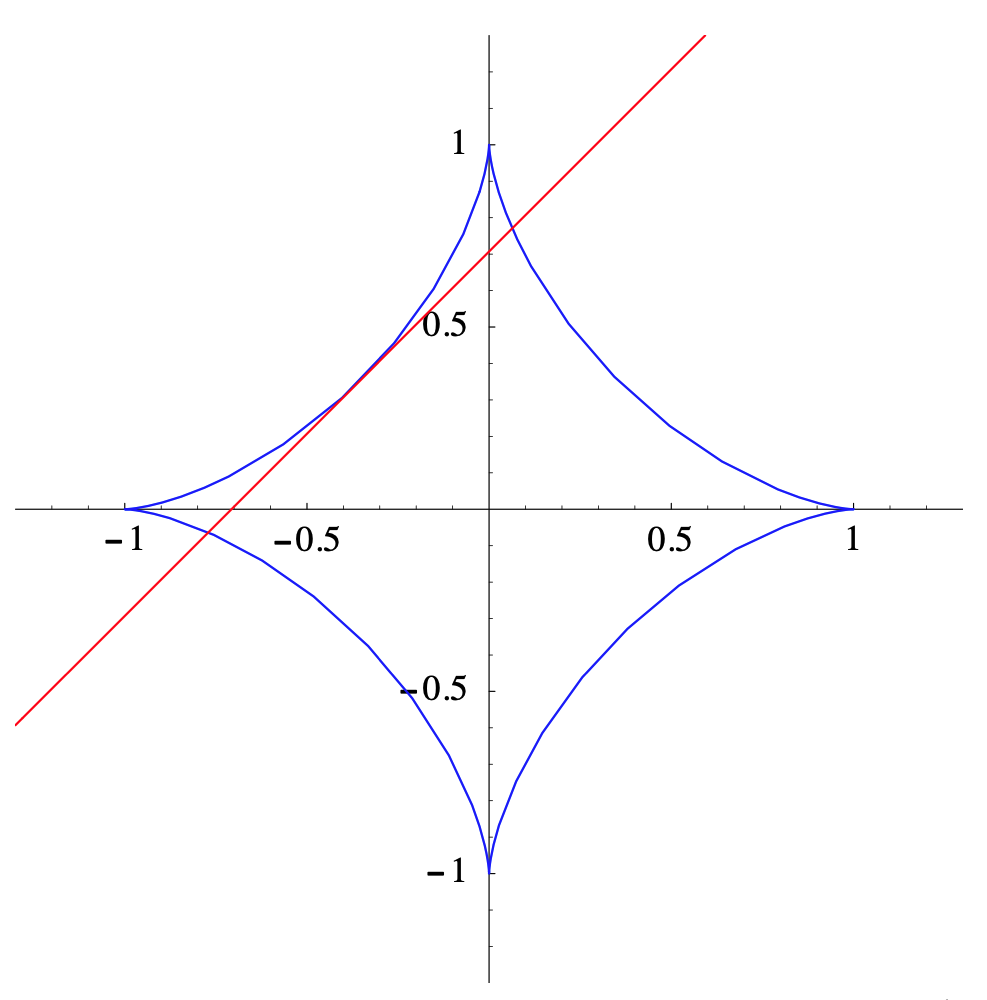
Ejemplo\(\PageIndex{4}\)
Dejar\(C\) ser la curva en\(\mathbb{R}^2\) parametrizada por
\[ h(t)=\left(\cos ^{3}(t), \sin ^{3}(t)\right) . \nonumber \]
Entonces
\[ D h(t)=\left(-3 \cos ^{2}(t) \sin (t), 3 \sin ^{2}(t) \cos (t)\right) . \nonumber \]
De ahí\(Dh\) que sea continuo para todos\(t\), pero no\(h\) es una parametrización suave de\(C\) ya que\(D h(t)=\mathbf{0}\) siempre\(t\) es un múltiplo entero de\(\frac{pi}{2}\). Estos puntos corresponden a las esquinas agudas de\(C\) at (1, 0), (0, 1), (−1, 0 y (0, −1), como se muestra en la Figura 2.2.3. Sin embargo,\(h\) es una parametrización suave de los cuatro arcos de los\(C\) cuales se parametrizan restringiendo\(h\) a los intervalos abiertos\(\left(0, \frac{\pi}{2}\right),\left(\frac{\pi}{2}, \pi\right),\left(\pi, \frac{3 \pi}{2}\right)\), y\(\left(\frac{3 \pi}{2}, 2 \pi\right)\). De ahí, por ejemplo, señalar que
\[ D h\left(\frac{3 \pi}{4}\right)=\left(-\frac{3}{2 \sqrt{2}},-\frac{3}{2 \sqrt{2}}\right) \nonumber \]
y
\[ h\left(\frac{3 \pi}{4}\right)=\left(-\frac{1}{2 \sqrt{2}}, \frac{1}{2 \sqrt{2}}\right) ,\nonumber \]
encontramos que la mejor aproximación afín a\(h\) at\(t=\frac{3 \pi}{4}\) es
\[ A(t)=\left(-\frac{3}{2 \sqrt{2}},-\frac{3}{2 \sqrt{2}}\right)\left(t-\frac{3 \pi}{4}\right)+\left(-\frac{1}{2 \sqrt{2}}, \frac{1}{2 \sqrt{2}}\right) .\nonumber \]
La línea tangente parametrizada por\(A\) se muestra en la Figura 2.2.3.
Proposición\(\PageIndex{2}\)
Supongamos\(f: \mathbb{R} \rightarrow \mathbb{R}^{n}\)\(g: \mathbb{R} \rightarrow \mathbb{R}^{n}\),, y\(\varphi: \mathbb{R} \rightarrow \mathbb{R}\) son todos diferenciables. Entonces
\ [\ begin {align}
D (f (t) +g (t)) =D f (t) +D g (t),\ label {2.2.19}\\
D (f (t) -g (t)) =D f (t) -D g (t),\ etiqueta {2.2.20}\\
D (\ varphi (t) f (t)) =\ varphi (t)) =\ varphi (t)) D f (t) +\ varphi^ {\ prime} (t) f (t),\ label {2.2.21}
\\\ frac {d} {d t} (f (t)\ cdot g (t)) =f (t)\ cdot D g (t) +D f (t)\ cdot g ( t),\ label {2.2.22}
\ end {align}\]
y
\[ D\left(f(\varphi(t))=D f(\varphi(t)) \varphi^{\prime}(t)\right) . \label{2.2.23}\]
Tenga en cuenta que todas las declaraciones en esta proposición se reducen a los resultados familiares del cálculo de una variable cuando\(n=1\). Para verificar estos resultados, vamos
\[ f(t)=\left(f_{1}(t), f_{2}(t), \ldots, f_{n}(t)\right) \nonumber \]
y
\[ g(t)=\left(g_{1}(t), g_{2}(t), \ldots, g_{n}(t)\right) .\nonumber \]
Entonces
\ [\ begin {align}
D (f (t) +g (t)) &=D\ izquierda (f_ {1} (t) +g_ {1} (t), f_ {2} (t) +g_ {2} (t),\ ldots, f_ {n} (t) +g_ {n} (t)\ derecha)\ nonumber\\
&= izquierda (f_ {1} ^ {\ prime} (t) +g_ {1} ^ {\ prime} (t), f_ {2} ^ {\ prime} (t) +g_ {2} ^ {\ prime} (t),\ ldots, f_ {n} ^ {\ prime} (t) +g_ {n} ^ {\ prime} (t)\ derecha)\ etiqueta {}\\
&=\ left (f_ {1} ^ {\ prime} (t), f_ {2} ^ {\ prime} (t),\ ldots, f_ {n} ^ {\ prime} (t)\ right) +\ left (g_ {1} ^ {\ prime} (t), g_ {2} ^ {\ prime} (t),\ ldots, g_ {n} ^ {\ prime} (t)\ derecha)\ nonumber\\
&=D f (t) +D g (t),\ nonumber
\ end {align}\]
verificar (\(\ref{2.2.19}\)). La verificación de (2.1.20) es similar. Las demostraciones de (\(\ref{2.2.21}\)) y (2.1.22), ambas generalizaciones de la regla del producto a partir del cálculo de una variable, siguen fácilmente a partir de ese resultado; verificaremos (2.1.22) aquí y dejaremos (\(\ref{2.2.21}\)) para el Ejercicio 13. Usando la regla del producto, tenemos
\ [\ begin {align}
\ frac {d} {d} {d t} (f (t)\ cdot g (t)) =&\ frac {d} {d} {d t}\ izquierda (f_ {1} (t) g_ {1} (t) +f_ {2} (t) g_ {2} (t) +\ cdots+f_ {n} (t) g_ {n} (t)\ derecha)\ nonumber\\
=& f_ {1} (t) g_ {1} ^ {\ prime} (t) +f_ {1} ^ {\ prime} (t) g_ {1} (t) +f_ {2} (t) g_ {2} ^ {\ prime} (t) +f_ {2} ^ {prime\} (t) g_ {2} (t) +\ cdots\ etiqueta {} \\
&\ cuádruple f_ {n} (t) g_ {n} ^ {\ prime} (t) +f_ {n} ^ {\ prime} (t) g_ {n} (t)\ nonumber\\
=& f (t)\ cdot D g (t) +D f (t)\ cdot g (t). \ nonumber
\ end {align}\]
Finalmente, (\(\ref{2.2.23}\)), una generalización de la regla de cadena a partir del cálculo de una variable, sigue directamente de ese resultado:
\ [\ begin {align}
D (f (\ varphi (t))) &=D\ izquierda (f_ {1} (\ varphi (t)), f_ {2} (\ varphi (t)),\ ldots, f_ {n} (\ varphi (t))\ derecha)\ nonumber\\
&=\ izquierda (f_ {1} ^ {prime\} (\ varphi (t))\ varphi^ {\ prime} (t), f_ {2} ^ {\ prime} (\ varphi (t))\ varphi^ {\ prime} (t),\ ldots, f_ {n} ^ {\ prime} (\ varphi (t))\ varphi (t))\ varphi^ {\ prime} (t)\ derecha)\ label {}\\
&=D f (\ varphi (t))\ varphi^ {\ prime} (t). \ nonumber
\ end {align}\]
Reparametrizaciones
Hemos visto arriba que la parametrización de una curva\(C\) en no\(\mathbb{R}^n\) es única. Por ejemplo, vimos que ambos\(f(t)=(\cos (t), \sin (t))\) y\(g(t)=(\sin (2 \pi t), \cos (2 \pi t))\) parametrizar el círculo unitario centrado en el origen. Sin embargo, también notamos que las mejores aproximaciones afinas para las dos parametrizaciones, aunque funciones distintas, sin embargo parametrizan la misma línea en\(\left(\frac{\sqrt{3}}{2}, \frac{1}{2}\right)\), la línea que hemos venido llamando la línea tangente. Debemos sospechar que este será el caso en general, es decir, la línea tangente a una curva\(C\) en un punto determinado no debe depender de la parametrización particular de\(C\) utilizada en el cálculo. Al tiempo que evitamos algunos tecnicismos, proporcionaremos alguna justificación para estas ideas.
Definición\(\PageIndex{5}\)
Supongamos\(\mathbf{x}=f(t), a<t<b\), es una parametrización suave de una curva\(C\) en\(\mathbb{R}^n\). Supongamos que\(\varphi: \mathbb{R} \rightarrow \mathbb{R}\) tiene dominio\((c,d)\)\((a,b)\), rango, y\(\varphi^{\prime}\) existe y es continuo en\((c,d)\). Si\(\varphi^{\prime}(t) \neq 0\) para todos\(t\) en\((c,d)\), entonces llamamos\(g(t)=f(\varphi(t))\) una reparametrización de\(f\).
Ejemplo\(\PageIndex{5}\)
Dejar\(f(t)=(\cos (t), \sin (t))\) y\(g(t)=(\sin (2 \pi t), \cos (2 \pi t))\). Desde
\[ \sin (t)=\cos \left(\frac{\pi}{2}-t\right) \nonumber \]
y
\[\cos (t)=\sin \left(\frac{\pi}{2}-t\right), \nonumber \]
se deduce que
\[ g(t)=f\left(\frac{\pi}{2}-2 \pi t\right)=f(\varphi(t)), \nonumber \]
donde
\[ \varphi(t)=\frac{\pi}{2}-2 \pi t . \nonumber \]
Es decir,\(g\) es una reparametrización de\(f\).
Ahora bien\(\mathbf{x}=f(t), a<t<b\), si, es una parametrización suave de una curva\(C\) en\(\mathbb{R}^n\) y\(g(t)=f(\varphi(t)), c<t<d\), es una reparametrización de\(f\), entonces para cualquiera\(\alpha\) en\((c,d)\),
\[ D g(\alpha)=D\left(f(\varphi(\alpha))=D f(\varphi(\alpha)) \varphi^{\prime}(\alpha)\right. . \]
De ahí\(Dg(\alpha)\) y\(D f(\varphi(\alpha))\) son paralelos, siendo los primeros los segundos multiplicados por el escalar\(\varphi^{\prime}(\alpha)\). En otras palabras, las líneas parametrizadas por la mejor aproximación afín a\(g\) at\(t=\alpha\) y la mejor aproximación afín a\(f\) at\(t=\varphi(\alpha)\) son las mismas.
Ejemplo\(\PageIndex{6}\)
En nuestro ejemplo anterior, tenemos
\[ \varphi^{\prime}(t)=-2 \pi , \nonumber \]
así que, para cualquiera\(\alpha\), deberíamos tener
\[ D g(\alpha)=-2 \pi D f(\varphi(\alpha)). \nonumber \]
Esto concuerda con nuestro cálculo anterior utilizando\(\alpha=\frac{1}{6}\).
Vectores tangentes y normales
Si\(f: \mathbb{R} \rightarrow \mathbb{R}^{n}\) es una parametrización suave de una curva\(C\), entonces, para cualquiera\(t\),\(Df(t)\) es la dirección de la línea tangente a\(C\) at\(f(t)\). Además, de nuestra discusión anterior, si\(g\) es una reparametrización de\(f\), digamos\(g(t)=f(\varphi(t))\),, entonces\(Dg(t)\) y\(D f(\varphi(t))\) tendrá la misma dirección u opuesta. En otras palabras, la dirección de la línea tangente o bien permanece igual o se invierte bajo reparametrización. Por otra parte,
\[ \|D g(t)\|=\|D f(\varphi(t))\|\left|\varphi^{\prime}(t)\right| .\]
Como debemos esperar, aunque ambos\(Dg(t)\) y\(D f(\varphi(T))\) son tangentes a la curva en\(g(t)\), sus longitudes no tienen que ser las mismas. En la Sección 2.3 discutiremos cómo podemos pensar de esto en términos de la velocidad de una partícula que se mueve a lo largo de la curva\(C\), con su posición encendida\(C\) en el tiempo t dada por cualquiera\(g(t)\) o\(f(t)\).
Para estas y otras consideraciones, es útil definir un vector tangente estándar, único hasta un cambio en el signo.
Definición\(\PageIndex{6}\)
Si\(f: \mathbb{R} \rightarrow \mathbb{R}^{n}\) es una parametrización suave de una curva\(C\), entonces llamamos
\[ T(t)=\frac{D f(t)}{\|D f(t)\|} \]
el vector tangente unitario a\(C\) at\(f(t)\).
De lo anterior, debemos tener en cuenta que el vector tangente unitario siempre\(T(t)\) está en referencia a alguna parametrización\(f\) de la curva\(C\). Esencialmente, se trata de una elección de una orientación para la curva, es decir, la dirección del movimiento de una partícula cuya posición en el momento\(t\) viene dada por\(f(t)\).
Si\(\mathbf{x}=f(t), a<t<b\), es una parametrización suave de una curva\(C\) en\(\mathbb{R}^n\), entonces, por definición,\(\|T(t)\|=1\) para all\(t\) in\((a,b)\). De ahí
\[ T(t) \cdot T(t)=1 \label{2.2.30} \]
para todos\(t\) en\((a,b)\). Diferenciando (\(\ref{2.2.30}\)), tenemos
\[ \frac{d}{d t}(T(t) \cdot T(t))=\frac{d}{d t} 1=0 ,\]
y así, usando (\(\ref{2.2.22}\)), tenemos
\[ 0=\frac{d}{d t}(T(t) \cdot T(t))=T(t) \cdot D T(t)+D T(t) \cdot T(t)=2 D T(t) \cdot T(t) \]
para todos\(t\) en\((a,b)\). Así\(T(t) \cdot D T(t)=0\) para\(a<t<b\). En otras palabras,\(DT(t)\) es ortogonal a\(T(t)\) para todos\(t\) en\((a,b)\).
Definición\(\PageIndex{7}\)
Si\(f: \mathbb{R} \rightarrow \mathbb{R}^{n}\) es una parametrización suave de una curva\(C\),\(T(t)\) es la unidad tangente vector a\(C\) at\(f(t)\), y\(D T(t) \neq \mathbf{0}\), entonces llamamos
\[ N(t)=\frac{D T(t)}{\|D T(t)\|} \]
la unidad principal vector normal a\(C\) at\(f(t)\).
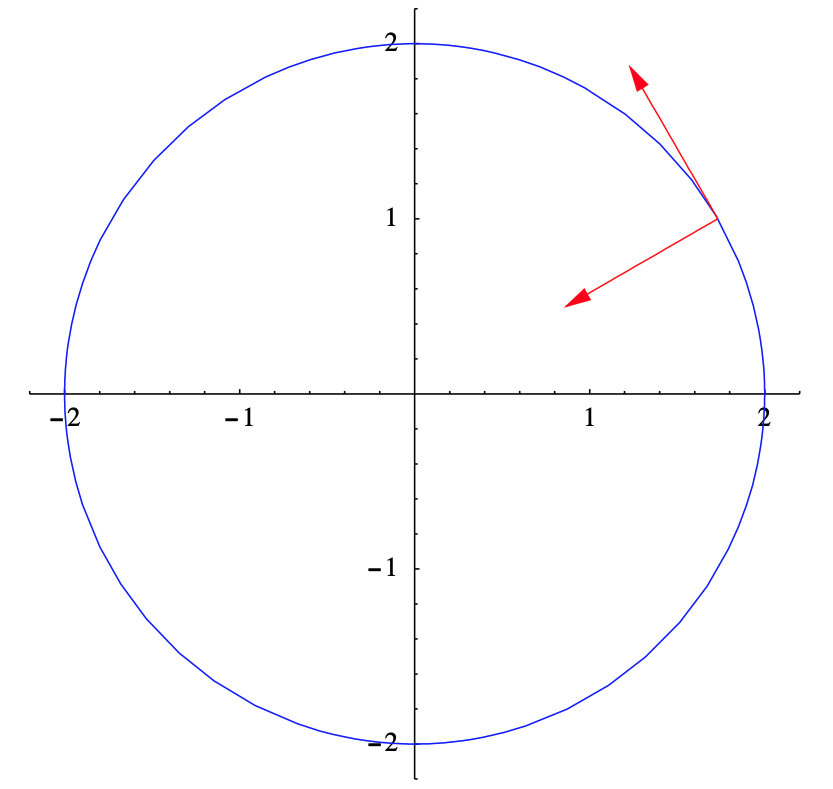
Ejemplo\(\PageIndex{7}\)
Considere la parametrización del círculo\(\mathbb{R}^2\) con radio 2 y centro en el origen dado por
\[ f(t)=(2 \cos (4 t), 2 \sin (4 t)) . \nonumber \]
Entonces
\[ D f(t)=(-8 \sin (4 t), 8 \cos (4 t)) \nonumber \]
y
\[ \|D f(t)\|=\sqrt{64 \sin ^{2}(4 t)+64 \cos ^{2}(4 t)}=8 . \nonumber \]
Así, el vector tangente unitario es
\[ T(t)=\frac{D f(t)}{\|D f(t)\|}=(-\sin (4 t), \cos (4 t)) . \nonumber \]
Además,
\[ D T(t)=(-4 \cos (t),-4 \sin (4 t)) , \nonumber \]
entonces
\[ \|D T(t)\|=\sqrt{16 \cos ^{2}(4 t)+16 \sin ^{2}(4)}=4 , \nonumber \]
y el vector normal de la unidad principal es
\[ N(t)=\frac{D T(t)}{\|D T(t)\|}=(-\cos (4 t),-\sin (4 t)) . \nonumber \]
Por ejemplo, cuando\(t=\frac{\pi}{24}\) tenemos
\ [\ begin {reunió}
f\ izquierda (\ frac {\ pi} {24}\ derecha) =(\ sqrt {3}, 1),\\
T\ izquierda (\ frac {\ pi} {24}\ derecha) =\ izquierda (-\ frac {1} {2},\ frac {\ sqrt {3}} {2}\ derecha),
\ final reunido}\]
y
\[ N\left(\frac{\pi}{24}\right)=\left(-\frac{\sqrt{3}}{2},-\frac{1}{2}\right) .\nonumber \]
Tenga en cuenta que, para cualquier valor de\(t\),\(f(t) \perp T(t), T(t) \perp N(t)\) (como siempre es el caso), y\(N(t)=-\frac{1}{2} f(t)\)). Ver Figura 2.2.4.
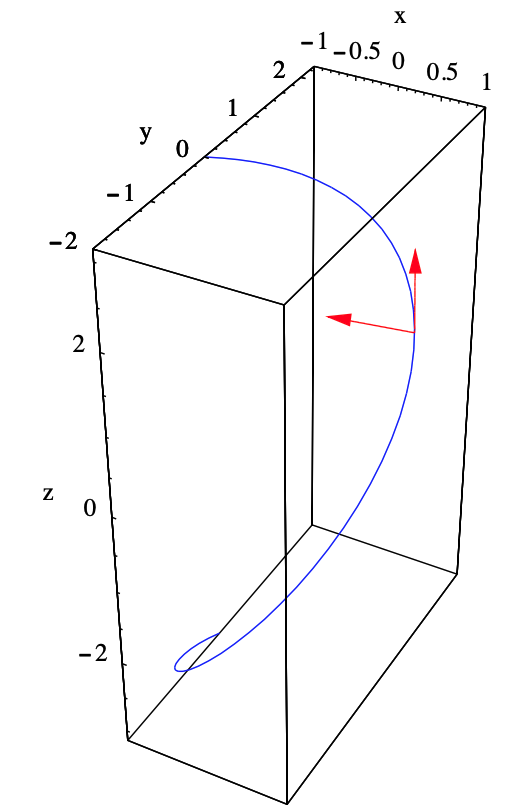
Ejemplo\(\PageIndex{8}\)
Considere la hélice elíptica\(H\) parametrizada por
\[ g(t)=(\cos (t), 2 \sin (t), t) . \nonumber \]
Entonces
\[ D g(t)=(-\sin (t), 2 \cos (t), 1), \nonumber \]
entonces
\ [\ begin {alineado}
\ |D g (t)\ | &=\ sqrt {\ sin ^ {2} (t) +4\ cos ^ {2} (t) +1}\\
&=\ sqrt {\ sin ^ {2} (t) +\ cos ^ {2} (t) +3\ cos ^ {2} (t) +1}\\
&=\ sqrt {2+3\ cos ^ {2} (t)}\\
&=\ sqrt {2+\ frac {3} {2} (1+\ cos (2 t))}\\
&=\ sqrt {\ frac {7+3\ cos (2 t)} {2}}.
\ end {alineado}\]
Por lo tanto, el vector tangente unitario es
\[ T(t)=\sqrt{\frac{2}{7+3 \cos (2 t)}}(-\sin (t), 2 \cos (t), 1) . \nonumber \]
Diferenciando usando (\(\ref{2.2.21}\)), tenemos
\ [\ begin {alineado}
D T (t) =&\ sqrt {\ frac {2} {7+3\ cos (2 t)}} (-\ cos (t), -2\ sin (t), 0)\\
&+\ frac {1} {2}\ izquierda (\ frac {2} {7+3\ cos (2 t)}\ derecha) ^ {-\ frac {1} {2}}\ izquierda (\ frac {12\ sin (2 t)} {(7+3\ cos (2 t)) ^ {2}}\ derecha) (-\ sin (t), 2\ cos (t), 1)\\
=&\ sqrt {\ frac {2} { 7+3\ cos (2 t)}} (-\ cos (t), -2\ sin (t), 0) +\ frac {3\ sqrt {2}\ sin (2 t)} {(7+3\ cos (2 t)) ^ {\ frac {3} {2}}} (-\ sin (t), 2\ cos (t), 1).
\ end {alineado}\]
Por ejemplo, en\(t=\frac{\pi}{4}\) tenemos
\ [\ begin {alineado}
g\ izquierda (\ frac {\ pi} {4}\ derecha) &=\ izquierda (\ frac {1} {\ sqrt {2}},\ sqrt {2},\ frac {\ pi} {4}\ derecha),\\
T\ izquierda (\ frac {\ pi} {4}\ derecha) &=\ frac {1} {sqrt {7}} (-1,2,\ sqrt {2}),
\ end {alineado}\]
y
\[ D T\left(\frac{\pi}{4}\right)=\frac{1}{\sqrt{7}}(-1,-2,0)+\frac{3}{7^{\frac{3}{2}}}(-1,2, \sqrt{2})=\frac{1}{7 \sqrt{7}}(-10,-8,3 \sqrt{2}) . \nonumber \]
Así
\[ \left\|D T\left(\frac{\pi}{4}\right)\right\|=\frac{1}{7 \sqrt{7}} \sqrt{100+64+18}=\frac{\sqrt{26}}{7} , \nonumber \]
por lo que el vector normal de la unidad principal\(t=\frac{\pi}{4}\) es
\[ N\left(\frac{\pi}{4}\right)=\frac{D T\left(\frac{\pi}{4}\right)}{\left\|D T\left(\frac{\pi}{4}\right)\right\|}=\frac{1}{\sqrt{182}}(-10,-8,3 \sqrt{2}) . \nonumber \]
Ver Figura 2.2.5
Como muestra el último ejemplo, pueden involucrarse los cálculos involucrados en la búsqueda del vector tangente unitario y el vector normal de la unidad principal. De hecho, es por eso que calculamos el vector normal de la unidad principal solo en el caso particular\(t=\frac{\pi}{4}\) en lugar de escribir la fórmula general para\(N(t)\). En general estos cálculos pueden involucrarse lo suficiente como para que a menudo sea prudente hacer uso de un sistema de álgebra computacional.


