3.1: Geometría, límites y continuidad

En este capítulo estudiaremos funciones\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\), funciones que toman vectores para entradas y dan escalares para salidas. Por ejemplo, la función que toma un punto en el espacio para entrada y devuelve la temperatura en ese punto es tal función; la función que reporta el producto nacional bruto de un país es otra de esas funciones. Obsérvese que el espacio de dominio del primer ejemplo es tridimensional, mientras que el dominio de este último tiene, para la mayoría de los países, miles de dimensiones. Como es habitual, siempre que sea posible expondremos nuestros resultados para un espacio arbitrario\(n\) -dimensional, aunque la mayoría de nuestros ejemplos tratarán solo de dos o tres dimensiones.

Conjuntos de niveles y gráficos

Comenzamos considerando algunos métodos geométricos para la representación de funciones de la forma\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\).

Definición\(\PageIndex{1}\)

Dada una función\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\) y un número real\(c\), llamamos al conjunto

\[ L=\left\{\left(x_{1}, x_{2}, \ldots, x_{n}\right): f\left(x_{1}, x_{2}, \ldots, x_{n}\right)=c\right\} \]

un conjunto de niveles de\(f\) a nivel\(c\). También llamamos\(L\) un contorno de\(f\). Cuando\(n=2\), llamamos\(L\) una curva de nivel de\(f\) y cuando\(n=3\) llamamos\(L\) una superficie nivelada de\(f\). Una gráfica que muestra conjuntos de niveles para varios niveles diferentes se denomina gráfica de contorno.

Ejemplo\(\PageIndex{1}\)

Supongamos que\(f: \mathbb{R}^{2} \rightarrow \mathbb{R}\) está definido por

\[ f(x, y)=2 x^{2}+y^{2} . \nonumber \]

Dado un número real\(c\), el conjunto de todos los puntos satisfactorios

\[ 2 x^{2}+y^{2}=c \nonumber \]

es un conjunto de niveles de\(f\). For\(c<0\), este conjunto está vacío; for\(c=0\), consiste únicamente en el punto (0, 0); para cualquiera\(c>0\), el conjunto de niveles es una elipse con centro en (0, 0). De ahí que una gráfica de contorno de\(f\), como se muestra en la Figura 3.1.1, consiste en elipses concéntricas.

Figura\(\PageIndex{1}\): Curvas de nivel\(2 x^{2}+y^{2}=c\)

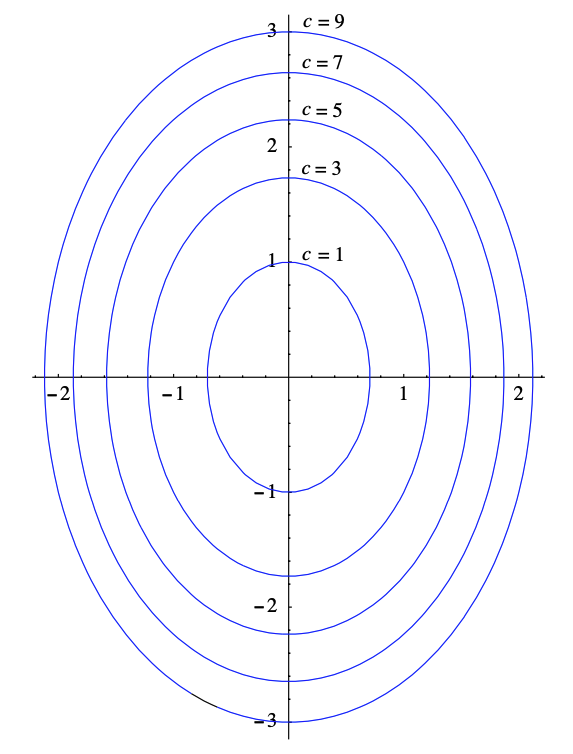
Ejemplo\(\PageIndex{2}\)

Supongamos que\(f: \mathbb{R}^{2} \rightarrow \mathbb{R}\) está definido por

\[ f(x, y)=\frac{\sin \left(\sqrt{x^{2}+y^{2}}\right)}{\sqrt{x^{2}+y^{2}}} . \nonumber \]

Para cualquier punto\((x,y)\) del círculo de radio\(r>0\) centrado en el origen,\(f(x,y)\) tiene el valor constante

\[ \frac{\sin (r)}{r} . \nonumber \]

De ahí que una gráfica de contorno de\(f\), como la que se muestra en la Figura 3.1.2, consiste en círculos concéntricos centrados en el origen.

Figura\(\PageIndex{2}\): Curvas de nivel\(\frac{\sin \left(\sqrt{x^{2}+y^{2}}\right)}{\sqrt{x^{2}+y^{2}}}=c\)

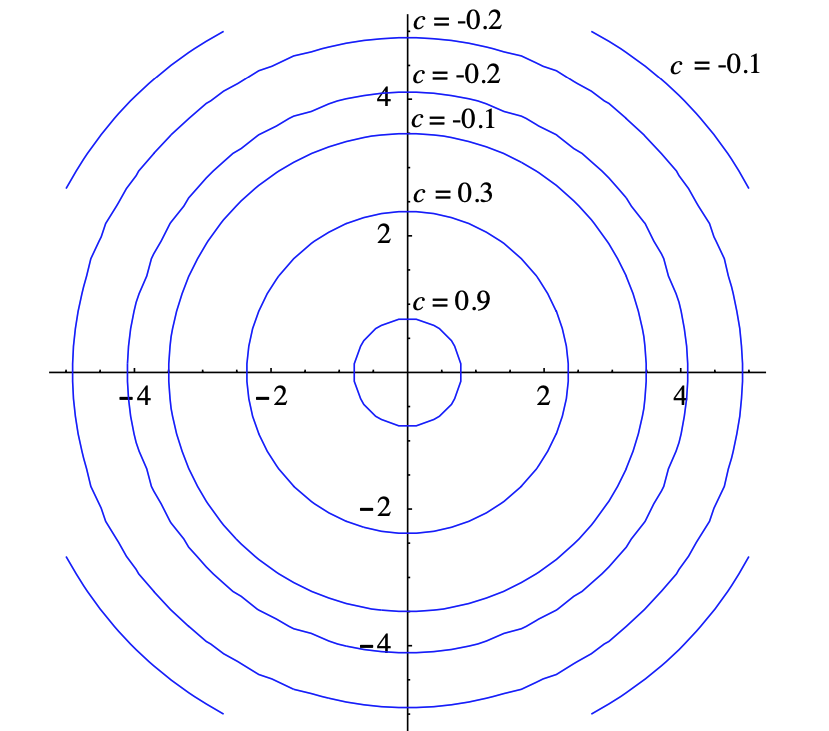
Ejemplo\(\PageIndex{3}\)

Supongamos que\(f: \mathbb{R}^{3} \rightarrow \mathbb{R}\) está definido por

\[ f(x, y, z)=x^{2}+2 y^{2}+3 z^{2} . \nonumber \]

La superficie nivelada de\(f\) con ecuación

\[ x^{2}+2 y^{2}+3 z^{2}=1 \nonumber \]

se muestra en la Figura 3.1.3. Tenga en cuenta que, por ejemplo, fijar un valor\(z_0\) de\(z\) rinde la ecuación

\[ x^{2}+y^{2}=1-3 z_{0}^{2}, \nonumber \]

la ecuación de una elipse. Esto explica por qué una porción de la superficie nivelada mostrada en la Figura 3.1.3 paralela al\(xy\) plano es una elipse. De igual manera, los cortes paralelos al\(xz\) plano -plano y al\(yz\) plano -son elipses, razón por la cual esta superficie es un ejemplo de elipsoide.

Figura\(\PageIndex{3}\): La superficie nivelada \(x^{2}+2 y^{2}+3 z^{2}=1\)

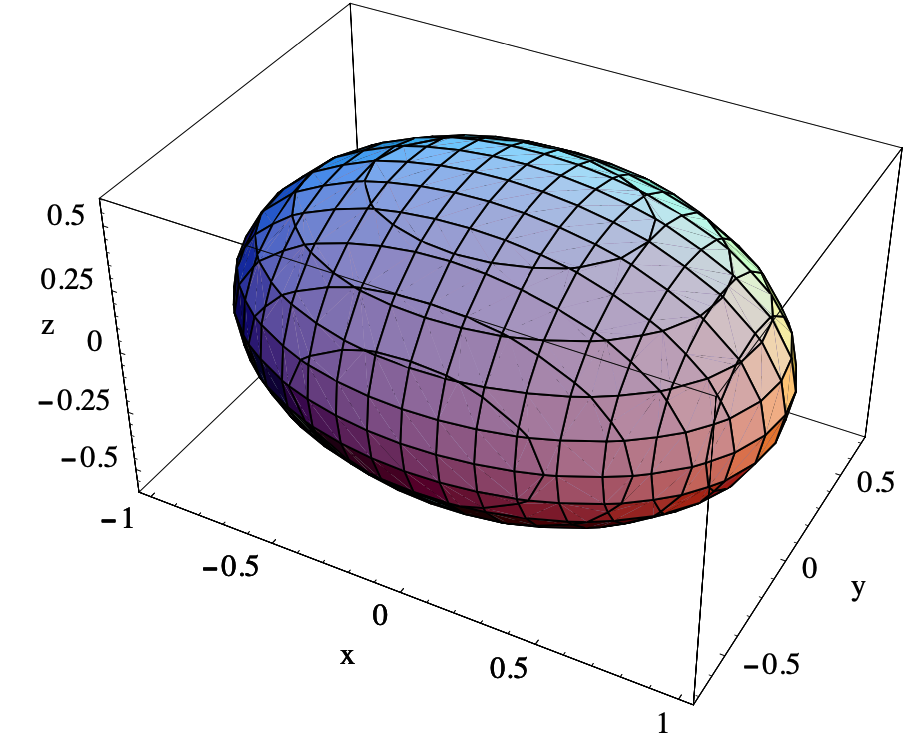
Definición\(\PageIndex{2}\)

Dada una función\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\), llamamos al conjunto

\[ G=\left\{\left(x_{1}, x_{2}, \ldots, x_{n}, x_{n+1}\right): x_{n+1}=f\left(x_{1}, x_{2}, \ldots, x_{n}\right)\right\} \]

la gráfica de\(f\).

Tenga en cuenta que la gráfica\(G\) de una función\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\) está en\(R^{n+1}\). Como consecuencia, podemos imaginarnos\(G\) sólo si\(n=1\), en cuyo caso\(G\) es una curva como se estudia en el cálculo de una sola variable, o\(n=2\), en cuyo caso\(G\) es una superficie en\(\mathbb{R}^{3}\).

Ejemplo\(\PageIndex{4}\)

Considere la función\(f: \mathbb{R}^{2} \rightarrow \mathbb{R}\) definida por

\[ f(x, y)=2 x^{2}+y^{2} . \nonumber \]

La gráfica de\(f\) es entonces el conjunto de todos los puntos\((x,y,z)\) en los\(\mathbb{R}^{3}\) que satisfacen la ecuación\(z=2 x^{2}+y^{2}\). Una forma de imaginar la gráfica de\(f\) es imaginar elevar las curvas de nivel en la Figura 3.1.1 a sus respectivas alturas por encima del\(xy\) plano, creando la superficie que\(\mathbb{R}^{3}\) se muestra en la Figura 3.1.4. Otra forma de imaginar la gráfica es considerar cortes de la gráfica que se encuentran por encima de una cuadrícula de líneas paralelas a los ejes en el\(xy\) plano. Por ejemplo, para un valor fijo de\(x\), digamos\(x_0\), el conjunto de puntos que satisfacen la ecuación\(z=2 x_{0}^{2}+y^{2}\) es una parábola que se encuentra por encima de la línea\(x=x_0\). De igual manera, fijar un valor\(y_0\) de\(y\) arroja la parábola que se\(z=2 x^{2}+y_{0}\) encuentra por encima de la línea\(y=y_0\). Si dibujamos estas parábolas para numerosas líneas de la forma\(x=x_0\) y\(y=y_0\), obtenemos un alambre-marco de la gráfica. La gráfica mostrada en la Figura 3.1.4 se obtuvo rellenando los parches superficiales de una malla de alambre-marco, cuyo contorno es visible en la superficie. Esta superficie es un ejemplo de un paraboloide.

Figura\(\PageIndex{4}\): El paraboloide\(z=2 x^{2}+y^{2}\)

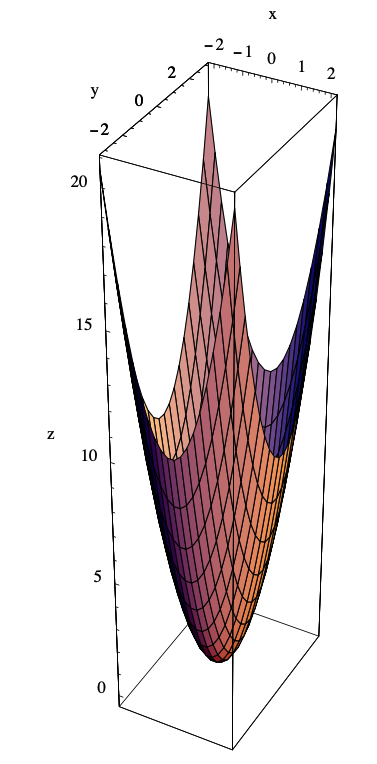
Ejemplo\(\PageIndex{5}\)

Si bien las gráficas de muchas funciones pueden ser esbozadas razonablemente bien a mano utilizando las ideas del ejemplo anterior, para la mayoría de las funciones una buena imagen de su gráfica requiere ya sea gráficos por computadora o considerable habilidad artística. Por ejemplo, considere la gráfica de

\[ f(x, y)=\frac{\sin \left(\sqrt{x^{2}+y^{2}}\right)}{\sqrt{x^{2}+y^{2}}} . \nonumber \]

Usando la gráfica de contorno, podemos imaginar cómo la gráfica de\(f\) oscila a medida que nos alejamos del origen, los círculos de nivel de la gráfica de contorno suben y bajan con las oscilaciones de

\[ \frac{\sin (r)}{r} , \nonumber \]

donde\(r=\sqrt{x^{2}+y^{2}}\). Equivalentemente, la porción de la gráfica por encima de cualquier línea a través del origen será la gráfica de

\[ z=\frac{\sin (r)}{r} . \nonumber \]

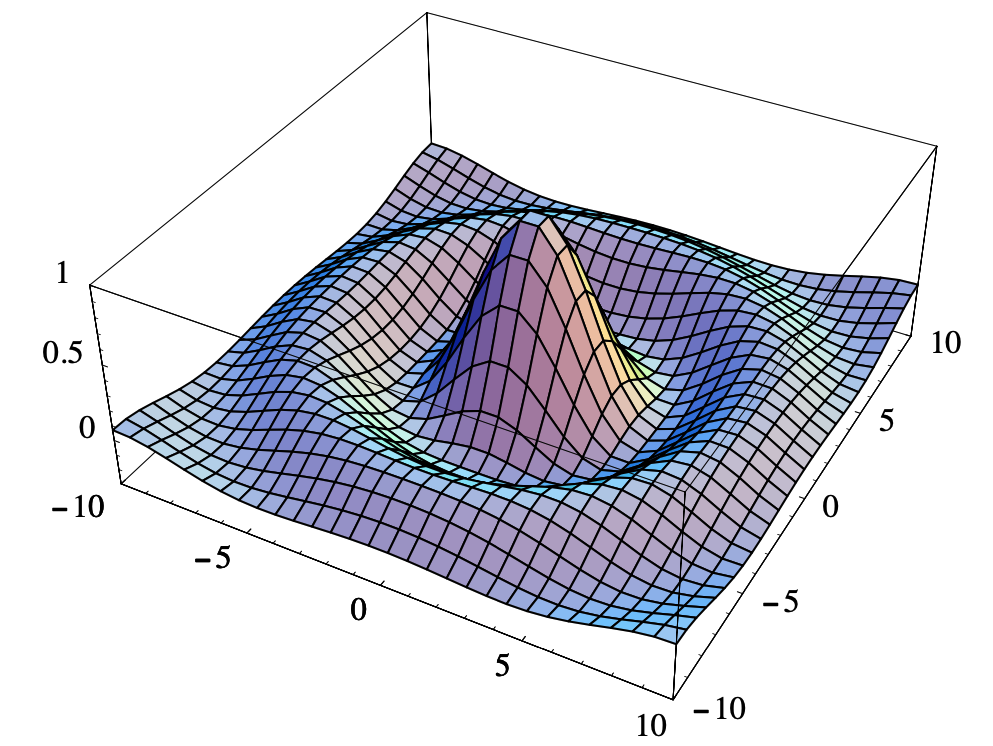
Esto debería darte una buena idea de cómo es la gráfica de\(f\), pero, sin embargo, la mayoría de nosotros no podríamos producir la imagen de la Figura 3.1.5 sin la ayuda de una computadora. Observe que aunque no\(f\) se define en (0, 0), parece que se\(f(x,y)\) acerca a 1 como se\((x,y)\) acerca a 0. Esto es de hecho cierto, consecuencia del hecho de que

\[ \lim _{r \rightarrow 0} \frac{\sin (r)}{r}=1 . \nonumber \]

Volveremos a este ejemplo después de haber introducido límites y continuidad.

Figura\(\PageIndex{5}\): Gráfica de\(f(x, y)=\frac{\sin \left(\sqrt{x^{2}+y^{2}}\right)}{\sqrt{x^{2}+y^{2}}}\)

Límites y continuidad

A estas alturas las dos definiciones siguientes deberían resultar familiares.

Definición\(\PageIndex{3}\)

Dejar\(\mathbf{a}\) ser un punto de entrada\(\mathbb{R}^{n}\) y dejar\(O\) ser el conjunto de todos los puntos en la bola abierta de radio\(r>0\) centrada en\(\mathbf{c}\) excepto en\(\mathbf{c}\) sí mismo. Es decir,

\[ O=\left\{\mathbf{x}: \mathbf{x} \text { is in } B^{n}(\mathbf{c}, r), \mathbf{x} \neq \mathbf{c}\right\} . \]

Supongamos que\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\) se define para todos\(\mathbf{x}\) en\(O\). Decimos que el límite de\(f(\mathbf{x})\) como\(x\) enfoques\(\mathbf{c}\) es\(L\), escrito\(\lim _{\mathbf{x} \rightarrow \mathbf{c}} f(\mathbf{x})=L\), si por cada secuencia de puntos\(\left\{\mathbf{x}_{m}\right\}\) en\(O\),

\[ \lim _{m \rightarrow \infty} f\left(\mathbf{x}_{m}\right)=L \]

cuando sea\(\lim _{m \rightarrow \infty} \mathbf{x}_{m}=\mathbf{c}\).

Definición\(\PageIndex{4}\)

Supongamos que\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\) se define para todos\(\mathbf{x}\) en alguna bola abierta\(B^{n}(\mathbf{c}, r), r>0\). Decimos que\(f\) es continuo en\(\mathbf{c}\) si

\[ \lim _{\mathbf{x} \rightarrow \mathbf{c}} f(\mathbf{x})=f(\mathbf{c}) . \]

Las siguientes propiedades básicas de límites se derivan inmediatamente de las propiedades análogas para límites de secuencias.

Proposición\(\PageIndex{1}\)

Supongamos\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\) y\(g: \mathbb{R}^{n} \rightarrow \mathbb{R}\) con

\[ \lim _{\mathbf{x} \rightarrow \mathbf{c}} f(\mathbf{x})=L \nonumber \]

y

\[ \lim _{\mathbf{x} \rightarrow \mathbf{c}} g(\mathbf{x})=M. \nonumber \]

Entonces

\ [\ begin {align}
\ lim _ {\ mathbf {x}\ fila derecha\ mathbf {c}} (f (\ mathbf {x}) +g (\ mathbf {x})) =L+M,\ etiqueta {3.1.6}
\\ lim _ {\ mathbf {x}\ fila derecha\ mathbf {c}} (f (\ mathbf {x}) -g (\ mathbf {x}) = L-M,\ etiqueta {3.1.7}\
\ lim _ {\ mathbf {x}\ fila derecha\ mathbf {c}} f (\ mathbf {x}) g (\ mathbf { x}) =L M,\ etiqueta {3.1.8}\
\ lim _ {\ mathbf {x}\ fila derecha\ mathrm {c}}\ frac {f (\ mathbf {x})} {g (\ mathbf {x})} =\ frac {L} {M},\ etiqueta {3.1.9}
\ end {align}\]

y

\[ \lim _{\mathbf{x} \rightarrow \mathbf{c}} k f(\mathbf{x})=k L \label{3.1.10} \]

para cualquier escalar\(k\).

Ahora supongamos\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\)\(h: \mathbb{R} \rightarrow \mathbb{R}\),

\[ \lim _{\mathbf{x} \rightarrow \mathbf{c}} f(\mathbf{x})=L , \]

y\(h\) es continuo en\(L\). Luego, para cualquier secuencia\(\left\{\mathbf{x}_{m}\right\}\) en\(\mathbb{R}^n\) con

\[ \lim _{m \rightarrow \infty} \mathbf{x}_{m}=\mathbf{c} , \]

tenemos

\[ \lim _{m \rightarrow \infty} f\left(\mathbf{x}_{m}\right)=L , \]

y así

\[ \lim _{m \rightarrow \infty} h\left(f\left(\mathbf{x}_{m}\right)\right)=h(L) \]

por la continuidad de\(h\) at\(L\). Así tenemos el siguiente resultado sobre composiciones de funciones.

Proposición\(\PageIndex{2}\)

Si\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\)\(h: \mathbb{R} \rightarrow \mathbb{R}\),

\[ \lim _{\mathbf{x} \rightarrow \mathbf{c}} f(\mathbf{x})=L , \nonumber \]

y\(h\) es continuo en\(L\), entonces

\[ \lim _{\mathbf{x} \rightarrow \mathbf{c}} h \circ f(\mathbf{x})=\lim _{\mathbf{x} \rightarrow \mathbf{c}} h(f(\mathbf{x}))=h(L) . \label{3.1.15} \]

Ejemplo\(\PageIndex{6}\)

Supongamos que definimos\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\) por

\[ f\left(x_{1}, x_{2}, \ldots, x_{n}\right)=x_{k} , \nonumber \]

donde\(k\) es un entero fijo entre 1 y\(n\). Si\(\mathbf{a}=\left(a_{1}, a_{2}, \ldots, a_{n}\right)\) es un punto en\(\mathbb{R}^n\) y\(\lim _{m \rightarrow \infty} \mathbf{x}_{m}=\mathbf{a}\), entonces

\[ \lim _{m \rightarrow \infty} f\left(\mathbf{x}_{m}\right)=\lim _{m \rightarrow \infty} x_{m k}=a_{k}, \nonumber \]

donde\(x_{mk}\) esta la coordenada\(k\) th de\(\mathbf{x}_m\). Así

\[ \lim _{\mathbf{x} \rightarrow \mathbf{a}} f(\mathbf{x})=a_{k} . \nonumber \]

Este resultado es un bloque de construcción básico para los ejemplos que siguen. Para un ejemplo particular, si\(f(x, y)=x,\) entonces

\[ \lim _{(x, y) \rightarrow(2,3)} f(x, y)=\lim _{(x, y) \rightarrow(2,3)} x=2 . \nonumber \]

Ejemplo\(\PageIndex{7}\)

Si definimos\(f: \mathbb{R}^{3} \rightarrow \mathbb{R}\) por

\[ f(x, y, z)=x y z , \nonumber \]

luego, usando (\(\ref{3.1.8}\)) en combinación con el ejemplo anterior,

\ begin {alineado}
\ lim _ {(x, y, z)\ fila derecha (a, b, c)} f (x, y, z) &=\ lim _ {(x, y, z)\ fila derecha (a, b, c)} x y z\\
&=\ izquierda (\ lim _ {(x, y, z)\ derecha (a, b, c)} x\ derecha)\ izquierda (\ lim _ {(x, y, z)\ fila derecha (a, b, c)} y\ derecha)\ izquierda (\ lim _ {(x, y, z)\ fila derecha (a, b, c)} z\ derecha )\\
&=a b c.
\ end {alineado}

para cualquier punto\((a,b,c)\) en\(\mathbb{R}^{3}\). Por ejemplo,

\[ \lim _{(x, y, z) \rightarrow(3,2,1)} f(x, y, z)=\lim _{(x, y, z) \rightarrow(3,2,1)} x y z=(3)(2)(1)=6 . \nonumber \]

Ejemplo\(\PageIndex{8}\)

Combinando los ejemplos anteriores con (\(\ref{3.1.6}\)\(\ref{3.1.7}\)), (\(\ref{3.1.8}\)), () y (\(\ref{3.1.10}\)), tenemos

\ begin {alineado}
\ lim _ {(x, y, z)\ fila derecha (2,1,3)}\ izquierda (x y^ {2} +3 x y z-6 x z\ derecha) =( &\ izquierda. \ lim _ {(x, y, z)\ fila derecha (2,1,3)} x\ derecha)\ izquierda (\ lim _ {(x, y, z)\ fila derecha (2,1,3)} y\ derecha)\ izquierda (\ lim _ {(x, y, z)\ fila derecha (2,1,3)} y\ derecha)\\
&+3\ izquierda (\ lim _ {(x, y, z)\ fila derecha (2,1,3)} x\ derecha)\ izquierda (\ lim _ {(x, y, z)\ fila derecha (2,1,3)} y\ derecha)\ izquierda (\ lim _ {(x, y, z)\ fila derecha (2,1, 3)} z\ derecha)\\
&-6\ izquierda (\ lim _ {(x, y, z)\ derecha (2,1,3)} x\ derecha)\ izquierda (\ lim _ {(x, y, z)\ derecha (2,1,3)} z\ derecha)\\
=& (2) (1) (1) (1) + (3) (2) (1) (3) - (6) (2) (3)\\
=&-16.
\ end {alineado}

Los tres últimos ejemplos son todos ejemplos de polinomios en varias variables. En general, una función\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\) de la forma

\[ f\left(x_{1}, x_{2}, \ldots, x_{n}\right)=a x_{1}^{i_{1}} x_{2}^{i_{2}} \cdots x_{n}^{i_{n}} , \nonumber \]

donde\(a\) es un escalar y\(i_{1}, i_{2}, \ldots, i_{n}\) son enteros no negativos, se llama monomio. Una función que es una suma de monomios se llama polinomio. La siguiente proposición es consecuencia de los ejemplos anteriores y (\(\ref{3.1.6}\)), (\(\ref{3.1.7}\)), (\(\ref{3.1.8}\)) y (\(\ref{3.1.10}\)).

Proposición\(\PageIndex{3}\)

Si\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\) es un polinomio, entonces para cualquier punto\(\mathbf{c}\) en\(\mathbb{R}^n\),

\[ \lim _{\mathbf{x} \rightarrow \mathbf{c}} f(\mathbf{x})=f(\mathbf{c}) . \]

En otras palabras,\(f\) es continuo en cada punto\(\mathbf{c}\) en\(\mathbb{R}^n\).

Si\(g\) y\(h\) son ambos polinomios, entonces llamamos a la función

\[ f(\mathbf{x})=\frac{g(\mathbf{x})}{h(\mathbf{x})} \]

una función racional. La proposición siguiente es consecuencia del teorema anterior y (\(\ref{3.1.9}\)).

Proposición\(\PageIndex{4}\)

Si\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\) es una función racional definida en\(\mathbf{c}\), entonces

\[ \lim _{\mathbf{x} \rightarrow \mathbf{c}} f(\mathbf{x})=f(\mathbf{c}) . \label{3.1.18} \]

En otras palabras,\(f\) es continuo en cada punto\(\mathbf{c}\) de su dominio.

Ejemplo\(\PageIndex{9}\)

Desde

\[ f(x, y, z)=\frac{x^{2} y+3 x y z^{2}}{4 x^{2}+3 z^{2}} \nonumber \]

es una función racional, tenemos, por ejemplo,

\[ \lim _{(x, y, z) \rightarrow(2,1,3)} f(x, y, z)=\lim _{(x, y, z) \rightarrow(2,1,3)} \frac{x^{2} y+3 x y z^{2}}{4 x^{2}+3 z^{2}}=\frac{4+54}{16+27}=\frac{58}{43} . \nonumber \]

Ejemplo\(\PageIndex{10}\)

Combinando (\(\ref{3.1.18}\)) con (\(\ref{3.1.15}\)), tenemos

\ [\ begin {alineado}
\ lim _ {(x, y, z)\ fila derecha (1,2,1)}\ log\ izquierda (\ frac {1} {x^ {2} +y^ {2} +z^ {2}}\ derecha) &=\ log\ izquierda (\ lim _ {(x, y, z)\ fila derecha (1,2,1)}\ frac {1} x^ {2} +y^ {2} +z^ {2}}\ derecha)\\
&=\ log\ izquierda (\ frac {1} {6}\ derecha)\\
&=-\ log (6).
\ end {alineado}\]

A partir de la continuidad de la función de raíz cuadrada y nuestro resultado anterior sobre la continuidad de los polinomios, podemos concluir que la función\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\) definida por

\[ f\left(x_{1}, x_{2}, \ldots, x_{n}\right)=\left\|\left(x_{1}, x_{2}, \ldots, x_{n}\right)\right\|=\sqrt{x_{1}^{2}+x_{2}^{2}+\cdots+x_{n}^{2}} \nonumber \]

es una función continua. Este hecho es útil para computar algunos límites, particularmente en combinación con el hecho de que para cualquier punto\(\mathbf{x}=\left(x_{1}, x_{2}, \ldots, x_{n}\right)\) en\(\mathbb{R}^n\),

\[ \|\mathbf{x}\|=\sqrt{x_{1}^{2}+x_{2}^{2}+\cdots+x_{n}^{2}} \geq \sqrt{x_{k}^{2}}=\left|x_{k}\right| \label{3.1.19} \]

para cualquier\(k=1,2, \ldots, n\).

Ejemplo\(\PageIndex{11}\)

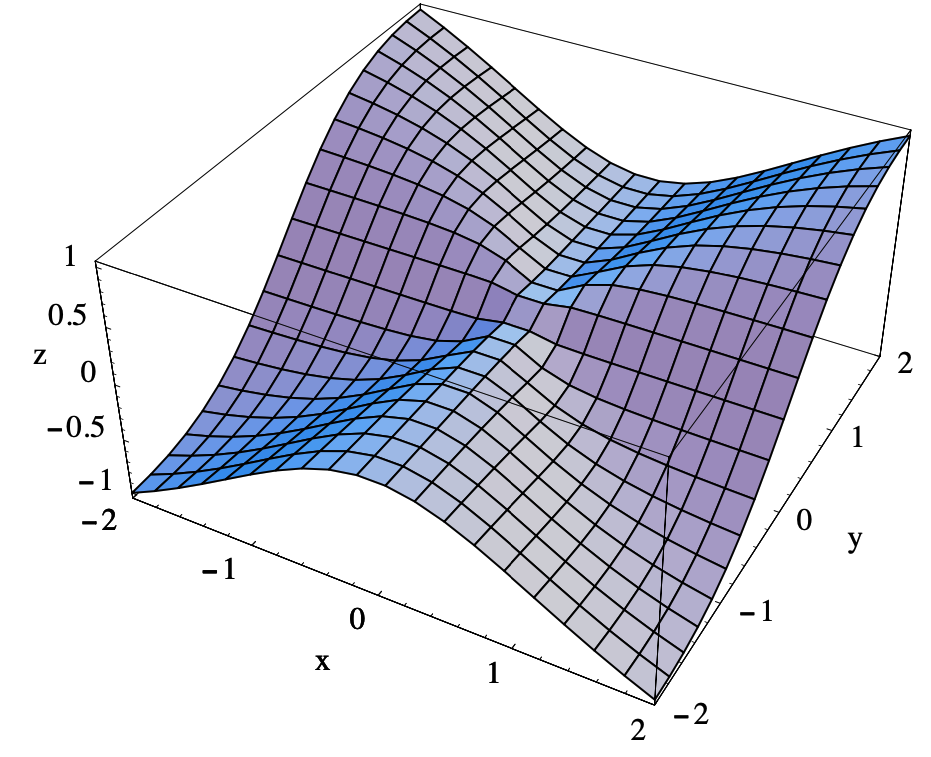
Supongamos que\(f: \mathbb{R}^{2} \rightarrow \mathbb{R}\) está definido por

\[ f(x, y)=\frac{x^{2} y}{x^{2}+y^{2}} . \nonumber \]

Aunque\(f\) es una función racional, no podemos usar (\(\ref{3.1.18}\)) para calcular

\[ \lim _{(x, y) \rightarrow(0,0)} f(x, y) \nonumber \]

ya que no\(f\) se define en (0, 0). Sin embargo, si dejamos\(\mathbf{x}=(x, y)\), entonces, usando (\(\ref{3.1.19}\)),

\[ |f(x, y)|=\left|\frac{x^{2} y}{x^{2}+y^{2}}\right|=\frac{|x|^{2}|y|}{\left|x^{2}+y^{2}\right|}=\frac{|x|^{2}|y|}{\|\mathbf{x}\|^{2}} \leq \frac{\|\mathbf{x}\|^{2}\|\mathbf{x}\|}{\|\mathbf{x}\|^{2}}=\|\mathbf{x}\| . \nonumber \]

Ahora

\[ \lim _{(x, y) \rightarrow(0,0)}\|\mathbf{x}\|=0 , \nonumber \]

por lo

\[ \lim _{(x, y) \rightarrow(0,0)}|f(x, y)|=0 . \nonumber \]

De ahí

\[ \lim _{(x, y) \rightarrow(0,0)} f(x, y)=\lim _{(x, y) \rightarrow(0,0)} \frac{x^{2} y}{x^{2}+y^{2}}=0 . \nonumber \]

Ver Figura 3.1.6.

Figura\(\PageIndex{6}\): Gráfica de\(f(x, y)=\frac{x^{2} y}{x^{2}+y^{2}}\)

Recordemos que para una función\(\varphi: \mathbb{R} \rightarrow \mathbb{R}\),

\[ \lim _{t \rightarrow c} \varphi(t)=L \nonumber \]

si y solo si ambos

\[ \lim _{t \rightarrow c^{-}} \varphi(t)=L \nonumber \]

y

\[ \lim _{t \rightarrow c^{+}} \varphi(t)=L . \nonumber \]

En particular, si los límites unilaterales no coinciden, podemos concluir que el límite no existe. Se puede aplicar un razonamiento similar a una función\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\), siendo la diferencia que hay infinitamente muchas curvas diferentes a lo largo de las cuales la variable\(\mathbf{x}\) podría acercarse a un punto dado\(\mathbf{c}\) en\(\mathbb{R}^n\), a diferencia de solo las dos direcciones de enfoque en \(\mathbb{R}\). En consecuencia, no es posible establecer la existencia de un límite con este tipo de argumentos. Sin embargo, encontrar dos formas de abordaje\(\mathbf{c}\) que produzcan diferentes valores limitantes es suficiente para demostrar que el límite no existe.

Ejemplo\(\PageIndex{12}\)

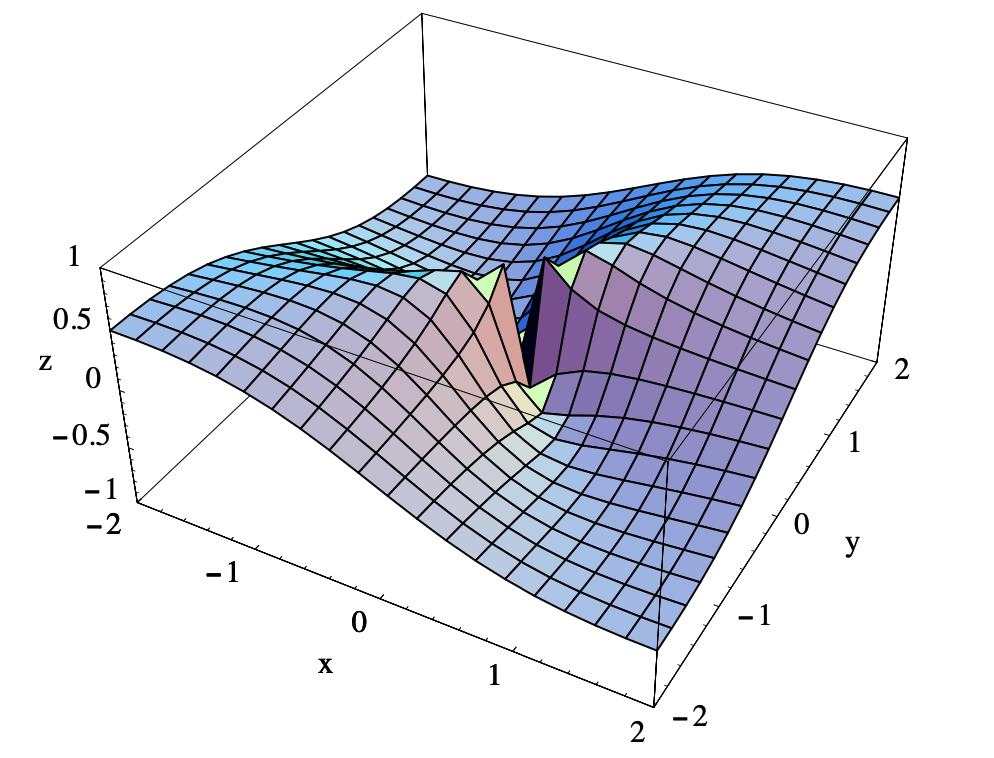
Supongamos que\(g: \mathbb{R}^{2} \rightarrow \mathbb{R}\) está definido por

\[ g(x, y)=\frac{x y}{x^{2}+y^{2}} . \nonumber \]

Si definimos\(\alpha: \mathbb{R}^{2} \rightarrow \mathbb{R}\) por\(\alpha(t)=(t, 0)\), entonces

\[ \lim _{t \rightarrow 0} \alpha(t)=\lim _{t \rightarrow 0}(t, 0)=(0,0) \nonumber \]

y

\[ \lim _{t \rightarrow 0} g(\alpha(t))=\lim _{t \rightarrow 0} f(t, 0)=\lim _{t \rightarrow 0} \frac{0}{t^{2}}=0 . \nonumber \]

Ahora\(\alpha\) es una parametrización del\(x\) eje -eje, por lo que el cálculo de límite anterior dice que\(g(x,y)\) se acerca a 0 como\((x,y)\) enfoques (0, 0) a lo largo del\(x\) eje -eje. Sin embargo, si definimos\(\beta: \mathbb{R} \rightarrow \mathbb{R}^{2}\) por\(\beta(t)=(t, t)\), entonces\(\beta\) parametriza la línea\(x=y\),

\[ \lim _{t \rightarrow 0} \beta(t)=\lim _{t \rightarrow 0}(t, t)=(0,0) , \nonumber \]

y

\[ \lim _{t \rightarrow 0} g(\beta(t))=\lim _{t \rightarrow 0} f(t, t)=\lim _{t \rightarrow 0} \frac{t^{2}}{2 t^{2}}=\frac{1}{2} . \nonumber \]

De ahí\(g(x,y)\) se aproxima\(\frac{1}{2}\) como\((x,y)\) enfoques (0, 0) a lo largo de la línea\(x=y\). Dado que estos dos límites son diferentes, podemos concluir que\(g(x,y)\) no tiene un límite como\((x,y)\) enfoques (0, 0). Obsérvese que\(g\) \(f\)en este ejemplo y en el ejemplo anterior son funciones muy similares, aunque nuestros cálculos de límite muestran que su comportamiento alrededor (0, 0) difiere significativamente. En particular,\(f\) tiene un límite como\((x,y)\) aproximaciones (0, 0), mientras que\(g\) no. Esto puede ser

visto comparando la gráfica de\(g\) la Figura 3.1.7, que tiene un desgarro en el origen, con la de la\(f\) Figura 3.1.6.

Figura\(\PageIndex{7}\): Gráfica de\(g(x, y)=\frac{x y}{x^{2}+y^{2}}\)

La siguiente proposición enumera algunas propiedades básicas de las funciones continuas, todas las cuales siguen inmediatamente de la lista similar de propiedades de límites.

Proposición\(\PageIndex{5}\)

Supongamos\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\) y ambos\(g: \mathbb{R}^{n} \rightarrow \mathbb{R}\) son continuos en\(\mathbf{c}\). Luego las funciones con valores\(\mathbf{x}\) dados por

\ [\ begin {align}
f (\ mathbf {x}) +g (\ mathbf {x}),\ label {3.1.20}\\
f (\ mathbf {x}) -g (\ mathbf {x}),\ label {3.1.21}\\
f (\ mathbf {x}) g (\ mathbf {x}),\ etiqueta {3.1.22}\
\ frac {f (\ mathbf {x})} {g (\ mathbf {x})}\ label {3.1.23}
\ end {align}\]

(proporcionado\(g(\mathbf{c}) \neq 0\)), y

\[ k f(\mathbf{x}), \label{3.1.24} \]

donde\(k\) es cualquier escalar, son todos continuos en\(\mathbf{c}\).

Del resultado anterior sobre el límite de una composición de dos funciones, tenemos la siguiente proposición.

Proposición\(\PageIndex{6}\)

Si\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\) es continuo en\(\mathbf{c}\) y\(\varphi: \mathbb{R} \rightarrow \mathbb{R}\) es continuo en\(f(\mathbf{c})\), entonces\(\varphi \circ f\) es continuo en\(\mathbf{c}\).

Ejemplo\(\PageIndex{13}\)

Dado que la función\(\varphi(t)=\sin (t)\) es continua para todos\(t\) y la función

\[ f(x, y, z)=\sqrt{x^{2}+y^{2}+z^{2}} \nonumber \]

es continuo en todos los puntos\((x,y,z)\) en\(\mathbb{R}^3\), la función

\[ g(x, y, z)=\sin \left(\sqrt{x^{2}+y^{2}+z^{2}}\right) \nonumber \]

es continuo en todos los puntos\((x,y,z)\) en\(\mathbb{R}^3\).

Ejemplo\(\PageIndex{14}\)

Dado que la función

\[ h(x, y)=\sin \left(\sqrt{x^{2}+y^{2}}\right) \nonumber \]

es continuo para all\((x,y)\) in\(\mathbb{R}^2\) (mismo argumento que en el ejemplo anterior) y la función

\[ g(x, y)=\sqrt{x^{2}+y^{2}} \nonumber \]

es continuo para todos\((x,y)\) en\(\mathbb{R}^2\), la función

\[ f(x, y)=\frac{\sin \left(\sqrt{x^{2}+y^{2}}\right)}{\sqrt{x^{2}+y^{2}}} \nonumber \]

es, usando (\(\ref{3.1.23}\)), continuo en cada punto\((x, y) \neq(0,0)\) de\(\mathbb{R}^{2}\). Además, si dejamos\(\mathbf{x}=(x, y)\), entonces

\[ \lim _{(x, y) \rightarrow(0,0)} f(x, y)=\lim _{(x, y) \rightarrow(0,0)} \frac{\sin \left(\sqrt{x^{2}+y^{2}}\right)}{\sqrt{x^{2}+y^{2}}}=\lim _{(x, y) \rightarrow(0,0)} \frac{\sin (\|\mathbf{x}\|)}{\|\mathbf{x}\|}=\lim _{r \rightarrow 0} \frac{\sin (r)}{r}=1 . \nonumber \]

De ahí que la discontinuidad en (0, 0) sea removible. Es decir, si definimos

\[ g(x, y)= \begin{cases}\frac{\sin \left(\sqrt{x^{2}+y^{2}}\right)}{\sqrt{x^{2}+y^{2}}}, & \text { if }(x, y) \neq(0,0), \\ 1, & \text { if }(x, y)=(0,0),\end{cases} \nonumber \]

entonces\(g\) es continuo para todos\((x,y)\) en\(\mathbb{R}^2\).

Conjuntos abiertos y cerrados

En el cálculo de una sola variable se habla de que una función es continua no sólo en un punto, sino en un intervalo abierto, es decir, que la función es continua en cada punto del intervalo abierto. De igual manera, necesitamos generalizar la definición de continuidad de una función\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\) desde la de continuidad en un punto de entrada\(\mathbb{R}^n\) hasta la idea de que una función sea continua en un set in\(\mathbb{R}^n\). Ahora la condición para que una función\(f\) sea continua en un punto\(\mathbf{c}\) requiere que\(f\) se defina en alguna bola abierta que contenga\(\mathbf{c}\). De ahí que para decir que\(f\) es continuo en cada punto de algún conjunto\(U\), es necesario que, dado cualquier punto\(\mathbf{u}\) en\(U\),\(f\) se defina sobre alguna bola abierta que contenga\(\mathbf{u}\). Esto proporciona la motivación para la siguiente definición.

Definición\(\PageIndex{5}\)

Decimos que un conjunto de puntos\(U\) en\(\mathbb{R}^n\) está abierto si cada vez que\(\mathbf{u}\) es un punto en\(U\), existe un número real\(r>0\) tal que la bola abierta\(B^{n}(\mathbf{u}, r)\) se encuentra enteramente dentro\(U\). Decimos que un conjunto de puntos\(C\) en\(\mathbb{R}^n\) está cerrado si el conjunto de todos los puntos en los\(\mathbb{R}^n\) que no se encuentran en\(C\) forma un conjunto abierto.

Ejemplo\(\PageIndex{15}\)

\(\mathbb{R}^n\)es en sí mismo un conjunto abierto.

Ejemplo\(\PageIndex{16}\)

Cualquier bola abierta en\(\mathbb{R}^n\) es un conjunto abierto. En particular, cualquier intervalo abierto en\(\mathbb{R}\) es un conjunto abierto. Para ver por qué, considera una pelota abierta\(B^{n}(\mathbf{a}, r)\) en\(\mathbb{R}^n\). Dado un punto\(\mathbf{y}\) adentro\(B^{n}(\mathbf{a}, r)\), deja\(s\) ser el menor de\(\|\mathbf{y}-\mathbf{a}\|\) (la distancia desde\(\mathbf{y}\) el centro de la pelota) y\(r-\|\mathbf{y}-\mathbf{a}\|\) (la distancia desde\(\mathbf{y}\) hasta el borde de la pelota). Entonces\(B^{n}(\mathbf{y}, s)\) es una bola abierta que yace completamente dentro\(B^{n}(\mathbf{a}, r)\). De ahí\(B^{n}(\mathbf{a}, r)\) que sea un conjunto abierto.

Ejemplo\(\PageIndex{17}\)

Cualquier bola cerrada\(\mathbb{R}^n\) es un conjunto cerrado. En particular, cualquier intervalo cerrado en\(\mathbb{R}\) es un conjunto cerrado. Para ver por qué, considera una bola cerrada\(\bar{B}^{n}(\mathbf{a}, r)\). Dado un punto\(\mathbf{y}\) no en\(\bar{B}^{n}(\mathbf{a}, r)\), vamos\(s=\|\mathbf{y}-\mathbf{a}\|-r\), la distancia desde\(\mathbf{y}\) hasta el borde de\(\bar{B}^{n}(\mathbf{a}, r)\). Entonces\(B^{n}(\mathbf{y}, s)\) es una bola abierta que yace completamente fuera de\(\bar{B}^{n}(\mathbf{x}, r)\). De ahí\(\bar{B}^{n}(\mathbf{x}, r)\) que sea un conjunto cerrado.

Ejemplo\(\PageIndex{18}\)

Dados los números reales\(a_{1}<b_{1}, a_{2}<b_{2}, \ldots, a_{n}<b_{n}\), llamamos al conjunto

\[ U=\left\{\left(x_{1}, x_{2}, \ldots, x_{n}\right): a_{i}<x_{i}<b_{i}, i=1,2, \ldots, n\right\} \nonumber \]

un rectángulo abierto en\(\mathbb{R}^n\) y el conjunto

\[ C=\left\{\left(x_{1}, x_{2}, \ldots, x_{n}\right): a_{i} \leq x_{i} \leq b_{i}, i=1,2, \ldots, n\right\} \nonumber \]

un rectángulo cerrado en\(\mathbb{R}^n\). Un argumento similar al del ejemplo anterior muestra que\(U\) es un conjunto abierto y\(C\) es un conjunto cerrado.

Definición\(\PageIndex{6}\)

Decimos que una función\(f: \mathbb{R}^{n} \rightarrow \mathbb{R}\) es continua en un conjunto abierto\(U\) si\(f\) es continua en cada punto\(u\) de\(U\).

Ejemplo\(\PageIndex{19}\)

La función

\[ f(x, y, z)=\frac{3 x y z-6 x}{x^{2}+y^{2}+z^{2}+1} \nonumber \]

es continuo en\(\mathbb{R}^3\).

Ejemplo\(\PageIndex{20}\)

Las funciones

\[ f(x, y)= \begin{cases}\frac{x^{2} y}{x^{2}+y^{2}}, & \text { if }(x, y) \neq(0,0), \\ 0, & \text { if }(x, y)=(0,0), \end{cases} \nonumber \]

y

\[ g(x, y)= \begin{cases}\frac{\sin \left(\sqrt{x^{2}+y^{2}}\right)}{\sqrt{x^{2}+y^{2}}}, & \text { if }(x, y) \neq(0,0), \\ 1, & \text { if }(x, y)=(0,0),\end{cases} \nonumber \]

son, a partir de nuestro trabajo en ejemplos anteriores, continuos\(\mathbb{R}^2\).

Ejemplo\(\PageIndex{21}\)

La función

\[ g(x, y)=\frac{x y}{x^{2}+y^{2}} \nonumber \]

es continuo en el set abierto

\[ U=\big\{(x, y):(x, y) \neq(0,0)\big\}. \nonumber \]

Nótese que en este caso no es posible definir\(g\)\((0,0)\) en de tal manera que la función resultante sea continua a\((0,0),\) consecuencia de nuestro trabajo anterior mostrando que\(g\) no tiene un límite como\((x,y)\) enfoques\((0,0).\)

Ejemplo\(\PageIndex{22}\)

La función

\[ f(x, y)=\log (x y) \nonumber \]

es continuo en el set abierto

\[ U=\big\{(x, y): x>0 \text { and } y>0\big\}. \nonumber \]