3.3: Lemas del mismo signo

Última actualización
Guardar como PDF

Page ID: 114419

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Lema$\PageIndex{1}$

Asumir$Q' \in [PQ)$ y$Q' \ne P$. Entonces para cualquiera$X \in (PQ)$ los ángulos$PQX$ y$PQ'X$ tienen el mismo signo.

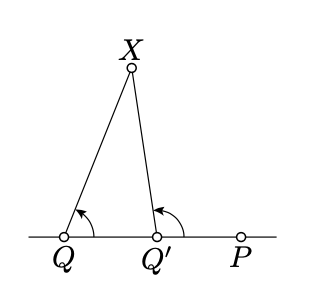
$2021-02-02 1.37.17.png$

Prueba

Por la Proposición 2.2.2, para cualquiera$t \in [0, 1]$ hay un punto único$Q_t \in [PQ)$ tal que

\[PQ_t = (1 - t) \cdot PQ + t \cdot PQ'.\]

Tenga en cuenta que el mapa$t \mapsto Q_t$ es continuo,

$Q_0 = Q$,$Q_1 = Q'$

y para cualquiera$t \in [0, 1]$, tenemos eso$P \ne Q_t$.

Aplicando Corolario 3.2.1$P_t = P$, para$Q_t$,$X_t = X$, y, obtenemos que$\angle PQX$ tiene el mismo signo que$\angle PQ'X$.

Teorema$\PageIndex{1}$ Signs of angles of a triangle

En triángulo arbitrario no degenerado$ABC$, los ángulos$ABC, BCA,$ y$CAB$ tienen el mismo signo.

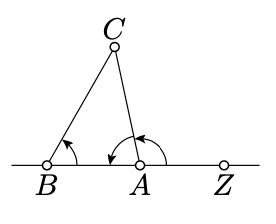
$2021-02-02 1.7.20.png$

Prueba

Elige un punto$Z \in (AB)$ para que$A$ se encuentre entre$B$ y$Z$.

Según Lemma$\PageIndex{1}$, los ángulos$ZBC$ y$ZAC$ tienen el mismo signo.

Tenga en cuenta que$\measuredangle ABC = \measuredangle ZBC$ y

\[\measuredangle ZAC + \measuredangle CAB \equiv \pi.\]

Por lo tanto,$\angle CAB$ tiene el mismo signo$\angle ZAC$ que el que a su vez tiene el mismo signo que$\measuredangle ABC = \measuredangle ZBC$.

Repetiendo el mismo argumento para$\angle BCA$ y$\angle CAB$, obtenemos el resultado.

Lema$\PageIndex{2}$

Supongamos que$[XY]$ no se cruza$(PQ)$, entonces los ángulos$PQX$ y$PQY$ tienen el mismo signo.

La prueba es casi idéntica a la anterior.

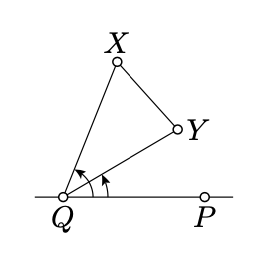
$2021-02-02 1.52.14.png$

Prueba

De acuerdo con la Proposición 2.2.2, para cualquiera$t \in [0, 1]$ hay un punto$X_t \in [XY]$, tal que

$XX_t = t \cdot XY.$

Tenga en cuenta que el mapa$t \mapsto X_t$ es continuo. Por otra parte$X_0 = X$,$X_1 = Y$,, y$X_t \not\in (QP)$ para cualquier$t \in [0, 1]$.

Aplicando Corolario 3.2.1$P_t = P$, para$Q_t = Q$,$X_t$, y, obtenemos que$\angle PQX$ tiene el mismo signo que$\angle PQY$.

Lema\(\PageIndex{1}\)

Teorema\(\PageIndex{1}\) Signs of angles of a triangle

Lema\(\PageIndex{2}\)