3.2: Teorema del Valor Intermedio

Última actualización
Guardar como PDF

Page ID: 114420

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Teorema$\PageIndex{1}$ Intermediate value theorem

Dejar$f: [a, b] \to \mathbb{R}$ ser una función continua. Asumir$f(a)$ y$f(b)$ tener signos opuestos, entonces$f(t_0) = 0$ para algunos$t_0 \in [a,b]$.

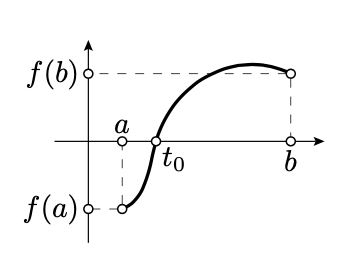
$2021-02-02 11.00.07.png$

Se supone que el teorema del valor intermedio es conocido; debe ser cubierto en cualquier curso de cálculo. Usaremos solo el siguiente corolario:

Corolario$\PageIndex{1}$

Supongamos que para cualquiera$t \in [0, 1]$ tenemos tres puntos en el plano$O_t$,$A_t$, y$B_t$, tal que

Cada función$t \mapsto O_t$,$t \mapsto A_t$, y$t \mapsto B_t$ es continua.
Para cualquiera$t \in [0, 1]$, los puntos$O_t, A_t$, y$B_t$ no se encuentran en una línea. Entonces$\angle A_0 O_0 B_0$ y$\angle A_1 O_1 B_1$ tener la misma señal.

Prueba

Considera la función$f(t) = \measuredangle A_tO_tB_t$.

Dado que los puntos$O_t, A_t$, y$B_t$ no se alinean en una línea, el Teorema 2.4.1 implica que$f(t) = \measuredangle A_tO_tB_t \ne 0$ ni$\pi$ para ninguna$t \in [0, 1]$.

Por lo tanto, por Axioma IIIc y Ejercicio 1.9.2,$f$ es una función continua. Por el teorema del valor intermedio,$f(0)$ y$f(1)$ tienen el mismo signo; de ahí sigue el resultado.