3.4: Medioplanos

Última actualización
Guardar como PDF

Page ID: 114415

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Proposición$\PageIndex{1}$

Asumir$X, Y \not\in (PQ)$. Entonces los ángulos$PQX$ y$PQY$ tienen el mismo signo si y sólo si$[XY]$ no se interseca$(PQ)$.

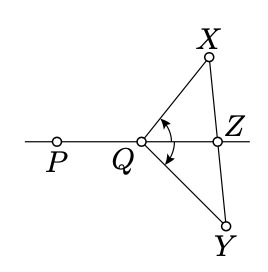
$2021-02-02 1.56.57.png$

Prueba

El if-part se desprende de Lemma 3.3.2.

Asumir$[XY]$ cruces$(PQ)$; supongamos que eso$Z$ denota el punto de intersección. Sin pérdida de generalidad, podemos asumir$Z \ne P$.

Tenga en cuenta que$Z$ se encuentra entre$X$ y$Y$. Según Lemma 3.1.1,$\angle PZX$ y$\angle PZY$ tienen signos opuestos. Se prueba la declaración si$Z = Q$.

Si$Z \ne Q$, entonces$\angle ZQX$ y$QZX$ tener signos opuestos por 3.7. De la misma manera lo conseguimos$\angle ZQY$ y$\angle QZY$ tenemos signos opuestos.

Si$Q$ yace entre$Z$ y$P$, entonces por Lema 3.1.1 dos pares de ángulos$\angle PQX$,$\angle ZQX$ y$\angle PQY$,$\angle ZQY$ tienen signos opuestos. De ello se deduce$\angle PQX$ y$\angle PQY$ tienen signos opuestos según se requiera.

En el caso restante$[QZ) = [QP)$ y por tanto$\angle PQX = \angle ZQX$ y$\angle PQY = \angle ZQY$. Por lo tanto nuevamente$\angle PQX$ y$\angle PQY$ tener signos opuestos según se requiera.

Corolario$\PageIndex{1}$

El complemento de una línea$(PQ)$ en el plano se puede presentar de una manera única como una unión de dos subconjuntos disgregados llamados medios planos de tal manera que

(a) Dos puntos$X, Y \not\in (PQ)$ se encuentran en el mismo medio plano si y sólo si los ángulos$PQX$ y$PQY$ tienen el mismo signo.

b) Dos puntos$X, Y \not\in (PQ)$ en un mismo semiplano si y sólo si$[XY]$ no se intersectan$(PQ)$.

Decimos eso$X$ y nos$Y$ acostamos a un lado de$(PQ)$ si se encuentran en uno de los medios planos de$(PQ)$ y decimos eso$P$ y se$Q$ encuentran en los lados opuestos de$l$ si se encuentran en los diferentes medios planos de$l$.

Ejercicio$\PageIndex{1}$

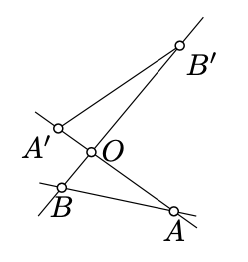
Supongamos que los ángulos$AOB$ y$A'OB'$ son verticales y$B \not\in (OA)$. Mostrar que la línea$(AB)$ no se cruza con el segmento$[A'B']$.

$2021-02-02 2.07.49.png$

Pista: Tenga en cuenta que$O$ y$A'$ se encuentran en el mismo lado de$(AB)$. Análogamente$O$ y$B'$ se encuentran en el mismo lado de$(AB)$. De ahí el resultado.

Considera el triángulo$ABC$. Los segmentos$[AB], [BC]$, y$[CA]$ se llaman lados del triángulo.

Teorema$\PageIndex{1}$ Pasch's theorem

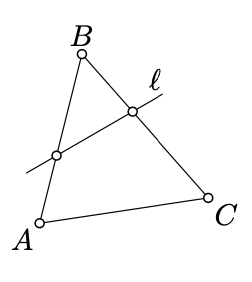
Supongamos que la línea$l$ no pasa a través de ningún vértice de un triángulo. Entonces se cruza con dos o cero lados del triángulo.

$2021-02-02 2.14.00.png$

Prueba

Supongamos que la línea$l$ se cruza con lado$[AB]$ del triángulo$ABC$ y no pasa a través$A, B,$ y$C$.

Por Corolario$\PageIndex{1}$, los vértices$A$ y se$B$ encuentran en lados opuestos de$l$.

El vértice$C$ puede estar en el mismo lado con$A$ y en el lado opuesto con$B$ o al revés. Por Corolario$\PageIndex{1}$, en el primer caso,$l$ se cruza de lado$[BC]$ y no se cruza$[AC]$; en el segundo caso,$l$ se cruza de lado$[AC]$ y no se cruza$[BC]$. De ahí sigue el enunciado.

Ejercicio$\PageIndex{2}$

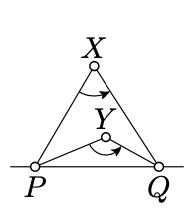
Mostrar que dos puntos$X, Y \not\in (PQ)$ se encuentran en el mismo lado de$(PQ)$ si y sólo si los ángulos$PXQ$ y$PYQ$ tienen el mismo signo.

$2021-02-02 2.15.16.png$

Pista: Aplicar el Teorema 3.3.1 para$\triangle PQX$$\triangle PQY$ y luego aplicar Corolario$\PageIndex{1}$a.

Ejercicio$\PageIndex{3}$

Dejar$\triangle ABC$ ser un triángulo no degenerado,$A' \in [BC]$ y$B' \in [AC]$. Mostrar que los segmentos$[AA']$ y se$[BB']$ cruzan.

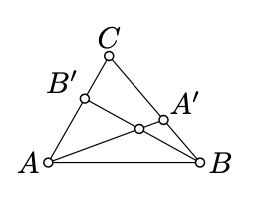
$2021-02-02 2.16.32.png$

Pista

Podemos suponer eso$A' \ne B, C$ y$B' \ne A, C$; de lo contrario la declaración se sostiene trivialmente.

Tenga en cuenta que$(BB')$ no se cruza$[A'C]$. Aplicando el teorema de Pasch (Teorema 3.4.1) para$\triangle AA'C$ y$(BB')$, obtenemos que los$(BB')$ intersets$[AA']$; denotan el punto de intersección por$M$.

De la misma manera conseguimos que$(AA')$ se cruza$[BB']$; es decir$M$ mentiras sobre$[AA']$ y$[BB']$.

Ejercicio$\PageIndex{4}$

Supongamos que los puntos$X$ y$Y$ se encuentran en lados opuestos de la línea$(PQ)$. Demuestre que la media línea$[PX)$ no se cruza$[QY)$.

Pista

Supongamos que$Z$ es el punto de intersección.

Tenga en cuenta que$Z \ne P$ y$Z \ne Q$. Por lo tanto,$Z \in (PQ)$.

$Z$Demuéstralo y$X$ acuéstate a un lado de$(PQ)$. Repite el argumento para mostrar eso$Z$ y$Y$ mentir a un lado de$(PQ)$. De ello se deduce$X$ y se$Y$ encuentran del mismo lado de$(PQ)$ - una contradicción.

Ejercicio Avanzado$\PageIndex{1}$

Tenga en cuenta que la siguiente cantidad

\[^{~} \measuredangle ABC = \begin{cases} \pi & \text{if } \measuredangle ABC = \pi \\ -\measuredangle ABC & \text{if } \measuredangle ABC < \pi \end{cases}\]

puede servir como la medida del ángulo; es decir, los axiomas se mantienen si uno$\measuredangle$ intercambia a$^{~} \measuredangle$ todas partes.

Demuestre eso$\measuredangle$ y$^{~} \measuredangle$ son las únicas medidas de ángulo posibles en el plano.
Demuestre que sin Axioma IIIc, esto ya no es cierto.

Proposición\(\PageIndex{1}\)

Corolario\(\PageIndex{1}\)

Teorema\(\PageIndex{1}\) Pasch's theorem