3.5: Triángulo con los lados dados

Última actualización
Guardar como PDF

Page ID: 114424

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Considera el triángulo$ABC$. Set

$a = BC$,$b = CA$,$c = AB.$

Sin pérdida de generalidad, podemos suponer que

$a \le b \le c.$

Entonces las tres desigualdades triangulares para$\triangle ABC$ mantener si y solo si

$c \le a + b$.

El siguiente teorema afirma que esta es la única restricción sobre$a$,$b$, y$c$.

Teorema$\PageIndex{1}$

Asumir eso$0 < a \le b \le c \le a + b$. Entonces hay un triángulo con lados$a, b$, y$c$; es decir, hay$\triangle ABC$ tal que$a = BC$,$b = CA$, y$c = AB$.

Prueba

Fijar los puntos$A$ y$B$ tal que$AB = c$. Dado$\beta \in [0, \pi]$, supongamos que$C_{\beta}$ denota el punto en el plano tal que$BC_{\beta} = a$ y$\measuredangle ABC = \beta$.

Según el Corolario$\PageIndex{1}$, el mapa$\beta \mapsto C_{\beta}$ es continuo. Por lo tanto, la función$b(\beta) = AC_{\beta}$ es continuada (formalmente, se desprende del Ejercicio 1.9.1 y del Ejercicio 1.9.2).

Tenga en cuenta que$b(0) = c - a$ y$b (\pi) = c + a$. Ya que$c - a \le b \le c + a$, por el teorema del valor intermedio (Teorema 3.2.1) existe$\beta_0 \in [0, \pi]$ tal que$b(\beta_0) = b$, de ahí el resultado.

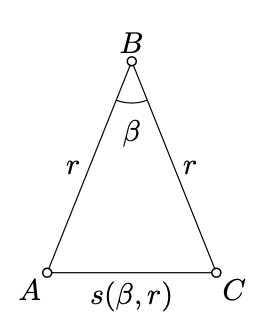
$2021-02-02 2.42.36.png$

Asumir$r > 0$ y$\pi > \beta > 0$. Considera el triángulo$ABC$ tal que$AB = BC = r$ y$\measuredangle ABC = \beta$. La existencia de tal triángulo se desprende del Axioma IIIa y de la Proposición 2.2.2.

Obsérvese que según Axioma IV, los valores$\beta$ y$r$ definen el triángulo$ABC$ hasta la congruencia. En particular, la distancia$AC$ depende sólo de$\beta$ y$r$.

\[s(\beta, r):= AC.\]

Proposición$\PageIndex{1}$

Dado$r > 0$ y$\varepsilon > 0$, hay$\delta > 0$ tal que

$0 < \beta < \delta \Rightarrow s(r, \beta) < \varepsilon.$

Prueba

Fijar dos puntos$A$ y$B$ tal que$AB = r$.

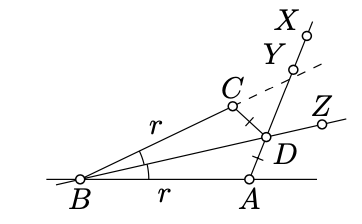
$2021-02-02 2.47.27.png$

Elija un punto$X$ tal que$AY = \dfrac{\varepsilon}{2}$; exista por la Proposición 2.2.2.

Tenga en cuenta que$X$ y$Y$ se encuentran en el mismo lado de$(AB)$; por lo tanto,$\angle ABY$ es positivo. Set$\delta = \measuredangle ABY$.

Supongamos$0 < \beta < \delta$; por Axioma IIIa, podemos elegir$B$ para que$\measuredangle ABC = \beta$ y$BC = r$. Además podemos elegir una media línea$[BZ)$ tal que$\measuredangle ABZ = \dfrac{1}{2} \cdot \beta$.

Tenga en cuenta que$A$ y se$Y$ encuentran en lados opuestos de$(BZ)$ y además$\measuredangle ABZ \equiv - \measuredangle CBZ$. En particular,$(BZ)$ se cruza$[AY]$; denota por$D$ el punto de intersección.

Ya que$D$ se encuentra entre$A$ y$Y$, tenemos eso$AD < AY$.

Ya que$D$ se encuentra en eso$(BZ)$ tenemos$\measuredangle ABD \equiv \measuredangle CBD$. Por Axioma IV,$\triangle ABD \cong \triangle CBD$. De ello se deduce que

\[\begin{array} {rcl} {s(r, \beta)} & = & {AC \le} \\ {} & \le & {AD + DC =} \\ {} & = & {2 \cdot AD <} \\ {} & < & {2 \cdot AY =} \\ {} & = & {\varepsilon} \end{array}\]

Corolario$\PageIndex{1}$

Fijar un número real$r > 0$ y dos puntos distintos$A$ y$B$. Entonces para cualquier número real$\beta \in [0, \pi]$, hay un punto único$C_{\beta}$ tal que$BC_{\beta} = r$ y$\measuredangle ABC_{\beta} = \beta$. Además,$\beta \mapsto C_{\beta}$ es un mapa continuo desde$[0, \pi]$ el plano.

Prueba

La existencia y singularidad de lo que$C_{\beta}$ se desprende del Axioma IIIa y de la Proposición 2.2.2.

Nota taht si$\beta_1 \ne \beta_2$, entonces

\[C_{\beta_1} C_{\beta_2} = s(r, |\beta_1 - \beta_2|).\]

Por Proposición$\PageIndex{1}$, el mapa$\beta \mapsto C_{\beta}$ es continuo.

Dado un número real positivo$r$ y una pinta$O$, el conjunto$\Gamma$ de todos los puntos en la distancia$r$ desde$O$ se llama círculo con radio$r$ y centro$O$.

Ejercicio$\PageIndex{1}$

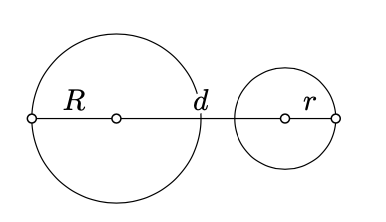
Mostrar que dos círculos se cruzan si y solo si

\[|R - r| \le d \le R + r,\]

donde$R$ y$r$ denotan sus radios, y$d$ — la distancia entre sus centros.

$2021-02-02 2.58.20.png$

Insinuación: La parte “solo si” se desprende de la desigualdad triangular. Para probar “si” parte, observar que Teorema$\PageIndex{1}$ implica la existencia de un triángulo con lados$r_1$,$r_2$, y$d$. Usa este triángulo para mostrar que hay un punto$X$ tal que$O_1X = r_1$ y$O_2X = r_2$, donde$O_1$ y$O_2$ son los centros de los círculos correspondientes.

Teorema\(\PageIndex{1}\)

Proposición\(\PageIndex{1}\)

Corolario\(\PageIndex{1}\)