5.3: Unicidad de una perpendicular

Última actualización
Guardar como PDF

Page ID: 114818

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Teorema$\PageIndex{1}$

Hay una y sólo una línea que pasa a través de un punto dado$P$ y es perpendicular a una línea dada$\ell$.

Según el teorema anterior, hay un punto único$Q \in \ell$ tal que$(QP) \perp \ell$. A este punto$Q$ se le llama el punto del pie de$P$ on$\ell$.

Prueba

Si$P \in \ell$, entonces tanto la existencia como la singularidad siguen de Axioma III.

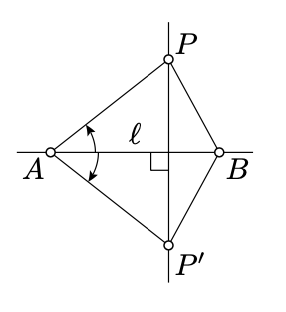
$2021-02-04 9.20.39.png$

Existencia para$P \not\in \ell$. Dejar$A$ y$B$ ser dos puntos distintos de$\ell$. Elige$P'$ para que$AP' = AP$ y$\meauredangle BAP' \equiv - \measuredangle BAP$. Según Axioma IV,$\triangle AP'B \cong \triangle APB$. En particular,$AP = AP'$ y$BP = BP'$.

Según el Teorema 5.2.1,$A$ y se$B$ encuentran sobre la bisectriz perpendicular a$[PP']$. En particular,$(PP') \perp (AB) = \ell$.

Singularidad para$P \not\in \ell$. Desde arriba podemos elegir un punto de tal$P'$ manera que$\ell$ forme la bisectriz perpendicular a$[PP']$.

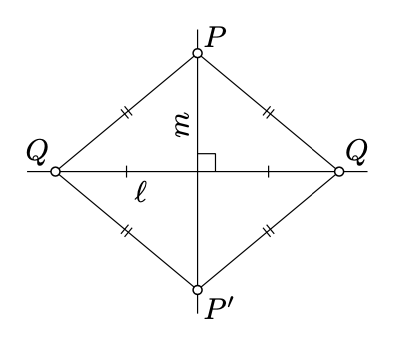
$2021-02-04 9.28.00.png$

Asumir$m \perp \ell$ y$P \in m$. Entonces$m$ es una bisectriz perpendicular a algún segmento$[QQ']$ de$\ell$; en particular,$PQ = PQ'$.

Ya que$\ell$ es la bisectriz perpendicular a$[PP']$, obtenemos eso$PQ = P'Q$ y$PQ' = P'Q'$. Por lo tanto,

$P'Q = PQ = PQ' = P'Q'$.

Por Teorema 5.2.1,$P'$ se encuentra sobre la bisectriz perpendicular a$[QQ']$, que es$m$. Por Axioma II,$m = (PP')$.