5.4: Reflexión a través de una línea
- Page ID
- 114817
Supongamos que\((AB)\) se dan el punto\(P\) y la línea. Para encontrar el reflejo\(P'\) de\(P\) lo ancho\((AB)\), uno deja caer una perpendicular desde\(P\) hacia\((AB)\), y la continúa a la misma distancia en el otro lado.
Según el Teorema 5.3.1,\(P'\) está determinado de manera única por\(P\).
Tenga en cuenta que\(P = P'\) si y solo si\(P \in (AB)\).
Asumir\(P'\) es un reflejo del punto\(P\) a través\((AB)\). Entonces\(AP' = AP\) y si\(A \ne P\), entonces\(\measuredangle BAP' \equiv -\measuredangle BAP\).
- Prueba
-
Tenga en cuenta que si\(P \in (AB)\), entonces\(P = P'\). Por Corolario 2.4.1,\(\measuredangle BAP = 0\) o\(\pi\). De ahí sigue el enunciado.
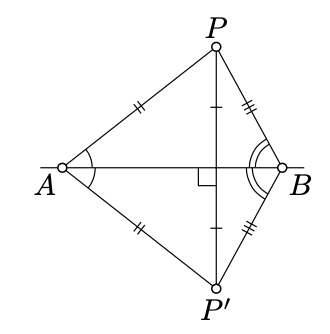
Si\(P \not\in (AB)\), entonces\(P' \ne P\). Por la construcción de\(P'\), la línea\((AB)\) es una bisectriz perpendicular de\([PP']\). Por lo tanto, según el Teorema 5.3.1,\(AP' = AP\) y\(BP' = BP\). En particular,\(\triangle ABP' \cong \triangle ABP\). Por lo tanto,\(\measuredangle BAP' = \pm \measuredangle BAP\).
Desde\(P' \ne P\) y\(AP' = AP\), lo conseguimos\(\measuredangle BAP' \ne \measuredangle BAP\). Es decir, nos dejan con el caso
\(\measuredangle BAP' = -\measuredangle BAP.\)
El reflejo a través de una línea es un movimiento del plano. Además, si\(\triangle P'Q'R'\) es el reflejo de\(\triangle PQR\), entonces
\(\measuredangle Q'P'R' \equiv \measuredangle QPR.\)
- Prueba
-
Tenga en cuenta que la composición de dos reflexiones a través de la misma línea es el mapa de identidad. En particular, cualquier reflexión es una biyección.
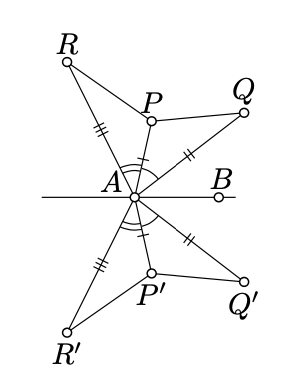
Fijar una línea\((AB)\) y dos puntos\(P\) y\(Q\); denotar sus reflejos a través\((AB)\) de\(P'\) y\(Q'\). Demostremos que
\[P'Q' = PQ;\]
es decir, la reflexión es conservadora de distancia, sin pérdida de generalidad, podemos suponer que los puntos\(P\) y\(Q\) son distintos de\(A\) y\(B\). Por Proposición\(\PageIndex{1}\), lo conseguimos
\(\begin{array} {rcl} {\measuredangle BAP'} & \equiv & {-\measuredangle BAP,} \\ {AP'} & = & {AP,} \end{array}\)\(\begin{array} {rcl} {\measuredangle BAQ'} & \equiv & {-\measuredangle BAQ,} \\ {AQ'} & = & {AQ.} \end{array}\)
De ello se deduce que
\[\measuredangle P'AQ' \equiv - \measuredangle PAQ.\]
Por SAS,\(\triangle P'AQ' \cong \triangle PAQ\) y sigue 5.4.1. Además, también conseguimos que
\(\measuredangle AP'Q' \equiv \pm \measuredangle APQ.\)
A partir de 5.4.2 y el teorema sobre los signos de ángulos de triángulos (Teorema 3.3.1) obtenemos
\[\measuredangle AP'Q' \equiv - \measuredangle APQ.\]
Repitiendo el mismo argumento para un par de puntos\(P\) y\(R\), obtenemos que
\[\measuredangle AP'R' \equiv -\measuredangle APR.\]
Restar 5.4.4 de 5.4.3, obtenemos eso
\(\measuredangle Q'P'R' \equiv -\measuredangle QPR.\)
Mostrar que cualquier movimiento del plano puede presentarse como una composición de como máximo tres reflexiones a través de líneas.
- Pista
-
Elija un triángulo arbitrario no degenerado\(ABC\). Supongamos que\(\triangle \hat{A} \hat{B} \hat{C}\) denota su imagen después del movimiento.
Si\(A \ne \hat{A}\), aplicar la reflexión a través de la bisectriz perpendicular de\([A\hat{A}]\). Esta reflexión envía\(A\) a\(\hat{A}\). Dejar\(B'\) y\(C'\) denotar las reflexiones de\(B\) y\(C\) respectivamente.
Si\(B \ne \hat{B}\), aplicar la reflexión a través de la bisectriz perpendicular de\([B'\hat{B}]\). Esta reflexión envía\(B'\) a\(\hat{B}\). Tenga en cuenta que\(\hat{A} \hat{B} = \hat{A} B'\); es decir,\(\hat{A}\) yace sobre la bisectriz perpendicular. Por lo tanto,\(\hat{A}\) se refleja a sí mismo. Supongamos que\(C''\) denota el reflejo de\(C'\).
Por último, si\(C'' \ne \hat{C}\), aplicar la reflexión a través\((\hat{A}\hat{B})\). Tenga en cuenta que\(\hat{A}\hat{C} = \hat{A} C''\) y\(\hat{B}\hat{C} = \hat{B} C''\); es decir,\((AB)\) es la bisectriz perpendicular de\([C''\hat{C}]\). Por lo tanto, esta reflexión envía\(C''\) a\(\hat{C}\).
Aplicar el Ejercicio 4.4.3 para mostrar que la composición de las reflexiones construidas coincide con el movimiento dado.
Los movimientos de plan se pueden dividir en dos tipos, directos e indirectos. El movimiento\(f\) es directo si
\(\measuredangle Q'P'R' = \measuredangle QPR\)
para cualquiera\(\triangle PQR\) y\(P' = f(P)\),\(Q' = f(Q)\) y\(R' = f(R)\); si en cambio tenemos
\(\measuredangle Q'P'R' \equiv -\measuredangle QPR\)
para cualquiera\(\triangle PQR\), entonces el movimiento\(f\) se llama indirecto.
En efecto, por Corolario\(\PageIndex{1}\), cualquier reflexión es un movimiento indirecto. Aplicando el ejercicio anterior, cualquier movimiento es una composición de reflexiones. Si el número de reflexiones es impar entonces la composición indirecta; si el número es par, entonces el movimiento es directo.
Dejar\(X\) y\(Y\) ser los reflejos de\(P\) a través de las líneas\((AB)\) y\((BC)\) respectivamente. Demostrar que
\(\measuredangle XBY \equiv 2 \cdot \measuredangle ABC.\)
- Responder
-
Tenga en cuenta que\(\measuredangle XBA = \measuredangle ABP, \measuredangle PBC = \measuredangle CBY\). Por lo tanto,
\(\measuredangle XBY \equiv \measuredangle XBP + \measuredangle PBY \equiv 2 \cdot (\measuredangle ABP + \measuredangle PBC) \equiv 2 \cdot \measuredangle ABC.\)


